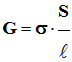|
antiseptique : |
La solution aqueuse de permanganate de potassium |
|
|
|
|
-
Le permanganate de potassium, ou
cristal de Condy, est un composé ionique de formule
KMnO4 (s).
-
Dissous dans l’eau, il forme une
solution aqueuse violette d’ions potassium
K+ (aq) et d’ions
permanganate MnO4–
(aq).
-
La solution aqueuse est utilisée à
des concentrations différentes comme :
-
Antiseptique cutané,
-
Désinfectant pour laver les
légumes,
-
Ou pour le nettoyage des aquariums
en aquariophilie.
II-
Document 01 : Un sachet de cristal de Condy :
-
Conditionnement :
-
Sachet de 0,25 g de
KMnO4 (s) en poudre.
-
Masse molaire du permanganate de
potassium solide : M = 158,0 g . mol–1.
-
Présentation : le sachet :

-
La poudre de permanganate de
potassium :

-
Une solution aqueuse de
permanganate de potassium :

-
La solution aqueuse obtenue est de
couleur violette.
-
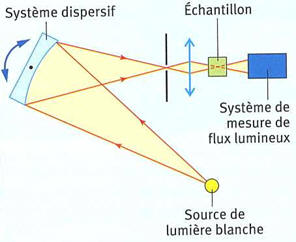
Spectre d’absorption d’une
solution aqueuse de permanganate de potassium :
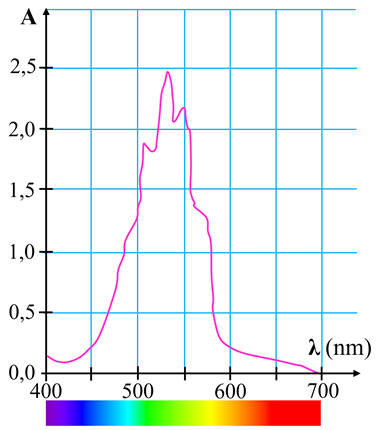
-
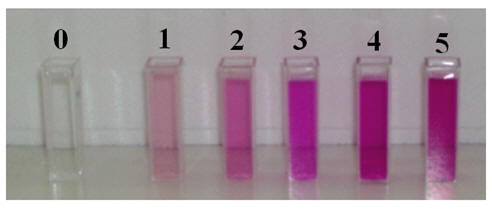
Échelle des teintes :
https://physiquechimielycee.com/scphysiques2010/tsqcm/tsqcm01chim.htm
|
|
|||||
|
Solution N° 0
Eau distillée |
Solution N° 1
C1
= 1,0 ×
10–
4
mol /L |
Solution N° 2
C2
= 2,0 ×
10
– 4
mol /L |
Solution N° 3
C3
= 3,0 ×
10
– 4
mol /L |
Solution N° 4
C4
= 4,0 ×
10
– 4
mol /L |
Solution N° 5
C5
= 5,0 ×
10
– 4
mol /L |
- La solution est d’autant plus
violette qu’elle est concentrée.
-
Utilisation :
- Dissoudre dans l’eau distillée le
contenu du sachet dans :
- 0,60 L pour désinfecter des fruits
et des légumes ;
- 1,0 L pour un usage antiseptique
cutané ;
- 2,0 L pour éliminer les algues,
bactéries et champignons sur les parois d’un aquarium ; ajouter ensuite 20 mL de
la solution préparée par litre d’eau de l’aquarium.
III-
Document 02 : Conductance et
conductivité.
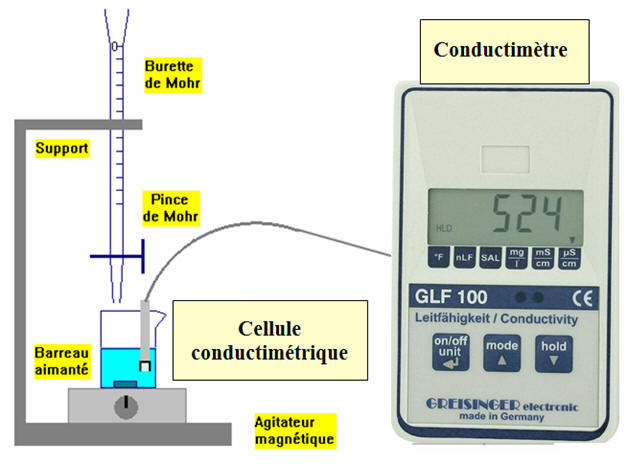
1)- Le conductimètre :
https://physiquechimielycee.com/scphysiques2010/tsch18.htm
| Le conductimètre est constitué : - D'une sonde de conductimétrie (deux plaques conductrices en vis-à-vis, alimentées par une tension alternative. - D'un boîtier qui sert d'alimentation pour la sonde. - Ce boîtier dispose en outre d'une zone de lecture, d'un bouton de réglage de la température et d'un bouton d'étalonnage. - Un troisième bouton permet en général de sélectionner le calibre. |
- Montage : Titrage conductimétrique
2)- Conductance et
conductivité.
- Un conductimètre mesure la
conductance G de la portion de
solution comprise entre les plaques de mesure.
- L’unité de conductance
G est le siemens (S), c’est
l’inverse de la résistance R qui
s’exprime en ohm (Ω).
- Après étalonnage, , le
conductimètre mesure la conductivité σ
de la solution.
- La conductance G d’une
portion de solution est proportionnelle au rapport
![]() (grandeurs caractéristiques
de la cellule).
(grandeurs caractéristiques
de la cellule).
- Par définition, le coefficient de
proportionnalité est appelé : conductivité de la solution ionique que l’on note
σ
‘’sigma minuscule’’.
- Relation :
|
|
G :
conductance en siemens S |
|
S :
surface des électrodes en m2. |
|
|
ℓ :
distance entre les électrodes en m. |
|
|
σ :
conductivité de la solution en S . m– 1 |
-
La grandeur σ est
caractéristique de la solution.
- Elle dépend de la nature et de la
concentration des ions dissous dans la solution
- Elle s’exprime en siemens par
mètre (S . m– 1) dans le
S.I.
-
La conductivité
σ de la
solution est égale à la somme des conductivités due aux cations et aux anions.
- On écrit :
-
σ = σ
(+) + σ
(–)
- Formule générale :
https://physiquechimielycee.com/scphysiques2010/tsch18.htm
- 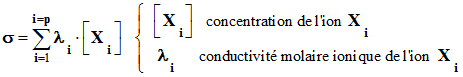
-
Conductivité molaire ionique :
- λ (MnO4–)
= 6,13 mS .m2 . mol–1
- λ (K+)
= 7,35 mS .m2 . mol–1
IV-
Document 03 : Absorbance d’une solution aqueuse.
- On utilise le fait que toute
solution colorée absorbe la lumière visible (400 nm < λ0 < 800
nm)
- Lorsqu’un faisceau de lumière
monochromatique traverse un milieu absorbant, l’intensité lumineuse I du
faisceau transmis est inférieure à l’intensité lumineuse I0 du
faisceau incident.
- Pour évaluer cette diminution, on utilise :
- La transmittance T : T
= I /
I0
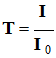
- L’absorbance A :
- 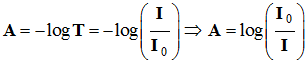
- La transmittance
T s’exprime en pourcentage.
- À une transmittance T de
100 % (T = 1) correspond une absorbance nulle : A = 0.
- à
une transmittance de 1 % (T = 0,01) correspond une absorbance A =
log 100 = 2.
- L’absorbance est une grandeur sans
unité.

- Une solution a été préparée dans
un flacon non étiqueté.
- Comment vérifier, à l’aide de deux
stratégies d’analyses physiques différentes, pour quel usage cette solution a
été préparée ?
-
Réponse 01 :
-
On peut déterminer la
concentration de la solution préparée par :
- spectrophotométrie
- conductimétrie
- À partir de la connaissance de la
concentration, peut en déduire son usage :
-
Identifier deux méthodes physiques
envisageables pour déterminer la concentration en quantité d’ion permanganate et
d’ion potassium dans la solution inconnue.
- La solution à étudier étant trop
concentrée, elle sera diluée dix fois avant analyse.
- Élaborer une démarche
expérimentale détaillée permettant de répondre à la question posée.
4)- Question 04 :
mettre en œuvre la démarche proposée
- Comparer les deux méthodes
expérimentales mises en œuvre.
- Une solution a été préparée dans
un flacon non étiqueté.
- Comment vérifier, à l’aide de deux
stratégies d’analyses physiques différentes, pour quel usage cette solution a
été préparée ?
- On peut déterminer la
concentration de la solution préparée par :
- Spectrophotométrie ou
- Conductimétrie.
- À partir de la connaissance de la
concentration, on peut en déduire son usage.
- Solution 01 : Solution pour désinfecter
des fruits et des légumes :
- Masse de permanganate de potassium
solide :
- m1 =
0,25 g
-
Volume de la solution :
- V1 =
0,60 L
- Masse molaire du permanganate de
potassium solide : M = 158,0 g . mol–1.
-
Équation de la réaction de
dissolution :
|
|
|
Eau |
|
|
|
|
KMnO4
(s) |
→ |
MnO4–
(aq) |
+ K+
(aq) |
|
Initial |
n |
|
0 |
0 |
|
Final |
0 |
|
n |
n |
|
Concentration
|
C1
= n1
/ V1 |
|
C1
= n1
/ V1 |
C1
= n1
/ V1 |
- Les différentes concentrations :
- C (KMnO4)
= [MnO4–] = [K+]
= C1
- Concentration molaire volumique de
la solution S1 :
- 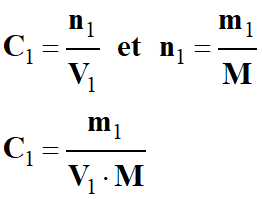
- Applications numériques :
Détermination des concentrations des différentes solutions.
- Détermination de
C1 :
- 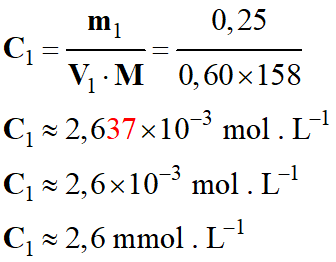
- Détermination de
C2 concentration de la
solution S2 :
- 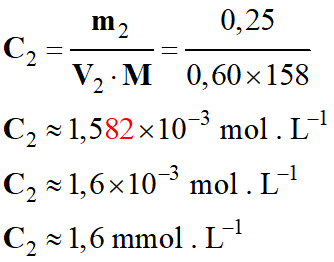
- Détermination de
C3 concentration de la
solution S3 :
- 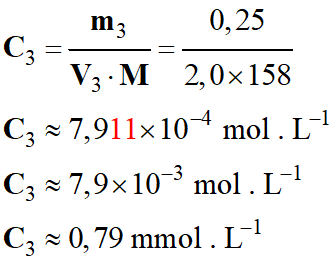
- Tableau des concentrations des
différentes solutions :
|
|
Type de
solution |
Concentration
molaire
mol . L–1 |
|
S1
(1 sachet et
0,60 L) |
Désinfecter
des fruits
et des
légumes |
2,6 × 10–3 |
|
S2
(1 sachet et
1,0 L) |
Antiseptique
cutané |
1,6 × 10–3 |
|
S2
(1 sachet et
2,0 L) |
Nettoyage des
aquariums |
7,9 × 10–4 |
- Identifier deux méthodes physiques
envisageables pour déterminer la concentration en quantité d’ion permanganate et
d’ion potassium dans la solution inconnue.
![]() Méthode spectrophotométrique :
Méthode spectrophotométrique :
- Principe :
- Pour déterminer la
concentration d’une solution de permanganate de potassium à l’aide d’un
spectrophotomètre, il faut mesurer l’absorbance de la solution à une longueur
d’onde donnée.
- La relation entre
l’absorbance et la concentration est donnée par la loi de Beer-Lambert.
- La loi de Beer-Lambert
énonce que l’absorbance A est proportionnelle à la concentration C
de la solution et à la longueur ℓ du trajet optique traversé par la
lumière.
|
L’absorbance
d’une solution diluée contenant une espèce colorée est
proportionnelle à la concentration (effective)
C de cette espèce et à
l’épaisseur ℓ (cm) de la solution traversée par le faisceau
lumineux. |
|
A
(λ) =
ε (λ)
. ℓ .
C |
|
A :
absorbance : grandeur sans unité |
|
ℓ :
largeur de la cuve (épaisseur de la solution traversée) (cm) |
|
ε
(λ) : coefficient
d’extinction molaire (mol– 1. L. cm– 1) |
|
C :
concentration de l’espèce absorbante (mol
. L– 1) |
- Pour déterminer la
concentration de la solution, il suffit de mesurer l’absorbance de la solution à
la longueur d’onde donnée et de calculer la concentration à l’aide de la loi de
Beer-Lambert.
- D’autre part :
- La courbe A
= f (C) constitue la courbe d’étalonnage de la substance étudiée.
- Elle permet de
déterminer la concentration d’une solution de la substance étudiée.
- Elle permet donc
de doser une espèce chimique colorée.
- Afin d’augmenter
la sensibilité de la méthode, on utilise la longueur d’onde qui correspond au
maximum d’absorption de la substance étudiée.
- Cette méthode est
alors beaucoup plus précise que la méthode colorimétrique utilisant une échelle
des teintes.
- Remarque : la
solution colorée doit être suffisamment diluée,
- C
≤ 1,0 × 10–2 mol . L–1, et le spectrophotomètre ne doit
pas saturer.
- Le choix de la longueur d’onde :
- Pour déterminer la concentration
d’une solution de permanganate de potassium à l’aide d’un conductimètre, il faut
mesurer la conductivité de la solution.
- La relation entre la conductivité
et la concentration est donnée par la loi de Kohlrausch.
- Énoncé de la loi de Kohlrausch :
|
La
conductivité σ d’une
solution diluée d’une espèce ionique dissoute
est proportionnelle à sa concentration molaire C en soluté
apporté : |
|
σ
= k .
C |
|
C ;
concentration en mol . L– 1 |
|
k :
coefficient de proportionnalité en S . L .
m– 1. mol– 1 |
|
σ :
conductivité de la solution en S . m– 1 |
- Pour déterminer la concentration
de la solution, il suffit de mesurer la conductivité de la solution à l’aide
d’un conductimètre et de calculer la concentration à l’aide de la loi de
Kohlrausch.
-
Remarque :
- On peut le faire
aussi à partir de la valeur de la conductance si on ne possède pas de
conductimètre.
![]() Remarque :
Remarque :
- Les lois de
Beer-Lambert
et
Kohlrausch
ont des équations analogues.
- La solution colorée doit être
suffisamment diluée, C ≤ 1,0 × 10–2 mol . L–1, et
ne doit contenir qu’un seul soluté ionique.
- La solution à étudier étant trop
concentrée, elle sera diluée dix fois avant analyse.
- Élaborer une démarche
expérimentale détaillée permettant de répondre à la question posée.
![]() Dilution d’une solution :
Dilution d’une solution :
- On doit effectuer une dilution car
la concentration molaire du soluté diminue.
- Lors d’une dilution, la
concentration molaire du soluté diminue, mais sa quantité de matière ne change
pas.
-
On dit qu’au cours d’une dilution,
la quantité de matière de soluté se conserve.
- La solution de départ est appelée
la solution mère et la solution diluée est appelée la solution fille.
|
S1
Solution mère |
C1
= V1
= ? n1 =
C1 . V1 |
Dilution
→ |
S2
Solution fille |
C’1
= C1 / 10 V’1
= 100 mL n’1 =
C’1 . V’1 |
|
Si
A représente l’espèce présente dans la solution. La quantité
de matière nA de cette espèce est la
même dans la solution mère et dans la solution fille. - Il
y a conservation de la quantité de matière de soluté :
- la
quantité de matière de soluté présente dans la solution mère : n1 = C1
. V1 (1) - la
quantité de matière de soluté présente dans la solution fille :
n’1 = C’1 . V’1
(2) - Conséquence :
C1 . V1 = C’1
. V’1 avec obligatoirement V1 < V’1. |
![]() Calcul du volume de la solution
mère à prélever :
Calcul du volume de la solution
mère à prélever :
- Comme la solution mère est trop
concentré, on va la diluer 10 fois.
- C’1
= C1 / 10
- On veut préparer un volume V’1
= 100 mL d solution fille.
- n1 =
n’1 => C1
. V1 = C’1
. V’1
- 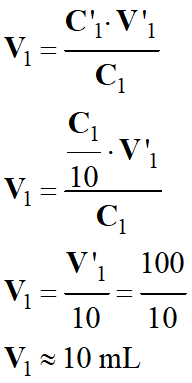
![]() Préparation de la solution fille :
Préparation de la solution fille :
|
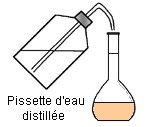
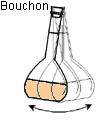
On verse
suffisamment de solution mère dans un bécher On ne pipette jamais
dans le récipient qui contient la solution mère On prélève
le volume V = 10,0 mL à
l’aide d’une pipette jaugée muni de sa propipette. On verse le
volume V = 10,0 mL dans une
fiole jaugée de 100,0 mL. On remplit
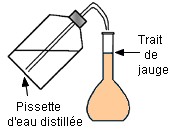
la fiole jaugée environ aux trois quarts avec de l’eau. On complète
avec de l’eau distillée jusqu’au trait de jauge. On ajuste
le niveau avec une pipette simple. On bouche
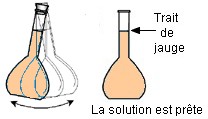
et on agite pour homogénéiser. La solution
est prête. |
|
Verser suffisamment de solution Mère dans un bécher |
Deuxième étape : On prélève le volume nécessaire de solution Mère à l’aide d’une pipette jaugée munie de sa propipette |
Troisième étape : On verse le volume nécessaire de solution dans la fiole jaugée de volume approprié.. |
|
On ne pipette jamais directement dans le flacon qui contient
la solution
Mère |
|
|
|
Quatrième étape : On ajoute de l’eau distillée et on agite mélanger et homogénéiser |
Cinquième étape : On complète avec une pissette d’eau distillée jusqu’au trait de jauge. |
Sixième étape : on agite pour homogénéiser. La solution est prête. |
|
|
|
|
- Concentration des différentes
solutions :
|
|
Solution mère |
Solution fille |
|
|
Concentration
molaire
mol . L–1 |
Concentration
molaire
mmol . L–1 |
|
S1
(1 sachet et
0,60 L) |
2,6 × 10–3 |
0,26 |
|
S2
(1 sachet et
1,0 L) |
1,6 × 10–3 |
0,16 |
|
S2
(1 sachet et
2,0 L) |
7,9 × 10–4 |
0,079 |
VII- Mise
en œuvre de la démarche proposée.
1)- Méthode
spectrophotométrique.
a)-
Réglage du spectrophotomètre.
- Pour réaliser les mesures d’absorbance, le spectrophotomètre est
généralement réglé sur la longueur d’onde
λmax
correspondant au maximum d’absorption du spectre de la solution étudiée.
- À cette longueur
d’onde, la valeur de l’absorbance étant la plus grande, l’incertitude sur la
mesure est la plus petite.
-
Choix de la
longueur d’onde :
- Exploitation de la courbe
A =
f (λ)
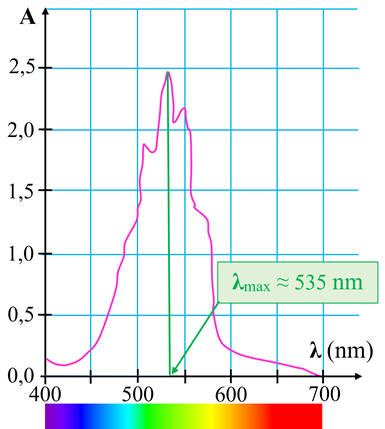
- Pour les solutions aqueuses de permanganate de potassium, on
choisit λ = 535 nm, pour avoir le maximum de variations pour la valeur de
A.
b)-
Préparation des solutions et
mesures :
- Les solutions diluées à mesurer ont des concentrations comprises
entre 0,070 mmol . L–1 et 0.30 mmol . L–1.
- On dispose d’une
solution S0 de concentration en permanganate de potassium C0
= 0,50 mmol / L.
- À partir de S0,
préparer les solutions 10 mL de solution S en utilisant les solutions
présentes dans les burettes.
- Pour préparer la
solution S, on mélange la solution de permanganate de potassium de
concentration C0 = 0,50 mmol / L et on complète avec de l’eau
distillée.
- Pour préparer la
solution 1, on mélange à l’aide des burettes graduées, 1,0 mL de solution
de permanganate de potassium de concentration C0 = 0,50 mmol /
L et 9 mL d’eau distillée.
-
Pour préparer la
solution 2, on mélange à l’aide des burettes graduées, 2 mL de solution
de permanganate de potassium de concentration C0 = 1,0 mmol /
L et 8 mL d’eau distillée.
- Ainsi de suite….
|
Groupe |
C mmol . L–1 |
A |
|
1 |
0,050 |
0,101 |
|
2 |
0,10 |
0,203 |
|
3 |
0,15 |
0,302 |
|
4 |
0,20 |
0,405 |
|
5 |
0,25 |
0,503 |
|
6 |
0,30 |
0,607 |
|
7 |
0,35 |
0,704 |
|
8 |
0,40 |
0,805 |
|
9 |
0,45 |
0,908 |
|
10 |
0,50 |
1,030 |
- On trace la courbe A = f (C).
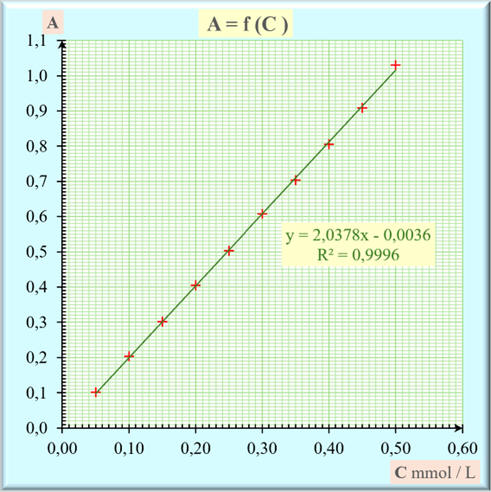
- On obtient la
courbe d’étalonnage.
- Ce graphe est une
portion de droite passant par l’origine.
- L’absorbance A
est proportionnelle à la concentration C de la solution aqueuse de
permanganate de potassium.
- La loi de Beer-Lambert est
vérifiée tant que les solutions sont suffisamment diluées.
- Dans le domaine des concentrations
utilisées,
- Le modèle traduit bien les
variations de l’absorbance en fonction de la concentration.
- On peut en déduire que :
- A
= k . [MnO4–].
- Relation mathématique :
- y ≈ 2,0378
x – 0,0036 et le coefficient de
détermination : R2 = 0,9996
-
le coefficient de détermination
R2 est proche de 1.
- L’adéquation entre les deux
grandeurs est excellente.
- Relation mathématique arrondie :
- On peut en déduire que :
- y ≈ 2,04
x
- Traduction en physique et chimie :
- A
≈ 2,04 × [MnO4–] avec la concentration en
mmol . L–1
e)-
Concentration en quantité d’ion
permanganate et d’ion potassium dans la solution inconnue :
-
Mesure de l’absorbance
A de la solution à identifier :
- A = 0,349
-
La concentration de cette solution
peut être déterminée par lecture graphique ou à l’aide de l’équation de la
courbe d’étalonnage.
-
Lecture graphique :

- [MnO4–]
=
C
≈ 0,17 mmol . L–1
- À partir de l’équation :
- [MnO4–]
=
C =
2,04 / 349 mmol . L–1
-
[MnO4–]
=
C
≈ 0,171 mmol . L–1
|
|
Solution mère |
Solution fille |
|
|
Concentration molaire
mol . L–1 |
Concentration molaire
mmol . L–1 |
|
S2
(1 sachet et
1,0 L) |
1,6 × 10–3 |
0,16 |
-
La solution étudiée est la
solution S2 :
Antiseptique cutané.
- Remarque : le fait de réaliser
plusieurs mesures permet d’obtenir une plus grande précision.
2)- Méthode
conductimétrique :
- Régler le bouton
de température du conductimètre sur la température de la pièce.
- Rincer (avec de
l'eau distillée) et essuyer délicatement (avec du papier Joseph) la sonde.
- Plonger la sonde
dans une solution d'étalonnage.
- Régler le bouton
d'étalonnage du conductimètre pour que la valeur affichée coïncide avec la
valeur donnée par le fabriquant de la solution d'étalonnage (à la température de
la pièce).
- Sortir la sonde de la solution d'étalonnage, la rincer, la
replacer dans l'eau distillée.
- Rincer la sonde de
conductimétrie (si possible avec la solution dont on veut mesurer la
conductivité).
- L'essuyer
délicatement avec du papier Joseph.
-
Plonger la sonde
dans la solution dont on veut mesurer la conductivité.
- Attendre la
stabilité (quelques secondes).
- Lorsque la lecture est terminée, rincer la sonde et la plonger
dans la solution d'eau.
d)-
Préparation des solutions et
mesures :
- Les solutions diluées à mesurer ont des concentrations comprises
entre 0,070 mmol . L–1 et 0.30 mmol . L–1.
- On dispose d’une
solution S0 de concentration en permanganate de potassium C0
= 0,50 mmol / L.
- À partir de S0,
préparer les solutions 10 mL de solution S en utilisant les solutions
présentes dans les burettes.
- Pour préparer la
solution S, on mélange la solution de permanganate de potassium de
concentration C0 = 0,50 mmol / L et on complète avec de l’eau
distillée.
- Pour préparer la
solution 1, on mélange à l’aide des burettes graduées, 1,0 mL de solution
de permanganate de potassium de concentration C0 = 0,50 mmol /
L et 9 mL d’eau distillée.
-
Pour préparer la
solution 2, on mélange à l’aide des burettes graduées, 2 mL de solution
de permanganate de potassium de concentration C0 = 1,0 mmol /
L et 8 mL d’eau distillée.
- Ainsi de suite….
|
Groupe |
C mmol . L–1 |
σ μS . cm–1 |
|
1 |
0,050 |
5,17 |
|
2 |
0,10 |
10,60 |
|
3 |
0,15 |
16,43 |
|
4 |
0,20 |
20,69 |
|
5 |
0,25 |
25,89 |
|
6 |
0,30 |
31,04 |
|
7 |
0,35 |
36,21 |
|
8 |
0,40 |
41,41 |
|
9 |
0,45 |
46,56 |
|
10 |
0,50 |
51,74 |
f)-
Exploitation des mesures :
- Courbe :
σ =
f (C)

- Ce graphe est une
portion de droite passant par l’origine.
- La conductivité de
la solution est proportionnelle à la concentration C de la solution
aqueuse de permanganate de potassium.
-
La loi
de Kohlrausch est vérifiée tant
que les solutions sont suffisamment diluées.
- Dans le domaine des concentrations
utilisées,
- Le modèle traduit bien les
variations de la conductivité en fonction de la concentration.
- On peut en déduire que :
- σ
= k
. C
- Relation mathématique :
- y ≈ 102,72
x – 0,3253 et le coefficient de
détermination : R2 = 0,9997
-
Le coefficient de détermination
R2 est proche de 1.
- L’adéquation entre les deux
grandeurs est excellente.
-
Relation mathématique arrondie :
- On peut en déduire que :
- y ≈ 102,7
x
- Traduction en physique et chimie :
-
σ
(μS . cm–1)≈
102,7 ×
C
(mmol . L–1)
g)-
Concentration d’ion
permanganate et d’ion potassium dans la solution inconnue.
- Mesure de la conductivité de la
solution à identifier :
- σ = 17,61 μS . cm–1
- La concentration de cette solution
peut être déterminée par lecture graphique ou à l’aide de l’équation de la
courbe d’étalonnage.
- Lecture graphique :
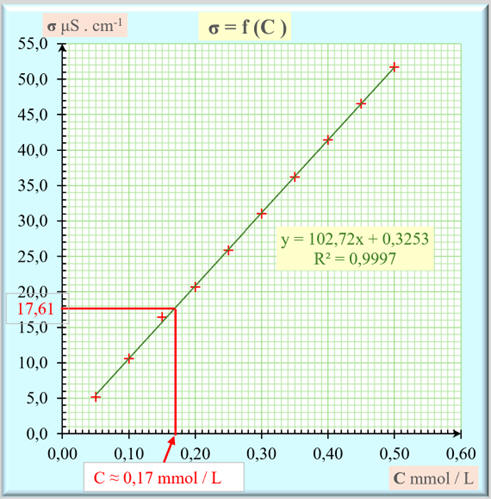
- C
≈ 0,17 mmol . L–1
- À partir de l’équation :
- C =
17,61 / 102,7 mmol .
L–1
- C ≈
0,1714 mmol . L–1
- C ≈
0,17 mmol . L–1
|
|
Solution mère |
Solution fille |
|
|
Concentration molaire
mol . L–1 |
Concentration
molaire
mmol . L–1 |
|
S2
(1 sachet et
1,0 L) |
1,6 × 10–3 |
0,16 |
- La solution étudiée est la
solution S2 :
Antiseptique cutané.
- Quelques liens :
- On peut réaliser la manipulation
sans conductimètre :
TP Chimie N°06 Concentration et conductimétrie
TP Chimie N° 08 Titrage conductimétrique
VIII-
Solution de permanganate de potassium et oxydoréduction :
TP Chimie N° 13 Oxydation ménagée des alcools :
Le couple MnO4– (aq) / Mn2+ (aq) :
TP Chimie N° 09 Synthèse de l’acide benzoïque :
TP Chimie N° 10 Titrage colorimétrique :
Synthèse d’une cétone : La propan-2-one :
TP Chimie N° 08 Synthèse d’une cétone : La propan-2-one :
Établir une demi-équation électronique : couple MnO4– (aq) / Mn2+ (aq)
1)-
Oxydation et ion permanganate.
-
Pour rappel :
-
L’oxydation est une réaction
chimique au cours de laquelle une espèce chimique perd des électrons.
-
L’ion permanganate, MnO4-
(aq), est un oxydant.
-
Il peut capter des électrons et se
réduire en une autre espèce chimique.
-
Quelques couples oxydant /
réducteur avec l’élément manganèse :
-
Couple 1 :
-
MnO4-
(aq) / MnO2 (s) E0 = 1,69 V
-
Demi-équation électronique :
-
MnO4-
(aq) + 4 H+ (aq) + 3 e-
![]() MnO2
(s) + 2 H2O (ℓ)
MnO2
(s) + 2 H2O (ℓ)
|
|
Demi-équation
électronique |
|
Première étape :
On écrit le couple
oxydant / réducteur |
MnO4– |
|
Deuxième étape : On équilibre l’élément oxygène
avec de l’eau |
MnO4–
(aq)
|
|
Troisième étape : On équilibre l’élément hydrogène avec H+ (on travaille
en milieu acide) |
MnO4–
(aq)
+
4
H+
|
|
Quatrième étape : On équilibre
les charges
avec les électrons. |
MnO4–
(aq)
+
4
H+
+ 3 e –
|
-
Couple 2 :
-
MnO4-
(aq) / Mn2+ (aq) E0
= 1,51 V;
-
Demi-équation électronique :
-
MnO4–
+ 8
H+
+ 5
e –
![]() Mn2+
+ 4
H2O
Mn2+
+ 4
H2O
-
Méthode pour retrouver cette demi-équation
électronique : la même que précédemment
|
|
Demi-équation
électronique |
|
Première étape :
On écrit le couple
oxydant / réducteur |
MnO4–
(aq)
|
|
Deuxième étape : On équilibre l’élément oxygène
avec de l’eau |
MnO4–
(aq)
|
|
Troisième étape : On équilibre l’élément hydrogène
avec H+ (on travaille
en milieu acide) |
MnO4–
(aq) +
8
H+
(aq)
|
|
Quatrième étape : On équilibre
les charges
avec les électrons. |
MnO4–
(aq) +
8
H+
(aq) +
5 e – |
-
Couple 3 :
-
MnO2 (s) / Mn2+ (aq) E0 = 1,23 V
-
Demi-équation
électronique :
-
MnO2
(s) + 4 H+ (aq) + 2 e-
![]() Mn2+ (aq) + 2 H2O (ℓ)
Mn2+ (aq) + 2 H2O (ℓ)
|
|
Demi-équation
électronique |
|
Première étape :
On écrit le couple
oxydant / réducteur |
MnO2 (s)
|
|
Deuxième étape : On équilibre l’élément oxygène
avec de l’eau |
MnO2 (s)
|
|
Troisième étape : On équilibre
l’élément hydrogène
avec H+ (on travaille
en milieu acide) |
MnO2 (s)
+
4
H+
|
|
Quatrième étape : On équilibre
les charges
avec les électrons. |
MnO2 (s)
+
4
H+
+ 2 e –
|
-
Couple
4 :
-
Mn3+ (aq) / Mn2+
(aq) E0 = 1,50 V
-
Demi-équation électronique :
-
Mn3+ (aq) + e-
= Mn2+ (aq)
-
Il existe d’autres couples Ox / Red où intervient
l’élément manganèse.
-
L’ion permanganate est un oxydant très puissant,
car il a un potentiel d’oxydoréduction élevé :
-
MnO4–
(aq) / MnO2 (s) E0 = 1,69 V ou MnO4–
(aq) / Mn2+ (aq) E0 = 1,51 V
-
Il peut
oxyder de nombreux réducteurs, comme le fer (II), le sulfite, l’iodure, etc.
2)-
Exemple : Réaction
entre l’ion permanganate et l’ion fer (II) en milieu acide.
-
Les couples qui interviennent :
-
MnO4–
(aq) / Mn2+ (aq) E0 = 1,51 V et Fe3+
(aq) /
Fe2+
(aq) E0 = 0,77 V
-
On peut utiliser la règle du gamma pour mettre en
évidence la réaction qui se produit entre les ions permanganate
MnO4-
(aq) en milieu acide et les ions fer II, Fe 2+ (aq).
-
Les réactifs mis en présences : MnO4–
(aq) et Fe 2+ (aq)
-
Classement des deux couples :
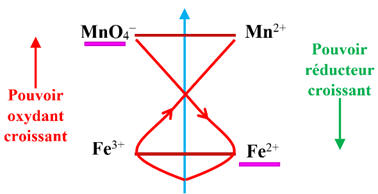
-
D’après la règle du gamma, il se produit la réaction
suivante :
-
L’oxydant le plus fort réagit sur le réducteur le plus fort présent dans le
mélange réactionnel.
-
Remarque :
-
On peut
aussi considérer le couple
Ox
/ Red
suivant : Fe2+ (aq) / Fe (s) E0
= - 0,45 V
-
Si on
place tous les couples pouvant intervenir, on remarque que différentes réactions
chimiques peuvent se produire.
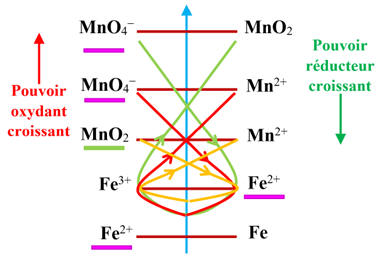
-
L’ion permanganate MnO4–
(aq) est un oxydant plus fort que l’ion fer II, Fe2+ (aq).

-
Titrage colorimétrique :
Détermination de la concentration des ions fer II d’une solution de sel de Mohr.
-
Lorsque l’on effectue le
dosage colorimétrique,
-
La solution de permanganate de potassium (K+(aq)
+ MnO4–
(aq)) acidifiée
-
se décolore presque immédiatement en présence de
sel de Mohr
(ions fer
II,
Fe2+
(aq)).
-
La solution dans le tube à essais prend une teinte orange caractéristique
des ions fer
III,
Fe3+
(aq).
-
Équation bilan de la réaction :
|
5
(
Fe2+
(aq)
|
|
1 ( MnO4– (aq)
+
8
H+
(aq) +
5 e
–
|
|
MnO4–
(aq)
+ 8
H+
(aq) +
5 Fe2+
(aq)
→
Mn2+
(aq) +
5
Fe3+
(aq)
+
4
H2O
(ℓ)
|
3)-
Géométrie de l’ion permanganate
Vers les entités chimiques stables.
-
Les gaz nobles
(hélium,
He,
néon,
Ne, argon,
Ar, …) possèdent une
stabilité énergétique remarquable.
-
Ils réagissent très
rarement avec d’autres éléments.
-
Leur configuration
électronique de valence est de la forme ns2
np6.
-
Ou dans le cas de
l’hélium, 1s2.
-
La valence d’un atome est égale au
nombre d’électrons de valence de cet atome.
-
Pour Z ≤ 18, les électrons
de valence sont ceux qui occupent la couche électronique de nombre n le
plus élevé.
-
Cette dernière est appelée couche
électronique de valence, sa configuration électronique se nomme configuration
électronique de valence.
-
L’atome de manganèse :
Z = 25 (le manganèse fait partie des éléments de transition).
-
Configuration électronique de l’atome de manganèse :
1s2
2s2
2p6 3s2 3p6
4s2 3d5
-
Configuration électronique de l’argon Ar :
1s2
2s2
2p6
3s2
3p6
-
Notation simplifiée : [Ar]
4s2
3d5
-
Couche électronique de valence ;
4s2
3d5
-
L’atome de manganèse
possède 7 électrons de valence.
-
L’atome d’oxygène : Z
= 8
-
Configuration électronique de l’atome d’oxygène :
1s2
2s2 2p4
-
Notation simplifiée : [He]
2s2
2p4
-
Couche électronique de valence ;
2s2
2p4
-
L’atome d’oxygène possède 6 électrons de valence.
c)-
L’atome de manganèse est-il hypervalent ?
-
L’atome de manganèse n’est pas
hypervalent.
-
Un atome est dit hypervalent
lorsqu’il forme plus de liaisons que ce que sa valence naturelle le permet.
d)-
Schéma de Lewis de l’ion permanganate.
-
Le schéma de Lewis de
l’ion permanganate MnO4– est une représentation
simplifiée de la structure électronique de cet ion.
-
Il montre les atomes, les
liaisons covalentes et les doublets non liants de l’ion.
-
Étape 01 :
-
On détermine le nombre
d’électrons de valence de l’ion.
-
Nombre total
d'électrons de valence (Nv)
-
Tableau :
|
MnO4– |
|
Nombre
d’atomes |
Total
|
Total
général |
|
Manganèse : Mn |
7 e– |
7 |
7 |
Nv
= 31 + 1
Nv
= 32 |
|
Oxygène : O |
6 e– |
4 |
24 |
|
|
Charge portée
|
– e |
gain |
1 |
-
L’ion permanganate porte
une charge négative – e, ce qui signifie qu’il possède un électron
supplémentaire.
-
Étape 02 :
-
On place l’atome de
manganèse au centre et les atomes d’oxygène autour, en les reliant par des
liaisons simples.
-
Première représentation :
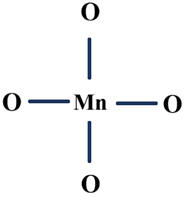
-
Chaque liaison simple
représente deux électrons partagés.
-
Nombre d’électrons restant
à placer : 32 - 4 × 2 = 24
-
Étape 3 :
-
On complète les octets des
atomes périphériques (les atomes d’oxygène) en plaçant des doublets non liants
autour d’eux.
-
Octet complété :

-
Nombre total d’électrons : N = 16
× 2 = 32
-
Le nombre
d’électrons est en accord avec la valeur de Nv = 32
-
Charge formelle portée
par chaque atome d’oxygène :
-
Cf
(Oa) = 6 – (4 + 2)
-
Cf
(Oa) = 0
-
Cf
(Ob)
= 6 – (4 + 2)
-
Cf
(Ob)
= 0
-
Cf
(Oc)
= 6 – (4 + 2)
-
Cf
(Oc)
= 0
-
Cf
(Od)
= 6 – (6 + 1)
-
Cf
(Od)
= – 1
- Cet atome d’oxygène porte une charge formelle négative ![]()
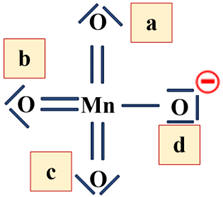
-
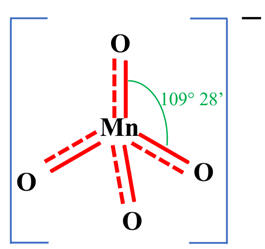
Géométrie de l’ion
permanganate :
-
La géométrie de l’ion
permanganate (MnO4–) est tétraédrique.
-
L’atome de manganèse est
situé au centre d’un tétraèdre régulier dont les atomes d’oxygène occupent les
sommets.
-
Les angles sont de 109,5
°.
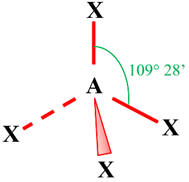
- Méthode VSEPR :
|
Type de molécule |
AX4 |
|
Nombre de paires liantes d’électrons |
4 |
|
Géométrie de la molécule |
Atome central tétragonal
Molécule tétraédrique |
Géométrie de l'ion permaganate :