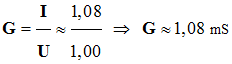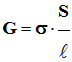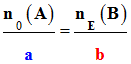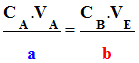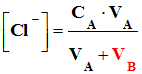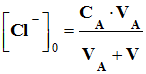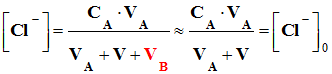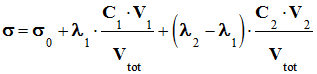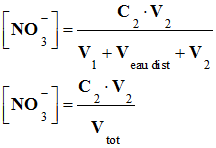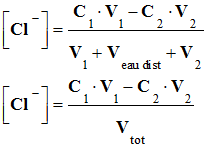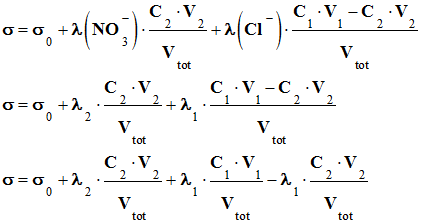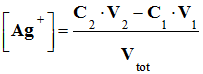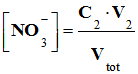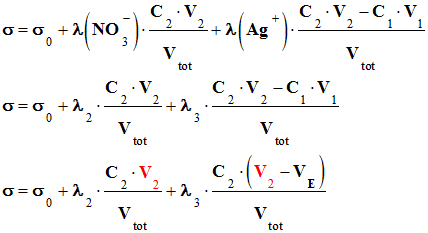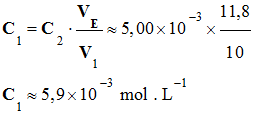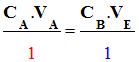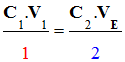|
Chap. N° 18 |
Contrôle de qualité par dosage. Cours. |
|
|
|
|
En travaux a)- Exercice 6 page 478 : Utiliser la loi de Beer-Lambert.b)- Exercice 7 page 478 : Utiliser la loi de Kohlrausch.c)- Exercice 8 page 478 : Utiliser une relation d’équivalence.d)- Exercice 14 page 480 : Choisir un indicateur coloré.e)- Exercice 16 page 481 : Titrage colorimétrique d’une eau oxygénée.f)- Exercice 18 page 481 : Retrouver la loi de Kohlrausch.g)- Exercice 21 page 483 : Chaufferette chimique.h)- Exercice 24 page 485 : Titrage de l’acide lactique dans le lait. |
|
Définition du dosage par
étalonnage: la concentration d’une espèce en solution en comparant une grandeur physique, caractéristique de la
solution, à la même grandeur physique mesurée pour des solutions
étalon. |
2)- Les
différents types de dosage.
-
Dosage avec un spectrophotomètre.
-
Dosage avec un conductimètre
(titrage conductimétrique).
-
Dosage avec un pH-mètre (titrage
pH-métrique).
-
Dosage avec un indicateur coloré
(titrage colorimétrique).
II- Dosage avec un spectrophotomètre.
1)- Le
spectrophotomètre. (Chap. N° 04 Analyse spectrale. Cours)
a)-
Mesure de l’absorbance d’une
solution par spectrophotométrie.
-
On utilise le fait que toute
solution colorée absorbe la lumière visible (400 nm <
λ0
< 800 nm).
-
Lorsqu’un faisceau de lumière
monochromatique traverse un milieu absorbant, l’intensité
lumineuse I
du faisceau transmis est inférieure à
l’intensité lumineuse I0 du faisceau incident.
-
Pour évaluer cette diminution, on
utilise :
-
La transmittance
T : 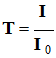
-
L’absorbance A :
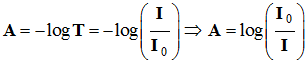
-
La transmittance s’exprime en
pourcentage.
-
À une transmittance
T de
100 % (T = 1) correspond une absorbance nulle :
A
= 0.
-
à une
transmittance de 1 % (T = 0,01) correspond une absorbance
A = log 100 = 2.
-
Exemple de réaction :
-
On peut utiliser cette méthode
lorsqu’une espèce colorée se forme ou disparaît au cours de la
réaction.
-
Réaction entre l’eau oxygénée et
les ions iodure en milieu acide : il se forme du diiode qui est
une espèce chimique colorée.
-
Équation de la réaction :
|
H2O2 (aq)
+ 2
H+(aq)
+ 2
I-
(aq)
®
2
H2O |
|
Réaction lente |
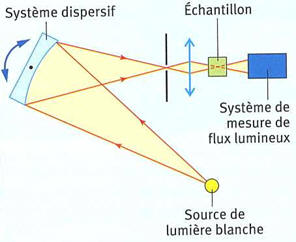
b)-
Principe de fonctionnement.
|
|
|
|
-
Un système dispersif (prisme ou
réseau) permet de sélectionner une radiation lumineuse de
longueur d’onde λ donnée.
- Cette radiation est dirigée vers l’échantillon à analyser.
- Le flux lumineux transmis est mesuré
et converti en valeur d’absorbance A.
c)-
Absorbance en fonction de la
longueur d’onde.
-
L’absorbance A d’une solution
colorée dépend de la longueur d’onde λ de la radiation lumineuse
utilisée.
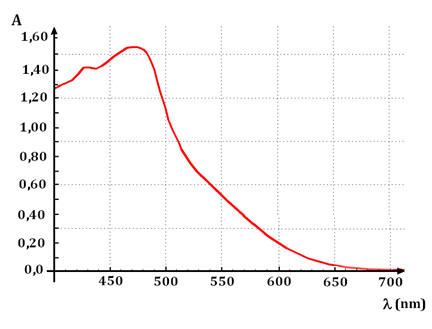
-
On donne l’absorbance d’une
solution de diiode en fonction de la longueur d’onde :
-
Pour une solution de diiode de
concentration C
= 1,0
mmol / L,
on mesure l’absorbance A pour différentes longueurs
d’ondes.
-
La plage de variation de la
longueur d’onde se situe dans l’intervalle suivant :
-
400
nm < λ < 700 nm.
-
On règle la longueur d’onde λ sur
la valeur souhaitée, on fait le blanc avec la solution étalon,
puis on mesure l’absorbance.
-
Il faut répéter le mode
opératoire pour chaque mesure.
-
Courbe obtenue :
2)-
Absorbance en fonction de la concentration.
(Chim N° 02 Changement de couleur et réaction chimique. Cours)
a)-
Réglage du spectrophotomètre.
-
Pour réaliser les mesures
d’absorbance, le spectrophotomètre est généralement réglé sur la
longueur d’onde
λmax
correspondant au maximum d’absorption du spectre de la solution
étudiée.
-
À cette longueur d’onde, la
valeur de l’absorbance étant la plus grande, l’incertitude sur
la mesure est la plus petite.
-
Pour les solutions aqueuses de
diiode, on choisit λ = 450 nm, pour avoir le maximum de
variations pour la valeur de A.
-
On n’a pas choisi
λ = 475 nm car
le spectrophotomètre sature en fin d’expérience lorsque la
concentration en diiode devient trop grande.
b)-
Préparation des solutions et
mesures :
-
On dispose d’une solution
S0
de concentration en diiode C0 = 1,0 mmol / L.
-
À partir de S0,
préparer les solutions 10 mL de solution
S en utilisant
les solutions présentes dans les burettes.
-
Matériel :
-
Préparer la solution
S et
réaliser la mesure de l’absorbance de la solution préparée.
|
Groupes |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Solution S mmol / L |
0,10 |
0,20 |
0,30 |
0,40 |
0,50 |
0,60 |
0,70 |
0,80 |
0,90 |
1,0 |
|
Absorbance A g1 |
0.120 |
0.256 |
0.435 |
0.578 |
0.723 |
0.818 |
0.997 |
1.149 |
1.281 |
1.404 |
|
Absorbance A g2 |
0.096
|
0.228
|
0.361
|
0.508
|
0.628
|
0.723
|
0.878
|
1.053
|
1.109
|
1.261
|
- Pour préparer la solution S, on mélange la solution de diiode de concentration C0 = 1,0 mmol / L et
-
La solution d’iodure de potassium de
concentration C = 0,20 mol / L.
- Pour préparer la solution 1, on mélange à l’aide des burettes graduées, 1 mL de solution de diiode de concentration :
- C0 = 1,0 mmol / L et 9
mL de solution d’iodure de potassium de concentration
C = 0,20 mol / L.
- Pour préparer la solution 2, on mélange à l’aide des burettes graduées, 2 mL de solution de diiode de concentration :
- C0 = 1,0 mmol / L et 8
mL de solution d’iodure de potassium de concentration
C = 0,20 mol / L.
-
Ainsi de suite….
-
On trace la courbe
A
= f (C).
-
Courbe obtenu par le Groupe 1 :
-
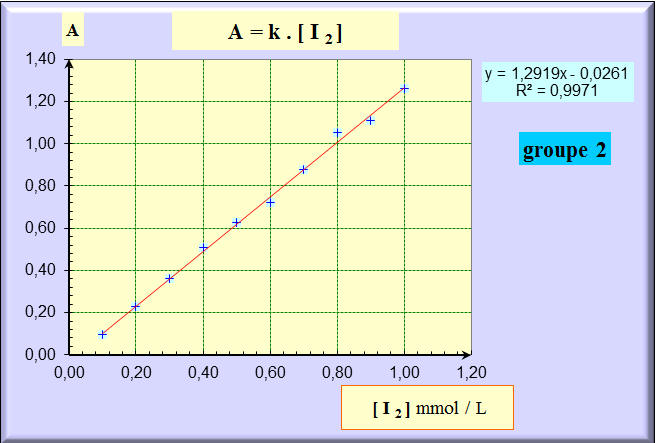
Courbe obtenue par le Groupe 2 :
-
On obtient la courbe
d’étalonnage.
-
Ce graphe est une portion de
droite passant par l’origine.
-
L’absorbance A est
proportionnelle à la concentration C de la solution de
diiode dans le domaine étudié.
-
A =
k . [I2].
-
On peut généraliser ce résultat à
toutes les solutions colorées.
-
Pour les solutions suffisamment
diluées, l’absorbance est proportionnelle à la concentration de
l’espèce colorée.
|
► Définition : - L’absorbance d’une solution diluée contenant une espèce colorée est proportionnelle à la concentration (effective) C de cette espèce et à
l’épaisseur ℓ (cm) de la solution traversée par le faisceau
lumineux. - A (λ) =
ε (λ).ℓ.C |
|
ε (λ) : - ε (λ) est appelé
coefficient d’extinction molaire ou coefficient d’absorption
molaire. - Il dépend de la nature de
l’espèce dissoute et de la longueur d’onde de la radiation
utilisée. - Il dépend également du solvant et
de la température. |
-
Unités :
- L'absorbance A : sans unité ;
- L'épaisseur de la cuve : ℓ en cm
- Le coefficient
d'absorption molaire : ε (λ) en mol
– 1.L.cm
– 1.
- La courbe A = f (C)
-
Elle
constitue la courbe d’étalonnage de la substance étudiée.
-
Elle permet de déterminer la
concentration d’une solution de la substance étudiée.
-
Elle permet donc de doser une
espèce chimique colorée.
-
Afin d’augmenter la sensibilité
de la méthode, on utilise la longueur d’onde qui correspond au
maximum d’absorption de la substance étudiée.
-
Cette méthode est alors beaucoup
plus précise que la méthode colorimétrique utilisant une échelle
des teintes.
- Remarque :
-
La solution colorée
doit être suffisamment diluée, C
≤ 1,0
x 10–2 mol . L–1, et le
spectrophotomètre ne doit pas saturer.
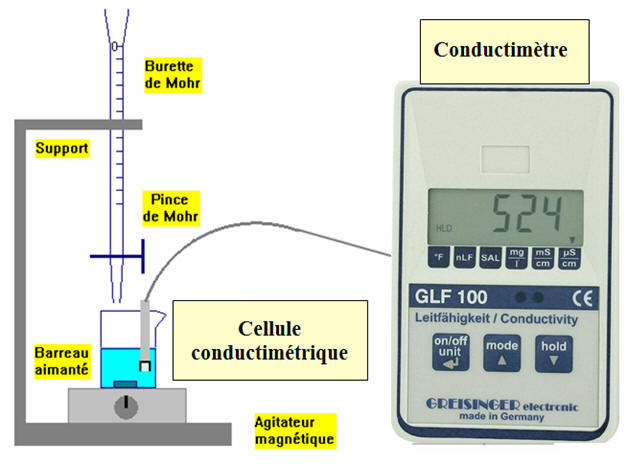
III- Dosage avec un conductimètre.
1)- Le
conductimètre.
Titrage
conductimétrique
|
Le conductimètre est constitué : - D'une sonde de conductimétrie (deux plaques conductrices en
vis-à-vis,alimentées par une tension alternative. - D'un boîtier qui sert
d'alimentation pour la sonde. - Ce boîtier dispose en outre d'une zone de lecture, d'un bouton de réglage
de la température et d'un bouton d'étalonnage.
- Un troisième bouton
permet en général de sélectionner le calibre. |
-
Régler le bouton de température
du conductimètre sur la température de la pièce.
-
Rincer (avec de l'eau distillée)
et essuyer délicatement (avec du papier Joseph) la sonde.
-
Plonger la sonde dans une
solution d'étalonnage.
-
Régler le bouton d'étalonnage du
conductimètre pour que la valeur affichée coïncide avec la
valeur donnée par le fabriquant de la solution d'étalonnage (à
la température de la pièce).
-
Sortir la sonde de la solution
d'étalonnage, la rincer, la replacer dans l'eau distillée.
- Rincer la sonde de conductimétrie (si possible avec la solution dont on veut mesurer la conductivité).
- L'essuyer délicatement avec du papier Joseph.
-
Plonger la sonde dans la solution
dont on veut mesurer la conductivité.
-
Attendre la stabilité (quelques
secondes).
-
Lorsque la lecture est terminée,
rincer la sonde et la plonger dans la solution d'eau.
|
Détermination de la concentration
d’une solution L’hypocalcémie, carence de l’organisme en élément calcium, peut être traitée par injection intraveineuse d’une solution de
chlorure de calcium (Ca2+
(aq) + 2
Cl–
(aq)). Pour déterminer sa concentration
C, on
utilise une méthode conductimétrique. 1. On dispose, pour étalonner la cellule conductimétrique, de solutions étalons Si
de concentrations connues
Ci.
- Le tableau suivant
fournit les conductances Gi
de ces différentes
solutions.
- Tracer la courbe G
= f (C). 2. Le contenu d’une ampoule de solution injectable a été dilué 100 fois. La mesure de la conductance de la solution diluée, avec la même cellule
conductimétrique et à la même
température, donne :
G’ = 2,71 mS.
a. Déterminer la valeur
de la concentration C’ de la solution diluée.
b. En déduire la
concentration C de la solution injectable.
c. Pourquoi a-t-il été
nécessaire de diluer cette solution ? 3. Déterminer l’apport calcique, c’est-à-dire la quantité d’élément calcium,
d’une ampoule de solution injectable de
10,0 mL. |
Correction :
|
Détermination de la concentration d’une solution
1. Courbe G =
f (C). - Les points sont sensiblement alignés.
- On peut tracer la droite
moyenne.
- Avec le tableur
Excel, on ajoute une courbe de tendance et comme
modèle ‘’linéaire’’
- La courbe obtenue est
une droite qui passe pratiquement par l’origine.
- On peut affirmer que la conductance de la solution est proportionnelle
à
la concentration de la solution, ceci dans le
domaine étudié.
-
On tire : G
(mS) = 0,588 C (mmol / L)
2. Conductance de la
solution diluée
a. Concentration C’
de la solution diluée.
-
Exploitation
graphique : C’
» 4,6
mmol / L
» 4,6
× 10– 3 mol / L
b. Concentration C
de la solution injectable.
- C
= 100 C’
- C
≈ 100
× 4,6
× 10– 3
-
C
≈ 4,6
×
10– 1
mol / L
c. Pourquoi a-t-il été
nécessaire de diluer cette solution ?
- La concentration de
la solution injectable est supérieure
à la
concentration de la solution S0.
- Elle n’appartient pas
au domaine d’étude.
- La loi n’est plus
vérifiée pour les solutions trop concentrées.
3. Apport calcique d’une
ampoule de solution injectable de 10,0 mL.
- Par définition : n
(Ca2+) = [Ca2+] .
V
- n
(Ca2+)
≈
4,6
×
10– 1
× 10,0
× 10– 3
-
n
(Ca2+)
≈
4,6
× 10– 3 mol |
a)-
La conductivité d’une solution
ionique (rappels).
-
Cellule
conductimétrique :
![]() Mesure de la conductance d’une
solution de chlorure de sodium :
Mesure de la conductance d’une
solution de chlorure de sodium :
► Dispositif expérimental. :
Conductance et facteur d’influence.
-
Réglages : On choisit le signal
sinusoïdal et
-
On règle la fréquence du G.B.F
sur 500 Hz.
-
Et on règle la tension
U
aux bornes de la cellule sur 1,00 V.
-
On choisit la cellule
conductimétrique :
S = 1 cm2 et
ℓ = 1 cm
-
Solution de chlorure de sodium de
concentration C = 5,0
× 10– 3
mol / L.
|
I = 1,08
mA |
Valeur de la conductance :
|
|
U = 1,00
V |
|
|
f = 500
Hz |
-
Avant chaque mesure, il faut
rincer les électrodes à l’eau distillée.
-
Essuyer délicatement les
électrodes avec du papier absorbant, agiter doucement la cellule
dans la solution pour bien homogénéiser.
-
La conductance G est
proportionnelle à la concentration C de la solution si
C < 1,0
× 10–2 mol / L.
-
G = k’
. C
-
D’autre part :
-
La conductance G
d’une portion de solution est proportionnelle au rapport
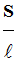 .
.
-
Par définition, le
coefficient de proportionnalité est appelé : conductivité de la
solution ionique que l’on note
σ ‘’sigma
minuscule’’.
-
On écrit :
|
|
G est la
conductance en siemens S |
|
S :
surface
des électrodes en m2. |
|
|
ℓ :
distance entre les électrodes en m. |
|
|
σ : conductivité de la solution en S . m– 1 |
-
La grandeur σ est caractéristique de la solution.
-
Elle rend compte de la capacité de la solution à conduire le
courant électrique.
-
Elle ne dépend pas de la géométrie de la cellule.
-
La grandeur σ est liée à la nature et la concentration
des ions présents dans la solution.
b)-
Conductivité molaire ionique
(rappels).
-
À chaque ion d’une solution
ionique, on affecte une conductivité molaire ionique
λ.
-
La conductivité molaire ionique
se rapporte à un ion donné.
-
Elle dépend de la température, de
la nature du solvant.
-
Elle ne dépend pas de la
concentration si C
< 1,0
× 10–2 mol / L.
-
Exemple pour les ions sodium, on
écrit :
λ (Na
+) = 5,01 × 10– 3 S.m2.mol–
1 dans l’eau.
-
Pour les ions chlorure :
λ (Cl
–) = 7,63
× 10– 3 S.m2.mol– 1 dans
l’eau.
-
Remarque :
-
Dans une solution électrolytique,
ce sont les ions qui sont responsables du passage du courant.
-
Un courant dans une solution est
dû à la circulation des ions positifs et négatifs se déplaçant
en sens inverse.
-
Chaque ion dans la solution
contribue à la conductivité de celle-ci.
-
La conductivité
σ de la solution est égale à la somme des
conductivités due aux cations et aux anions.
-
On écrit :
-
σ
=
σ (+) +
σ (–)
-
Formule générale :
-
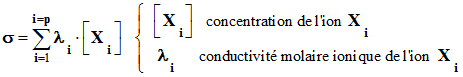
-
La conductivité
σ d’une solution ionique dépend de la nature des ions
présents Xi et de leur concentration
[ Xi
] respectives.
-
Exemple :
-
Pour une solution de chlorure de
sodium :
-
Solution de chlorure de sodium :
|
|
eau |
|
|
|
|
NaCl (s) |
→ |
Na+
(aq) |
+ |
Cl–
(aq) |
-
Or :
C
= [
Cl
–
] = [
Na
+
]
-
σ
=
λ
(Cl
–)
. [
Cl
–
] +
λ
(Na
+)
. [
Na
+
]
-
σ
= {λ
(Cl
–)
+
λ
(Na
+)
}
.C
-
Solution de chlorure de baryum :
|
|
eau |
|
|
|
|
BaCl2
(s) |
→ |
Ba2+
(aq) |
+ |
2 Cl–
(aq) |
-
Or :
[
Ba2+
] = C
et [
Cl–
] = 2 C
-
σ
=
λ
(Cl–)
. [
Cl–
] +
λ
(Ba2+)
. [
Ba2+
]
-
Expression en fonction de
C
:
-
σ
=
λ
(Cl–).2
C
+
λ
(Ba2+).
C
-
σ
=
(2
λ
(Cl–).+
λ
(Ba2+)
).C
► Remarque :
-
σ
= k . C
c)-
Énoncé de la loi de Kohlrausch
-
La conductivité
σ d’une solution diluée d’une espèce ionique dissoute
est proportionnelle à sa concentration molaire en soluté
apporté :
-
σ =
k .
C.
|
σ =
k .
C |
C ;
concentration en mol . L– 1 |
|
k :
coefficient de proportionnalité en S . L .
m– 1. mol– 1 |
|
|
σ :
conductivité de la solution en S . m– 1 |
-
À partir de la mesure de la
conductivité d’une solution, on peut déterminer la valeur de sa
concentration.
-
Remarque :
-
On peut le faire aussi à partir
de la valeur de la conductance si on ne possède pas de
conductimètre.
-
Remarque :
-
Les lois de Beer-Lambert et
Kohlrausch ont des équations analogues.
-
La solution colorée doit être
suffisamment diluée, C
≤ 1,0
× 10–2 mol . L–1, et ne doit
contenir qu’un seul soluté ionique.
IV- Dosage par titrage direct.
1)-
Réaction de support de dosage.
-
Un dosage par titrage direct met
en jeu une réaction chimique.
-
La réaction de support de dosage
est une réaction : totale, rapide, unique.
-
C’est une réaction quantitative.
-
Un réactif titrant, de
concentration connue, réagit avec un réactif titré dont on
cherche la concentration.
-
Le réactif titré peut être placé,
selon le cas, dans un bécher ou dans une burette graduée.
-
Le suivi du titrage peut être
réalisé de différentes façons :
-
Par conductimétrie,
-
Par pH-métrie,
-
Par colorimétrie.
-
Cette méthode de dosage est
destructive, car la réaction chimique consomme l’espèce à doser.
-
Mais on travaille toujours avec
de petites quantités.
-
Schéma du montage :
-
Dosage pH-métrique :
-
Suivi pH-métrique d'une réaction acido-basique :
Suivi
ph-métrique d’une réaction acido-basique.
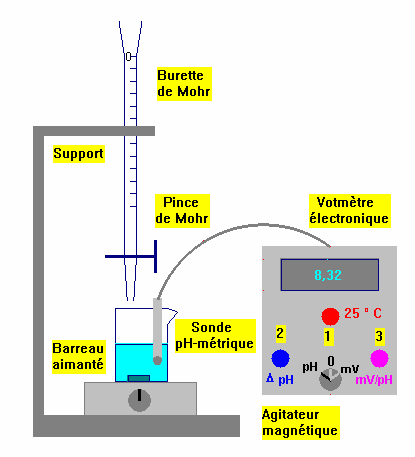
- Dosage colorimétrique : Détermination de la concentration des ions fer II d’une solution de sel de Mohr :
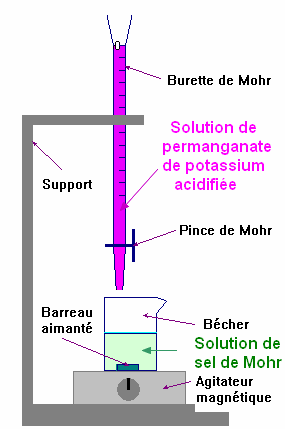
-
Dosage d’un déboucheur ou
d’un détartrant :
Dosage
d’un déboucheur et d’un détartrant.
-
L’équivalence d’un titrage est
atteinte lorsque le réactif titrant et le réactif titré sont
dans les proportions stœchiométriques.
- Les deux réactifs sont alors totalement consommés.
- Ils ont totalement disparu.
-
Le repérage de l’équivalence
dépend de la technique de dosage utilisée.
4)-
Relations à l’équivalence d’un titrage.
-
Dans un bécher, on verse un
volume VA de concentration inconnue
CA
du réactif A.
-
Une burette graduée est remplie
du réactif B de concentration connue
CB.
-
On verse progressivement la
solution de réactif B dans le bécher.
-
À l’équivalence, on a versé le
volume équivalent
VE de solution
B.
-
Pour connaître les relations
d’équivalence, il faut dresser le tableau d’avancement de la
réaction.
-
Tout en sachant qu’à
l’équivalence ;
-
Les réactifs sont totalement
consommés.
-
On a versé la quantité de matière
nE =
CB .
VE
de réactif B.
|
Équation de
titrage |
a A
|
+
b B |
→ |
c C |
+
d D |
|
|
État du
système |
Avancement |
n (A) |
n (B) |
|
n (C) |
n (D) |
|
État initial
à
l’équivalence |
x = 0 |
n0
(A) =
CA
. VA |
nE
(B) =
CB
. VE |
0 |
0 |
|
|
État final
à
l’équivalence |
xE
= xmax |
n0
(A) –
a . xE
= 0 |
nE
(B) –
b .
xE
= 0 |
|
c
.
xE |
d . xE |
|
|
CA
. VA
–
a . xE
= 0 |
CB
. VE
–
b .
xE
= 0 |
|
|
|
|
-
Relations à l’équivalence :
-
n0 (A) –
a .
xE
= 0 et
nE (B) –
b .
xE = 0
-
On tire :
-
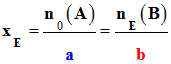
-
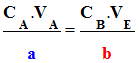
-
On peut utiliser le tableau
réduit suivant :
|
Équation de titrage |
a A |
+
b B |
→ |
c C |
+
d D |
|
Quantités de
matières à l’équivalence |
n0
(A) |
nE
(B)
|
|
|
|
|
Coefficients
stœchiométriques |
a |
b |
|
|
|
|
Relation 1 |
|
|
|
|
|
|
Équation de titrage |
a A |
+
b B |
→ |
c C |
+
d D |
|
Quantités de
matières à l’équivalence |
CA
. VA |
CB
. VE |
|
|
|
|
Coefficients
stœchiométriques |
a |
b |
|
|
|
|
Relation 2 |
|
|
|
|
|
V- Repérage de l’équivalence d’un titrage direct.
1)- Cas
d’un titrage conductimétrique.
-
Un titrage conductimétrique peut
être envisagé lorsque la réaction support de titrage fait
intervenir des ions.
-
Si au cours d’un titrage
conductimétrique la dilution est négligeable, le graphe
σ =
f (Vréactif ajouté) est
constitué de deux droites.
-
Le point d’intersection de ces
droites permet de repérer l’équivalence du titrage.
-
Remarque :
-
Si on ne possède pas de
conductimètre, on peut utiliser une cellule conductimétrique et
le montage suivant et travailler avec la conductance de la
solution :
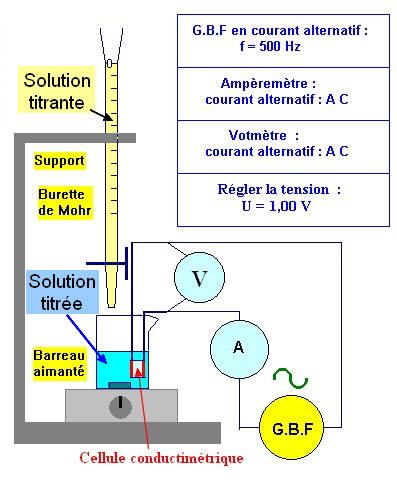
b)-
Titrage conductimétrique d’un
produit ménager.
c)-
Exercice 10 page 479. Évolution
de la conductivité lors d’un titrage.
|
On dose, par titrage conductimétrique, une solution SA d’acide chlorhydrique {H3O+ (aq) + Cl– (aq)}, par une solution
SB
d’hydroxyde de sodium, {Na+
(aq) + HO–
(aq)}. L’équation de la réaction de
titrage est :
H3O+
(aq) + HO–
(aq) → 2 H2O
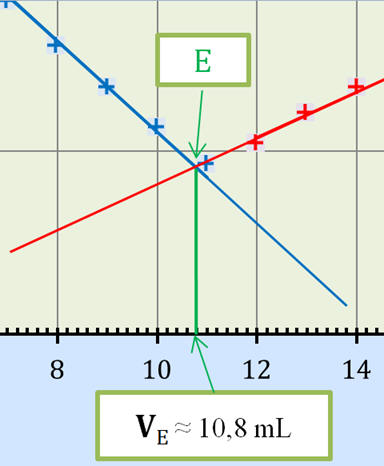
(ℓ) Le suivi du titrage par
conductimétrie permet de tracer le graphe
σ =
f (VB)
ci-dessous.
1. Faire un schéma légendé du
dispositif de titrage.
2. Déterminer le volume
équivalent VE
du titrage. On néglige la dilution lors du
titrage.
3.
On se place avant
l’équivalence.
a. Quel est le réactif
limitant.
b. La concentration en ions
chlorure varie-telle au cours du titrage ?
c. L’expression de la
conductivité
σ de la solution contenue dans le bécher est :
σ =
λ (H3O+)
. [H3O+]
+ λ (Na+)
. [Na+]
+ λ (Cl–)
. [Cl–] - Sachant que λ
(H3O+) > λ
(Na+), justifier l’évolution de la
conductivité σ avant l’équivalence.
4. On se place maintenant après
l’équivalence.
a. Quel est le réactif
limitant ?
b.
Établir l’expression de la
conductivité
σ.
c. Justifier l’évolution de la
conductivité
σ de la solution contenue dans le bécher après
l’équivalence du titrage. |
|
1. Schéma légendé du dispositif
de titrage.
2. Valeur du volume équivalent
VE
du titrage. - Exploitation du
graphe
σ = f (VB) :
- VE
≈ 10,8 mL
3. On se place avant
l’équivalence.
a. Réactif limitant. - L’équation de la
réaction de titrage est : H3O+
(aq) + HO– (aq) → 2 H2O
(ℓ) - Notations : - Solution SA
d’acide chlorhydrique : concentration CA
et volume VA - Solution SB
d’hydroxyde de sodium : concentration CB
et volume VB (VB
varie de 0 mL à 22 mL) - On peut dresser le
tableau d’avancement suivant : - On verse la solution
d’hydroxyde de sodium dans la solution d’acide
chlorhydrique.
- Avant l’équivalence,
VB
< VE et CB .
VB
<
xE. -
Le réactif limitant
est l’ion hydroxyde, il est totalement consommé.
b. Variation de la
concentration des ions chlorure au cours du titrage -
- La concentration des ions chlorure diminue par effet de dilution. - Mais comme, on néglige la dilution au cours du titrage, [Cl–] est pratiquement constante. - Les ions chlorure ne
participent pas à la réaction de titrage : ions
spectateurs. - Pour que l’effet de
dilution soit négligeable,
on ajoute
environ V = 250
mL d’eau distillée. - Ainsi : - V >>
VB - Au départ : -
- Après l’ajout du
volume VB de solution d’hydroxyde
de sodium, avec V >>
VB -
c. Évolution de la conductivité
σ avant
l’équivalence :
► Avant l’équivalence,
les ions présents sont :
- Les ions oxonium
H3O+, les ions chlorure Cl–,
et les ions sodium
Na+.
- Les ions hydroxyde HO–
ne sont pas
présents car ils sont totalement consommés. - Au cours de la
réaction, les ions oxonium disparaissent
H3O+ et ils sont remplacés par
des
ions sodium
Na+.
- La concentration en ions oxonium H3O+ diminue, la concentration en ion sodium augmente Na+et la concentration en ions chlorure Cl–
ne varie pratiquement pas. - Comme λ (H3O+)
> λ (Na+), la conductivité
globale σ de la solution diminue avant
l’équivalence
4. On se place maintenant après
l’équivalence.
a. Réactif limitant - Après l’équivalence,
VB
> VE et CB .
VB
>
xE. - Le réactif limitant
est l’ion oxonium, il est totalement consommé.
b. Expression de la
conductivité
σ. - σ = λ (HO–)
. [HO–] + λ (Na+)
. [Na+] + λ (Cl–)
. [Cl–]
c. Évolution de la conductivité
σ de la
solution contenue dans le bécher après l’équivalence
du titrage. - La conductivité globale σ de la solution augmente après l’équivalence car on ajoute des ions hydroxyde HO–
et des ions sodium Na+ dans le
mélange réactionnel.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d)-
Dosage des ions chlorure dans le
lait. Exercice 19 page 482.
|
Une inflammation des mamelles des vaches rend le lait impropre à la consommation. Or cette inflammation se traduit par une
augmentation de la concentration
en ions sodium
Na+
(aq) et chlorure
Cl–
(aq). Une mesure de la conductivité du lait, après la traite, permet de déterminer sa concentration en ions chlorure Cl– (aq)
et
donc de vérifier s’il est consommable.
Pour
réaliser ce titrage, un lait frais est dilué 5 fois.
Soit S1
la solution de lait diluée et
C1
sa concentration en ions chlorure.
On verse
un volume V1
= 10,0 mL de solution
S1
dans un bécher et on ajoute
environ 250 mL d’eau
distillée.
On
mélange, puis on plonge dans le bécher une cellule
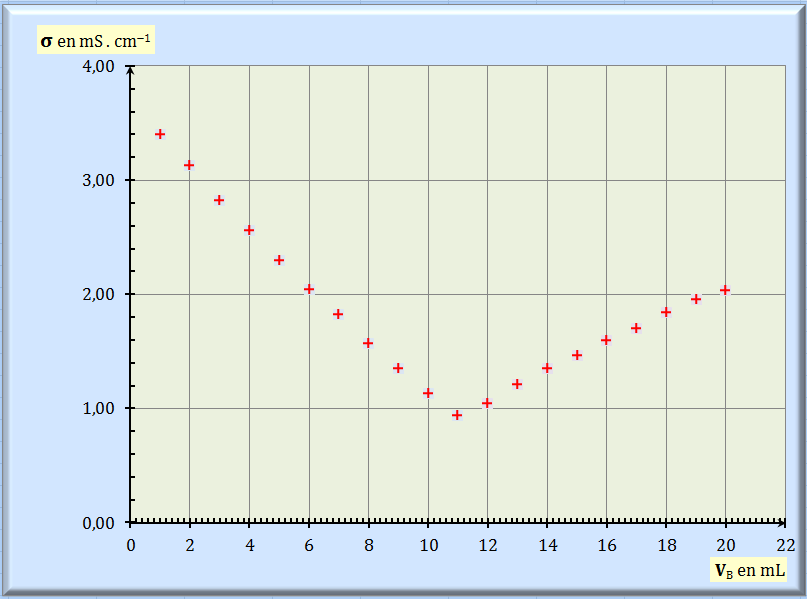
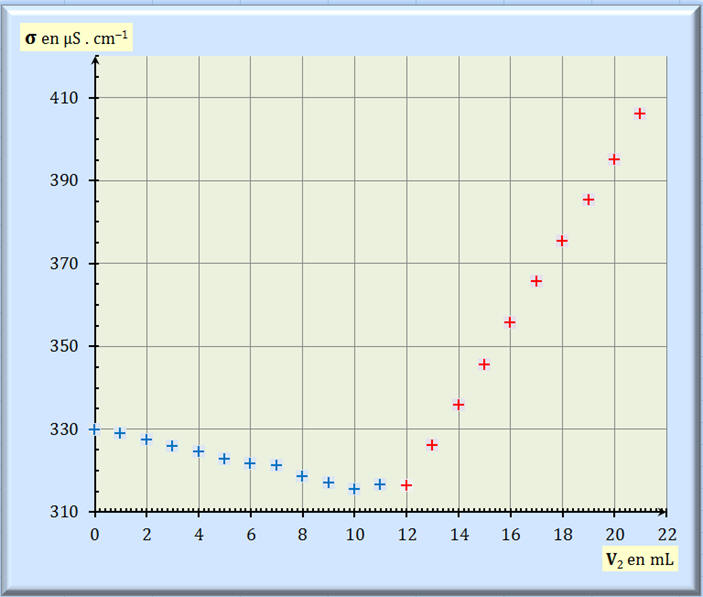
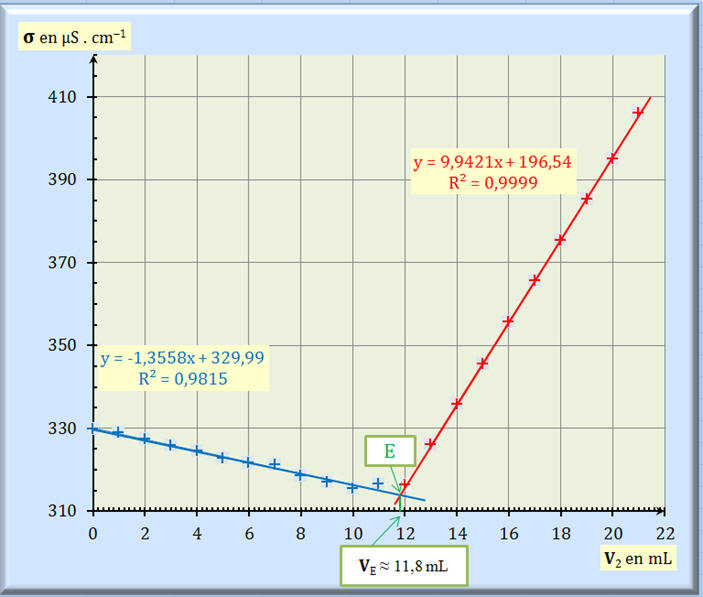
conductimétrique. Initialement et après chaque ajout millilitre par millilitre d’une solution S2 de nitrate d’argent {Ag+ (aq) + NO3– (aq)}, de concentration C2 = 5,00 × 10–3 mol . L–1,
on mesure la
valeur de
la conductivité
σ
de la solution et on obtient la courbe suivante : La réaction, rapide, met
uniquement en jeu les ions chlorure et les ions
argent selon l’équation :
Ag+
(aq) + Cl–
(aq) →
AgCl (s)
1. Pourquoi la conductivité
initiale de la solution
S1
n’est-elle pas nulle ?
2. Pourquoi ajoute-t-on un
volume d’environ 250 mL d’eau distillée dans le
bécher ?
3. Déterminer graphiquement le
volume VE
de solution de nitrate d’argent versé à
l’équivalence.
4. La conductivité de la
solution peut s’écrire : -
a. Montrer que la conductivité
dans le bécher, en un point du titrage avant
l’équivalence, s’écrit : - - Où σ0 est la conductivité de tous les ions spectateurs initialement présents dans le lait et Vtot est le volume de la
solution dans le bécher.
b. Justifier la diminution de
la conductivité
σ du
milieu réactionnel avant l’équivalence.
5.
Établir l’expression de la
conductivité dans le bécher après l’équivalence, et
justifier son évolution. 6. Déterminer la concentration molaire C1 en ions chlorure initialement présents dans la solution S1,
puis la concentration
C0
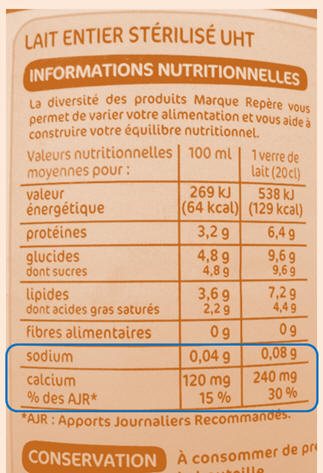
en ions chlorure du lait. 7. Dans le lait frais analysé, la concentration massique moyenne en ions chlorure se situe entre 0,8 g . L–1 et 1,2 g . L–1.
Le lait analysé est-il consommable ? - Données : - λ1 =
λ (Cl–)
= 76,3
× 10–4 m2 . S . mol–1 - λ2 =
λ (NO3–)
= 71,4
× 10–4 m2 . S . mol–1 - λ3 =
λ (Ag+)
= 61,9
× 10–4 m2 . S . mol–1
|
|
1. La
conductivité initiale de la solution
S1
n’est
pas nulle : - Initialement, la solution est une solution diluée de lait frais. - Le lait frais contient des sels minéraux en solution aqueuse. - Le lait contient des ions sodium Na+ (aq), des ions chlorure Cl– (aq), des ions calcium Ca2+ (aq),
des ions magnésiums Mg2+ (aq), … - Étiquette d’une
bouteille de lait ½ écrémé :
- La conductivité
initiale
σ0 de la solution S1
n’est pas nulle car c’est une solution
électrolytique.
2. On ajoute un volume
d’environ 250 mL d’eau distillée dans le bécher : - Le fait d’ajouter un volume d’eau distillée de 250 mL permet de travailler avec un grand volume de solution. - Ainsi le phénomène de dilution peut être négligé lors de l’ajout - de la solution
S2
de nitrate d’argent {Ag+ (aq) +
NO3– (aq)}
(solution titrante).
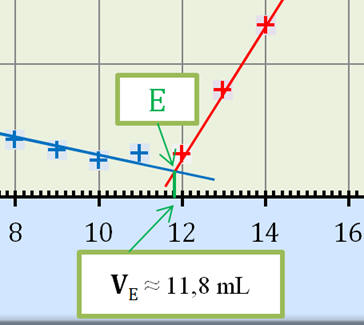
3. Détermination graphique
du volume
VE
de solution de nitrate d’argent versé à
l’équivalence. - Exploitation du
graphe
σ = f (V2) :
- VE
≈ 11,8 mL
4. Conductivité de la solution:
a. Expression de la conductivité dans le bécher, en un point du titrage avant l’équivalence :-
Les ions présents
avant l’équivalence : - On se place dans le
cas où le volume de solution S2 :
V2 < VE : - σ0 est la conductivité de tous
les ions spectateurs initialement présents dans le
lait : - On verse la solution S2 de nitrate d’argent {Ag+ (aq) + NO3– (aq)},
les
ions argent Ag+ (aq) sont
totalement consommés. - Les ions
nitrate NO3–(aq),
qui ont été rajoutés, ne participent pas à la
réaction : -
- Des ions chlorure ont
été consommés : -
- L’effet de
dilution est négligeable : -
On peut donner la
relation simplifiée pour la conductivité de la
solution avant l’équivalence : - σ =
σ0 +
λ
(NO3–)
. [NO3–]
+
λ (Cl–)
. [Cl–] -
-
b. Justification la diminution
de la conductivité
σ du
milieu réactionnel avant l’équivalence. - - On remarque que
λ1 >
λ2 et que V2
augmente au fur et à mesure que l’on verse la
solution S2 de nitrate d’argent. - Conclusion : - La
conductivité σ du milieu réactionnel diminue
avant l’équivalence car : -
λ2
–
λ1 < 0 et V2
↑.
5. Expression de la
conductivité dans le bécher après l’équivalence, et
justification de son évolution. - Après l’équivalence,
V2 > VE. - Les ions chlorure
sont totalement consommés, il reste des ions argent
et des ions nitrate : - -
- σ =
σ0 +
λ (NO3–)
. [NO3–]
+
λ (Ag+)
. [Ag+] -
- La valeur du volume V2 augmente au fur et à mesure que l’on verse la solution S2 de nitrate d’argent,
il découle de ceci que la valeur
de la conductivité σ du milieu réactionnel
augmente après l’équivalence.
► Récapitulatif :
Tableau d’avancement
- On verse la solution
de nitrate d’argent dans la solution de lait (qui
contient les ions chlorure).
6. Concentration molaire C1 en ions chlorure initialement présents dans la solution S1,
puis la concentration
C0
en ions chlorure du lait. - Relation à
l’équivalence : xE
= C1 . V1 =
C2 . VE - Concentration molaire
C1 en ions chlorure initialement
présents dans la solution S1 - - Concentration C0
en ions chlorure du lait : - C0 = 5
C1 - C0
≈ 5
× 5,9
× 10–3 - C0
≈ 3,0
× 10–2 mol . L–1
7. Le lait
analysé est-il consommable ? - Concentration
massique du lait analysé : - t0
(Cl–) = C0 .
M (Cl–)
≈ 3,0
× 10–2
× 35,5 - t0
(Cl–)
≈ 1,0 g . L–1 - Le lait analysé est
consommable, la valeur mesurée se trouve dans
l’intervalle autorisé. - 0,8 g . L–1 ≤ t0
(Cl–)
≤
1,2 g . L–1
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2)- Cas
d’un titrage par pH-métrie.
-
Un titrage pH-métrique peut être
envisagé lorsque la réaction support du titrage est une réaction
acido-basique.
► Réaction chimique entre l’acide
chlorhydrique et la soude :
-
Acide chlorhydrique :
H3O+
(aq)
+
Cl –
(aq)
-
Soude : Na+
(aq) + HO– (aq)
-
L’équation de la réaction de
titrage est :
H3O+
(aq) + HO–
(aq) → 2 H2O
(ℓ)
|
► Dispositif expérimental : - On prélève un volume VA = 10,0 mL de la solution d’acide chlorhydrique à l'aide de la pipette jaugée (10,0 mL) et on les verse dans un autre bécher ou
un erlenmeyer. - On ajoute environ 10 mL
d'eau distillée pour que la sonde du pH-mètre soit
totalement immergée. - On peut ajouter quelques gouttes
d’un indicateur coloré (B.B.T, phénolphtaléine ou hélianthine). - On place le barreau aimanté et on
maintient une agitation douce. - On remplit la burette graduée de soude de concentration : - CB = 1,0
× 10–1 mol.L–1 - On règle au zéro de la
graduation. |
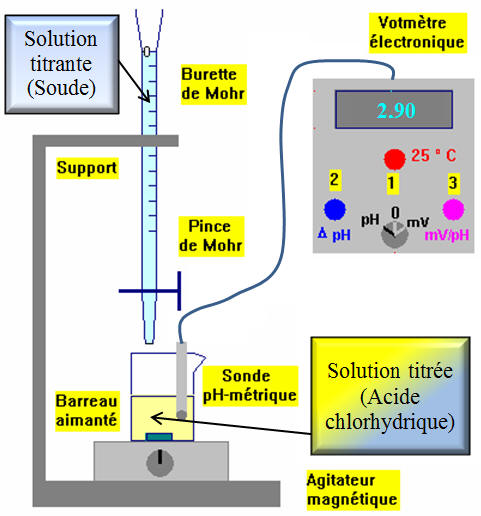
► Mesures :
- On verse progressivement la solution de soude dans la solution d'acide et on relève la valeur du pH après chaque ajout.
- On adapte les volumes
VB
versés aux variations de
pH
-
Tableau des valeurs :
|
VB
mL |
0,0 |
1,0 |
2,0 |
3,0 |
4,0 |
5,0 |
6,0 |
7,0 |
8,0 |
8,5 |
8,8 |
9,0 |
9,2 |
|
pH |
1,70 |
1,75 |
1,77 |
1,82 |
1,90 |
1,98 |
2,08 |
2,21 |
2,40 |
2,55 |
2,67 |
2,81 |
2,96 |
|
VB
mL |
9,5 |
9,7 |
10 |
10,2 |
10,5 |
10,7 |
11 |
11,5 |
12 |
13 |
17 |
18 |
20 |
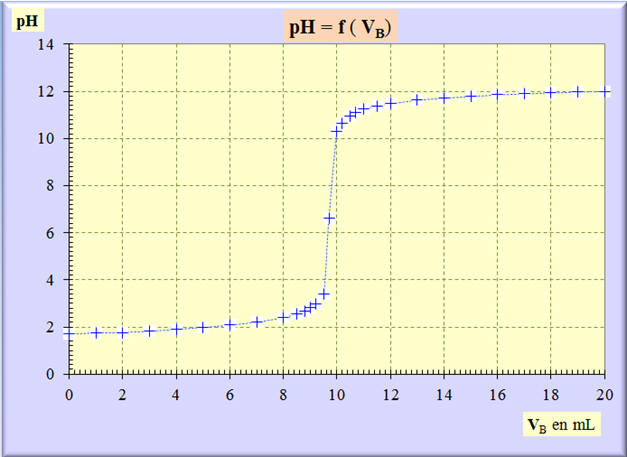
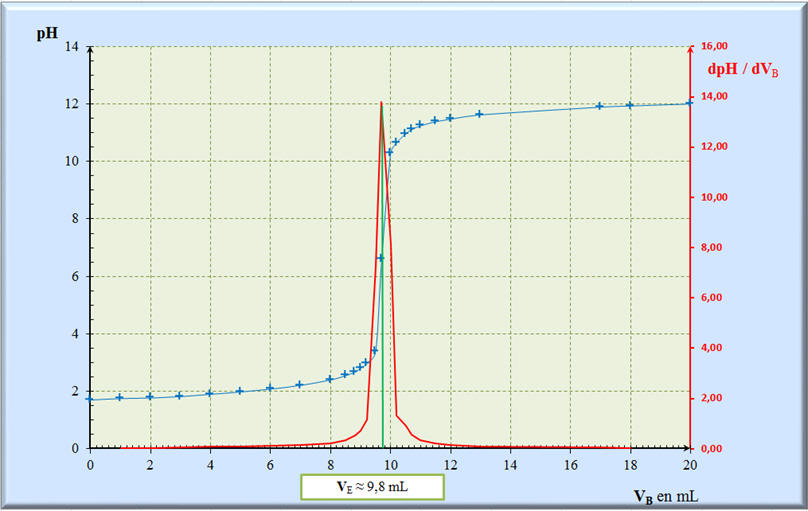
► Graphe
pH
= f (VB) :
► Commentaires :
-
On décompose la représentation
graphique en trois parties :
-
Le
pH
augmente lors de l’addition d’un volume
VB
de soude.
![]() Partie AB de la courbe (partie
jaune) :
Partie AB de la courbe (partie
jaune) :
- Au départ, la valeur du pH est faible. La valeur du pH augmente d’abord lentement car l’acide est en excès par rapport à la base.
- La base est le
réactif limitant.
![]() Partie
BC de la courbe (partie
verte):
Partie
BC de la courbe (partie
verte):
-
La valeur du
pH
augmente d’autant plus que l’excès d’acide se réduit.
-
On observe un saut de
pH
de plusieurs unités.
- Ce saut de pH provient du changement de réactif limitant.
-
On est aux alentours
de l’équivalence.
-
Dans la partie
BC,
la courbe change de concavité, elle possède un point d’inflexion
E.
-
Ce point particulier est appelé
point d’équivalence, noté
E.
- En ce point, on change de réactif limitant.
- On passe d’un excès d’acide à un excès de base.
![]() Partie
CD de la courbe (partie
bleue) :
Partie
CD de la courbe (partie
bleue) :
-
Dans cette zone, l’acide est le
réactif limitant et la base est le réactif en excès.
- Cet excès impose un pH dont la valeur est élevée.
-
Le
pH
augmente à nouveau lentement puis se stabilise.
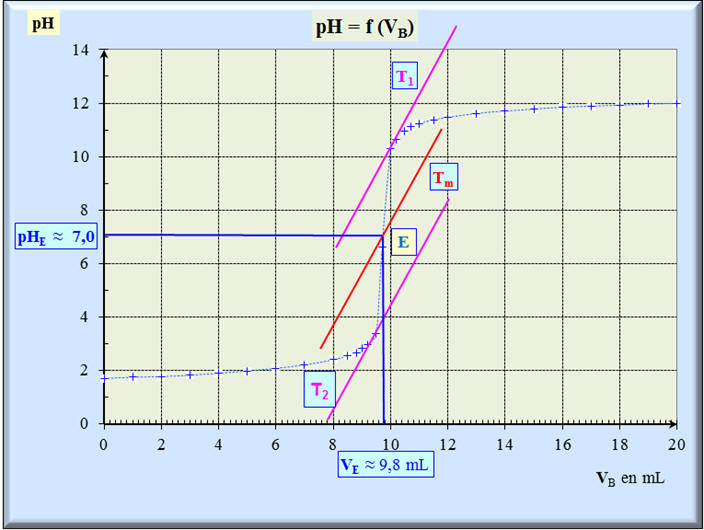
► Détermination graphique du point
d’équivalence E
:
- Le
point d’équivalence est le point d’inflexion de la courbe
pH
= f (V
B).
- On utilise la méthode
des tangentes ou la fonction dérivée
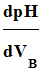 pour déterminer ses
coordonnées.
pour déterminer ses
coordonnées.
- Au point d’équivalence, on change
de réactif limitant et la courbe change de concavité.
- Le point d’équivalence est
caractérisé par ses coordonnées :
pH E et
VBE.
|
- On trace deux tangentes à la courbe pH = f (VB), parallèles et situées de part et d'autre du point d'équivalence (point d'inflexion de la courbe) et suffisamment proche de
l'équivalence. - On trace ensuite la parallèle à
ces deux tangentes, équidistantes de celles-ci. - Son point d'intersection avec la
courbe définit le point d'équivalence
E. - La méthode des tangentes donne
les résultats suivants : |
- Coordonnées du point
d’équivalence E :
- Valeur du pH à
l’équivalence :
pHE = 7,0 à 25 °C
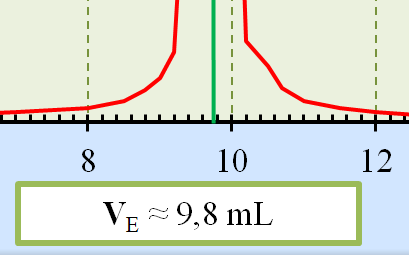
- Volume de soude versée à
l’équivalence :
VE
= 9,8 mL
![]() Méthode de la courbe dérivée :
Méthode de la courbe dérivée :
- À partir des points
expérimentaux, un logiciel de traitement de données permet de
tracer
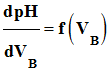 .
.
- On peut faire la représentation
avec le tableur
Excel.
- Tableau de valeurs :
|
VB
mL |
pH |
dpH / dVB |
|
0,0 |
1,7 |
|
|
1,0 |
1,75 |
0,04 |
|
2,0 |
1,77 |
0,04 |
|
3,0 |
1,82 |
0,06 |
|
4,0 |
1,9 |
0,08 |
|
5,0 |
1,98 |
0,09 |
|
6,0 |
2,08 |
0,12 |
|
7,0 |
2,21 |
0,16 |
|
8,0 |
2,4 |
0,23 |
|
8,5 |
2,55 |
0,34 |
|
8,8 |
2,67 |
0,52 |
|
9,0 |
2,81 |
0,73 |
|
9,2 |
2,96 |
1,16 |
|
9,5 |
3,39 |
7,28 |
|
9,7 |
6,6 |
13,80 |
|
10,0 |
10,29 |
8,10 |
|
10,2 |
10,65 |
1,34 |
|
10,5 |
10,96 |
0,92 |
|
10,7 |
11,11 |
0,56 |
|
11,0 |
11,24 |
0,34 |
|
11,5 |
11,38 |
0,23 |
|
12,0 |
11,47 |
0,16 |
|
13,0 |
11,62 |
0,08 |
|
17,0 |
11,89 |
0,06 |
|
18,0 |
11,93 |
0,04 |
|
20,0 |
12 |
|
-
Pour calculer les valeurs de la
colonne dpH /
dVB, on utilise la
relation suivante :
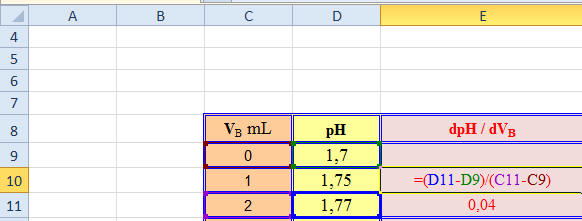
- Puis on recopie cette relation
vers le bas autant que nécessaire.
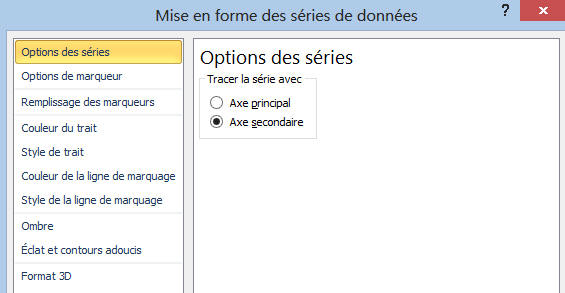
- Pour faire apparaître l’axe
vertical à gauche, on sélectionne la série
dpH /
dVB,
- On fait un clic gauche pour faire
apparaître la fenêtre suivante :
- On clique sur
Mettre en forme une série de
données, puis on sélectionne
Axe secondaire.
- Il ne reste plus qu’à mettre
l’axe en forme.
► Concentration de la solution
d’acide chlorhydrique :
-
À l’équivalence, les réactifs ont
été mélangés dans les proportions stœchiométriques :
|
Équation de titrage |
H3O+
(aq) |
+
HO–
(aq) |
→ |
2
H2O
(ℓ) |
|
|
Quantités de
matières à l’équivalence |
CA
. VA |
CB
. VE |
|
|
|
|
Coefficients
stœchiométriques |
1 |
1 |
|
|
|
|
Relation |
|
|
|
|
|
- 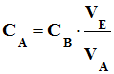
- Application numérique :
-
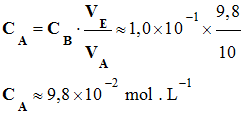
3)- Cas
d’un dosage colorimétrique.
-
Lors d’un titrage colorimétrique,
un changement de teinte du mélange réactionnel permet de repérer
l’équivalence.
-
Ce repérage peut être facilité
par l’utilisation d’un indicateur de fin de réaction.
b)-
Exemple : titrage colorimétrique
du diiode par une solution de thiosulfate de sodium.
► But de la manipulation :
- On veut déterminer la valeur de la concentration C1 d'une solution S1de diiode {I2 (aq)}
-
à partir d'une solution S2
de thiosulfate de sodium {2 Na+ (aq) +
SO32–
(aq)} de concentration C2 = 4,0
x 10–2 mol . L–1.
-
On utilise un indicateur coloré
(l'empois d'amidon) qui permet de repérer l'équivalence.
|
► Dispositif expérimental : - Dans une burette graduée de 25 mL, on introduit la solution S2 de thiosulfate de sodium de concentration C2 = 4,0 × 10–2 mol . L–1
et on règle le zéro
de la graduation. - Grâce à une pipette jaugée, on
prélève un volume V1 = 10 mL de solution
S1 de
diiode {I2 (aq)}. - On verse le contenu de la pipette
dans un erlenmeyer de 250 mL et on ajoute un volume
V0 = 50 mL
d’eau distillée. - Au départ, la solution a la
teinte suivante :
- On verse progressivement la
solution de thiosulfate de sodium (contenue dans la burette
graduée) dans l’erlenmeyer, tout en agitant. - La solution de
S1
de diiode {I2 (aq)} se décolore
progressivement. - Pour que l'indicateur qui permet de repérer l'équivalence soit performant, il faut en verser quelques gouttes juste avant l'équivalence lorsque la solution est jaune paille (on peut faire plusieurs dosages pour améliorer
la technique). - Teinte du mélange réactionnel
avant l’ajout de l’empois d’amidon :
- Après l’ajout de l’empois
d’amidon, le mélange réactionnel prend une teinte
bleue-violacée.
- À l’équivalence, le mélange
réactionnel prend la teinte suivante :
|
-
Le volume de solution
S2
de thiosulfate de sodium est : VE = 12,5 mL.

►
Équation de la réaction de
titrage :
I2 (aq)
+ 2 S2O32–
(aq) → 2
I– (aq)
+
S4O62–
(aq)
►
Tableau d’avancement de la
réaction :
|
Équation |
I2
(aq) + |
2 S2O32–
(aq) |
→ |
2 I–
(aq) |
+ S4O62–
(aq) |
|
|
état |
Avancement
x
(mol) |
n
(I2) |
n
(S2O32–) |
|
n
(I–) |
n
(S4O62–) |
|
État initial à
l’équivalence
(mol) |
0 |
n
(I2)
= C1 . V1 |
n
(S2O32–)
= C2 . VE |
|
0 |
0 |
|
Au cours de la
transformation |
x |
C1
. V1 – x |
n
(S2O32–)
– 2 x |
2 x |
x |
|
|
État final à
Équivalence |
xmax
= xE |
C1
. V1 – xE |
n
(S2O32–)
– 2 xE |
2 xmax |
xmax |
|
|
0 |
0 |
|
|
|
||
|
C1
. V1 = xE |
C2
. VE = 2 xE |
|
2 xmax |
xmax |
||
►
Concentration de la solution
S1 de
diiode :
-
À l’équivalence, les réactifs ont
été mélangés dans les proportions stœchiométriques :
|
Équation de titrage |
I2
(aq) |
+
2
S2O32–
(aq) |
→ |
2
I–
(aq) +
S4O62–
(aq) |
|
|
Quantités de
matières à l’équivalence |
C1
. V1 |
C2
. VE |
|
|
|
|
Coefficients stœchiométriques |
1 |
2 |
|
|
|
|
Relation |
|
|
|
|
|
-
![]()
-
Application numérique :
- 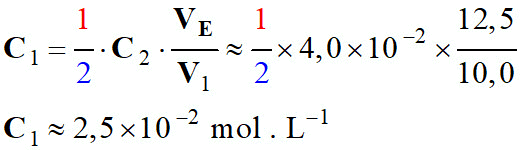
c)-
Les indicateurs colorés
acido-basiques.
- Ce sont des indicateurs dont la teinte dépend du pH de la solution.
-
Ils possèdent une zone de virage.
|
|
3,1 |
4,4 |
||
|
Hélianthine |
rouge |
Zone de Virage
orange |
Jaune |
|
|
|
6,0 |
7,6 |
||
|
B.B.T |
jaune |
Zone de Virage
vert |
Bleu |
|
|
|
8,2 |
10 |
||
|
Phénolphtaléine |
Incolore |
Zone de virage Rose
très pâle |
Rose |
|
-
Un indicateur coloré convient
pour un dosage acido-basique si sa zone de virage contient la
valeur du
pH
du mélange réactionnel à l’équivalence.
-
L’indicateur est convenablement
choisi si l’ajout d’une seule goutte de solution titrante
s’accompagne à la fois du passage par l’équivalence et d’un
changement de couleur de l’indicateur.
-
Les indicateurs colorés sont
constitués par des couples acide faible / base faible dont les
espèces conjuguées ont des teintes différentes.
-
Écriture symbolique :
-
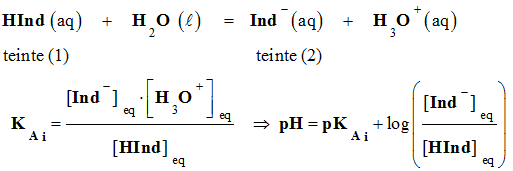
-
On admet, de façon générale, que
l'indicateur coloré prend sa teinte acide si :
-
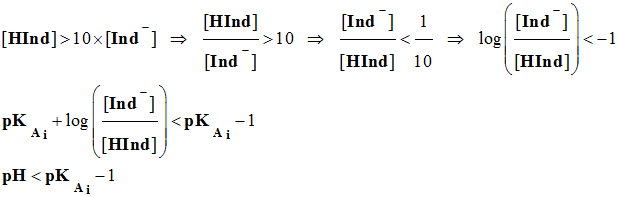
-
On admet, de façon générale, que
l'indicateur prend sa teinte basique si :
-
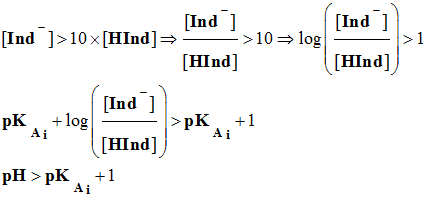
-
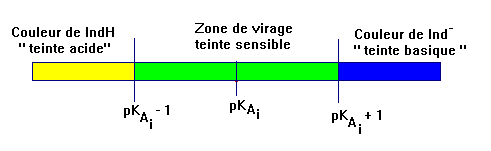
Dans la zone de
pH,
comprise entre pKAi – 1
≤ pH
≤ pKAi
+ 1, l’indicateur coloré prend sa teinte sensible.
-
Les couleurs des teintes acide et
basique se superposent. Cette zone est appelée zone de virage de
l’indicateur coloré.
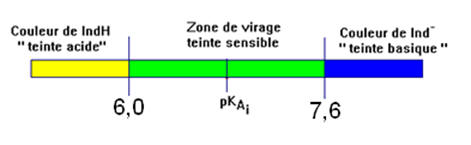
►
Exemple : B.B.T. (Bleu de
bromothymol)
-
Domaine de prédominance : zone de
virage : 6,0 - 7,6.
-
Remarque :
- La zone de virage est inférieure à 2 unités pH car la teinte acide est jaune et la teinte basique est bleue.
-
L’œil peut bien distinguer les deux couleurs.
-
Il se peut que la zone de virage
soit supérieure à 2 unités pH si l’œil a du mal à
distinguer les deux couleurs.
4)-
Expression du résultat d’un titrage.
► Un titrage doit être réalisé avec
le plus grand soin.
► Les sources d’erreurs possibles
sont les suivantes :
- Incertitudes liées aux manipulations :
- mauvais ajustement des niveaux lors du pipetage,
- mauvaise lecture du volume VE sur la burette
graduée (erreur de parallaxe), …
- Incertitudes liées à la méthode de titrage employée :
- imprécisions des méthodes graphiques,
- imprécisions de la valeur de la concentration de la solution
titrante, …
- Incertitudes liées à la verrerie :
- tolérance de ± 0,02 mL pour une pipette jaugée,
- tolérance de
± 0,05 mL pour une burette graduée, …
-
En conséquence :
|
La concentration de la solution
titrée est déterminée avec un intervalle de confiance |
2)-
Exercices :
a)-
Exercice 6 page 478 : Utiliser la
loi de Beer-Lambert.
b)-
Exercice 7 page 478 : Utiliser la
loi de Kohlrausch.
c)-
Exercice 8 page 478 : Utiliser
une relation d’équivalence.
d)-
Exercice 14 page 480 : Choisir un
indicateur coloré.
e)-
Exercice 16 page 481 : Titrage
colorimétrique d’une eau oxygénée.
f)-
Exercice 18 page 481 : Retrouver
la loi de Kohlrausch.
g)-
Exercice 21 page 483 :
Chaufferette chimique.
h)-
Exercice 24 page 485 : Titrage de
l’acide lactique dans le lait.
|
|