I- Les dosages par étalonnage.

1)- Définitions.

2)- Exemples : les différents types de dosages :

-  Dosage avec un spectrophotomètre.

-  Dosage avec un conductimètre (titrage conductimétrique).

-  Dosage avec un pH-mètre (titrage pH-métrique).

-  Dosage avec un indicateur coloré (titrage colorimétrique).

II- Dosage spectrophotométrique.

1)- Le spectrophotomètre.

a)-  Mesure de l’absorbance d’une solution par spectrophotométrie.

-  On utilise le fait que toute solution colorée absorbe la lumière visible (400 nm < λ₀ < 800 nm).

-  Lorsqu’un faisceau de lumière monochromatique traverse un milieu absorbant, l’intensité lumineuse I du faisceau transmis est inférieure à l’intensité lumineuse I₀ du faisceau incident.

-  Pour évaluer cette diminution, on utilise :

-  La transmittance T :

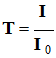
-  L’absorbance A :

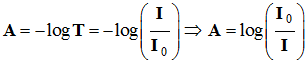
-  La transmittance s’exprime en pourcentage.

-  À une transmittance T de 100 % (T = 1) correspond une absorbance nulle : A = 0.

-  à une transmittance de 1 % (T = 0,01) correspond une absorbance A = log 100 = 2.

-  Exemple de réaction :

-  On peut utiliser cette méthode lorsqu’une espèce colorée se forme ou disparaît au cours de la réaction.

-  Réaction entre l’eau oxygénée et les ions iodure en milieu acide :

-  Il se forme du diiode qui est une espèce chimique colorée.

-  Équation de la réaction :

b)-  Principe de fonctionnement.

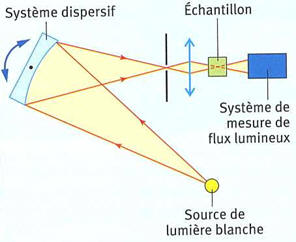
-  Un système dispersif (prisme ou réseau) permet de sélectionner une radiation lumineuse de longueur d’onde λ donnée.

-  Cette radiation est dirigée vers l’échantillon à analyser.

-  Le flux lumineux transmis est mesuré et converti en valeur d’absorbance A.

c)-  Absorbance en fonction de la longueur d’onde.

-  L’absorbance d’une solution colorée dépend de la longueur d’onde de la radiation lumineuse utilisée.

-  On donne l’absorbance d’une solution de diiode en fonction de la longueur d’onde :

-  Pour une solution de diiode de concentration C = 1,0 mmol / L, on mesure l’absorbance A pour différentes longueurs d’ondes.

-  La plage de variation de la longueur d’onde se situe dans l’intervalle suivant :

-   400 nm < λ < 700 nm.

-  On règle la longueur d’onde sur la valeur souhaitée, on fait le blanc avec la solution étalon, puis on mesure l’absorbance.

-  Il faut répéter le mode opératoire pour chaque mesure.

-  Courbe obtenue :

2)- Absorbance en fonction de la concentration.

a)-  Réglage du spectrophotomètre.

-  Pour réaliser les mesures d’absorbance, le spectrophotomètre est généralement réglé sur la longueur d’onde λ_max correspondant au maximum d’absorption du spectre de la solution étudiée.

-  À cette longueur d’onde, la valeur de l’absorbance étant la plus grande, l’incertitude sur la mesure est la plus petite.

-  Pour les solutions aqueuses de diiode, on choisit λ = 450 nm, pour avoir le maximum de variations pour la valeur de A.

-  On n’a pas choisi λ = 475 nm car le spectrophotomètre sature en fin d’expérience lorsque la concentration en diiode devient trop grande.

b)-  Préparation des solutions et mesures :

-  On dispose d’une solution S₀ de concentration en diiode C₀ = 1,0 mmol / L.

-  À partir de S₀, préparer les solutions 10 mL de solution S en utilisant les solutions présentes dans les burettes.

-  Matériel :

-  Préparer la solution S et réaliser la mesure de l’absorbance de la solution préparée.

-  Pour préparer la solution S, on mélange la solution de diiode de concentration C₀ = 1,0 mmol / L et la solution d’iodure de potassium de concentration C = 0,20 mol / L.

c)-  Exploitation des mesures.

-  On trace la courbe A = f (C).

-  Courbe obtenu par le Groupe 1 :

-  On obtient la courbe d’étalonnage.

-  Ce graphe est une portion de droite passant par l’origine.

-  L’absorbance A est proportionnelle à la concentration C de la solution de diiode.

-  A = k . [I₂].

3)- Loi de Beer-Lambert.

-  On peut généraliser ce résultat à toutes les solutions colorées.

-  Pour les solutions suffisamment diluées, l’absorbance A est proportionnelle à la concentration C de l’espèce colorée.

►  Définition :

-  La courbe A = f (C) constitue la courbe d’étalonnage de la substance étudiée.

-  Elle permet de déterminer la concentration d’une solution de la substance étudiée.

-  Elle permet donc de doser une espèce chimique colorée.

-  Afin d’augmenter la sensibilité de la méthode, on utilise la longueur d’onde qui correspond au maximum d’absorption de la substance étudiée.

-  Cette méthode est alors beaucoup plus précise que la méthode colorimétrique utilisant une échelle des teintes.

-  Remarque : la solution colorée doit être suffisamment diluée, 

-  C ≤ 1,0 × 10^–2 mol . L^–1, et le spectrophotomètre ne doit pas saturer.

III- Dosage conductimétrique.

1)- Le conductimètre.  Titrage conductimétrique

a)-  Présentation :

b)-  Étalonnage :

-  Régler le bouton de température du conductimètre sur la température de la pièce.

-  Rincer (avec de l'eau distillée) et essuyer délicatement (avec du papier Joseph) la sonde.

-  Plonger la sonde dans une solution d'étalonnage.

-  Régler le bouton d'étalonnage du conductimètre pour que la valeur affichée coïncide avec la valeur donnée par le fabriquant de la solution d'étalonnage (à la température de la pièce).

-  Sortir la sonde de la solution d'étalonnage, la rincer, la replacer dans l'eau distillée.

c)-  Réaliser une mesure :

-  Rincer la sonde de conductimétrie (si possible avec la solution dont on veut mesurer la conductivité). L'essuyer délicatement avec du papier Joseph.

-  Plonger la sonde dans la solution dont on veut mesurer la conductivité.

-  Attendre la stabilité (quelques secondes).

-  Lorsque la lecture est terminée, rincer la sonde et la plonger dans la solution d'eau.

2)- Application :

Correction :

3)- Loi de Kohlrausch :

a)-  La conductivité d’une solution ionique (rappels).

-  Cellule conductimétrique :

Mesure de la conductance d’une solution de chlorure de sodium :

►  Dispositif expérimental : Conductance et facteur d’influence..

-  Réglages : On choisit le signal sinusoïdal :

-  On règle la fréquence du G.B.F sur 500 Hz.

-  On règle la tension U aux bornes de la cellule sur 1,00 V.

-  On choisit la cellule conductimétrique :  S = 1 cm² et ℓ  = 1 cm

-  Solution de chlorure de sodium de concentration C = 5,0 × 10^{– 3} mol / L.

►  Mesure :

-  Avant chaque mesure, il faut rincer les électrodes à l’eau distillée.

-  Essuyer délicatement les électrodes avec du papier absorbant, agiter doucement la cellule dans la solution pour bien homogénéiser.

-  La conductance G est proportionnelle à la concentration C de la solution si C < 1,0 ×10^–2 mol / L.

-  G = k’ . C

-  D’autre part :

-  La conductance G d’une portion de solution est proportionnelle au rapport .

-  Par définition, le coefficient de proportionnalité est appelé :

-  Conductivité de la solution ionique que l’on note σ ''sigma minuscule''.

-  On écrit :

-  La grandeur σ est caractéristique de la solution.

-  Elle rend compte de la capacité de la solution à conduire le courant électrique.

-  Elle ne dépend pas de la géométrie de la cellule.

-  La grandeur σ est liée à la nature et la concentration des ions présents dans la solution.

►  La conductance G :

-  La conductance G est l’inverse de la résistance R d’une portion de solution.

-  G dépend de la solution et des caractéristiques géométriques de la cellule de mesure.

-  Pour s’affranchir de ces caractéristiques, on définit la conductivité σ à partir de la conductance :

-  G = k_cellule . σ

-  La grandeur k_cellule est la constante de la cellule.

-  Lorsqu’on réalise un dosage avec un conductimètre, on utilise toujours la même cellule.

-  On réalise toujours un étalonnage de l’appareil avant d’effectuer une série de mesures.

b)-  Conductivité molaire ionique.

-  À chaque ion d’une solution ionique, on affecte une conductivité molaire ionique λ.

-  La conductivité molaire ionique se rapporte à un ion donné.

-  Elle dépend de la température, de la nature du solvant.

-  Elle ne dépend pas de la concentration si  C < 1,0 × 10^–2 mol / L.

-  Exemple pour les ions sodium, on écrit :

-  λ (Na ⁺) = 5,01 × 10^– 3 S . m² . mol^{– 1} dans l’eau.

-  Pour les ions chlorure :

-  λ (Cl^–) = 7,63 × 10 ^{–  3} S . m² . mol^{– 1} dans l’eau.

-  Remarque :

-  Dans une solution électrolytique, ce sont les ions qui sont responsables du passage du courant.

-  Un courant dans une solution est dû à la circulation des ions positifs et négatifs se déplaçant en sens inverse.

-  Chaque ion dans la solution contribue à la conductivité de celle-ci.

-  La conductivité σ de la solution est égale à la somme des conductivités due aux cations et aux anions.

-  On écrit :

-   σ  =  σ (+) + σ (–)

-  Formule générale :

-   

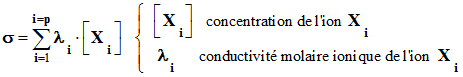
-  La conductivité σ d’une solution ionique dépend de la nature des ions présents X_i et de leur concentration [ X_i ] respectives.

►  Conductivité molaire ionique de quelques ions :

►  Exemple :

-  Pour une solution de chlorure de sodium :

-  Solution de chlorure de sodium :

-  Or : C = [Cℓ^–] = [Na⁺]

-  σ  =  λ (Cℓ^–) . [ Cℓ^– ] + λ (Na⁺) . [ Na⁺ ]

-  σ  =  {λ (Cℓ^–) + λ (Na⁺) } . C

-  Solution de chlorure de baryum :

-  Or : [ Ba²⁺ ] = C et [ Cℓ^– ] = 2 C

-  σ  =  λ (Cℓ^–) . [ Cℓ^– ] + λ (Ba²⁺) . [ Ba²⁺ ]

-  Expression en fonction de C :

-  σ  =  λ (Cℓ^–).2 C + λ (Ba²⁺). C

-  σ  = (2 λ (Cℓ^–).+ λ (Ba²⁺) ) . C

►  Remarque :

-  σ  = k . C

c)-  Énoncé de la loi de Kohlrausch :

-  À partir de la mesure de la conductivité d’une solution, on peut déterminer la valeur de sa concentration.

►  Remarque :

-  On peut le faire aussi à partir de la valeur de la conductance si on ne possède pas de conductimètre.

-  Remarque :

-  Les lois de Beer-Lambert et Kohlrausch ont des équations analogues.

-  La solution colorée doit être suffisamment diluée, C ≤ 1,0 × 10^–2 mol . L^–1, et ne doit contenir qu’un seul soluté ionique.

IV- La détermination d’une quantité de gaz.

1)- Introduction.

-  L’état gazeux est un état dispersé.

-  À l’état microscopique :

-  Les molécules ou les atomes sont éloignés les uns des autres et se déplacent dans toutes les directions de façon désordonnée.

-  Les interactions entre les entités chimiques sont faibles.

-  À l’état gazeux règne le chaos moléculaire

-  L’agitation des molécules constituant un gaz, sous faible pression caractérise son état thermique.

-  L’agitation des molécules qui constituent un gaz est liée à une grandeur macroscopique :

-  la température absolue du gaz, notée T.

-  L’unité de température absolue est le Kelvin : symbole K.

-  La température absolue étant liée à l’agitation des molécules d’un gaz, on ne peut pas refroidir indéfiniment un gaz.

-  Lorsque la température diminue, l’agitation thermique diminue aussi.

-  Lorsque les molécules sont immobiles, il n’y a plus d’agitation thermique et on ne peut plus refroidir : c’est le zéro absolu.

-  En l’absence de toute agitation thermique la température T = 0 K.

-  C’est le zéro absolu où toutes les particules sont immobiles.

-  Au zéro absolu, la température absolue est nulle, la pression est nulle et il n’y a plus d’agitation thermique.

-  La température absolue est une grandeur obligatoirement positive.

-  Relation : l’échelle de température Celsius (température notée θ) se déduit de la température absolue par la relation :

-  T (K) = θ ° C  +  273,15 ou T (K) ≈ θ ° C  +  273

2)- Équation d’état du gaz parfait.

-  Un gaz est dit parfait si la taille de ses entités est négligeable devant la distance qui les sépare et si les interactions entre elles sont négligeables.

-  À basse pression, tous les gaz peuvent être assimilés à des gaz parfaits.

►  Équation d’état du gaz parfait :

-  Pour un gaz réel :

-  P . V ≈ n . R . T si la pression est faible et si la température n’est pas trop basse.

-  Dans les conditions habituelles de température et de pression, l’air (mélange de gaz) se comporte comme un gaz parfait.

►  Application :

-  Les briquets à gaz contiennent du butane liquide (C₄H₁₀).

-  La pesée d’un briquet a donné une masse m = 20,51 g.

-  Grâce à un tuyau souple, de faible section et adapté à l’orifice de sortie du gaz, on recueille par déplacement d’eau un volume V = 1,5 L de butane dans une bouteille en matière plastique.

-  On pèse alors le briquet : sa masse m’ = 16,93 g.

-  Masse molaire du butane M (C₄H₁₀) = 58,1 g . mol^–1.

-  Faire un schéma de l’expérience.

-  Au cours de l’expérience, la pression du gaz recueilli est égale à la pression atmosphérique P = 1020 hPa et sa température θ = 23,0 °C.

-  Calculer la quantité de matière n de gaz qui s’est échappée du briquet à partir du volume de gaz obtenu.

-   

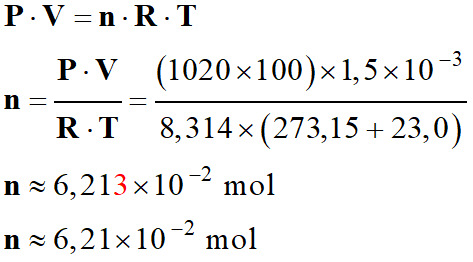
-  Calculer la quantité de matière n de gaz qui s’est échappée du briquet à partir des pesées :

-  m (C₄H₁₀) = m – m’

-   

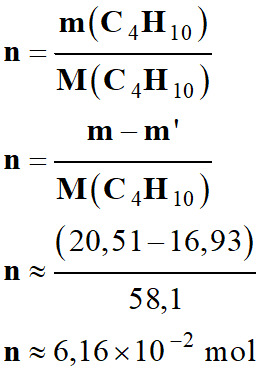
-  Les deux résultats sont cohérents.

-  Volume d’une mole de butane gazeux dans les conditions de l’expérience :

-   

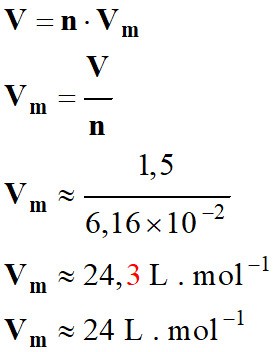
-  Température θ = 23,0 °C.

-  Avec cette expérience simple, on peut avoir une estimation du volume molaire d’un gaz.

3)- Volume molaire et quantité de gaz.

TP le volume molaire

-  Loi d’Avogadro – Ampère :

-  Énoncé :

-  Des volumes égaux de gaz différents, pris dans les mêmes conditions de température et de pression, renferment le même nombre de molécules.

-  Il découle de cette loi que des volumes égaux de gaz différents, pris dans les mêmes conditions de température et de pression, renferment le même nombre de moles.

-  Ainsi :

-  Une mole de dihydrogène, une mole de butane, une mole de méthane occupent le même volume dans les mêmes conditions de température et de pression.

-  Tous les gaz ont le même volume molaire.

-  Le volume molaire :

-  Autre relation :

-  Le volume molaire V_m permet de relier la quantité de gaz n à son volume V.

-  V = n . V_m

V- La spectroscopie.

1)- Groupes caractéristiques et fonctions.

Groupe caractéristique	Famille de composés	Formule générale
– OH Hydroxyle	Alcool	R – OH
Carbonyle	aldéhyde
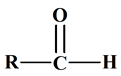	Cétone
carboxyle	Acide carboxylique
groupe ester	Ester
double liaison carbone-carbone	Alcène
groupe amine	Amine (Primaire)
groupe amide	Amide

2)- Spectroscopie UV-visible.

-  Les solutions colorées absorbent certaines radiations dans le domaine du visible, dont la longueur d’onde est comprise entre :

-  400 nm ≤ λ ≤ 800 nm

-  Les solutions incolores peuvent absorber des radiations dans le domaine ultraviolet :

-  Pour une espèce chimique colorée, on peut tracer le graphe donnant l’absorbance A en fonction de la longueur d’onde λ.

-  On obtient alors le spectre d’absorption de l’espèce chimique.

-  Exemple : Spectre d’absorption du diiode :

-  La valeur de la longueur d’onde correspondant à l’absorbance maximale du spectre d’absorption peut permettre l’identification d’une espèce chimique.

3)- Spectroscopie infrarouge IR .

a)-  Présentation d’un spectre. (tsch042010)

-  La spectroscopie IR est une spectroscopie d’absorption.

-  Les composés organiques absorbent aussi dans le domaine de l’infrarouge.

-  Pour ces spectres, on fait figurer :

-  La transmittance T ou intensité lumineuse transmise par l’échantillon analysé en ordonnée (elle s’exprime en pourcentage)

-  Le nombre d’ondes σ en abscisse.

-  Le nombre d’ondes σ est l’inverse de la longueur d’onde λ.

-   

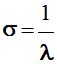
-  Unité :

-  Généralement, le nombre d’ondes σ s’exprime en cm^–1 en chimie organique.

-  En chimie organique, les radiations infrarouges exploitées vont de 400 cm^–1 à 4000 cm^–1. (25 μm à 250 μm)

-  Cette spectroscopie peut se faire en phase gazeuse ou en phase condensée.

-  Exemple : Spectre de la propanone.

-  Remarque :

-  Une faible valeur de transmittance correspond à une forte absorption.

-  Les bandes d’absorption sont orientées vers le bas.

-  L’axe des abscisses est orienté vers la gauche. Cette échelle n’est pas toujours linéaire.

-  On distingue deux zones principales dans le spectre IR :

►  Le nombre d’onde compris entre 1500 et 4000 cm^–1.

-  Cette zone ne contient qu’un nombre limité de bandes, correspondant à des types de liaisons particuliers.

-  Chaque bande est caractérisée par :

-  Sa position dans le spectre (la valeur du nombre d’onde du minimum de transmittance,

-  Sa largeur (bande large ou fine),

-  Son intensité (faible, moyenne ou forte), correspondant à la valeur minimale de la transmittance.

►  Le nombre d’onde compris entre 400 et 1500 cm^–1.

-  Il s’agit d’une zone très riche en bandes d’absorption pour les molécules organiques possédant un ou plusieurs atomes de carbone.

-  Elle est généralement exploitée qu’en comparaison avec un spectre de référence.

-  Cette zone s’appelle l’empreinte digitale de la molécule.

-  Dans un spectre infrarouge, la zone d’identification des groupes caractéristiques correspond à : σ > 1600 cm^–1.

b)-  Utilité :

-  Les spectres IR sont constitués d’une série de bandes d’absorption.

-  Chaque bande d’absorption est associée à un type de liaison, principalement caractérisé par les deux atomes liés et la multiplicité de la liaison.

-  Un spectre infrarouge renseigne sur la nature des liaisons présentes dans une molécule.

-  Les bandes d’absorption associées à chacune des liaisons rencontrées en chimie organique correspondent à un domaine de nombre d’ondes bien précis.

-  Une table des absorptions caractéristiques des liaisons dans le domaine de l’IR donne les fourchettes des nombres d’onde (souvent l’allure des bandes) pour différents types de liaison.

-  Un spectre infrarouge nous renseigne sur la nature des liaisons présentes dans la molécule et permet d’en identifier les groupes caractéristiques.

c)-  Origine du spectre :

-  Les spectres IR sont liés au fait que les atomes d’une molécule ne sont pas fixes, ils vibrent autour d’une position d’équilibre.

-  Les vibrations peuvent correspondre à une élongation longitudinale :

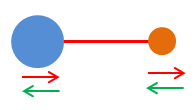
-  Les vibrations peuvent correspondre à une déformation angulaire :

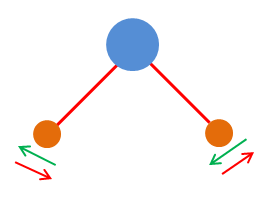
-  Les vibrations des liaisons d’une molécule sont à l’origine de son spectre infrarouge.

-  Un spectre infrarouge renseigne sur la nature des liaisons présentes dans une molécule et sur les groupes caractéristiques qui sont présents dans la molécule.

d)-  Bandes d’absorption caractéristiques.

-  Tableau simplifié :

-  Les notations :

-  L’intensité traduit l’importance de l’absorption.

-  – O – H_lib sans liaison hydrogène et – O – H_lié avec liaison hydrogène.

-  C_tri correspond à un carbone trigonal engagé dans une double liaison.

-  C_têt correspond à un carbone tétragonal engagé dans quatre liaisons simples.

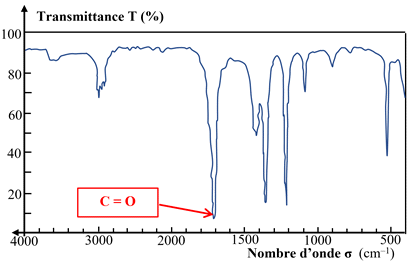
►  Bande C = O

-  La liaison C = O est présente dans de nombreuses molécules organiques telles que les aldéhydes, cétones, acide carboxyliques, esters, amides,…

-  La position de la bande d’absorption dépend de la nature de la fonction.

-  Elle est généralement comprise entre 1650 cm^–1 et 1750 cm^–1.

-  Lorsque la liaison C = O est conjuguée à d’autres doubles liaisons, la liaison C = O est affaiblie et le nombre d’onde correspondant diminue.

►  Bande C – O 

-  La liaison C – O est présente dans les alcools, les acides carboxyliques,…

-  Sa bande d’absorption se situe entre 1070 cm^–1 et 1450 cm^–1.

-  Tableau à connaître :

-  Une bande est forte lorsque la valeur de la transmittance est faible.

-  Une bande est large si elle s’étale sur un intervalle de nombre d’ondes important.

-  En résumé :

Groupe hydroxyle :

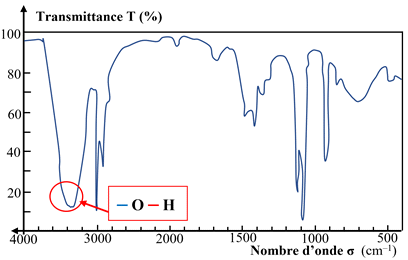
Groupe carbonyle :

Groupe carboxyle :

e)-  Exemples de spectres infrarouges :

►  Spectre IR de l’éthanol :

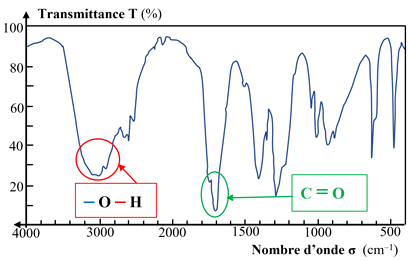
-  Spectre de l’éthanol à l’état gazeux :

-  Spectre de l’éthanol à l’état liquide :

-  Ci-dessus, on peut observer les spectres infrarouges de l’éthanol à l’état gazeux et à l’état liquide.

-  À l’état gazeux :

-  La liaison O – H donne une bande moyenne et fine vers 3620 cm^–1.

-  Il n’existe pas de liaison hydrogène entre les molécules d’éthanol, la liaison O – H est dite libre.

-  On la note O – H_lib.

-  À l’état liquide :

-  La liaison O – H se manifeste par une bande d’absorption forte et large de 3200 cm^–1 à 3400 cm^–1.

-  Les liaisons hydrogène établies entre les molécules d’éthanol affaiblissent les liaisons covalentes O – H et conduisent à un abaissement du nombre d’onde σ_{O – H}.

-  De plus, la bande s’élargit. La liaison O – H est dans ce cas dite associée, on la note O – H_associé ou O – H_lié.

-  Ce résultat est général.

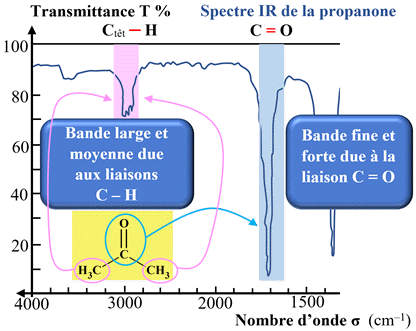
►  Cas de la propanone :

-  Les liaisons C – H donnent une bande large et moyenne de 2800 cm^–1 à 3100 cm^–1.

-  La double liaison C = O donne une bande fine et forte vers 1700 cm^–1.

►  Acide éthanoïque :

-  Les liaisons O – H donnent une bande large et forte de 2500 cm^–1 à 3200 cm^–1.

-  Pour les acides carboxyliques en solution concentrée, les molécules s’associent sous forme de dimères grâce à des liaisons hydrogène.

-  On note un affaiblissement important des liaisons – O – H.

-  La bande d’absorption relative aux liaisons – O – H se situe autour du nombre d’onde σ ≈ 3000 cm^–1.

-  Cette bande est caractéristique d’un acide carboxylique.

-  La double liaison C = O donne une bande fine et forte vers 1700 cm^–1.

►  Comparaison du spectre IR du propanal avec celui de la propanone.

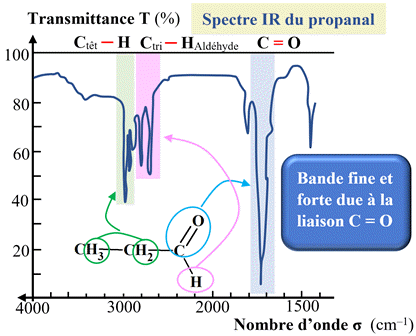
- Dans ce cas on travaille sur la partie comprise entre 1500 cm^–1 et 4000 cm^–1.

- Les deux spectres présentent une bande forte et fine centrée sur 1700 cm^–1.

- Cette bande est caractéristique du groupe carbonyle C = O.

- Dans le spectre IR du propanal, on remarque la présence de deux bandes moyennes et fines entre 2750 cm^–1 et 2900 cm^–1, caractéristiques de la liaison C_tri – H_Aldéhyde.

- Ces deux bandes ne sont pas présentes dans le spectre de la propanone.

- Ces deux bandes permettent de distinguer la molécule de propanal de la molécule de propanone.

VI- Applications.

1)- Dosage par étalonnage conductimétrique.

-  Évolution de la conductivité lors d’un titrage.

-  Dosage des ions chlorure dans le lait.

2)- QCM.

Méthodes d’analyse physique

Les dosages par étalonnage

La détermination d’une quantité de gaz

La spectroscopie

 QCM réalisé avec le logiciel Questy

Pour s'auto-évaluer

Sous forme de tableau

3)- Exercices.