Chap. N° 15 Premier principe de la thermodynamique et bilan énergétique

- Les grandeurs macroscopiques de description du gaz
(température T , pression P , masse volumique ρ )
reflètent le comportement microscopique des entités chimiques
(atomes, molécules ou ions) qui le constituent.

b)- Le gaz parfait :

- Un gaz est dit parfait si la taille de ses entités est négligeable devant la distance qui les sépare et si les interactions entre elles sont négligeables.

- À basse pression, tous les gaz peuvent être assimilés à des gaz parfaits.

GAZ PARFAIT

À l’échelle macroscopique

Grandeur physique

À l’échelle microscopique

Comportement

Le gaz parfait est au repos

à la température T (K)

Mouvement incessant et

désordonné des entités du gaz

Pas d’interaction entre

les entités assimilées à des

points matériels

La pression P (Pa) est faible

Pas de chocs entre les entités de gaz

Chocs seulement entre les entités

du gaz et la paroi

La masse volumique

(kg . m^–3) est très faible

Les entités du gaz sont éloignées

les unes des autres.

c)- Équation d’état du gaz parfait :

- Cette équation relie les différentes grandeurs macroscopiques qui permettent de le décrire.

P . V = n . R . T
P	Pression en pascal (Pa)
V	Volume en mètre cube (m³)
n	Quantité de matière en mole (mol)
R	Constante des gaz parfaits : R = 8,314 Pa . m³ .mol^–1 . K^–1
T	Température absolue en kelvin (K)

► Volume du gaz parfait :

► Masse volumique du gaz parfait :

- masse volumique du gaz parfait

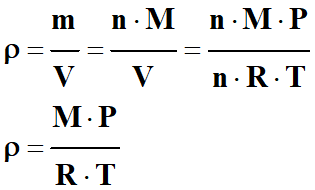
2)- Quelques limites du modèle du gaz parfait.

- Si la pression et la masse volumique du gaz sont trop importantes, alors le modèle du gaz parfait n’est plus adapté.

- Le modèle du gaz parfait est adapté :

- Si la pression est faible ;

- Si l’entité chimique qui constitue le gaz est de faibles dimensions

- Pour un gaz réel :

- P . V ≈ n . R . T si la pression est faible et si la température n’est pas trop basse.

- Dans les conditions habituelles de température et de pression, l’air (mélange de gaz) se comporte comme un gaz parfait.

II- L’énergie interne et les modes de transfert de l’énergie.

1)- Énergie interne U d’un système.

► Échelle microscopique :

- À l'échelle microscopique, les particules constituant le système sont animées de mouvements individuels.

- L’énergie cinétique microscopique est lié à la vitesse de déplacement des particules du système dans le référentiel d’étude.

- Cette agitation augmente avec la température T, on l'appelle l'agitation thermique.

- Plus la température d’un système est élevée, plus l’agitation thermique des particules qui le constituent est grande et plus son énergie cinétique microscopique est grande.

- Au niveau microscopique, à toute liaison entre deux particules du système est associée une énergie potentielle microscopique.

- L’énergie potentielle microscopique est due aux interactions gravitationnelle, électromagnétique, forte et faible entre les particules qui constituent le système.

- On distingue les énergies potentielles microscopiques chimique, électrique, magnétique et nucléaire.

- Les énergies potentielles résultent de l’énergie de liaisons chimiques et de l’énergie de masse des noyaux.

- On peut citer d’autres formes d’énergies potentielles microscopiques qui résultent de liaisons intermoléculaires entre les molécules qui constituent le système étudié.

- Ces énergies potentielles microscopiques varient lors d’un changement d’état de la matière : fusion, liquéfaction, solidification.

- L’énergie interne est la somme des énergies cinétique et potentielle microscopiques, c’est l'énergie liée à sa structure interne microscopique, notée U.

- Énergie interne : U (J)

- Le plus souvent, on s’intéresse à la variation de l’énergie interne ΔU d’un système.

2)- Énergie totale d’un système.

► Échelle macroscopique :

- L’énergie mécanique E_m d’un système macroscopique résulte de contributions macroscopiques.

- L’énergie mécanique d’un système est la somme de son énergie cinétique et de son énergie potentielle.

- Relation :

- E_m = E_C + E_P.

- Unité : joule (J)

► Énergie totale d’un système :

- L’énergie totale d’un système est la somme de son énergie interne U et de son énergie mécanique E_m.

- E_tot = E_m + U

- La variation d’énergie totale d’un système est égale à la somme des variations de son énergie interne et de son énergie mécanique :

- ΔE_tot = ΔE_m + ΔU

► Système au repos macroscopique :

- Lorsqu’un système est au repos macroscopique dans le référentiel d’étude, son énergie mécanique est constante.

- La variation d’énergie totale du système est alors égale à sa variation d’énergie interne :

- ΔE_tot = ΔU

3)- Deux modes de transfert de l’énergie.

Transferts macroscopique d'énergie

a)- Le travail W.

- Exemple :

- Un transfert d'énergie ayant pour effet de modifier la position, la forme d'un objet ou

de le mettre en mouvement par rapport à un référentiel donné est appelé travail mécanique noté W_m.

- On parle plus simplement de travail noté W exprimé en Joule (J).

- Le travail W est un transfert d’énergie qui s’effectue macroscopiquement de façon ordonnée.

- Il peut être lié au déplacement du point d’application d’une force s’exerçant sur un système.

Transferts d'énergie et conservation

b)- Le transfert thermique Q.

Transferts d'énergie et énergie interne

- La thermodynamique étudie plus particulièrement les transformations de transfert thermique en travail et réciproquement.

- Le transfert thermique est de l'énergie cinétique d'agitation des particules qui composent le système ; mais cette agitation est désordonnée.

- La différence entre transfert thermique et travail est expliquée par la mécanique statistique ;

celle-ci permet de définir une fonction qui mesure le degré de "désordre" d'un état macroscopique d'un système.

- Cette fonction s'appelle l'entropie.

- Le transfert thermique est une forme d'énergie.

- Le transfert thermique Q est un transfert d’énergie qui s’effectue microscopiquement de manière désordonnée entre le système et le milieu extérieur.

- Le milieu extérieur est tout ce qui n’est pas le système.

- Ainsi, lorsqu’il existe une différence de température entre le système et le milieu extérieur,

le transfert thermique Q se fait spontanément du corps le plus chaud vers le corps le plus froid.

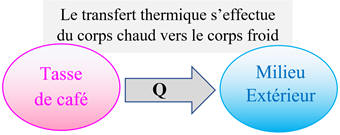
► Exemple : La tasse de café :

- Cas d’une tasse de café (65 ° C) qu’on laisse à la température ambiante (21 ° C).

- Au cours du temps, la température du café diminue.

- La tasse de café constitue le système d’étude S , l’autre système S’ est constitué par le milieu extérieur.

- Un transfert d’énergie s’effectue de la tasse de café vers le milieu extérieur.

- La tasse de café cède de l’énergie sous forme de transfert thermique, notée Q, au milieu extérieur.

transferts d'énergie

- Un transfert thermique a pour conséquence macroscopique une modification de la température T ou un changement d’état physique du système.

c)- Travail et transfert thermique :

- Le travail W et le transfert thermique Q sont des grandeurs algébriques.

- Par convention :

- Le travail W et le transfert thermique Q sont comptés positivement s’ils sont reçus par le système.

- Le travail W et le transfert thermique Q sont comptés négativement s’ils sont cédés par le système.

- Le bilan énergétique dépend du système choisi.

- Avant tout bilan, il faut préciser le système d’étude.

- L’énergie d’un système varie s’il reçoit ou cède de l’énergie.

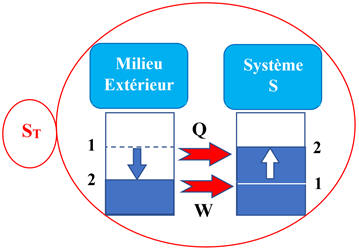
Travail et transfert thermique

- On peut écrire que :

- ΔE_S = E₂ – E₁ = Q + W

► Exemple de convertisseurs d’énergie.

- Le radiateur électrique convertit de l’énergie électrique en énergie thermique.

- Le système (Radiateur électrique) reçoit un travail électrique : W > 0

- Le système (Radiateur électrique) cède un transfert thermique : Q < 0

► La bouilloire électrique :

Transferts d'énergie dans un circuit électrique

- Une bouilloire électrique, alimentée par la tension du secteur de valeur efficace U_eff = 230 V.

- Elle comprend un conducteur ohmique de résistance R = 120 Ω.

Bouilloire résistance incandescente

- On verse 500 mL d’eau dans la bouilloire électrique que l’on chauffe à 60 ° C.

- Le système étudié est le conducteur ohmique de la bouilloire.

- Le conducteur ohmique est alimenté par une source de tension.

- Il reçoit de l’énergie sous forme de travail électrique W compté positivement.

- D’autre part, il cède de l’énergie à l’eau qui constitue le milieu extérieur sous forme de transfert thermique Q.

- Ce transfert thermique Q est compté négativement pour le conducteur ohmique.

► Chaîne énergétique :

III- Le premier principe de la thermodynamique.

1)- Énoncé :

- La variation ΔU_i→fd’énergie interne d’un système,

- Qui n’échange pas de matière avec le milieu extérieur,

- Au repos macroscopique,

- Qui évolue d’un état initial (i) à un état final (f)

- Est égale à la somme des énergies échangées par le système avec le milieu extérieur,

- Par travail W et / ou par transfert thermique Q :

ΔU_i→f = W + Q

ΔU_i→f : Variation d’énergie interne (joule : J)

W : Travail (électrique ou mécanique) (joule : J)

Q : Transfert thermique (joule : J)

- Remarques :

- L’énergie mécanique d’un système au repos macroscopique dans le référentiel d’étude est constante.

- Le premier principe de la thermodynamique relie la variation d’énergie interne aux transferts d’énergie.

- Il permet d’établir le bilan énergétique d’un système qui n’échange pas de matière avec le milieu extérieur.

2)- Étude énergétique d’un système thermodynamique.

► Établissement d’un bilan énergétique :

- Il faut :

- Définir le système au repos macroscopique, l’extérieur est alors le reste de l’Univers ;

- Écrire le premier principe de la thermodynamique ;

- Relever tous les transferts d’énergie ayant lieu entre le système et le milieu extérieur

- Repérer le sens de chaque transfert d’énergie ;

- Attribuer un signe positif si l’énergie est reçue par le système ;

- Attribuer un signe négatif si l’énergie est cédée par le système ;

- Effectuer la somme de tous ces transferts :

- Si la somme est positive, l’énergie interne du système a augmenté ;

- Si la somme est négative, l’énergie interne du système a diminué.

► Application :

- Le fluide frigorigène d’une pompe à chaleur prend de l’énergie à l’air froid extérieur et en transfère à l’air de la pièce à chauffer.

- Pour cela, un compresseur transfère de l’énergie par travail mécanique au fluide frigorigène.

- Schéma du dispositif :

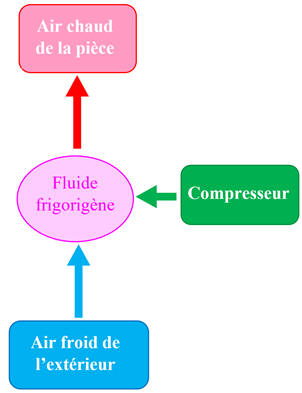
fluide frigorigène

- Compléter le schéma avec les trois transferts d’énergie ayant lieu entre le système (fluide frigorigène) et le milieu extérieur.

- Écrire le premier principe pour le système (fluide frigorigène).

► Réponses :

- Schéma légendé :

fluide frigorigène

- Premier principe pour le système (fluide frigorigène) :

- Système étudié : Fluide frigorigène

- W : Énergie reçue sous forme de travail mécanique W > 0 J

- Q₁ : Transfert thermique reçu du milieu extérieur : Q₁ > 0 J

- Q₂ : Transfert thermique cédé à l’air de la pièce : Q₂ < 0 J

- Relation :

- ΔU = W + Q₁ + Q₂

3)- Énergie interne d’un système incompressible.

► Système incompressible :

- Un système est incompressible si sa masse volumique ρ est constante.

► Augmentation de la température d’un système incompressible :

- Lorsque l’on augmente la température d’un système incompressible,

- L’énergie cinétique des entités chimiques qui le constitue augmente ;

- Donc son énergie interne U augmente.

► Capacité thermique :

- La capacité thermique C d’un système est égale au produit de la masse m du système par sa capacité thermique massique c.

C = m . c

C : Capacité thermique (J . °C^–1) ou (J . K^–1)

m : masse du système (kilogramme : kg)

C : Capacité thermique massique

(J . kg^–1 . °C^–1) ou (J . kg^–1 . K^–1)

- Quelques capacités thermiques massiques :

Matériau	c (J . kg^–1 . °C^–1) ou (J . kg^–1 . K^–1)
Aluminium Al (s)	897
Eau H₂O (s)	2,06 × 10³
Éthanol C₂H₅OH (ℓ)	2,44 × 10³
Eau H₂O (ℓ)	4,81 × 10³

► Définition de la capacité thermique massique :

- La capacité thermique massique c d’un système incompressible est l’énergie absorbée par

1 kg de ce système pour élever sa température de 1 ° C ou 1 K.

► Transfert par chaleur produisant une élévation de température (sans changement d’état) :

- La variation d’énergie interne ΔU d’une masse m de substance dont la température

varie d’une valeur initiale θ_i à une valeur finale θ_f, sans changement d’état,

est donnée par la relation suivante :

ΔU = m . c . (θ_f – θ_i ) = m . c . Δθ

ΔU : Variation d’énergie interne en joule (J)

m : Masse de la substance en kilogramme (kg)

c : Capacité thermique massique

(J.kg^{– 1}.° C^{– 1}) ou (J.kg^{– 1}. K^{– 1})

θ_f – θ_i = Δθ : Variation de température en (°C) ou (K)

► Remarque 1 :

- On peut travailler avec la température absolu T en kelvin (K)

ΔU = m . c . (T_f – T_i ) = m . c . ΔT

ΔU : Variation d’énergie interne en joule (J)

m : Masse de la substance en en kilogramme (kg)

c : Capacité thermique massique

(J . kg^{–
1}.° C^{– 1}) ou (J.kg^{– 1}.K^{– 1})

T_f –T_i = ΔT : Variation de température absolue en kelvin (K)

► Remarque 2:

- ΔT = Δθ

► Remarque 3 :

- La capacité thermique massique c d’une substance

correspond au transfert thermique nécessaire pour faire

varier de 1 ° C (ou 1 K) une masse de 1 kg de substance.

- Unité : (J.kg^{– 1} .° C^{– 1} ) ou (J . kg^{– 1} . K^{–
1})

► Remarque 4 :

- Si θ_f > θ _i => ΔU = Q > 0, la substance reçoit de l'énergie du milieu extérieur.

- Si θ_f < θ _i => ΔU = Q < 0, la substance cède de l'énergie au milieu extérieur.

► Exemple :

On chauffe de l’eau afin obtenir 80 L d’eau à 80 ° C à partir de 80 L d’eau à 20 ° C.

- Calculer la variation de l’énergie interne du système (les 80 L d’eau à l’état liquide).
- On donne :

- Masse volumique de l’eau : ρ = 1,0 kg / dm³

- Capacité thermique massique de l'eau : c = 4,18 kJ . kg^–1. ° C^–1

- Variation de l’énergie interne du système :

- La température du système augmente.

- La variation de l’énergie interne ΔU du système est positive

- ΔU = Q = m . c . ( θ_f – θ_i )

- ΔU = 80 × 4,18 × (80 – 20)

- ΔU = 2,0 × 10⁴ kJ.

4)- Établir un bilan énergétique .

Un cumulus électrique est une réserve d’eau chauffée par un conducteur ohmique.

En l’absence de chauffage, la température de l’eau chaude qu’il contient diminue au fil des heures.

On souhaite faire le bilan énergétique de l’eau contenue dans le cumulus.

- Définir le système étudié.

- Relever la nature des transferts énergétiques entre le système et le milieu extérieur.

- Repérer le sens des transferts et leur attribuer un signe.

- Présenter le bilan énergétique à l’aide d’un schéma.

► Système étudié : S

- S = {Eau contenue dans le cumulus}

► Nature des transferts énergétiques entre le système et le milieu extérieur.

- La résistance du cumulus, lorsqu’elle est traversée par un courant électrique,

transfère à l’eau de l’énergie électrique par travail électrique W_e.

- La température de l’eau contenue dans le cumulus augmente.

- Lorsque la résistance n’est plus traversée par un courant électrique,

la température de l’eau diminue lentement.

- Le système S cède de l’énergie au milieu extérieur sous forme de transfert thermique Q.

► Sens des transferts et signe :

- L’eau reçoit de l’énergie par travail électrique W_e.

- Cette énergie est comptée positivement : W_e > 0.

- L’eau cède de l’énergie Q par transfert thermique.

- Cette énergie est comptée négativement : Q < 0.

► Schéma du bilan énergétique :

IV- Applications.

1)- Transferts Thermiques. :

Mesure de la capacité thermique massique du laiton.

2)- QCM.

QCM réalisé avec le logiciel Questy

Pour s'auto-évaluer

Premier principe de la thermodynamique et bilan énergétique

Le modèle du gaz parfait et quelques limites

L’énergie interne et les modes de transfert de l’énergie

Le premier principe de la thermodynamique

Sous forme de tableau

3)- Exercices.

Exercices :

1)- Exercice 05 page 312 : Déterminer un volume molaire.

2)- Exercice 07 page 312 : Exprimer une mass volumique.

3)- Exercice 08 page 312 : Calculer une masse volumique.

4)- Exercice 09 page 313 : Définir l’énergie interne.

5)- Exercice 11 page 313 : Connaître l’énergie microscopique.

6)- Exercice 13 page 313 : Distinguer des variations d’énergie.

7)- Exercice 15 page313 : Reconnaître le mode de transfert de l’énergie.

8)- Exercice 17 page 314 : Connaître le premier principe .

9)- Exercice 21 page 314 : Prévoir l’évolution de l’énergie interne.

10)- Exercice 23 page 315 : Pression d’un gaz.

11)- Exercice 26 page 316 : Il y a film et film.

12)- Exercice 29 page 317 : Équation de Van der Waals.

13)- DS N° 01 :Le principe de la montgolfière (30 min) : exercice 31 page 318.

14)- DS N° 02 : Géothermie (50 min) : exercice 32 page 319.

15)- Préparation à ECE : Identification d’un échantillon métallique.