|
Premier principe de la thermodynamique
et bilan énergétique |
|
|
|
|
|
Premier principe de
la thermodynamique
et bilan énergétique
Exercices 24
![]()
I- Exercice 1 : Dissoudre un gaz.
Un ballon de volume
V0
= 250 mL est rempli de chlorure d'hydrogène gazeux
HCℓ (g) à la
pression P0 = 1,013 × 105
Pa.
Le bouchon du ballon est traversé par un tuyau souple
fermé par une pince.
L'extrémité du tuyau est plongée dans un
cristallisoir qui contient de l'eau distillée et quelques gouttes d'hélianthine
qui se colorent en rouge lorsque le pH
est inférieur à 3.
Après l'ouverture de la pince, l'extrémité du tuyau
souple est immergée dans la solution du cristallisoir, la solution aqueuse monte
en jet dans le ballon et se colore en rouge.
Le volume de gaz restant dans le ballon est
V1
= 20 mL à la pression P1 = 9,83 × 104
Pa.


DONNÉES :
En début et en fin d'expérience, la température du
gaz est T =
298 K.
Constante du gaz parfait :
R = 8,314 Pa . m3
.mol–1
. K–1.
QUESTION :
Exprimer puis calculer la quantité de matière de
chlorure d'hydrogène gazeux n
(HCℓ)
initialement introduite dans le ballon.
-
Avant l’expérience du
jet d’eau :
-
Volume du ballon :
V0
= 250 mL
-
Température du gaz :
T = 298 K
-
Gaz : mélange de
chlorure d'hydrogène gazeux HCℓ
(g) et d’air.
-
Pression :
P0 = 1,013 × 105
Pa.
-
En fin d’expérience :
-
Volume de gaz restant
dans le ballon : V1
= 20 mL
-
Pression du g az restant dans le ballon :
P1 = 9,83 × 104
Pa.
-
Le gaz restant dans le
ballon est de l’air.
-
On considère que le
chlorure d’hydrogène gazeux se comporte comme un gaz parfait.
-
De même l’air se
comporte comme un gaz parfait.
-
Dans le cas présent,
la pression des différents gaz est faible.
-
Elle est voisine de la
pression atmosphérique : P0 = 1,013 × 105
Pa et P1 = 9,83 × 104
Pa.
-
Au départ :
-
Quantité de matière de
chlorure d’hydrogène gazeux :
n (HCℓ)
-
Quantité de matière
d’air :
n (air)
-
Quantité de matière de
gaz contenu dans le flacon au départ :
-
ni
=
n (HCℓ)
+ n
(air)
►
Réaction
chimique lors de l’expérience du jet d’eau :
-
Il se produit la
dissolution du chlorure d’hydrogène dans l’eau
-
Cette réaction est
totale.
-
Elle produit une
solution d’acide chlorhydrique :
H3O+
(aq) +
Cℓ–
(aq)
-
Cette solution acide
est mise en évidence par la coloration rouge de l’hélianthine.
-
Équation de la
réaction :
HCℓ
(g) +
H2O
(ℓ) → H3O+
(aq) + Cℓ–
(aq)
-
Tout le chlorure
d’hydrogène a réagi avec l’eau.
-
En fin d’expérience le
gaz restant dans le flacon est l’air de quantité de matière
n
(air)
►
Application de la loi des gaz parfait au mélange initial :
-
Avant l’expérience du
jet d’eau :
-
Volume du ballon :
V0
= 250 mL
-
Température du gaz :
T = 298 K
-
Quantité de matière de
gaz :
ni
=
n (HCℓ)
+ n
(air)
-
mélange de chlorure
d'hydrogène gazeux HCℓ
(g) et d’air.
-
Pression :
P0 = 1,013 × 105
Pa.
-
Loi des gaz parfait :
-
P0 .
V0
= ni
.
R . T
-
![]()
►
Application de
la loi des gaz parfait après l’expérience :
-
Volume du gaz :
V1
= 20 mL
-
Température du gaz :
T = 298 K
-
Quantité de matière de
gaz :
n
(air)
-
Pression :
P1 = 9,83 × 104
Pa
-
P1 .
V1
= n
(air) .
R . T
-
![]()
-
Quantité de matière de
chlorure d’hydrogène gazeux :
n (HCℓ)
-
ni
=
n (HCℓ)
+ n
(air)
-
n (HCℓ)
= ni
– n
(air)
-

-
Application
numérique :
-
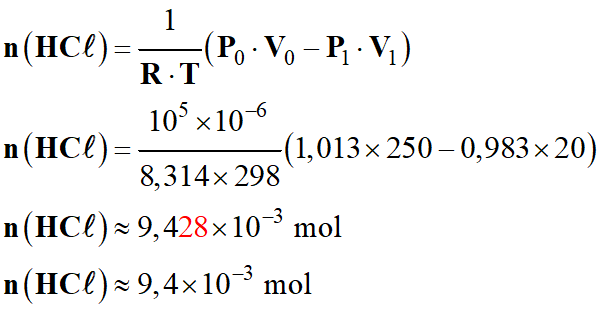
►
Schémas de
l’expérience :
-
Première étape : Sous
la Hotte

-
On porte à ébullition
une solution concentrée d’acide chlorhydrique (37 %).

-
On laisse se
poursuivre l’ébullition pendant 2 min environ.
-
Le chlorure
d’hydrogène est recueilli dans un flacon
-
C’est un gaz plus
dense que l’air.
-
On bouche le flacon
avec un bouchon muni d’un tube fermé par une pince.

-
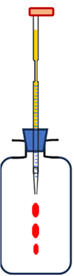
Deuxième étape :
expérience du jet d’eau.
-
On amorce l’aspiration
de l’eau.
-
Pour ce faire, on
retourne le flacon avec son dispositif sur le cristallisoir contenant de l’eau
-
On enlève la pince
pour faire entrer un peu d’eau et on bouche l’extrémité du tube avec l’index
-
On secoue l’ensemble
et le retourne sur le cristallisoir contenant de l’eau.
-
L’eau remplit
partiellement le flacon.
-
L’eau initialement
jaune-orangé se colore en rouge.
- La solution obtenue est acide, son pH est inférieur à 3,1.
Indicateurs colorés acido-basiques
- Schémas : on amorce l'aspiration de l'eau
 On
retourne le dispositif
On
retourne le dispositif

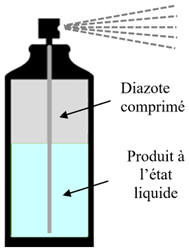
II- Exercice 2 : Stockage des aérosols.
Une bombe aérosol neuve de volume V = 200 mL, contient comme gaz propulseur du diazote, que l'on assimile au gaz parfait.

DONNÉES :
Constante du gaz parfait :
R = 8,314 Pa . m3
.mol–1 . K–1.
1 bar = 105
Pa
Température absolue :
T (K) = θ
° C + 273,15
a)- À la température θ1 = 25,0 °C, le volume V1 du gaz propulseur correspond à 40% du volume du boîtier est à la pression P1= 6,00 bar.
Déterminer la quantité de matière
n1
de gaz propulseur présent dans ce dispositif.
b)- Déterminer la température θ2 pour atteindre la pression maximale P2 = 10,0 bar que peut supporter la bombe aérosol neuve en toute sécurité,
en supposant que le volume
V2
et la quantité de matière
n2
du gaz propulseur restent constants.
c)-
Indiquer si cette situation peut se
produire dans la vie courante.
d)- Au cours de l'utilisation du produit, la pression du gaz propulseur diminue.
À la température θ1 = 25,0 °C, quand sa pression atteint la valeur P3 = 3,00 bar, le gaz propulseur occupe un volume V3 = 160 mL
et le dispositif ne fonctionne plus.
En déduire un inconvénient du conditionnement aérosol, d'un déodorant par
exemple.
Le contenu d’un aérosol au gaz
diazote propulseur :
Un aérosol est un récipient sous pression qui
utilise du gaz pour expulser le liquide qu’il contient.
Le diazote est produit à partir d’air comprimé.
Des machines séparent les molécules de dioxygène et
de diazote gazeux.
On utilise principalement le diazote dans les eaux
thermales.
C’est l’un des seuls gaz acceptés par Ecocert
pour les produits cosmétiques.
Les aérosols offrent une grande commodité et efficacité, mais ils présentent également des défis en termes de santé et d’environnement.
a)-
Quantité de matière
n1 de gaz propulseur
présent dans ce dispositif.
-
Température θ1 = 25,0
°C
-
La température absolue du gaz, notée T
-
Température absolue : T (K) = θ ° C + 273,15
-
Température T1 = 25,0
°C + 273,15
-
T1
≈ 298 °C
-
Volume
V1 du gaz propulseur
correspond à 40% du volume du boîtier
-
Bombe
aérosol neuve de volume V = 200
mL
-
Pression
P1 = 6,00 bar
-
Quantité
de matière de gaz propulseur : n1 ?
-
On considère que le diazote se comporte comme un
gaz parfait.
-
Loi des gaz
parfait :
-
P1 .
V1 = n1
. R . T
-
![]()
-
Avec V1
= 0,400
V
-
Application
numérique :
-
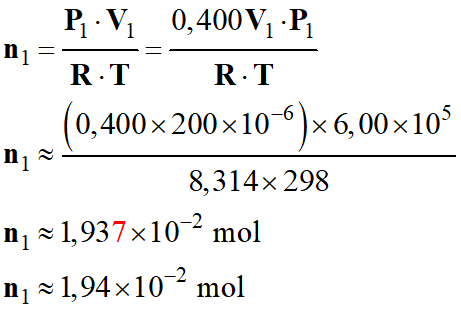
b)-
Température
θ2 pour atteindre la
pression maximale P2 =
10,0 bar que peut supporter la bombe aérosol neuve.
-
Volume
V2 =
V1
-
Quantité
de matière n2 du gaz propulseur :
n2 = n1
-
Température : T2 = 273 + θ2
-
Pression
maximale : P2 = 10,0 bar
-
Loi des gaz
parfait :
-
P2 .
V2 = n2
. R . T2
-
Application
numérique :
-
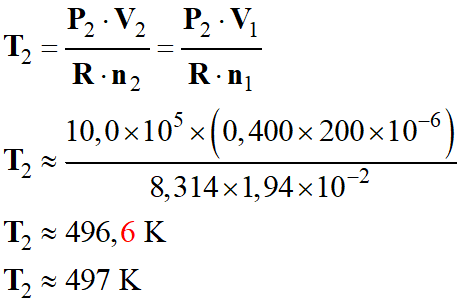
-
T2
≈ 273 + θ2
-
θ2
≈ T2 – 273
-
θ2
≈
497 – 273
-
θ2
≈ 224 ° C
c)-
Indiquer si cette situation peut se
produire dans la vie courante.
-
Cette situation peut se produire lors d’un
incendie ou si l’on place l’aérosol près d’une flamme ou dans un four.
-
Dans les
conditions quotidiennes, on ne peut pas atteindre de telles températures.
d)-
Inconvénient du
conditionnement aérosol, d'un déodorant par exemple.
-
Au cours de l'utilisation du produit, la pression
du gaz propulseur diminue.
-
À la
température θ1 = 25,0 °C,
-
Quand sa
pression atteint la valeur P3 = 3,00, bar,
-
le gaz
propulseur occupe un volume V3 = 160 mL
-
le dispositif ne
fonctionne plus.
-
Quantité de
matière de gaz propulseur restant dans le flacon :
-
Loi des gaz
parfait :
-
P3 .
V3 = n3
. R . T1
-
![]()
-
Application
numérique :
-

-
La quantité de
matière de gaz propulseur n’a pratiquement pas variée.
-
Le flacon aérosol
n’est pas vide. Il reste aussi du produit non utilisé à l’intérieur du
flacon.
-
Ce flacon présente
toujours un danger d’explosion lors d’un indencie, lors d’une surchauffe.
-
Il faut recycler
ce type de flacon.
-
Suivre les
instructions écrites sur le flacon.
-
Les bombes aérosol
qui ne sont pas vides doivent être jetées différemment, car il peut être
dangereux de les jeter de façon classique.
-
Les bombes aérosol
sont pressurisées, ce qui signifie qu'elles sont susceptibles d'exploser si
elles sont modelées.
-
N'essayez jamais
de perforer une bombe aérosol, ni de l'exposer à une chaleur extrême.
-
Si le contenant
est équipé d'un bouchon en plastique, vous pouvez le retirer pour le
recycler.
III- Exercice 3 : Prévoir la variation d’une grandeur.
Un élève cherche à appliquer comment augmenter la
masse volumique d'un gaz en faisant varier les grandeurs macroscopiques qui
le décrivent.
ÉTAPE 1 :
Comprendre ce que l'on peut déduire de l'équation d'état du gaz parfait.
Un petit quiz pour commencer …
|
Si P
augmente alors T augmente :
Si V
augmente alors n augmente :
Si P
augmente alors n augmente :
Si P ×
V augmente alors T augmente :
|
|
|
…étonnant non.
►
Dans
chaque cas l'affirmation est toujours vraie à condition que le reste des
variables soient constantes.
►
On peut donc dire sur le
premier exemple :
►
« si P
augmente alors T
augmente est toujours vrai si n
et V
restent constantes ».
►
La seule certitude est
que le rapport
![]() ( R
constante des gaz parfaits) est constant quelles que soient les valeurs de
n,
V,
P et
T !
( R
constante des gaz parfaits) est constant quelles que soient les valeurs de
n,
V,
P et
T !
ÉTAPE 2 :
Isolé la grandeur physique souhaitée.
Le support visuel ci-dessous présente les étapes et
les résultats d'une démarche mise en œuvre pour isoler une variable de
l'équation d'état du gaz parfait.

Par exemple, exprimer V en fonction de P,
T, R et n pour une pression non nulle (P ≠ 0) :
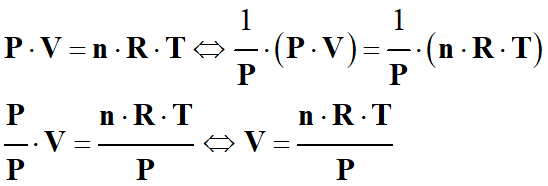
►
Conseils ! Pour analyser les
données du problème.
►
Lorsqu’une grandeur
physique est recherchée dans un problème, les autres grandeurs dont elle
dépend sont déterminées soit directement à partir des données, soit
indirectement à l'aide d'expressions connues.
►
Exemple, si la température T est
demandée, il faut pouvoir extraire P, V et
n des données ou, si besoin ,utiliser des relations connues
faisant intervenir ces grandeurs comme :
-
Relation reliant
quantité de matière n,
à la masse
m et à la masse molaire M :
-
![]()
-
Relation reliant, la masse
m, la
masse volumique ρ et le volume
V:
-
m
= ρ .
V
- etc…
Questions :
1.
Exprimer la masse volumique ρ
d’un gaz, de masse m, contenu dans une enceinte fermée de volume V
variable et dont la température T est susceptible d'être modifiée.
2.
Écrire l’équation d’état du gaz
parfait et y faire intervenir la masse volumique ρ.
3.
Isoler la masse volumique ρ.
4.
En déduire les différentes
façons d'augmenter la masse volumique d'un gaz, en précisant pour chacune
d’elles, les paramètres qui restent constants.
1.
Expression de la masse volumique ρ d’un
gaz :
-
Masse du gaz :
m
-
Volume du gaz :
V variable
-
Température du gaz
T (susceptible d'être
modifiée)
-
Relation reliant, la masse
m, la
masse volumique ρ et le volume
V:
-
m
= ρ .
V
-
Autre écriture :
-
![]()
-
Relation reliant
quantité de matière n,
à la masse
m et à la masse molaire M :
-
![]()
-
On peut écrire
l’expression suivante :
-
![]()
2.
Équation d’état du gaz parfait.
-
Expression en
fonction de la masse volumique
ρ
-
Pour faire
intervenir la température T, on
utilise l’équation d’état du gaz parfait :
-

3.
Isoler la masse volumique
ρ.
-
Expression de la
masse volumique ρ à partir de
l’équation d’état du gaz parfait :
-
![]()
4.
Les différentes façons d'augmenter la
masse volumique d'un gaz :
-
La masse volumique
ρ augmente si le rapport
![]() augmente.
augmente.
-
Or
R est la constante des gaz
parfaits et M représente la masse
molaire du gaz.
-
La masse molaire
M d’un gaz est une grandeur caractéristique du gaz, elle ne varie
pas.
-
La masse volumique
ρ d’un gaz augmente :
-
Si la pression
P du gaz augmente à température
T constante.
-
Si la température
T du gaz diminue à pression constante
P
-
Si la pression
P et la température T
varient de telle sorte que le rapport
![]() augmente.
augmente.
IV- Exercice 4 : Suivi cinétique d'une transformation chimique.
Les pluies acides sont des précipitations qui peuvent
contenir de l'acide sulfurique résultant de la combustion des combustibles
fossiles.
Cet acide est susceptible de réagir avec le zinc
présent dans les gouttières.
Pour étudier la transformation chimique entre l'acide
sulfurique et le zinc, considéré comme totale, on réalise l'expérience
décrite dans le DOC. 1.
L'étude a comme objectif de retrouver expérimentalement
la valeur de l'avancement maximal xmax de la réaction
attendue théoriquement.
DOC. 1 Description de l’expérience

À la date t = 0 s, on verse rapidement, sur une
masse m = 0,50 g de poudre de zinc, un volume V = 75,0 mL de
solution d’acide sulfurique de concentration en ions oxonium H3O+
(aq), C = 0,40 mol . L–1.
La pression est mesurée à cet instant par le capteur
est P0 = 1020 hPa.
La formation de dihydrogène crée une surpression qui
s’additionne à la pression de l’air initialement présent.
DOC. 2 Tableau de valeurs.
|
t
( en min) |
0 |
1,0 |
3,0 |
5,0 |
7,0 |
9,0 |
11,0 |
15,0 |
20,0 |
25,0 |
30,0 |
35,0 |
|
P
(en hPa) |
1020 |
1030 |
1060 |
1082 |
1101 |
1120 |
1138 |
1172 |
1215 |
1259 |
1296 |
1335 |
|
t
( en min) |
45,0 |
50,0 |
60,0 |
70,0 |
80,0 |
90,0 |
110,0 |
140,0 |
160,0 |
190,0 |
240,0 |
300,0 |
|
P
(en hPa) |
1413 |
1452 |
1513 |
1565 |
1608 |
1641 |
1697 |
1744 |
1749 |
1757 |
1757 |
1757 |
DONNÉES :
Masse molaire atomique du zinc : M (Zn) =
65,4 g . mol–1
Constante du gaz parfait : R = 8,314 Pa . m3
.mol–1 . K–1.
1 bar = 105 Pa
Température absolue : T (K) = θ ° C +
273,15
L’équation de la réaction modélisant la transformation
du zinc en milieu acide :
Zn (s) + 2 H3O+
(aq) → Zn2+ (aq) + H2 (g) + H2O
(ℓ)
Questions :
1.
À partir du DOC. 1, établir un tableau d’avancement de la réaction et déterminer l’avancement maximal xmax.2. En considérant que le dihydrogène libéré par la réaction est un gaz parfait et en négligeant le volume de solution d’acide sulfurique versé devant le volume d’air initialement présent dans l’erlenmeyer, montrer que l’avancement x de la réaction a pour expression :
 où
l’on note Pmax la pression mesurée à
l’état final.
où
l’on note Pmax la pression mesurée à
l’état final.3.
Tracer la courbe d’évolution de l’avancement x de la réaction en fonction du temps avec un tableur.4.
Vérifier que l’avancement maximal xmax obtenu en 1. est en accord avec l’avancement xf déterminé graphiquement, en justifiant les écarts éventuels.
1.
Tableau d’avancement de la réaction et avancement
maximal xmax.
-
Quantité de matière initiale d’ions oxonium :
-
n
(H3O+) =
C .
V
-
n
(H3O+) = 0,40 × 75 × 10–3
-
n
(H3O+) ≈ 3,0 × 10–2 mol
-
n
(H3O+) ≈ 30 mmol
-
Quantité de matière initiale de zinc :
-

-
Tableau d’avancement :
|
Équation de la réaction |
|||||||
|
Équation |
|
2
H3O+
(aq) |
+
Zn (s)
|
→ |
Zn2+
(aq) |
+ H2
(g) |
+ 2
H2O (ℓ) |
|
État du
système |
Avanc. |
n (H3O+) |
n (Zn) |
|
n (Ca2+) |
n (H2) |
solvant |
|
État initial
(mmol) |
x =
0 |
n0 (H3O+) ≈ 30 |
n0 (Zn) ≈ 7,6 |
|
0 |
0 |
solvant |
|
Au cours
de la
trans. |
x |
n0 (H3O+) – 2 x |
n0 (Zn) – x |
|
x |
x |
solvant |
|
Avanc.
maximal |
xmax |
n0 (H3O+) – 2 xmax1
= 0 |
n0 (Zn) – xmax2
= 0 |
|
xmax |
xmax |
solvant |
-
Recherche de l’avancement maximal :
-
Hypothèse 1 : On suppose que l’ion oxonium
est le réactif limitant :
-
Dans ce cas :
-
n0
(H3O+)
– 2 xmax1 = 0
-
30 – 2 xmax1 ≈ 0
-
xmax1
≈15 mmol
-
Hypothèse 2 : on suppose que le zinc est le
réactif limitant :
-
n0
(Zn) –
xmax2 = 0
-
7,6 –
xmax2 ≈ 0
-
xmax2
≈ 7,6 mmol
-
Or l’avancement maximal est égal à la plus
petite des deux valeurs :
-
xmax
= xmax2 <
xmax1
-
xmax
≈ 7,6 mmol
-
Le zinc est le réactif limitant et l’ion
oxonium est le réactif en excès :
-
Tableau d’avancement et bilan de matière :
|
Équation de la réaction |
|||||||
|
Équation |
|
2
H3O+
(aq) |
+
Zn (s)
|
→ |
Zn2+
(aq) |
+ H2
(g) |
+ 2
H2O
(ℓ) |
|
État du
système |
Avanc. |
n (H3O+) |
n (Zn) |
|
n (Ca2+) |
n (H2) |
solvant |
|
État initial
(mmol) |
x =
0 |
n0
(H3O+) ≈ 30 |
n0
(Zn) ≈ 7,6 |
|
0 |
0 |
solvant |
|
Au cours
de la
trans. |
x |
n0
(H3O+) – 2 x |
n0
(Zn) – x |
|
x |
x |
solvant |
|
Avanc.
Maximal
(mmol) |
xmax |
n0
(H3O+) – 2 xmax
14,7 ≈ 15 |
n0
(Zn) – xmax
= 0 |
|
xmax
7,6 |
xmax
7,6 |
solvant |
2.
Expression de l’avancement x de la réaction.
-
À la lecture du tableau d’avancement de la
réaction, on peut écrire l’égalité suivante :
-
n (H2)
= x
-
D’après l’énoncé :
-
La pression est mesurée, à
t0 = 0 s par le capteur est, P0 = 1020
hPa.
-
La formation de dihydrogène crée une
surpression qui s’additionne à la pression de l’air initialement présent :
-
P
(H2) =
P – P0
-
On note le volume du gaz :
Vgaz
-
On considère que le dihydrogène se comporte
comme un gaz parfait.
-
On peut utiliser l’équation des gaz
parfaits :
-
P
(H2) .
Vgaz = n (H2)
. R .
T
-
Expression de l’avancement :
-

-
Dans l’expression, il faut faire intervenir
l’avancement maximal xmax et la pression maximale Pmax.
-
Or l’avancement est maximal xmax
lorsque la pression est maximale Pmax :
-
![]()
-
En conséquence :
-
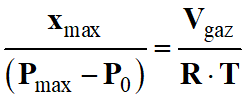
-
En combinant les relations :
![]() et
et 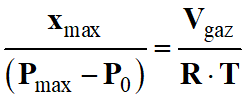
-
On peut donner l’expression de l’avancement
x de la réaction:
-

3.
Courbe d’évolution de l’avancement x de la
réaction en fonction du temps avec un tableur.
-
Utilisation du tableur Excel :

-
Formule pour le calcul :
Cellule E4
-
Formule que l’on recopie vers le bas autant
que nécessaire.
-
Tableau de valeurs :
|
t
(en min) |
P
(en hPa) |
x
mmol |
|
0 |
1020 |
0,00 |
|
1 |
1030 |
0,10 |
|
3 |
1060 |
0,41 |
|
5 |
1082 |
0,64 |
|
7 |
1101 |
0,84 |
|
9 |
1120 |
1,03 |
|
11 |
1138 |
1,22 |
|
15 |
1172 |
1,57 |
|
20 |
1215 |
2,01 |
|
25 |
1259 |
2,46 |
|
30 |
1296 |
2,85 |
|
35 |
1335 |
3,25 |
|
45 |
1413 |
4,05 |
|
50 |
1452 |
4,45 |
|
60 |
1513 |
5,08 |
|
70 |
1565 |
5,62 |
|
80 |
1608 |
6,06 |
|
90 |
1641 |
6,40 |
|
110 |
1697 |
6,98 |
|
140 |
1744 |
7,47 |
|
160 |
1749 |
7,52 |
|
190 |
1757 |
7,60 |
|
240 |
1757 |
7,60 |
|
300 |
1757 |
7,60 |
-
Graphe : x = f (t) :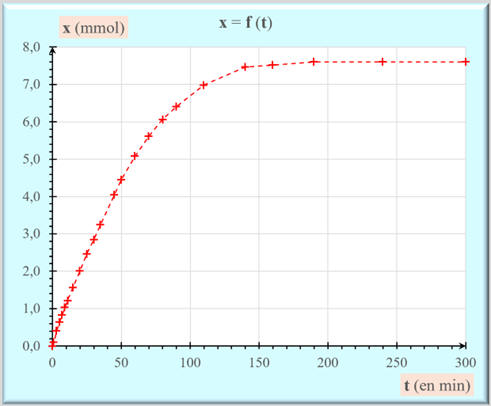
-
L’avancement
x varie rapidement au départ de la réaction, puis plus lentement.
-
C’est le régime transitoire.
-
En fin de réaction, lorsque la réaction est
terminée, l’avancement x ne varie
plus.
-
C’est le régime permanent.
-
On peut déterminer de façon graphique la
valeur de l’avancement final xf
de la réaction :
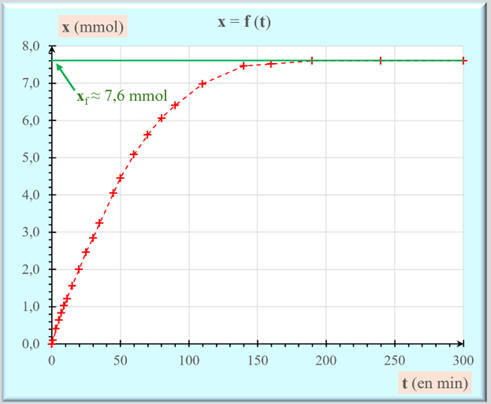
-
xf
≈ 7,6 mmol
-
On peut déterminer aussi le temps de
demi-réaction :
-
Définition du temps de demi-réaction
-
Le temps de demi-réaction
t1/2 correspond à la durée au bout de laquelle
l’avancement atteint la moitié de sa valeur finale
xf :
-
![]()
-
Exploitation du graphique :

-
t1/2
≈ 42 min
-
La réaction est terminée au bout de 6 t1/2
environ.
4.
Comparaison de l’avancement maximal xmax
obtenu en 1. et de l’avancement xf déterminé
graphiquement.
-
La transformation chimique entre l'acide
sulfurique et le zinc, considéré comme totale :
Zn (s) + 2 H3O+
(aq) → Zn2+ (aq) + H2 (g) + H2O
(ℓ)
-
En conséquence :
xf = xmax
-
Le zinc est le réactif limitant. En fin de
réaction il est totalement consommé.
-
xf
= xmax ≈ 7,6 mmol
-
L’exploitation graphique est en accord avec
l’avancement maximal calculé à la question 1.
-
justification des écarts éventuels :
-
Il faut faire en sorte que le dispositif soit
bien étanche : pas de fuite de gaz.
-
La température
T du milieu réactionnel doit rester constante au cours de la
réaction.
-
Pour ce faire, on utilise un bain
thermostaté.
-
La variation de volume lorsque l’on verse la
solution d’acide sulfurique doit être négligeable devant le volume de
l’erlenmeyer.
-
Ne pas oublier que l’on utilisé l’équation
d’état des gaz parfaits : P .
V =
n . R .
T
-
Si V
et T sont constant au cours de
l’expérience, alors la variation de P
est liée à la variation de n.
-
V- Exercice 5 : Des bouchons sous pression.
Le champagne doit son effervescence au dioxyde de
carbone dissous (CO 2) qui est libéré sous forme de gaz à
l'ouverture du bouchon.
Il contient entre 5 et 9 g dans une bouteille.
DOC. 1 Dissolution du dioxyde de carbone dans l’eau
La concentration C de gaz dissous dans une
solution aqueuse est proportionnelle à la pression P qu'exerce ce gaz
sur le liquide d'après la loi de Henri (1803).
Cela se traduit par la relation C = kT
× P, avec kT
la constante de Henri qui est fonction de la température T du composé
chimique étudié.
À T = 298 K, la constante de Henri vaut pour
le dioxyde de carbone :
kT = 3,35 × 10–7
mol . L–1 . Pa–1

DOC. 2 Chronophotographie du bouchon initialement
immobile
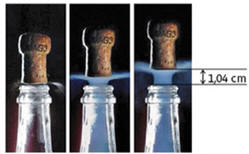
Intervalle temporel τ entre deux clichés :
τ = t1
–
t0
= t2
–
t1
= 400 μs
La force
pressante, modélisant l'action exercée par le gaz contenu dans la bouteille
sur le bouchon, est constante pendant 2 ms après la libération du bouchon.
Il règne
une pression dans la bouteille telle que le bouchon éjecté verticalement, à
température ambiante, pourrait atteindre une hauteur comprise entre 8 m et 9
m en l'absence de frottement de l'air.
DOC. 3
Caractéristiques de la bouteille de
champagne.

DONNÉES :
-
Tambiante
= 298 K
-
Patmosphérique
= 1013 hPa
-
Intensité de la pesanteur :
g = 9,81 N . kg–1
-
Constante des gaz parfaits : R = 8,314 Pa . m3 .mol–1
. K–1.
-
Dans le référentiel galiléen, la variation
approchée entre le vecteur variation de vitesse
![]() d’un système modélisé par un point de
masse m et la somme
d’un système modélisé par un point de
masse m et la somme
![]() des
vecteurs forces appliquées à ce système
pendant une durée Δt séparant
deux instants voisins est la suivante :
des
vecteurs forces appliquées à ce système
pendant une durée Δt séparant
deux instants voisins est la suivante :
- ![]()
-
Les unités SI :
- ![]() en m . s–1 ; m
en kg ;
en m . s–1 ; m
en kg ;
![]() en N ;
Δt en s
en N ;
Δt en s
Question :
► Estimer la quantité de matière de dioxyde de carbone contenu dans une bouteille de champagne
en portant un regard
critique sur le résultat obtenu au regard des hypothèses formulées.
-
On veut estimer la quantité de matière de
dioxyde de carbone contenu dans une bouteille de champagne.
►
Cheminement du raisonnement :
-
On connait le volume de
CO2 (g), Vg
= 6,50 cm3
-
Pour connaître la pression du gaz, on
considère que le dioxyde de carbone se comporte comme un gaz parfait.
-
Équation état des gaz parfaits :
Pg .
Vg = n .
R .
T
-
D’autre part :
-
On donne dans l’énoncé, le diamètre intérieur
du goulot : d = 2,08 cm
-
Ainsi, on peut accéder à la force pressante
exercée par le gaz sur le bouchon :
-
Fg
= Pg .
S
-
Pour atteindre la force pressante
![]() , il faut
réaliser une étude dynamique du mouvement du bouchon et utiliser la deuxième
loi de Newton.
, il faut
réaliser une étude dynamique du mouvement du bouchon et utiliser la deuxième
loi de Newton.
-
En conclusion :
-
Dans un premier temps, on va réaliser une
étude dynamique du système bouchon.
-
Puis dans un deuxième temps, on utilise
l’équation d’état des gaz parfaits (on considère que le dioxyde de carbone
se comporte comme un gaz parfait).
►
Étude dynamique :
-
Comme référentiel, on peut choisir la
bouteille qui est liée à la Terre :
-
Référentiel terrestre supposé galiléen :
-
![]()

-
Bilan des forces :
-
On se place à l’instant
t = 0 s, juste après l’ouverture du bouchon :

-
Le poids du bouchon : ![]()
-
Force verticale, orienté du haut vers le
bas : ![]()
-
Force pressante exercée par l’air extérieur :
-
![]() force verticale, orientée du haut vers le
bas :
force verticale, orientée du haut vers le
bas :
-
![]()
-
Force pressante exercée par le dioxyde de
carbone situé à l’intérieur de la bouteille :
-
![]() force verticale, orientée du bas vers le
haut:
force verticale, orientée du bas vers le
haut:
-
![]()
-
Schéma :
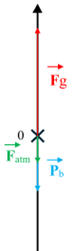
-
On considère que la force pressante
![]() est
constante pendant 2 ms lors de l’éjection du bouchon.
est
constante pendant 2 ms lors de l’éjection du bouchon.
-
Le bouchon est animé d’un mouvement
rectiligne vertical orienté du bas vers le haut.
►
Deuxième loi de Newton :
Relation approchée (classe de
première) :
|
- Dans un référentiel donné, si un système de masse m constante est soumis à une ou plusieurs forces constantes,
le vecteur variation
de vitesse et la somme de
ces vecteurs forces
|
|
|
Valeur de la
force F en newton (N) |
|
Valeur de la
masse m en kilogramme (kg) |
|
|
Valeur de la
durée Δt en seconde (s) |
Énoncé final .
|
-
Dans un référentiel galiléen, la somme
des vecteurs forces de masse m et de centre de masse G,
est égal au produit de sa masse m
par le vecteur accélération
|
|
|
Valeur des
forces F en newton (N) |
|
Valeur de la
masse m en kilogramme (kg) |
|
|
Valeur de l’accélération aG en mètre par seconde au carré (m
. s–2) |
-
Dans le cas présent :
-
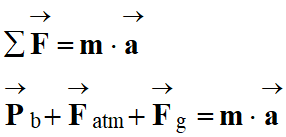
-
Pour pouvoir continuer, on utilise la
chronophotographie du mouvement du bouchon :
-
Chronophotographie du bouchon initialement
immobile

Intervalle temporel τ entre deux clichés :
τ = t1
–
t0
= t2
–
t1
= 400 μs
-
Et la relation approchée : ![]()
-
Relation que l’on peut écrire sous une autre
forme :
-
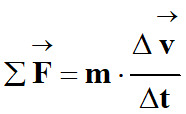
-
Le vecteur
![]() représente le vecteur variation du
vecteur vitesse.
représente le vecteur variation du
vecteur vitesse.
-
En prenant deux instants très proches comme
t0 et
t1 :
-
t1 –
t0 =
τ = 400 μs
-
![]()
-
Par analogie avec le vecteur vitesse, on peut
déterminer l’expression du vecteur accélération au temps
t1 :
-

-
Comme au temps
t = t0, le
bouchon est immobile , v0
= 0 m / s :
-

-
Détermination de la valeur de
v1 :
-
On utilise le fait que la vitesse au temps
t1 est pratiquement
égale à la vitesse moyenne calculée pendant un intervalle de temps très
court encadrent l’instant considéré :
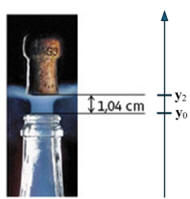
-
![]()
-
On peut utiliser l’expression approché pour
la deuxième loi de Newton car τ est un intervalle de temps très court :
-
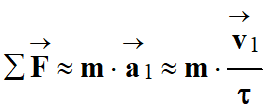
-
En projetant cette relation sur l’axe
y’Oy :
-
![]()
-
Les différentes expressions en fonction de la
pression :
-
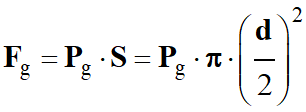
-
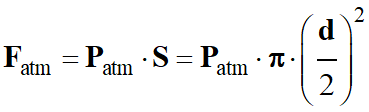
-
On tire l’expression suivante :
-

-
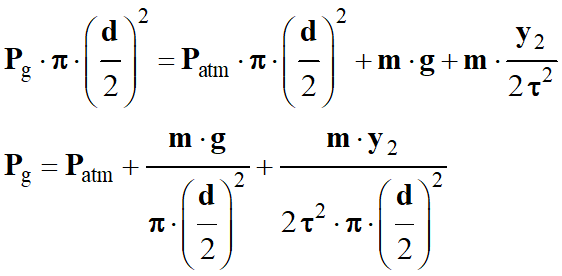
► Quantité de matière, équation d'état des gaz parfaits
et loi de Henry- Quantité de matière de
CO2 :
-
Le dioxyde de carbone est présent sous forme
gazeuse, ng dans le
petit volume situé au-dessus du champagne mais, il est aussi présent
dissous, nd dans le volume
V0 de champagne.
-
n
(CO2) =
ng + nd
-
À partir de l’équation d’état des gaz
parfaits, on peut exprimer la
quantité de matière ng
-
Pg
× Vg = ng
× R ×
T
-
![]()
-
À partir de la loi de Henry, on peut exprimer
la concentration C = kT × P
de dioxyde de carbone et la
quantité de matière correspondante nd.
-
Cd = kT × Pg
-
nd
= Cd ×
V0
-
nd
= kT × Pg × V0
-
Expression de
n (CO2)
-
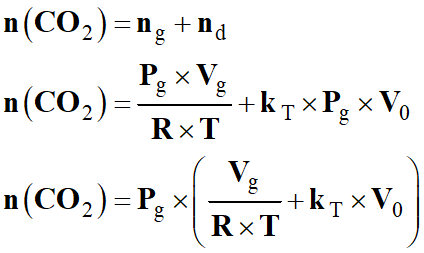
-
Or :
-

-
On peut calculer la valeur de
Pg :
-
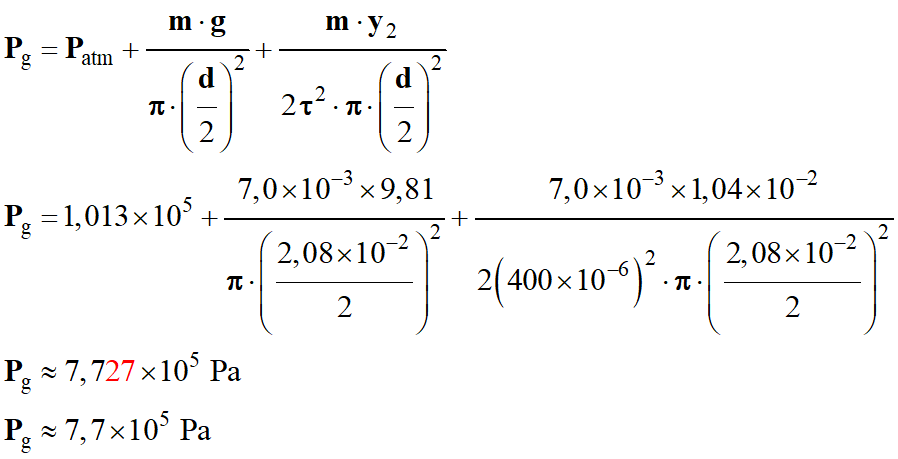
-
Application numérique :
-

-
Masse de
CO2 correspondante :
-
m
(CO2) =
n (CO2) .
M (CO2)
-
m
(CO2) ≈ 0,20 × 44
-
m
(CO2) ≈ 8,63
g
-
m
(CO2) ≈ 8,6 g
-
Malgré les approximations et les
modélisations, le résultat est compatible avec l’indication :
-
« Le champagne doit son effervescence au
dioxyde de carbone dissous (CO2) qui est libéré sous
forme de gaz à l'ouverture du bouchon.
Il contient entre 5 et 9 g dans une bouteille ».
-
Effervescence du champagne :
-
La loi de Henry stipule que la concentration
d’un gaz dissous dans un liquide est proportionnelle à la pression partielle
de ce gaz au-dessus du liquide.
-
Pour le
CO2 dans le champagne,
cela signifie que plus la pression du
CO2 est élevée dans la bouteille, plus la concentration
de CO2 dissous dans le
champagne sera élevée.
-
Lorsqu’on ouvre la bouteille, la pression
diminue brusquement, ce qui entraîne la formation de bulles de
CO2.
-
À l’ouverture de la bouteille, la pression
partielle de CO2
diminue, ce qui réduit la solubilité du
CO2 dans le liquide.
-
Le CO2
dissous excédentaire forme alors des bulles, créant l’effervescence
caractéristique du champagne.
- On remarque que la pression du CO2 dans la bouteille de champagne est environ 7 fois supérieure à la pression atmosphérique.
- Les
bouteilles de champagne sont plus épaisses que les autres bouteilles.
Bouteille de
champagne — Wikipédia (wikipedia.org)
VI- Exercice 6 : Bilan énergétique.
Une pompe à chaleur (PAC) est une machine cyclique
qui peut être utilisée pour chauffer une piscine.
Au terme d'un cycle, le fluide frigorigène de la
PAC
se retrouve dans le même état qu'initialement :
La variation d'énergie interne ΔU du système
{Fluide} est nulle.
Des transferts énergétiques QF,
QC et We sont mise en jeu au cours du
cycle, comme indiqué sur le schéma ci-dessous (We,
l’énergie électrique consommée par la PAC, est transférée intégralement au
fluide de la PAC sous une autre forme d’énergie).
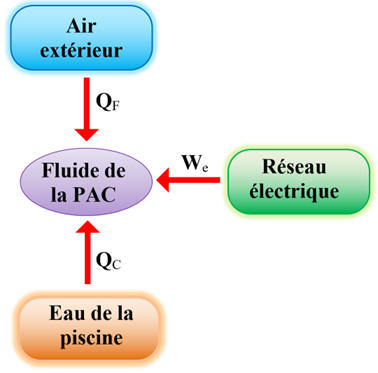
Une PAC chauffe l'eau d'une piscine de volume V
= 60 m3 à une température initiale θi =
17,0 °C.
Au cours d'un cycle, le fluide reçoit de l'énergie
au contact de l'air extérieur et transfère cette énergie à l'eau de la
piscine.
La température de l'eau de la piscine augmente
jusqu'à θf = 28 °C.
Le transfert thermique de la PAC sert intégralement
à chauffer l'eau du bassin.
Dans ces conditions, We = 8,00 ×
109 J
Données :
-
Capacité thermique massique de l'eau liquide : ceau = 4,18 kJ . kg–1 . K–1.
-
Masse volumique de l'eau liquide dans les conditions de l'étude :
-
ρeau = 1000 . kg . m–3
a)-
Déterminer le signe des grandeurs
QF,
QC et
We.
b)-
Réaliser un bilan énergétique sur le système {Fluide} pour un
nombre entier de cycles. En déduire que
QF =
–
QC –
We.
c)-
Calculer la variation d’énergie interne ΔUeau de
l’eau du bassin lors du chauffage de Ti à Tf
et en déduire la valeur de QC, puis de QF.
a)-
Signe des
grandeurs QF,
QC
et We.
►
Travail et transfert thermique :
-
Le travail
W et le
transfert thermique Q
sont des grandeurs algébriques.
-
Par convention :
-
Le travail
W et le
transfert thermique Q
sont comptés positivement
s’ils sont reçus par le système.
-
Le travail
W et le
transfert thermique Q
sont comptés
négativement s’ils sont cédés par le
système.
-
Le bilan
énergétique dépend du système choisi.
-
Avant tout bilan,
il faut préciser le système d’étude.
-
L’énergie d’un
système varie s’il reçoit ou cède de l’énergie.
-
Schéma des
transferts énergétiques :

-
Le
système étudié est le fluide de la
PAC :
système {Fluide}
-
Le
système reçoit le travail électrique
We
du réseau électrique :
We
> 0
-
Le
système reçoit le transfert thermique
QF,
de l’air du milieu extérieur :
QF
> 0
-
Le système chauffe
l’eau de la piscine.
-
Le
système cède le transfert thermique
QC
à l’eau de la piscine :
QC
< 0
b)-
Bilan énergétique du
système {Fluide} pour un nombre entier de cycles.
-
Au terme d'un
cycle, le fluide frigorigène de la PAC se retrouve dans le même état
qu'initialement :
-
La variation
d'énergie interne ΔU
du système {Fluide} est nulle : ΔU
= 0
►
Premier
principe de la thermodynamique :
-
La variation
ΔUi→f
d’énergie interne d’un système,
-
Qui n’échange pas
de matière avec le milieu extérieur,
-
Au repos
macroscopique,
-
Qui évolue d’un
état initial (i) à un état final (f)
-
Est égale à la
somme des énergies échangées par le système avec le milieu extérieur,
-
Par travail
W et / ou par
transfert thermique Q :
|
ΔUi→f
= W + Q |
|
ΔUi→f
: Variation d’énergie interne (joule : J) |
|
W :
Travail (électrique ou mécanique) (joule :
J) |
|
Q :
Transfert thermique (joule : J) |
-
Remarques :
-
L’énergie
mécanique d’un système au repos macroscopique dans le référentiel d’étude
est constante.
-
Le premier
principe de la thermodynamique relie la variation d’énergie interne aux
transferts d’énergie.
-
Il permet
d’établir le bilan énergétique d’un système qui n’échange pas de matière
avec le milieu extérieur.
-
Dans le cas
présent :
-
ΔU
=
QF
+ QC
+ We
= 0
-
En conséquence :
-
QF
= –
QC
–
We
c)-
Variation
d’énergie interne ΔUeau
de
l’eau du bassin lors du chauffage de Ti
à Tf.
-
L’eau est un
système incompressible :
►
Énergie
interne d’un système incompressible.
-
Système
incompressible :
-
Un système est
incompressible si sa masse volumique ρ
est constante.
-
Augmentation de la
température d’un système incompressible :
-
Lorsque l’on
augmente la température d’un système incompressible,
-
L’énergie
cinétique des entités chimiques qui le constitue augmente ;
-
Donc son énergie
interne U
augmente.
►
Transfert par chaleur produisant une élévation de température (sans
changement d’état) :
-
La variation
d’énergie interne ΔU
d’une masse m
de substance dont la température varie d’une valeur initiale
θi
à une valeur finale θf,
sans changement d’état, est donnée par la relation suivante :
|
ΔU
= m . c . (θf
– θi ) = m . c . Δθ
|
|
ΔU :
Variation d’énergie interne en joule (J) |
|
m :
Masse de la substance en kilogramme (kg) |
|
c :
Capacité thermique massique
(J.kg – 1.°
C– 1) ou (J.kg – 1. K– 1) |
|
θf
– θi =
Δθ
: Variation de température
en (°C) ou (K) |
-
Dans le cas
présent avec les notations de l’énoncé :
-
ΔUeau = meau
. ceau
. (θf
– θi
)
-
ΔUeau = ρeau
. V . ceau
. (θf
– θi
)
-
Application
numérique :
-
ΔUeau =
1000
× 560 × 4,18 × 103
× (28 – 17 )
-
ΔUeau ≈
2,57
× 1010
J
-
ΔUeau ≈
2,6
× 1010
J
-
Dans ces
conditions, We
= 8,00 × 109 J
-
Et de plus :
-
QF
= –
QC
–
We
-
Or, le transfert
thermique de la PAC sert intégralement à chauffer l'eau du bassin
-
L’énergie reçue
par l’eau correspond à l’énergie cédée par le système {fluide} :
-
QC
=
–
ΔUeau
-
Valeur de
QC :
-
QC
≈
– 2,6
× 1010
J
-
Valeur de
QF :
-
QF
= –
QC
–
We
-
QF
≈
2,6
× 1010
– 8,00 × 109
J
-
QF
≈ 1,77
× 1010 J
-
QF
≈ 1,8 × 1010 J
VII- Exercice 7 : Valeur en eau d’un calorimètre
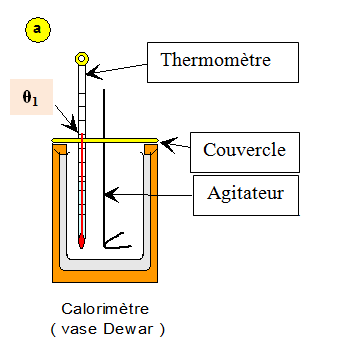
Un calorimètre est un récipient parfaitement isolé
qui permet d’éviter les transferts thermiques avec l’extérieur.
Un calorimètre contient un échantillon d’eau de
masse m1 = 95 g à la température θ1 = 20
° C.
Un échantillon d’eau de masse m2 =
71 g à la température θ2 = 50 ° C est alors ajouté.
Lorsque l’équilibre thermique est atteint, la
température finale θf est relevée.
La « valeur en eau » d’un corps est la masse d’eau
fictive μ qui a la même capacité thermique que le corps.
DONNÉE :
Capacité thermique massique de l'eau liquide : ceau
= 4,18 kJ . kg–1 . K–1.
a)-
Dans un premier temps, l’influence du calorimètre est négligée.
Déterminer la valeur de la variation d’énergie interne de chacun des
systèmes {Eau froide}, {Eau chaude} et {Eau froide ; Eau chaude}.
b)- En déduire la température finale θf de l’eau dans le calorimètre.
c)- La mesure donne θf = 31,2 ° C. Commenter ce résultat.
d)- Reprendre les raisonnements précédents en prenant en compte l’influence du calorimètre. En déduire la capacité thermique du calorimètre et sa valeur en eau.
a)-
Valeur de la variation d’énergie interne de chacun
des systèmes {Eau froide}, {Eau chaude} et {Eau froide ; Eau chaude}.
-
À l’équilibre thermique, la température
finale : θf.
-
Cas du système {Eau froide} :
-
ΔUEau froide = m1 . ceau
. (θf – θ1)
-
Cas du système {Eau chaude} :
-
ΔUEau chaude = m2 . ceau
. (θf – θ2)
-
Cas du système {Eau chaude ; Eau Froide} :
-
ΔUEau chaude + froide = m2 . ceau
. (θf – θ2) + m1
. ceau .
(θf – θ1)
-
Relation que l’on peut ordonner :
-
ΔUEau chaude + froide =
(m1 +
m2) . ceau
. θf – m1
. ceau .
θ1 – m2
. ceau .
θ2
b)-
Température finale
θf de l’eau dans le
calorimètre.
-
Le système {Eau froide ; Eau chaude} est un
système isolé.
-
L’énergie gagnée par le système {Eau
froide} a été perdue par le système {Eau chaude}.
-
ΔUEau chaude + froide =
0
-
(m1
+ m2) . ceau
. θf – m1
. ceau .
θ1 – m2
. ceau .
θ2 = 0
-
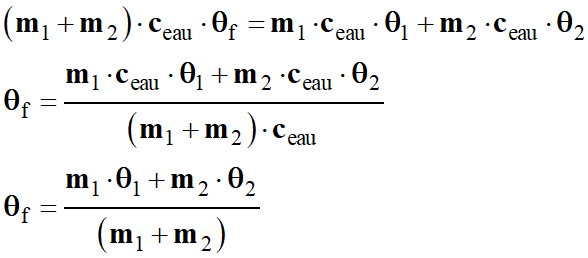
-
Application numérique :
-
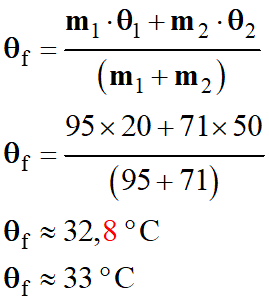
c)-
Commentaire du résultat.
-
La mesure donne
θf = 31,2 ° C.
-
La mesure finale est plus faible que celle
calculée.
-
Cette différence est liée au fait qu’une
partie de l’énergie cédée par l’eau chaude sert à chauffer les parois
intérieures du calorimètre, les différents éléments présents dans le
calorimètre (thermomètre, agitateur)
d)-
Capacité thermique du calorimètre et sa valeur en
eau.
-
En considérant que l’intérieur du calorimètre
et les différents éléments présents sont à la température θ1.
-
On considère que le système
S = {Eau froide ; Eau chaude ; Calorimètre} est isolé.
-
ΔUS =
0
-
ΔUS = ΔUEau
froide + ΔUEau
chaude + ΔUCalorimètre
= 0
-
m2 . ceau
. (θf
– θ2)
+ m1 . ceau
. (θf
– θ1)
+ Ccalorimètre
. (θf
– θ1)
= 0
-
Ccalorimètre .
(θf – θ1)
= – m2 .
ceau .
(θf
– θ2)
– m1 . ceau
. (θf
– θ1)
-
Ccalorimètre .
(θf – θ1)
= m2 . ceau
. (θ2
– θf)
+ m1 . ceau
. (θ1
– θf)
-
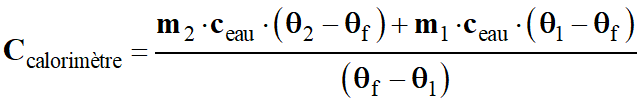
-
Capacité thermique du calorimètre :
-

-
Valeur en eau du calorimètre :
-
La valeur en eau d'un calorimètre correspond
à la masse d'eau ayant la même capacité calorifique que le calorimètre vide.
-
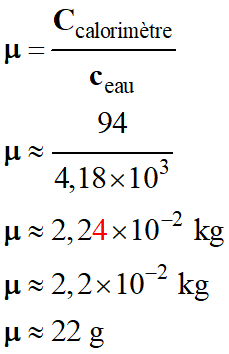
Mesure de la
capacité thermique massique du laiton.
VIII- Exercice 8 : Étude énergétique d'une centrale nucléaire
Une centrale nucléaire est le lieu de nombreux
transferts d'énergie dans lesquels l'eau joue un rôle important.
DOC. 1
Principe de fonctionnement d’une centrale nucléaire.
DONNÉES :
►
Capacité thermique massique de l’eau dans différentes conditions.
|
Température
( en ° C) |
Pression
(en bar) |
État |
cpm
(en J . K–1
. kg–1) |
|
270 |
155 |
Liquide |
5250 |
|
10 |
1 |
Liquide |
4180 |
|
270 |
56 |
Gazeux |
3800 |
- Puissance électrique fournie par la centrale nucléaire : Pe = 900 MW
-
Rendement de la centrale nucléaire : η = 33 %
►
Diagramme présentant les états de l’eau en fonction de la température et de la pression.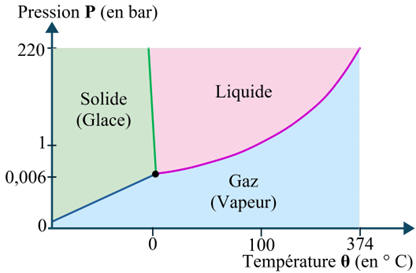
Questions
1.
Transferts d’énergie dans le circuit primaire :
a)- Calculer l'énergie fournie chaque seconde par le réacteur nucléaire et préciser le mode de transfert thermique par lequel cette énergie est échangée avec l’eau du circuit primaire.
b)- En analysant les données, justifier le choix d'utiliser de l'eau liquide dans le circuit primaire ainsi que de travailler à haute pression.
2. Transferts d'énergie dans le circuit secondaire.
L’énergie fournie par le réacteur nucléaire est
supposée intégralement transférer au circuit primaire puis au circuit
secondaire.
a)- Schématiser les différents transferts d'énergie liés au système {Eau du circuit secondaire}.
Préciser le signe de chacun des transferts représentés sur ce schéma.
b)-
Comment varie l'énergie interne
U du système {Eau du circuit
secondaire}au cours d'un cycle ?
c)-
Montrer que le flux thermique entre le circuit
secondaire et le circuit de refroidissement vaut 1,8 GW.
3.
Transfert d’énergie dans le circuit de
refroidissement.
L’eau du fleuve est récupérée par pompage, puis envoyée dans la canalisation avec un débit volumique constant Dv = 60 m3 . s–1.
La température de l’eau du fleuve à l’entrée du circuit de refroidissement est θe = 19 ° C.
Déterminer la température de l’eau à la sortie θs
de la canalisation.
1.
Transferts d’énergie dans le circuit primaire :
a)-
Énergie fournie chaque seconde par le réacteur
nucléaire et mode de transfert thermique.
-
Puissance électrique fournie par la centrale
nucléaire : Pe = 900 MW
-
Rendement de la centrale nucléaire : η
= 33 %
-
Énergie fournie chaque seconde par le
réacteur nucléaire :
-
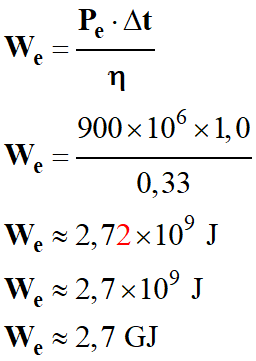
-
Circuit primaire :
-
Cuve du réacteur : les réactions nucléaires
qui ont eu lieu dans la cuve du réacteur produisent de l’énergie qui est
transférée à de l’eau liquide sous haute pression.
-
Cette énergie est transférée à l’eau du
circuit primaire par rayonnement.
b)-
Choix d'utiliser de l'eau liquide dans le circuit
primaire ainsi que de travailler à haute pression.
►
Capacité thermique massique de l’eau dans
différentes conditions.
|
Température
( en ° C) |
Pression
(en bar) |
État |
cpm
(en J . K–1
. kg–1) |
|
270 |
155 |
Liquide |
5250 |
|
10 |
1 |
Liquide |
4180 |
|
270 |
56 |
Gazeux |
3800 |
- La capacité thermique de l’eau à l’état liquide sous haute pression (5250 J . K–1 . kg–1) est supérieure à la capacité thermique
de l’eau à l’état gazeux sous haute pression (3800 J
. K–1 . kg–1).
-
Il est préférable de travailler avec de l’eau
à l’état liquide.
2.
Transferts d'énergie dans le circuit secondaire.
-
L’énergie fournie par le réacteur nucléaire
est supposée intégralement transférer au circuit primaire puis au circuit
secondaire.
a)-
Schéma des différents transferts d'énergie liés au
système {Eau du circuit secondaire}.
-
Schéma énergétique :
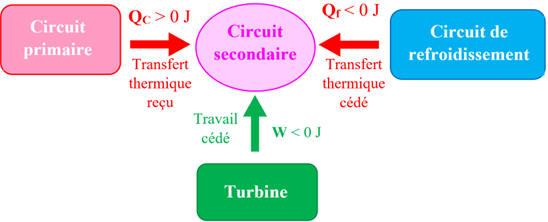
-
Transfert thermique reçu du circuit
primaire : QC > 0 J
-
Transfert thermique cédé au circuit de
refroidissement : Qf <
0 J
-
Travail cédé à la turbine :
W < 0 J
-
La vapeur d’eau entraîne le mouvement d’une
turbine reliée à un alternateur électrique.
b)-
Variation de l'énergie interne
ΔU du système {Eau du
circuit secondaire}au cours d'un cycle :
-
L’eau est condensée au contact d’un
refroidisseur (eau d’une rivière, d’un fleuve ou de la mer)
-
Elle revient au générateur de vapeur dans son
état initial pour reprendre un cycle.
-
En conséquence, au cours d’un cycle, la
variation ΔU du système
{Eau du circuit secondaire} est nulle.
-
ΔU
= 0
-
Application du premier principe de la
thermodynamique
-
ΔU
= QC +
Qf + W = 0
c)-
Valeur du flux thermique entre le circuit secondaire
et le circuit de refroidissement.
-
ΔU
= QC +
Qf + W = 0
-
Avec :
QC ≈ 2,7 GJ
-
D’autre part :
-
Puissance électrique fournie par la centrale
nucléaire : Pe = 900 MW
-
On peut calculer le travail cédé
W par le circuit secondaire à la
turbine par seconde :
-
W
= – Pe .
Δt
-
W
= – 900 × 1,00
-
W
≈ – 900 MJ
-
W
≈ – 0,900 GJ
-
Valeur du flux thermique :
-
QC
+ Qf +
W = 0
-
Qf
= – QC –
W
-
Qf
≈ – 2,7 + 0,900
-
Qf ≈ – 1,8 GJ
-
Ce résultat est bien en accord avec celui
donné dans l’énoncé.
3.
Transfert d’énergie dans le circuit de
refroidissement.
-
Température de l’eau à la sortie θs
de la canalisation.
-
L’eau du fleuve est récupérée par pompage,
-
Elle est envoyée dans la canalisation :
-
Débit volumique constant Dv
= 60 m3 . s–1.
-
La température de l’eau du fleuve à l’entrée
du circuit de refroidissement :
-
θe = 19 ° C.
-
Masse volumique de l'eau liquide dans les
conditions de l'étude :
-
ρeau = 1000 . kg
. m–3
-
Volume de l’eau par seconde :
-
V
= 60 m3
-
Chaque seconde, l’énergie fournie à l’eau est
de 1,8 GJ.
-
Variation de l’énergie de l’eau :
-
ΔUeau
= m . ceau . (θs
– θe)
-
Température de l’eau à la sortie θs
de la canalisation :
-

-
Application numérique :
-
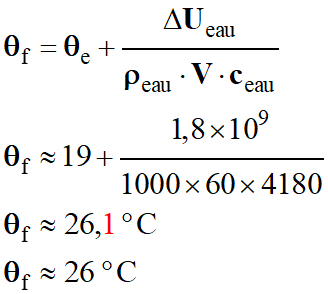
-
Ces rejets thermiques sont strictement
encadrés pour minimiser leur impact sur l'environnement.
-
Les centrales nucléaires doivent respecter
des réglementations strictes pour minimiser ces impacts et surveiller en
permanence la température de l’eau rejetée.