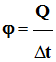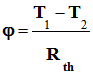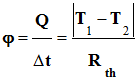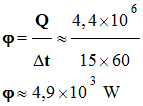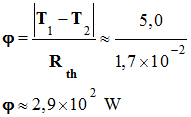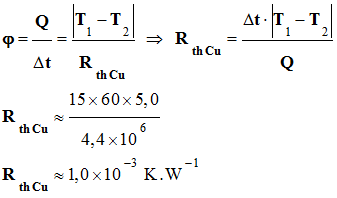|
Chap. N° 14 |
Transferts macroscopiques d'énergie. Cours. |
|
|
|
|
|
|
Exercices : énoncé avec correction
a)- Exercice 8 page 364 : Prendre conscience de la valeur de
NA.
b)- Exercice 11 page 364 : Connaître la relation entre
ΔU et
c.
c)- Exercice 12 page 364 : Calculer la variation d’énergie interne d’un
système.
d)- Exercice 15 page 365 : Illustrer des modes de transferts thermiques.
e)-
Exercice 18 page 365 : Calculer une énergie thermique transférée.
f)- Exercice 22 page 366 : Calculer une variation de température.
g)-
Exercice 23 page 366 : Une ou plusieurs couches ?
h)- Exercice 29 page 368 : Un isolant, la laine de verre.
i)- Exercice 34 page 370 : Que calor. |
I- Du
microscopique au macroscopique.
-
L’échelle de l’infiniment petit,
appelée échelle microscopique permet d’étudier les atomes, les
molécules et les ions.
-
Elle permet de considérer un
atome de fer :
-
Masse d’un atome :
mFe
≈ 9,3
× 10–23 g.
-
À l’échelle humaine (notre
échelle), c’est-à-dire l’échelle macroscopique, on considère un
morceau de fer de quelques grammes.
► Exemple :
-
Si l’on veut réaliser la
combustion du fer dans le dioxygène au laboratoire, on peut
utiliser un morceau de fil de fer de quelques grammes.
- On ne travaille pas à l’échelle de l’atome.
- On travaille à notre échelle, à l’échelle humaine,
l’échelle macroscopique.
► Question :
-
quel est le
nombre d’atomes de fer N contenus dans un échantillon de
fer de masse m = 3,5 g ?
-
Nombre d’atomes de fer contenus
dans l’échantillon :
-
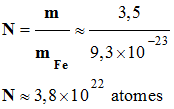 .
.
-
Conclusion : cette valeur est
considérable !!!
-
Que représente ce nombre
N ?
-
ce nombre
représente une quantité de matière.
-
En chimie, la quantité de matière
représente un nombre d’entités chimiques, c’est-à-dire, un
nombre d’atomes, de molécules ou d’ions.
-
Pour compter un grand nombre
d’objets, on les regroupe en paquets.
-
Il existe beaucoup d’exemples :
les œufs par douzaines, les chaussettes par paires, les rames de
papier par 500 feuilles, les bouteilles par six ou douze, …
-
Les entités chimiques comme, les
atomes, les molécules et les ions, se comptent aussi par paquet.
-
On appelle mole un paquet
d’entités chimiques toutes identiques.
-
La mole est la réunion d'un
nombre déterminé d’entités chimiques toutes identiques.
- Une quantité de référence a été choisie arbitrairement.
- Elle est donnée par le
Journal officiel
du 23 décembre 1975.
- On note : NA le nombre d’entités dans un paquet.
- Un tel paquet porte le nom de mole.
- La mole est une unité de quantité de matière de symbole :
mol.
|
Définition de la mole : - La mole est la quantité de matière d'un système contenant autant d'entités élémentaires qu'il y a d'atomes dans - Si l'on prend une mole d'atomes de carbone 12, la masse correspondante est de Le paquet comprend
NA
atomes de carbone 12. |
-
La détermination de la valeur de
NA fut un grand défi pour la science.
3)- La
Constante d’Avogadro NA.
-
Le nombre NA
est défini par la relation suivante :
-
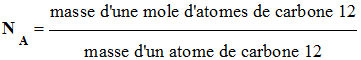
- Par définition, on connaît la masse d’une mole atomes de carbone 12.
-
mais, on a
longtemps ignoré les valeurs de NA et de la
masse d’un atome de carbone 12.
-
On doit à Jean Perrin la première
détermination de NA en 1923.
-
Le nombre NA a
été appelé constante d’Avogadro, en hommage à Avogadro, célèbre
chimiste et physicien italien (1776 – 1856).
-
Le nombre NA
représente le nombre d’entités élémentaires par mol, on
l’exprime en mol–1.
-
Des mesures récentes indiquent
qu’il y a : 6,022137
× 1023 atomes de carbone 12 dans
- On arrondit cette valeur.
- On écrit :
-
NA
≈ 6,02
× 1023 mol–1
► Conséquence :
-
Une mole, est un paquet de 6,02
× 1023 entités chimiques identiques.
► Exemples :
-
Une mole d’atomes de fer contient
6,02
× 1023 atomes de fer.
-
Une mole de molécules d’eau
contient 6,02
× 1023
molécules d’eau.
-
Une mole d’électrons contient
6,02
× 1023
électrons
-
Une mole d’ions chlorure contient
6,02
× 1023
ions chlorure.
![]() La
constante d’Avogadro fait le lien entre les échelles
microscopique et macroscopique.
La
constante d’Avogadro fait le lien entre les échelles
microscopique et macroscopique.
II- Variation de l’énergie interne d’un système.
► Échelle microscopique :
-
À l'échelle microscopique, les
particules constituant le système sont animées de mouvements
individuels.
-
Cette agitation augmente avec la
température, on l'appelle l'agitation thermique.
-
Plus la température d’un système
est élevée, plus l’agitation thermique des particules qui le
constituent est grande et plus son énergie cinétique
microscopique est grande.
-
Au niveau microscopique, à toute
liaison entre deux particules du système est associée une
énergie potentielle microscopique.
-
L’énergie potentielle
microscopique est due aux interactions gravitationnelle,
électromagnétique, forte et faible entre les particules qui
constituent le système.
-
On distingue les énergies
potentielles microscopiques chimique, électrique, magnétique et
nucléaire.
-
L’énergie interne est la somme
des énergies cinétique et potentielle microscopiques, c’est
l'énergie liée à sa structure interne microscopique, notée U.
► Échelle macroscopique :
-
L’énergie mécanique
Em
d’un système macroscopique résulte de contributions
macroscopiques.
-
L’énergie mécanique d’un système
est la somme de son énergie cinétique et de son énergie
potentielle.
-
Relation :
-
Em
= EC
+ EP.
-
Unité : joule (J)
► Énergie totale d’un système :
-
L’énergie totale d’un système est
la somme de son énergie interne et de son énergie mécanique.
-
Etot
= Em
+ U
2)-
Variation d’énergie d’un système.
a)- Variation de l’énergie totale
d’un système.
-
La variation d’énergie totale du
système est la somme de la variation de son énergie interne et
de la variation de son énergie mécanique :
-
ΔEtot
=
ΔEm
+
ΔU
b)-
Cas : l’énergie mécanique du
système est constante.
-
Lorsque l’énergie mécanique du
système se conserve, la variation d’énergie totale du système
est due uniquement à la variation de son énergie interne.
-
Si
ΔEm
= 0
-
ΔEtot
=
ΔU
c)- Variation d’énergie interne :
-
La variation d’énergie interne
ΔU d’un système est la conséquence d’échanges
d’énergie avec l’extérieur par travail
W ou par transfert
thermique Q.
-
Si l’énergie mécanique du système
est constante :
ΔEm
= 0
-
ΔEtot
=
ΔU
= W +
Q
-
Le travail W et le
transfert thermique Q sont des modes de transfert
d’énergie.
-
Leur signe dépend du sens du
transfert entre le système et le milieu extérieur.
![]() Par
convention :
Par
convention :
-
Le travail et le transfert
thermique sont comptés positivement s’ils sont reçus par le
système.
-
Le travail et le transfert
thermique sont comptés négativement s’ils sont cédés par le
système.
d)-
Exemple de convertisseurs
d’énergie.
-
Le radiateur électrique convertit
de l’énergie électrique en énergie thermique.
-
Le système (Radiateur électrique)
reçoit un travail électrique :
W
> 0
-
Le système (Radiateur électrique)
cède un transfert thermique :
Q
< 0
► Transfert par chaleur produisant
une élévation de température (sans changement d’état) :
-
La variation d’énergie interne
d’une masse m de substance dont la température varie
d’une valeur initiale
θi
à une valeur finale
θf,
sans changement d’état, est donnée par la relation suivante :
|
ΔU
= m . c . (θf
-
θi
) = m .
c .Δθ |
|
ΔU
en joule (J) |
|
m en
kilogramme (kg) |
|
c
capacité thermique massique
(J.kg
– 1.°
C– 1)
|
|
θf
-
θi
températures en (°C)
ou (K) |
► Remarque 1 :
-
On peut travailler avec la
température absolu T en kelvin (K)
|
ΔU
= m . c . (Tf
-
Ti
) = m .
c .ΔT |
|
ΔU en joule (J) |
|
m en
kilogramme (kg) |
|
c
capacité thermique massique
(J.kg
– 1.°
C– 1) ou (J.kg
– 1.K–
1) |
|
Tf
-
Ti
températures absolues
en (K)
(kelvin) |
► Remarque 2 :
- ΔT
= Δθ
► Remarque 3 :
-
La capacité thermique massique
c d’une substance correspond au transfert thermique
nécessaire pour faire varier de 1 ° C (ou 1 K) une masse de
-
Unité : (J.kg
– 1.° C–
1) ou (J.kg
– 1.K– 1)
► Exemple :
- Calculer la quantité de chaleur
nécessaire pour obtenir
- On donne : masse volumique de
l’eau :
ρ =
- Quantité de chaleur nécessaire :
- ΔU
= Q = m . c . ( θf
–
θi
)
=>
Q =
80
×
4,18
×
(80 – 20)
=> Q =
2,0
×
10 4 kJ.
► Remarque 4 :
-
Si
θf
>
θi
=>
ΔU = Q
> 0, la substance reçoit de l'énergie du milieu extérieur.
-
Si
θf
<
θi
=>
ΔU = Q
<
0, la substance cède de l'énergie au milieu extérieur.
III- Les
modes de transferts thermiques.
1)- Les
différents modes de transferts.
-
Si l'on chauffe l'extrémité d'une
barre métallique, on remarque que la température de l'autre
extrémité augmente très vite.
-
Les particules de la partie
chaude communiquent une partie de l'agitation thermique aux
particules voisines et ainsi de suite.
-
L'agitation thermique se transmet
de proche en proche de la région chaude vers la région froide
sans transport de matière.
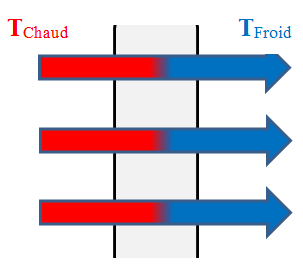
-
La conduction se produit
principalement dans les solides
-
Dans les fluides, le transfert de
chaleur se fait grâce aux courants de convection.
-
Exemple :
- L'air chaud est plus léger que l'air froid.
- L'air chaud s'élève et en s'élevant, se refroidit
en échangeant de l'énergie avec les couches supérieures.
-
Le transfert par convection se
fait avec transfert de matière.
-
La convection se produit
principalement dans les fluides (liquides et gaz).
- L'énergie transportée sous forme de radiations électromagnétiques est appelée énergie rayonnante.
- Elle est notée
WR. Elle s'exprime en joule
(J).
-
Tout corps chaud émet des
radiations électromagnétiques qui transportent de l'énergie.
-
Le rayonnement ne nécessite pas
de milieu matériel, il s’effectue même dans le vide.

2)- Flux
et résistance thermique.
a)- Définition du flux thermique :
-
On considère un matériau dont les
deux faces parallèles numérotées 1 et 2, de même surface
S,
sont à des températures différentes T1 et
T2,
telles que T1 >
T2.
-
La paroi plane, dont deux faces
sont à des températures différentes T1 et
T2,
est le siège d’un transfert thermique par conduction.
-
La capacité d’un matériau, à
réaliser plus ou moins rapidement ce transfert, est liée à sa
résistance thermique Rth.
-
L’énergie Q est transférée
de la face 1 vers la face 2 pendant la durée
Δt.
-
Le flux thermique
φ
(phi) traversant ce matériau est alors défini par la relation :
|
|
|
Énergie thermique transférée :
Q
en joule (J) |
|
Durée :
Δt ne seconde (s) |
|
Flux thermique :
φ en
watt : (J . s–1 = W) |
-
Le flux thermique a la dimension
d’une puissance : C’est une énergie par unité de temps.
-
Le flux thermique est l’énergie
transférée à travers une paroi par unité de temps.
-
Ce transfert se fait spontanément
de la source chaude vers la source froide.
-
Ce transfert est naturellement
irréversible.
-
Si l’écart de température
T1
– T2 est maintenu constant, le flux thermique
est donné par la relation suivante :
|
|
|
Températures absolues :
T1 et
T2
en kelvin (K) |
|
Résistance thermique :
Rth unité : ?
à déterminer |
|
Flux thermique :
φ en
watt : (J . s–1 = W) |
-
En quelle unité s’exprime la
résistance thermique Rth ?
-
La résistance thermique s’exprime
en (K . W–1) ou (° C . W–1).

-
Remarque :
-
Plus la résistance thermique du
matériau est élevée, plus le flux thermique est faible à travers
le matériau.
-
Ce dernier empêche le transfert
d’énergie à travers lui ; C’est un bon isolant thermique.
-
Un matériau qui a une résistance
thermique élevée est un bon isolant thermique.
c)- Exercice 17 page 365 : Calculer
et exploiter un flux thermique
|
On peut trouver sur le marché
des casseroles en aluminium et d’autres en cuivre. Pour déterminer lequel de ces deux matériaux est celui qui transfère l’énergie thermique le plus rapidement, Marc utilise deux
plaques de mêmes dimensions, l’une en cuivre et
l’autre en aluminium. Il maintient un écart de
température constant et égal à 5,0 ° C entre les
deux faces planes et parallèles de la plaque de
cuivre. Le transfert thermique, pendant une durée Δt = 15 min, entre les deux faces est : QCu
= 4,4
× 106 J. Ensuite, il procède de même avec la plaque d’aluminium dont la résistance thermique est Rth
Al = 1,7
× 10–2 K . W–1. -
Donnée le flux
thermique a pour expression : -
-
Quel est le flux
thermique qui traverse la plaque de cuivre ? -
Quel est le flux
thermique qui traverse la plaque d’aluminium ? -
Pour des dimensions
identiques, quel est le matériau qui transfère le
plus rapidement l’énergie thermique ? |
|
► Flux thermique qui
traverse la plaque de cuivre : -
Pour la plaque de
cuivre, on donne : - Le transfert thermique, pendant une durée Δt = 15 min, entre les deux faces est : - QCu = 4,4
× 106 J -
► Flux thermique qui
traverse la plaque d’aluminium : -
On donne : |T1
– T2| = 5,0° C = 5,0 K et Rth
Al = 1,7
× 10–2 K . W–1 -
► Matériau qui
transfère le plus rapidement
l’énergie thermique : -
On peut comparer les
valeurs des deux résistances thermiques : -
Résistance thermique
de la plaque de cuivre : -
- Résistance thermique de la plaque d’aluminium : - Rth Al
= 1,7
× 10–2 K . W–1 -
Rth Al
> Rth Cu -
Le cuivre transfère
mieux l’énergie thermique que l’aluminium. -
Ou, l’aluminium est
un meilleur isolant que le cuivre. |
d)-
Résistance thermique
Rth
et conductivité thermique
λ d’un matériau.
-
La résistance thermique
Rth
d’une paroi dépend :
-
De la conductivité thermique
λ du
matériau ;
-
De son épaisseur
e ;
-
Et de la surface
S
traversée par le flux.
-
Elle est proportionnelle à
l’épaisseur e
et inversement proportionnelle à la
conductivité thermique
λ
et à la surface S.
-
Relation :
|
|
|
Épaisseur :
e en mètre (m) |
|
Surface :
S en (m2) |
|
Conductivité thermique du
matériau :
λ en (W
. m–1 . K–1) |
|
Résistance thermique :
Rth
en (K . W–1) ou (° C . W–1) |
-
La conductivité thermique
caractérise un matériau :
► Exemples :
|
Matériau |
λ (W . m–1
. K–1) |
|
Cuivre |
400 |
|
Aluminium |
250 |
|
Verre |
1 |
|
Béton |
1 |
|
Bois |
0,1 |
► Cas de plusieurs parois
accolées :
-
Lorsque plusieurs parois sont
accolées, la résistance thermique totale
Rth tot
est égale à la somme des résistances thermiques de chaque paroi.
-
Relation :
-
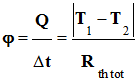
-
Avec : Rth tot
= Rth1 +
Rth2 +
Rth3
+ Rth4 + …
IV- Établissement
d’un bilan énergétique.
► Pour établir un bilan
énergétique, il faut :
-
Définir le système macroscopique
étudié ;
-
Relever la nature des transferts
énergétiques (par travail ou par transfert thermique) entre le
système et le milieu extérieur ;
-
Repérer le sens des transferts et
leur attribuer un signe positif si le système reçoit de
l’énergie ou négatif si le système cède de l’énergie.
2)-
Exemple : exercice 19 page 366 : Établir un bilan énergétique.
|
Un cumulus électrique est une réserve d’eau chauffée par un conducteur ohmique. En
l’absence de chauffage, la température de l’eau
chaude qu’il contient diminue au fil des heures. On souhaite faire le bilan
énergétique de l’eau contenue dans le cumulus. -
Définir le système
étudié. -
Relever la nature des
transferts énergétiques entre le système et le
milieu extérieur. -
Repérer
le sens des transferts et leur attribuer un
signe. -
Présenter le bilan
énergétique à l’aide d’un schéma. |
|
► Système étudié :
S -
S = {Eau
contenue dans le cumulus}
► Nature des transferts
énergétiques entre le système
et le milieu
extérieur. - La résistance du cumulus, lorsqu’elle est traversée par un courant électrique, transfère à l’eau de l’énergie
électrique par travail électrique We. -
La température de
l’eau contenue dans le cumulus augmente. - Lorsque la résistance n’est plus traversée par un courant électrique, la
température de l’eau diminue lentement. -
Le système S cède de
l’énergie au milieu extérieur sous forme d’énergie
thermique Q.
► Sens des transferts
et signe : - L’eau reçoit de l’énergie par travail électrique We. - Cette énergie est comptée positivement : We
> 0. - L’eau cède de l’énergie Q par transfert thermique. - Cette
énergie est comptée négativement : Q < 0.
► Schéma du bilan
énergétique : |
1)- QCM :
pour chaque question indiquer la (ou les) bonne(s) réponse(s).
|
|
2)-
Exercices :
a)-
Exercice 8 page 364 : Prendre
conscience de la valeur de NA.
b)-
Exercice 11 page 364 : Connaître
la relation entre
ΔU et
c.
c)-
Exercice 12 page 364 : Calculer
la variation d’énergie interne d’un système.
d)-
Exercice 15 page 365 : Illustrer
des modes de transferts thermiques.
e)-
Exercice 18 page 365 : Calculer
une énergie thermique transférée.
f)-
Exercice 22 page 366 : Calculer
une variation de température.
g)-
Exercice 23 page 366 : Une ou
plusieurs couches ?
h)-
Exercice 29 page 368 : Un
isolant, la laine de verre.
i)-
Exercice 34 page 370 : Que calor.
|
|