|
Applications des lois de Newton et de Kepler. Cours. |
|
|
|
|
|
|
Exercices : a)-
Exercice 9 page 172 :
Étudier le lancer du poids. b)- Exercice 10 page 173 :
Faire une analyse dimensionnelle. c)- Exercice 17 page 174 :
Étude du canon à électrons. d)-
Exercice 18 page 175 :
Neptune et Galatée.
e)-
Exercice 20 page 176 :
Poids et force électrostatique. f)- Exercice 21 page 176 : De
l’optique avec des électrons. g)- Exercice 22 page 177 :
Quelle est la masse de Jupiter. h)- Exercice 26 page 179 :
Principe du spectromètre de masse. |
I-
Mouvement d’un
système S dans un champ uniforme.
1)- Cas
d’un objet dans un champ de pesanteur uniforme.
-
Une balle de tennis de masse
m est lancée d'un
point O
avec une vitesse initiale
faisant un angle
α
avec l'horizontale.
-
On considère que la balle se déplace dans un champ de
pesanteur uniforme.
-
Données :
v0 =12
m / s ; α =
60 ° ; m =
50
g
et g
= 9,81
m / s².
-
On choisit comme repère
:
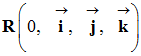y'Oy
axe vertical orienté vers le haut et
x'Ox axe horizontal
orienté de gauche à droite.
-
Le plan
(x'x, y'y) contient le vecteur vitesse
.
-
L’axe
z'Oz est orthogonal au plan
(x'x, y'y).
-
Les vecteurs forment un trièdre direct.
-
On choisit comme origine des espaces le point
O et
l'origine des dates l'instant ou la balle occupe la position
O.
-
Schéma à l’instant
t :
-
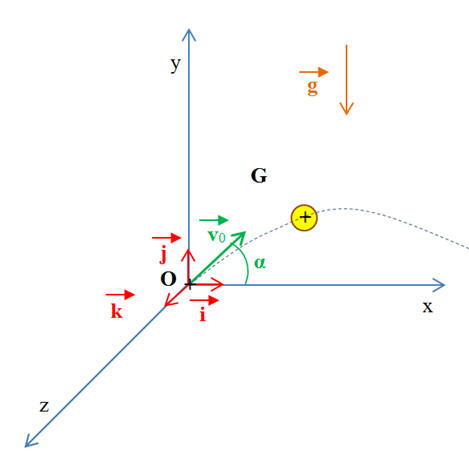
Donner les équations horaires du mouvement.
-
Que peut-on dire du mouvement de
G suivant l'axe
x'Ox, suivant l'axe
y'Oy ?
-
Dans quel plan s'effectue le mouvement de
G ?
-
Déterminer l'équation de la trajectoire du point
G.
Conclusion.
b)-
Les différentes étapes de l’étude :
►
Première étape : Définition du système :
- On précise le système étudié : dans le cas présent une balle de masse m, assimilable à un point matériel G :
- Système : S (m, G)
►
Deuxième étape : Choix du référentiel d’étude et
on indique les conditions initiales :
-
Dans le cas présent, on étudie le mouvement d’une balle
dans un champ de pesanteur uniforme.
-
Le mouvement a lieu au voisinage du sol.
-
On choisit un référentiel terrestre supposé galiléen.
-
À ce référentiel, on associe un repère d’espace
orthonormé.
-
L’ensemble est noté :
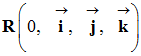
- Le plus souvent, le référentiel d’étude et le repère d’espace lié au référentiel sont donnés dans l’énoncé.
-
Conditions initiales :
Position et vitesse du mobile au temps
t = 0 s
|
|
|
►
Troisième étape : Étude dynamique :
-
Bilan des forces : Inventaire des actions mécaniques que
subit le système
-
Avec quoi le système est-elle en interaction ?
-
Interaction avec la Terre (champ de pesanteur uniforme) :
-
La balle est soumise à son poids
.
-
La balle est en interaction avec l’air qui l’entoure.
-
On peut négliger la poussée d’Archimède et les forces de
frottements.
-
On peut donner les coordonnées des différentes forces et
vecteurs dans le repère choisi :
|
|
|
-
Application de la deuxième loi de Newton :
|
D
alors la somme vectorielle de ces forces est égale à la dérivée
par rapport au temps de son vecteur quantité de mouvement : -
On écrit : -
|
-
Comme la masse m de la balle ne varie pas au cours
du temps, on peut en déduire la relation suivante :
-
-
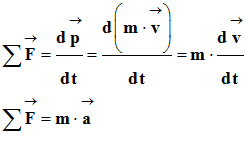
D’où :
-
►
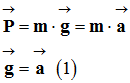
Quatrième étape : Étude cinématique.
-
On peut donner les coordonnées du vecteur accélération
dans le repère d’étude :
|
|
et |
|
|
De l’équation
(1), on tire |
||
 |
||
-
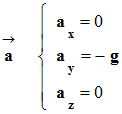Le but est de trouver les équations horaires du vecteur
vitesse et du vecteur position de la balle.
De
l’accélération à la vitesse :
-
On utilise la relation :
-
-
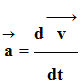
Le vecteur accélération
est
la dérivée par rapport au temps du vecteur vitesse
.
-
La détermination du vecteur vitesse nécessite de
rechercher la primitive par rapport au temps de chaque
coordonnée du vecteur accélération en tenant compte des
conditions initiales.
-
On cherche les primitives des équations précédentes.
-
Il apparaît des constantes qui sont liées aux conditions
initiales.
|
|
|
D’après les conditions
initiales |
 |
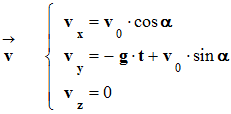De
la vitesse à la position.
-
On opère de la même façon :
-
-
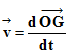
Le vecteur vitesse
est la
dérivée par rapport au temps du vecteur position
.
-
La détermination du vecteur position nécessite de
rechercher la primitive par rapport au temps de chaque
coordonnée du vecteur vitesse en tenant compte des conditions
initiales.
|
|
|
D’après les conditions
initiales |
 |
-
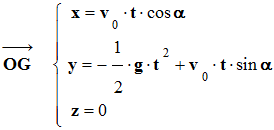Remarques :
-
Le mouvement suivant l'axe
x'Ox est rectiligne
uniforme.
-
Le mouvement suivant l'axe
y'Oy est rectiligne
uniformément varié.
-
Le mouvement de
G
est contenu dans le plan
(x'x, y'y) appelé plan de tir.
-
Il contient le vecteur
.
De
la position à la trajectoire.
-
La trajectoire d’un point est l’ensemble des positions
successives occupées par ce point au cours du temps.
-
On élimine le temps
t
pour trouver la relation entre les coordonnées
x et
y
du vecteur position.
-
Comme le mouvement a lieu dans le plan (xOy) :
-
y =
f
(x).
|
On en déduit
l’équation de la trajectoire |
|
|
- La trajectoire de
G
est une portion de parabole contenue dans un plan vertical
contenant le vecteur vitesse
.
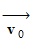- Elle est liée aux conditions initiales.
-
Chronophotographie et animation CabriJava.
2)- Cas
d’une particule chargée dans un champ électrostatique uniforme.
a)-
Le champ électrique uniforme.
1sph07.htm
-
Un champ électrique est dit uniforme dans une région de
l’espace si le vecteur champ
conserve en tout point de
cette région, la même direction, le même sens et la même valeur.
-
Un condensateur plan est formé par deux plateaux
conducteurs parallèles A
et B appelés
armatures, séparés par un isolant de faible épaisseur
d.
-
Dans l’espace situé entre les armatures, le champ
électrique :
-
Est considéré comme uniforme,
-
Sa direction est perpendiculaire aux armatures,
-
Son sens est dirigé de l’armature positive vers l’armature
négative (sens des potentiels décroissants),
-
Son intensité (sa valeur) : 
-
Un électron M de masse
m, porte la charge
électrique q =
– e.
-
L’électron M pénètre, dans le vide, avec le
vecteur vitesse
, faisant un
angle α avec l’horizontale à l'intérieur d'un
condensateur plan.
-
L’électron M coïncide avec
O à la date
t
= 0 s.
Appliquer l’étude précédente à l’électron.
-
Données : m = 9,1
x 10–31
kg ; Charge :
q = – e = – 1,6 x 10–19 C
-
E = 4,7
x 103 V / m ;
g = 9,81 N / kg
c)-
Les différentes étapes de l’étude :
►
Première étape : Définition du système :
-
Système S : électron
M de masse
m et
de charge q.
►
Deuxième étape : Référentiel d’étude et conditions
initiales :
-
Référentiel terrestre supposé galiléen
-
Le repère d’espace choisi :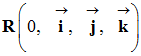
contient
le vecteur vitesse
et le
vecteur champ électrique
.
-
Position et vitesse du mobile au temps
t = 0 s
|
|
|
►
Troisième étape : Étude dynamique :
-
Bilan des forces : inventaire des forces extérieures
exercées sur l’électron.
-
Son poids
.
-
La force électrostatique
-
L’électron se déplace dans le vide, il n’y a pas
d’interaction avec l’air.
-
Comparaison de Fe et
P.
-
Fe =
e . E ≈ 1,6
x 10–19
x 4,7
x 103
-
Fe ≈ 7,5
x 10–19 N
-
P = m . g
≈ 9,1
x 10–31
x 9,81
-
P
≈ 8,9
x 10–30
N
-
-
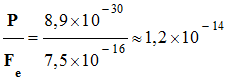
En conséquence, P <<
Fe,
on peut négliger les effets du poids devant celui de la force
électrostatique
Fe.
-
En conséquence, l’électron n’est soumis qu’à la force
électrostatique
.
-
Coordonnées des différentes forces et vecteurs dans le
repère choisi :
|
|
|
-
Application de la deuxième loi de Newton :
|
D
alors la somme vectorielle de ces forces est égale à la dérivée
par rapport au temps de son vecteur quantité de mouvement : -
On écrit : -
|
-
Comme la masse m de l’électron ne varie pas au
cours du temps, on peut en déduire la relation suivante :
-
-
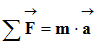
D’où :
-
►
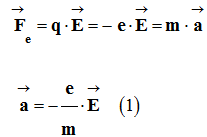
Quatrième étape : Étude cinématique.
-
On peut donner les coordonnées du vecteur accélération
dans le repère d’étude :
|
|
et |
|
|
De l’équation
(1), on tire |
||
 |
||
-
Ainsi par recherche des primitives, on retrouve les
coordonnées du vecteur vitesse et du vecteur position.
De
l’accélération à la vitesse :
|
|
|
D’après les conditions
initiales |
 |
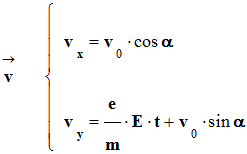De
la vitesse à la position :
|
|
|
D’après les
conditions initiales |
 |
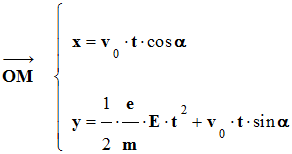De
la position à la trajectoire :
-
Équation de la trajectoire : on élimine le temps
t
entre x et
y pour exprimer
y
= f (x).
-
-
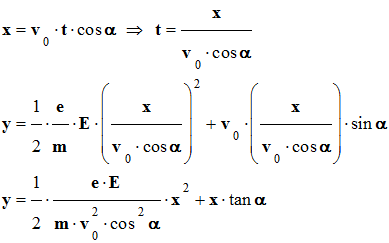
La trajectoire de l’électron est une portion de parabole.
-
Déviation d’un faisceau d’électrons (oscilloscope)
II-
Mouvement des
satellites et des planètes.
1)-
Description par la deuxième loi de Newton.
-
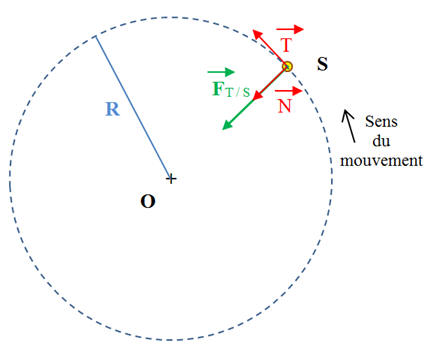
On étudie le mouvement d’un satellite
S, de masse
m, assimilé à un point matériel, en orbite autour de la
Terre de centre O et de masse
MT.
-
On considère que le satellite décrit une orbite
circulaire de rayon R =
OS.
Appliquer l’étude précédente au satellite
S.
b)-
Les différentes étapes de l’étude :
►
Première étape : Définition du système :
-
Système S : Satellite
S de masse
m.
►
Deuxième étape : Référentiel d’étude
-
Référentiel géocentrique supposé galiléen.
- Pour simplifier l’étude d’un tel mouvement et en déduire les caractéristiques, il faut utiliser le repère de Frenet :
- Repère mobile lié au satellite
-
-
: désigne un
vecteur unitaire tangent à la trajectoire et orienté dans le
sens du mouvement.
-
: désigne un
vecteur unitaire perpendiculaire à
et orienté vers le
centre O du cercle.
►
Troisième étape : Étude dynamique :
-
Bilan des forces : inventaire des forces extérieures
exercées sur le satellite.
-
Le satellite est en interaction avec la Terre : force
d’interaction gravitationnelle exercée par la Terre sur le
satellite : 
-
Le satellite est aussi en interaction avec les autres
astres de l’Univers : cette interaction est négligeable devant
celle exercée par la Terre.
-
Le satellite est en interaction avec l’atmosphère de la
Terre qui entraîne des forces de frottements.
-
Dans notre étude, on négligera cette interaction devant
celle exercée par la Terre.
-
On considère que le satellite n’est soumis qu’à la seule
force d’attraction gravitationnelle exercée par la Terre.
-
-
Application de la deuxième loi de Newton :
|
D
alors la somme vectorielle de ces forces est égale à la dérivée
par rapport au temps de son vecteur quantité de mouvement : -
On écrit : -
|
-
Comme la masse m du satellite ne varie pas au
cours du temps, on peut en déduire la relation suivante :
-
-
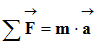
D’où :
-
-
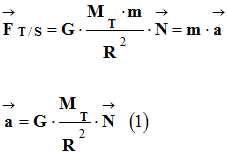
Le vecteur accélération est centripète, il est orienté
vers le centre de la trajectoire.
►
Quatrième étape : Étude cinématique.
-
Comme on est en présence d’un mouvement circulaire,
|
Vecteur accélération |
|
Le vecteur accélération
tangentielle |
Le vecteur accélération normale |
|
|
|
|
|
|
Direction |
Tangent à la trajectoire au point considéré |
Centripète |
|
|
Sens |
Orienté dans le sens du mouvement |
Orienté vers le centre du cercle |
|
|
Valeur |
C’est la dérivée par rapport au temps de la valeur de la vitesse
v |
|
-
D’autre part, la relation (1) indique que :
-
-
On en déduit que :
|
Vecteur accélération |
Relation |
|
|
|
-
De l’accélération à la vitesse :
-
-
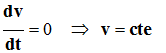
Le satellite est animé d’un mouvement circulaire
uniforme.
-
D’autre part :
-
-
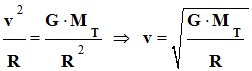
La valeur de la vitesse du satellite est indépendante de
sa masse.
-
Relation en fonction de l’altitude
h du satellite
-
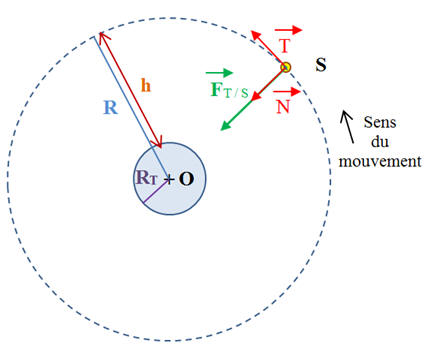
On note R =
R
T +
h, ou
h désigne l’altitude du satellite :
-
-
La vitesse du satellite diminue lorsque l’altitude
augmente.
-
Expression de la période T : Durée nécessaire pour
effectuer un tour :
-
-
La période de révolution d’un satellite est indépendante
de sa masse m, elle dépend entre autres du rayon de la trajectoire.
-
La période de révolution d’un satellite augmente avec le
rayon de sa trajectoire.
2)-
Description des lois de Kepler.
-
Pour Ptolémée (II
e siècle),
- Copernic est à l’origine du système héliocentrique (1543).
- Dans ce référentiel, les neuf planètes du système
solaire ont des trajectoires quasi circulaires dont le centre
est le Soleil.
-
Kepler (1571 – 1630) utilisant les travaux de son maître
Tycho Brahe (1546 – 1601) formule les trois lois qui décrivent
le mouvement des planètes autour du Soleil.
b)-
Première loi : la loi des trajectoires
Dans
le référentiel héliocentrique, la trajectoire du centre d’une
planète est une ellipse dont le Soleil est l’un des foyers.
-
Remarque : le cercle est une ellipse dont les deux foyers
sont confondus avec le centre.
-
Définition d’une ellipse :
-
Une ellipse est l’ensemble des points dont la somme des
distances à deux points fixes
F et
F’ (les foyers)
est une constante :
r1
+
r2
=
-
Le grand axe de l’ellipse est égal à
-
La distance entre les deux foyers est 2
c.
-
Schéma :
|
|
 |
c)-
Deuxième
loi : Loi des aires.
Le
segment de droite qui relie le centre du Soleil au centre de la
planète balaie des aires égales pendant des durées égales.
-
Il résulte de ceci que la planète se déplace plus vite
lorsqu’elle se rapproche du Soleil.
-
En toute rigueur, le mouvement d’une planète n’est pas
uniforme.
|
|
 |
d)-
Troisième loi : Loi des périodes.
Pour
toutes les planètes, le rapport entre le cube du demi-grand axe
a de la trajectoire et le carré de la période
T de
révolution est la même :
-
.
-
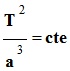Cette constante ne dépend pas de la masse de la planète.
- Si la trajectoire est un cercle de rayon R, on peut écrire que :
-
.
-
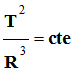Cette constante peut être calculée.
-
Exemple :
-
Dans le cas du système solaire, on peut donner
l’expression de la période de révolution d’une planète du
système solaire :
-
-
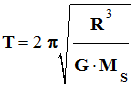
En élevant cette expression au carré et en ordonnant, on
peut écrire :
-
-
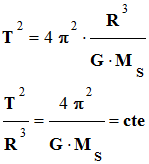
La constante s’identifie à 
.
-
En conséquence, on peut déterminer la masse du Soleil à
partir de la période de révolution
T et du rayon
R
de l’orbite d’une planète à trajectoire circulaire.
2)-
Exercices :
a)-
Exercice 9 page 172 : Étudier le lancer du poids.
b)-
Exercice 10 page 173 : Faire une analyse dimensionnelle.
c)-
Exercice 17 page 174 : Étude du canon à électrons.
d)-
Exercice 18 page 175 : Neptune et Galatée.
e)-
Exercice 20 page 176 : Poids et force électrostatique.
f)-
Exercice 21 page 176 : De l’optique avec des électrons.
g)-
Exercice 22 page 177 : Quelle est la masse de Jupiter.
h)-
Exercice 26 page 179 : Principe du spectromètre de masse.
|
|
|
|
