1)- Exercices : 5 page 282. 

 Bille avec vitesse horizontale.

-   Schéma :

1)- Allure de la trajectoire.

-  À l’instant initial, le vecteur vitesse  est horizontal.

2)- Distance OM.

-  Le référentiel : référentiel terrestre considéré comme galiléen car pendant cette courte durée, on peut considérer que la terre n'a pas bougé.

-  Le repère d'espaces lié au référentiel d'étude :

-  Conditions initiales :

-  Bilan des forces : la bille est soumise à son poids .

-  On peut négliger la poussée d’Archimède et les forces de frottements.

-  Deuxième loi de Newton (Théorème du centre d'inertie) :

-  

-  Coordonnées du vecteur accélération :

et

De l’équation (1), on tire

-  Par intégrations successives, on donne les équations horaires du vecteur vitesse et du vecteur position.

D’après les conditions initiales

D’après les  conditions initiales

-  Équation de la trajectoire :

-  On élimine te temps entre les équations (1) et (2).

-  

-  Lorsque la bille touche le sol,  y = 0 ceci avec le repère choisit.

-  Il faut résoudre l’équation :

-  

3)- La bille va deux fois plus loin.

-  Les autres paramètres étant inchangés, par analogie, on peut écrire :

-  

-  

-  En utilisant les relations (3) et (3’), on tire : 

-  v₁ = 2 v₀ .

2)- Exercice 20 page 285.

 Trajectoire d’une balle de volley.

-  Schéma :

1)- Trajectoire du ballon.

a)- Équation littérale de la trajectoire du ballon.

-  Le système : le ballon masse m et de centre d'inertie G.

-  Le référentiel : référentiel terrestre considéré comme galiléen car pendant cette courte durée, on peut considérer que la terre n'a pas bougé.

-  Le repère d'espaces lié au référentiel d'étude :

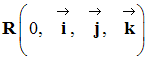
-  Conditions initiales :

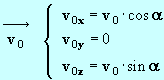-  Bilan des forces : la balle est soumise à son poids .

-  On peut négliger la poussée d’Archimède et les forces de frottements.

-  Deuxième loi de Newton (Théorème du centre d'inertie) :

-  

-  Coordonnées du vecteur accélération, du vecteur vitesse et du vecteur position.

Vecteur accélération

et

De l’équation (1),  on tire

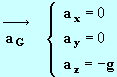Vecteur vitesse

D’après les conditions initiales

Vecteur position

D’après les conditions initiales

-  Équation de la trajectoire du ballon : on élimine le temps entre les relations (1) et (2).

- 

-  En ordonnant et simplifiant :

-  

b)- Altitude maximale atteinte par le ballon.

-  L’altitude maximale est obtenue lorsque α = 90 °. 

-  Dans ce cas, le mouvement du ballon est vertical

-  Dans ce cas, l’équation devient :

- 

-  Au sommet de la trajectoire, la vitesse du ballon s’annule.

- 

2)- étude du service.

a)- Validité du service.

-  Étude préliminaire : pour passer le filet, il faut que lorsque x = d  +  D (position du filet), z ≥ H (hauteur du filet)

-  Il faut aussi que lorsque , une solution de cette équation du second degré soit inférieure à d + 2 D.

-  Vérification :

-  

-  Le ballon passe au-dessus du filet z > H.

-  Le ballon tombe dans le terrain :

-  Il faut résoudre l’équation : – 4,5 x 10 ^{– 2} x²  +  0,58 x  +  1,80 = 0

-  Les solutions : x₁ ≈ 15,5 m et x₂ ≈ – 2,5 m, la bonne solution est x₁ ≈ 15,5 m < d + 2 D = 19 m.

-  Le service est bon, il passe au-dessus du filet et tombe dans le terrain adverse.

b)- Distance entre le filet et le point de chute du ballon :

-  d₁ = x₁ – ( d + D)

-  d₁ ≈ 15,5 – 10

-  d₁ ≈ 5,5

c)- Temps dont dispose le joueur.

-  Avant de toucher le sol, le ballon parcourt la distance x₁ ≈ 15,5 m.

-  De l’équation x = v ₀ . t . cos a (1), on tire :

-  

3)-  Exercice23 page 287.

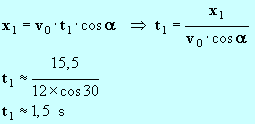
 Chute libre d’un train.

1)- Le vecteur vitesse à l’instant du lâcher.

-  À L’instant initial, l’objet possède la vitesse par rapport au sol.

-  Schéma :

2)-  Équations horaires du mouvement.

-  Le référentiel : référentiel terrestre considéré comme galiléen car pendant cette courte durée, on peut considérer que la terre n'a pas bougé.

-  Le repère d'espaces lié au référentiel d'étude :

-  Conditions initiales :

-  Deuxième loi de Newton (Théorème du centre d'inertie) :

-  

-  Coordonnées des différents vecteurs dans le repère d’étude.

-  Coordonnées des vecteurs forces :

-  La relation (1) permet de déterminer les coordonnées du vecteur accélération.

-  

-  Par intégrations successives, on donne les équations horaires du vecteur vitesse et du vecteur position.

3)- Distance OI.

-  Lorsque l’objet touche la voie ferrée, avec le repère choisi, z = 0.

-  De l’équation (2), on tire l’expression de t que l’on remplace dans l’équation (1) :

-  

4)- Exercice 26 page 288.

 étude du mouvement d’une balle de tennis.

1)-  La courbe z = f₃ (x) représente la trajectoire de la balle.

-  Le mouvement de la balle a lieu dans le plan zOx.

-  Cette courbe représente les variations de la côte z en fonction de l’abscisse x.

2)- étude des différentes courbes.

a)- Graphe x = f₁ (t).

-  Les points sont alignés.

-  La courbe est une portion de droite passant par l’origine : x = k t.

-  L’abscisse de la balle est proportionnelle au temps.

-  Le mouvement  de la projection de la balle sur l’axe Ox est rectiligne uniforme.

-  La balle parcourt des distances égales pendant des durées égales.

b)- La valeur de la composante v_x est donnée par celle du coefficient directeur de la droite x = k t.

- 

3)- Valeur de la composante v_z (0).

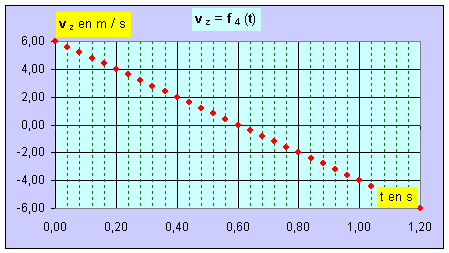
-  Il faut utiliser le graphe v_z = f₄ (t).

-  Il faut tracer la droite moyenne et l’ordonnée à l’origine permet de déterminer la valeur de la composante v_z (0) ≈ 6,0 m / s.

4)- Valeur de l’angle de tir.

-  Schéma :

-  On connaît :

-