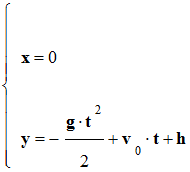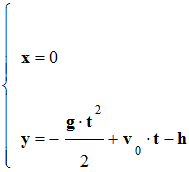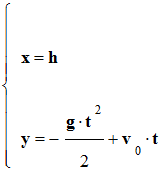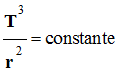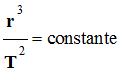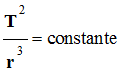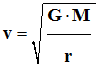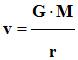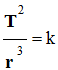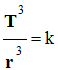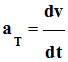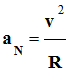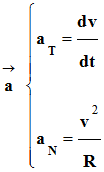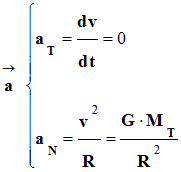QCM N° 06 Applications des lois de Mewton et Kepler. Terminale S 2012

QCM N° 06

Applications des

lois de Newton

et Kepler

QCM N° 06 Application des lois de Newton et Kepler AIDE Pour chaque question, indiquer la (ou les) bonne(s) réponse(s).
	Énoncé	A	B	C	R
1	Tigibus lance un bouton de masse m verticalement, vers le haut, à partir d’une hauteur h. La valeur de la vitesse initiale est v₀. On étudie le mouvement du bouton dans le repère contenu dans le plan de la trajectoire. L’intensité de la pesanteur est notée g. Schéma de la situation à l’instant t : Un référentiel pertinent pour étudier le mouvement du bouton est :	Le référentiel héliocentrique.	Le référentiel géocentrique.	Un référentiel terrestre.	C
2	Dans l’hypothèse d’une chute libre, le bouton est uniquement soumis :	À son poids et aux forces de frottements de l’air.	À son poids	Aux forces de frottements de l’air.	B
3	Le vecteur accélération du bouton est :	Vertical ascendant.	Vertical descendant.	Horizontal et dans le sens du mouvement.	B
4	À chaque date t, l’abscisse v_x du vecteur vitesse du bouton est :	0	v₀	– v₀	A
5	À chaque date t, l’ordonnée v_y du vecteur vitesse du bouton est :	– g . t + v₀	+ g . t + v₀	– g . t – v₀	A
6	Les équations horaires du mouvement sont :				A
7	La trajectoire du bouton est :	Parabolique.	Circulaire.	Rectiligne.	C
8	Le référentiel le plus adapté à l’étude du mouvement de la Lune autour de la Terre est :	Le référentiel héliocentrique.	Le référentiel géocentrique.	Le référentiel terrestre.	B
9	Dans l’approximation d’une trajectoire circulaire, le mouvement de la Lune dans ce référentiel est :	Rectiligne uniforme.	Circulaire uniforme.	Circulaire non uniforme.	B
10	D’après la loi des aires, le segment de droite reliant les centres de gravité de la Lune et de la Terre :	Balaie des aires égales pendant des durées égales.	A une trajectoire elliptique.	A une longueur constante.	A
11	Un satellite est en orbite autour de la Terre. Il effectue une révolution de rayon r avec une période T. La troisième loi de Kepler s’écrit :				BC
12	La valeur de l’accélération d’un point mobile en mouvement circulaire uniforme :	Est nulle.	Quadruple si la valeur de la vitesse double.	Augmente si le rayon de la trajectoire augmente.	B
13	Dans l’approximation des trajectoires circulaires, de rayon r, autour d’un astre de masse M, la valeur de la vitesse d’un satellite vérifie la relation :				A
14	Dans l’approximation des rajectoires circulaires autour d’un astre, la période T de révolution et le rayon r de la trajectoire d’un satellite vérifient la relation :				A
15	Dans la relation correcte précédente :	k dépend de la masse du satellite.	k dépend de la masse de l’astre autour duquel le satellite tourne.	k est une constante universelle.	B
16	Le mouvement de Jupiter est circulaire dans le référentiel :	Géocentrique.	Héliocentrique.	Jovicentrique.	B

Questionnaire a été réalisé avec Questy Pour s'auto-évaluer

AIDE

Phys. N° 04 La Relativité du mouvement.

- Le référentiel terrestre ou référentiel du laboratoire.

- On utilise, le plus souvent, comme repère lié au référentiel terrestre, deux axes horizontaux et un axe vertical.

- Ce référentiel est bien commode pour l’étude du mouvement des objets dans une salle de classe, pour tous les mouvements qui s’effectuent au voisinage de la terre.

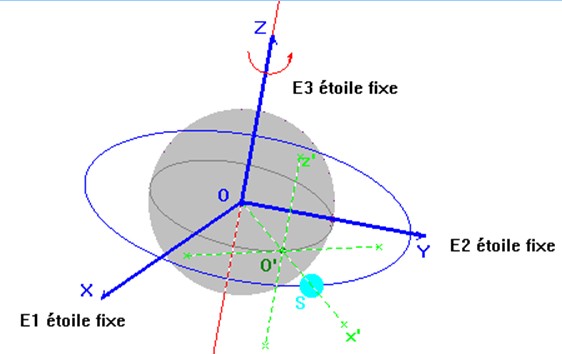
- Le référentiel géocentrique.

- L’origine du repère lié au référentiel Géocentrique est située au centre de la Terre.

- L’axe z’Oz est orienté vers une étoile lointaine : on peut choisir l’étoile polaire.

- Les axes x’Ox et y’Oy sont situés dans le plan équatorial et ils sont orientés vers des étoiles lointaines supposées fixes.

référentiel géocentrique

- Ce référentiel est commode pour l’étude des satellites de la Terre.

- Ce référentiel n’est pas entraîné dans le mouvement de rotation de la Terre.

- Dans ce référentiel, la Terre est animée d’un mouvement de rotation uniforme de l’ouest vers l’est, autour de l’axe des pôles.

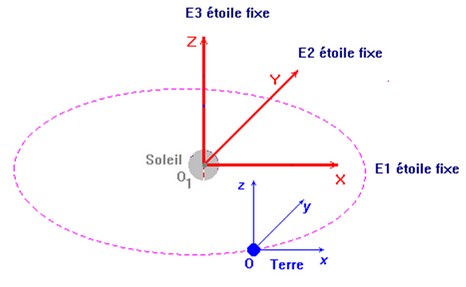
- Le référentiel héliocentrique ou de Copernic.

- L’origine du repère lié au référentiel Héliocentrique est située au centre du Soleil.

- Les axes z’Oz, x’Ox et y’Oy sont orthogonaux et ils sont orientés vers des étoiles lointaines supposées fixes.

- Ce référentiel est commode pour l’étude des satellites du Soleil. Dans ce référentiel, la Terre décrit une orbite elliptique autour du Soleil en une année.

référentiel héliocentrique

- Chute libre :

- On appelle chute libre le mouvement d'un objet soumis uniquement à son poids .

- Conséquence de l'application de la deuxième loi de Newton :

- Application de la deuxième loi de Newton :

- Dans un référentiel galiléen, si un système assimilé à un point matériel est soumis à une ou plusieurs forces extérieures,

alors la somme vectorielle de ces forces est égale à la dérivée par rapport au temps de son vecteur quantité de mouvement :

- On écrit :

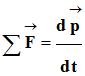
- deuxième loi de Newton

- Comme la masse m de la balle ne varie pas au cours du temps, on peut en déduire la relation suivante :

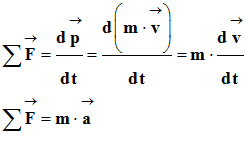
- deuxième loi de Newton

- D’où :

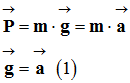
- relation

- Vitesse initiale :

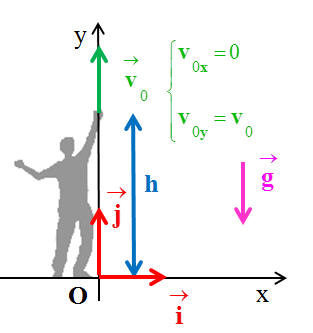
chute libre

- On utilise la relation :

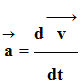
- vecteur accélération

- Le vecteur accélération est la dérivée par rapport au temps du vecteur vitesse .

- La détermination du vecteur vitesse nécessite de rechercher la primitive par rapport au temps de chaque coordonnée du vecteur accélération en tenant compte des conditions initiales.

- On cherche les primitives des équations précédentes.

- Il apparaît des constantes qui sont liées aux conditions initiales.

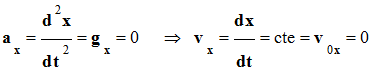
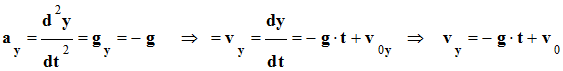
équation horaire

- Loi des aires.

- Le segment de droite qui relie le centre du Soleil au centre de la planète balaie des aires égales pendant des durées égales.

- Il résulte de ceci que la planète se déplace plus vite lorsqu’elle se rapproche du Soleil.

- En toute rigueur, le mouvement d’une planète n’est pas uniforme.

Vecteur accélération :

Vecteur accélération		Le vecteur accélération tangentielle	Le vecteur accélération normale

	Direction	Tangent à la trajectoire au point considéré	Centripète
	Sens	Orienté dans le sens du mouvement	Orienté vers le centre du cercle
	Valeur	C’est la dérivée par rapport au temps de la valeur de la vitesse v

Vecteur

accélération

Relation

vecteur accélération : coordonnées

- En conséquence : 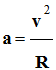a = v² / R

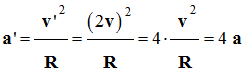
- Si v’ = 2 v, relation

- D’autre part, si R↑, a↓.

- De l’accélération à la vitesse :

- v = cte

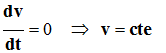
- Le satellite est animé d’un mouvement circulaire uniforme.

- D’autre part :

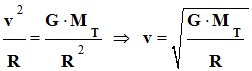
- relation

- La valeur de la vitesse du satellite est indépendante de sa masse.

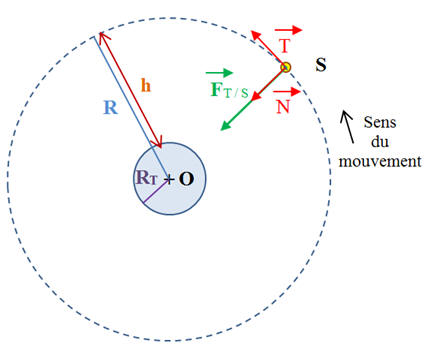
mouvement circulaire

- Loi des périodes.

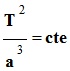- Pour toutes les planètes, le rapport entre le cube du demi-grand axe a de la trajectoire et le carré de la période T de révolution est la même : Loi des périodes .

- Cette constante ne dépend pas de la masse de la planète.

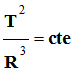- Si la trajectoire est un cercle de rayon R, on peut écrire que : Loi des périodes .

- Cette constante peut être calculée.

- Exemple :

- Dans le cas du système solaire, on peut donner l’expression de la période de révolution d’une planète du système solaire :

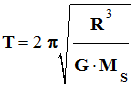
- période de rotation

- En élevant cette expression au carré et en ordonnant, on peut écrire :

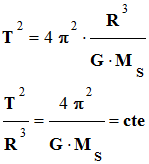
- Loi des périodes

- Référentiel jovicentrique :

- Référentiel galiléen lié au centre de Jupiter

- C'est un référentiel dont l'origine est le centre de Jupiter et dont les axes sont parallèles à ceux du référentiel héliocentrique.

- On utilise le référentiel jovicentrique pour l’étude du mouvement des satellites de Jupiter.