|
Phys.
N° 07 :
et des planètes
|
|
|
|
|
I- Mouvement
des Satellites de la Terre. |
|
II- Satellite
Artificiel à trajectoire circulaire.
On suppose que la Terre a
une distribution
de masse à symétrie sphérique de centre
O. |
|
3)- Mouvement de la planète Mars :
exercice 11 page 119.
4)- Détermination de la masse d’une Planète :
exercice 12 page 119. |
I-
Mouvement des Satellites de la Terre.
1)-
Le
référentiel
Géocentrique.
-
Le référentiel
terrestre ou référentiel du laboratoire.
- On utilise, le plus souvent, comme repère lié au référentiel terrestre, deux axes horizontaux et un axe vertical.
- Ce référentiel est bien commode pour l’étude du mouvement
des objets dans une salle de classe, pour tous les mouvements qui s’effectuent
au voisinage de la terre.
- Si l’expérience est suffisamment courte, on peut considérer que ce référentiel est Galiléen avec une bonne approximation
- (Précision de l’ordre de
10 –2 à 10
–3).
-
Le référentiel
géocentrique.
- L’origine du repère lié au référentiel Géocentrique est située au centre de la Terre.
- L’axe z’Oz est orienté vers une étoile lointaine : on peut choisir l’étoile polaire.
- Les axes
x’Ox et y’Oy sont situés
dans le plan équatorial et ils sont orientés vers des étoiles lointaines
supposées fixes.
- Ce référentiel est commode pour l’étude des satellites de la Terre.
- Ce référentiel n’est pas entraîné dans le mouvement de rotation de la Terre.
- Dans ce référentiel, la
Terre est animée d’un mouvement de rotation uniforme de l’ouest vers l’est,
autour de l’axe des pôles.
-
on
peut considérer que ce référentiel est Galiléen avec une bonne approximation
(Précision de l’ordre de 10 –3 à 10 –4).
-
Schéma :

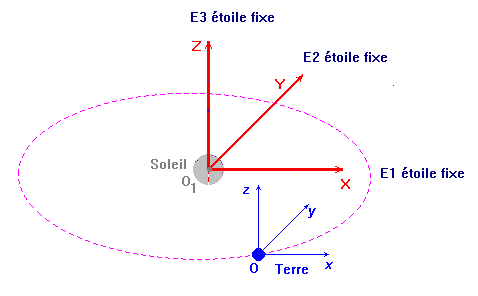
2)- Le référentiel héliocentrique ou de Copernic.
- L’origine du repère lié au référentiel Héliocentrique est située au centre du Soleil.
- Les
axes z’Oz, x’Ox et y’Oy sont orthogonaux et ils sont orientés vers des étoiles
lointaines supposées fixes.
- Ce référentiel est commode pour l’étude des satellites du Soleil.
- Dans ce référentiel, la Terre décrit une orbite elliptique autour du Soleil en une année.
-
on peut considérer que ce
référentiel est Galiléen avec une très bonne approximation
(Précision de l’ordre de 10
–10).
-
Schéma :
II-
Satellite Artificiel à trajectoire circulaire.
|
a)-
Donner l’expression de
l’intensité du champ de gravitation
g créé
par la Terre à une altitude
h en fonction de
G, RT et
h. Faire un
schéma.
b)-
Donner l’expression
vectorielle de la force
c)-
Donner l’expression
littérale de MT en fonction de
g0,
G
et RT
et calculer sa valeur.
- On donne : G = 6,67 x 10
–11 S.I
;
RT = 6400 km ; g0 = 9,80 m / s2
(au
niveau du sol). ► CAVENDISH : (1798) Il mesure la constante G en utilisant un dispositif analogue à la balance de torsion qui avait permis à COULOMB d’établir en 1785 la loi de l’électrostatique.
La connaissance de
G permis la mesure de la masse des
autres Astres. (Lois de KEPLER). |
|
a)-
expression
de l’intensité du champ de gravitation :
-
expression
vectorielle :
-
-
En
conséquence :
-
b)-
Expression
vectorielle de la force
-
c)-
Expression
littérale de MT en fonction de g0,
G et RT
et valeur.
-
|
|
Il décrit dans le référentiel géocentrique
une trajectoire circulaire de centre O.
a)-
Donner les
caractéristiques du vecteur accélération
b)-
Montrer que le mouvement
du Satellite est uniforme. c)- Exprimer la valeur de la vitesse v du Satellite en fonction de MT, G, RT et h.
(Le mouvement étant circulaire, il faut
travailler dans le repère de FRENET).
-
Dans quel repère
cette vitesse est-elle mesurée ?
-
Calculer
v
pour h = 300 km et
h = 30000 km. Conclusion.
d)-
Exprimer la valeur de la
période T du Satellite en fonction
de
MT,
G,
RT et
h puis en fonction de
RT et
h
et g0.
-
Calculer
T
pour h = 300 km et
h = 30000 km. Conclusion.
-
Donner
l’expression littérale du rapport :
-
Le Satellite
EXPLORER gravite à une altitude h
= 180 km. Calculer sa période
T
de révolution. |
|
a)- Caractéristiques
du vecteur accélération.
-
Système :
Satellite S (m, G)
-
Référentiel géocentrique :
-
Schéma :
- Bilan des forces :
-
-
On
néglige les forces de gravitation exercées par les autres planètes et le
Soleil.
-
Le théorème du centre
d’inertie : Dans un référentiel Galiléen, la somme des vecteurs forces extérieures appliquées à un solide
est égale au produit de la masse du solide par le vecteur
accélération de son centre d’inertie.
On écrit :
- Le vecteur accélération a même direction,
- même sens et même valeur que le
vecteur champ de gravitation
-
L’accélération du centre d’inertie du Satellite est égale au
champ
gravitationnel.
-
Elle est
dite centripète (orientée vers le centre de la Terre.
-
Le
Satellite est soumis à une force centrale
- Le plan de la trajectoire du Satellite contient
-
le centre O de la Terre.
b)- Le mouvement du Satellite est
uniforme : - Le mouvement étant circulaire, il faut travailler dans
- le repère de FRENET.
-
-
schéma :
-
Coordonnées de chaque vecteur dans le repère de FRENET :
-
-
De
l’équation (1), on tire :
-
Le
mouvement du Satellite a lieu dans le plan xOy.
-
De plus
comme :
- le
mouvement est uniforme. - Comme le mouvement du Satellite est circulaire,
-
il est circulaire uniforme.
c)-
Expression de la
vitesse du Satellite.
-
Cette
vitesse est mesurée dans le référentiel Géocentrique, elle est
indépendante de la masse du Satellite.
-
Calcul de
la valeur de la vitesse :
-
-
-
Quand
l’altitude h augmente, la vitesse v
du Satellite diminue.
d)-
Période du
Satellite :
-
La
période du Satellite est la durée nécessaire pour effectuer un tour.
-
-
expression
de T en fonction de g0 et h.
-
-
Valeur de
T pour les deux altitudes :
-
-
-
Quand
l’altitude h augmente, la période T augmente aussi.
-
Expression littérale du rapport :
-
On part
de l’expression suivante que l’on élève au carré
-
-
Le
rapport est constant et indépendant de la masse du Satellite. Ce
résultat constitue la Troisième loi de Kepler.
e)-
Période T du Satellite
EXPLORER.
-
|
5)- Satellite Géostationnaire.
|
►Un Satellite Géostationnaire est un Satellite qui reste toujours à la verticale d’un même point P de la Terre. - Le plan de l’orbite dans
le référentiel géocentrique est le plan équatorial.
-
Quelle est la
période de révolution d’un tel Satellite ?
-
En déduire
l’altitude h d’un Satellite géostationnaire. |
|
►
Solution :
-
Période
de révolution d’un Satellite Géostationnaire : - C’est la durée pour effectuer un tour dans le référentiel géocentrique :
- c’est la
durée d’un jour sidéral
-
1 j =
86164 s = 23 h 56 min 4 s - altitude de révolution d’un Satellite Géostationnaire :
|
- Les neuf Planètes gravitent approximativement dans le même plan autour d’une étoile centrale : Le Soleil.
- Ce plan qui contient le centre du Soleil est appelé : Plan de
l’écliptique.
- Le système Solaire comprend : le Soleil et les planètes :
- Mercure, Vénus, Terre, Mars, Jupiter, Saturne, Uranus, Neptune et Pluton.
- Les trajectoires des planètes sont des ellipses très voisines de cercles
- (sauf pour Pluton qui joue un rôle un peu
particulier).
-
Dans le
référentiel Héliocentrique, le mouvement du centre d’une planète autour du
Soleil est quasiment circulaire.
-
Le centre de
chaque trajectoire circulaire coïncide presque avec le centre du Soleil.
|
-
Première loi de
Kepler : Dans le référentiel Héliocentrique, les planètes
décrivent des ellipses
d’un le Soleil S est un des foyers. - Deuxième loi de KEPLER : En des temps égaux, le rayon-vecteur SP balaie des aires égales
- (S désigne le centre du Soleil et
P le centre de la planète
considérée).
- Troisième loi de KEPLER : Pour toutes les planètes, le rapport entre le cube du demi-grand axe a de la trajectoire et le carré de la période T de révolution est la même :
-
Cette constante
ne dépend pas de la masse de la planète. En considérant que la
trajectoire est
circulaire, on peut écrire que :
|
3)-
Mouvement de la planète Mars :
exercice 11 page 119.
|
a)-
Définir le référentiel
Héliocentrique. b)- Exprimer le champ de gravitation dû au Soleil au centre de Mars. Préciser l’hypothèse envisagée pour
exprimer le champ de gravitation.
c)-
Dans le référentiel
Héliocentrique donner l’expression de l’accélération du centre d’inertie de Mars
en fonction de r,
MS et
G.
d)-
En déduire l’expression
littérale la période T de révolution de Mars. Calculer la valeur de cette
période. - On donne : Rayon de la trajectoire de Mars r = 2,2794 × 108 km ; masse du Soleil MS = 1,98 × 1030 kg et la constante de
gravitation Universelle G
= 6,67
× 10 –11 S.I. |
|
-
On
considère le Soleil comme un corps à répartition sphérique de masse.
-
-
Accélération du centre d’inertie de Mars dans le référentiel
Héliocentrique :
-
Système :
Satellite S (m, G)
-
Référentiel Héliocentrique :
-
Schéma :
-
- Bilan
des forces :
-
- Le
théorème du centre d’inertie : - Dans un référentiel Galiléen, la somme des vecteurs forces extérieures appliquées à un solide
est égale au produit de la masse du solide par le vecteur
accélération de son centre d’inertie.
-
On écrit :
-
-
Le
vecteur accélération a même direction, même sens et même valeur que le
vecteur champ de gravitation
-
L’accélération du centre d’inertie de Mars est égale au champ
gravitationnel.
-
Elle est
dite centripète (orientée vers le centre du Soleil).
-
Valeur de
l’accélération :
-
-
Période
de révolution de Mars.
-
On peut
déterminer l’expression de la vitesse de Mars dans le référentiel
Héliocentrique :
-
-
Et en
déduire l’expression de la période de révolution T :
-
-
Valeur de
la période T :
-
|
4)-
Détermination de la masse d’une Planète :
exercice 12 page 119.
|
a)- Lorsqu’un Satellite est animé d’un mouvement circulaire, autour d’une planète de masse M, le rayon r de son orbite
et la période
T de son mouvement vérifient
la troisième loi de Kepler :
-
- Les Satellites géostationnaires de la Terre ont une orbite circulaire de rayon rG = 42164 km et une période TG = 86164 s.
- Calculer la masse MT
de la Terre.
-
Mars a deux
Satellites naturels, Phobos et Deimos. - Phobos gravite à la distance rp = 9380 km du centre de Mars avec une période Tp = 7 h 39 min.
-
Deimos a une trajectoire quasi circulaire
de rayon
rD = 23460 km et une période de révolution
TD
= 30 h 18 min.
b)-
Calculer la masse
MM
de la planète Mars à partir des caractéristiques du
mouvement de Phobos et de
Deimos.
-
Comparer les
valeurs obtenues. c)- Au cours de la mission APOLLO XVII en 1972, le module de commande en orbite autour de la Lune à une distance de 2040 km du centre de celle-ci, avait une période de 8240 s dans le référentiel Sélénocentrique. Calculer la masse de la Lune. |
|
Solution :
d)-
Masse de la
Terre :
-
e)-
Masse de la
planète Mars :
-
en
utilisant les caractéristiques de Phobos.
-
-
En
utilisant les caractéristiques de Deimos.
-
- Comparaison des valeurs :
-
-
Incertitude relative :
f)-
Masse de la
Lune :
-
|
|
|
|
|