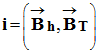|
Champs et forces. Cours. |
|
|
|
|
|
|
Exercices : énoncé avec correction a)- Exercice 7 page 213. Cartographier un champ scalaire. b)- Exercice 9 page 213. Exploiter des lignes de champ vectoriel. c)- Exercice 11 page 213. Lire une carte de vitesse des vents. d)- Exercice 12 page 213. Identifier les pôles magnétiques. e)- Exercice 18 page 215. La Terre a rendez-vous avec la Lune. f)- Exercice 20 page 215. Point d’équigravité. g)- Exercice 24 page 217. Le temps est à l’orage. h)- Exercice 25 page 217. Champ géomagnétique. |
I- Notion de champ.
1)- Définition.
► Quelques exemples :
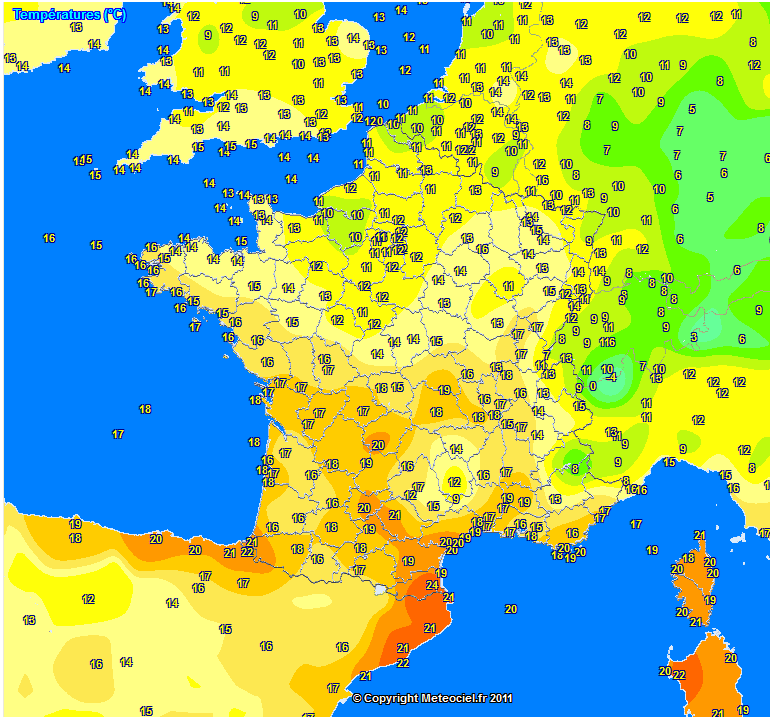
- Cartes de température : Sources site https://www.meteociel.fr/
- Carte de la pression (tracé des isobares) : Sources site https://www.meteociel.fr/
- Carte de la vitesse du vent : Sources site https://www.meteociel.fr/
► Observations :
- Remarques principales :
 Que représentent les lignes tracées sur la carte
relative à la pression ?
Que représentent les lignes tracées sur la carte
relative à la pression ?
 Que représentent les différentes zones colorées de
la carte relative aux températures ?
Que représentent les différentes zones colorées de
la carte relative aux températures ?
 Quelles sont différentes caractéristiques du vent
en un point donné ?
Quelles sont différentes caractéristiques du vent
en un point donné ?
 Sachant que la température est une grandeur
scalaire et la vitesse du vent une grandeur vectorielle,
indiquer les différences entre ces deux types de grandeur ?
Sachant que la température est une grandeur
scalaire et la vitesse du vent une grandeur vectorielle,
indiquer les différences entre ces deux types de grandeur ?
 Qu’est-ce qu’une grandeur scalaire ? Une grandeur
vectorielle ?
Qu’est-ce qu’une grandeur scalaire ? Une grandeur
vectorielle ?
 Proposer une définition de la notion de champ à
partir de ces exemples ?
Proposer une définition de la notion de champ à
partir de ces exemples ?
► Carte relative à la pression :
- Les lignes tracées représentent les lignes isobares, lieux où la pression est la même (pression au niveau de la mer en hPa)
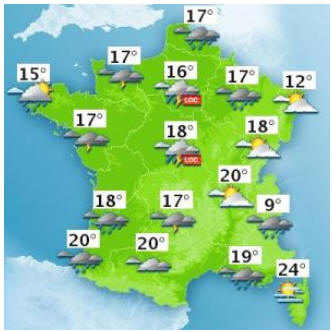
► Carte relative à la température :
- Les différentes zones colorées mettent en valeur les zones où la température est la même.
- Pour le vent, on indique grâce à la présence d’un segment fléché, la direction et le sens du vent. La couleur indique la valeur du vent.
- Les caractéristiques du vent, en un point donné, sont :
- La direction,
- Le sens,
- La valeur associée à une unité
- Pour la température ou la pression, il suffit de donner la valeur associée à une unité.
► Grandeur scalaire :
- Une grandeur scalaire (en physique) est caractérisée par un nombre suivie d’une unité.
- La connaissance du nombre et de l’unité qui lui est associée est suffisante pour connaître la grandeur scalaire.
- Exemple la température à Marseille est θ = 18 ° C et la pression p = 1016 hPa.
► Grandeur vectorielle :
- Une grandeur vectorielle (en physique) est caractérisée par :
- Son origine
- Sa direction et son sens,
- Sa valeur associée à une unité
- En physique, en représente une grandeur vectorielle par un segment fléché :
- Origine : position considéré, point d’application, …
- Direction et sens
- Valeur associée à une unité
- Une échelle pour affecter une longueur au vecteur.
- La longueur du représentant est proportionnelle à la valeur.
-
Exemple : le vecteur force
 , le vecteur vitesse
, le vecteur vitesse
 , …
, …
-
Dans le cas de la carte du vent, on peut utiliser comme
grandeur vectorielle, le vecteur vitesse que l’on note 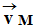 : vitesse du vent au point M de l’espace considéré.
: vitesse du vent au point M de l’espace considéré.
|
|
Origine : |
Point M |
|
La direction ; |
Droite (AB) |
|
|
Le sens |
de B vers A. |
|
|
L’intensité ou valeur |
vM = 21 km / h |
|
|
Longueur du représentant
Échelle :
1 cm ↔ 10 km / h |
ℓvM = 2,1 cm |
- Représentation :

- La carte des températures représente un champ scalaire alors que la carte des vitesses du vent représente un champ vectoriel.
► Définitions :
- Un champ scalaire est défini par une valeur associée à une unité en chaque point de l’espace considéré.
- Un champ vectoriel est défini par un vecteur (direction, sens, valeur et unité) en chaque point.
![]() De façon générale, un champ est une grandeur
physique (scalaire ou vectorielle) associée à chaque point de
l’espace considéré.
De façon générale, un champ est une grandeur
physique (scalaire ou vectorielle) associée à chaque point de
l’espace considéré.
2)- Champ scalaire et champ vectoriel.
a)- Cartographie d’un champ.
![]() Pour cartographier un champ, on détermine les
caractéristiques de ce champ en certains points de l’espace et
on en donne une représentation.
Pour cartographier un champ, on détermine les
caractéristiques de ce champ en certains points de l’espace et
on en donne une représentation.
- Le nombre de points choisis est lié à la précision du champ que l’on veut représenter.
- Dans le cas d’une cartographie des températures, on peut donner la température d’une région, ou donner la température par ville.
- Cartographie des températures : chaque station météo donne la température du lieu sous abri.

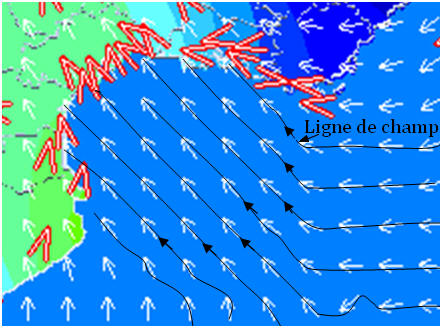
b)- Ligne de champ vectoriel.
- Dans le cas d’un champ vectoriel, on peut définir les lignes de champ.
![]() Une ligne de champ vectoriel est une ligne
tangente en chacun de ses points au vecteur champ.
Une ligne de champ vectoriel est une ligne
tangente en chacun de ses points au vecteur champ.
Elle est orientée par une flèche dans le même sens que celui du champ.
- Exemple : On peut tracer les lignes de champ de la carte des vents :
3)- Champ uniforme.
![]() Un champ uniforme est un champ dont les
caractéristiques ne dépendent pas du point de l’espace
considéré.
Un champ uniforme est un champ dont les
caractéristiques ne dépendent pas du point de l’espace
considéré.
- Cas d’un champ vectoriel :
- On peut représenter ce champ par un vecteur qui indique, la direction, le sens et la valeur du champ dans tout l’espace considéré.
-
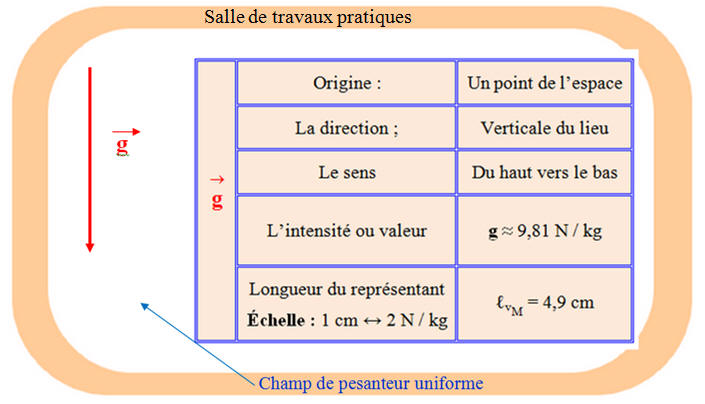
Exemple : Ainsi, si on s’intéresse au champ de pesanteur
dans une salle de travaux pratiques, on peut représenter ce
champ de pesanteur par le vecteur
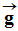 .
.
II- Champ magnétique.
Pour aller plus loin : Cours : Champ magnétique
1)- Détection et effets d’un champ magnétique.
a)- L’aiguille aimantée :
 Expérience : on place une aiguille aimantée au
voisinage d’un aimant droit.
Expérience : on place une aiguille aimantée au
voisinage d’un aimant droit.
- On remarque qu’elle s’oriente différemment selon la position du point.
- L’aiguille aimantée subit une action mécanique à distance de la part de l’aimant droit.
- Par convention, on désigne par pôle Nord l’extrémité d’une aiguille aimantée qui désigne le Nord géographique et par pôle Sud l’autre extrémité.

- Interaction entre aimants : 2 pôles de même nom se repoussent et 2 pôles de nom différent s’attirent.
► Conclusion :
![]() Une aiguille aimantée permet de mettre en évidence
l’existence d’un champ magnétique dans une région de l’espace.
Une aiguille aimantée permet de mettre en évidence
l’existence d’un champ magnétique dans une région de l’espace.
b)- Analogie courant – aimant.
- Expérience d’Oersted : un conducteur parcouru par un courant engendre une interaction électromagnétique avec un aimant.
- Il crée dans tout l’espace environnant un champ magnétique.
- Faces d’une bobine :
- Une bobine est constituée d’un enroulement de fil conducteur, recouvert d’un vernis isolant, sur un cylindre de rayon r.
- On désigne par L la longueur de l’enroulement et par r le rayon d’une spire :
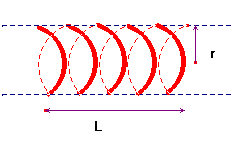
- Si L est petit devant r, la bobine est plate
- Si L est voisin de r la bobine est appelée : solénoïde
- Si L est plus grand que 10 r, le solénoïde est dit infini.
- Une bobine parcourue par un courant se comporte comme un aimant, elle possède une face Nord et une face Sud.
- Règles pour déterminer les faces Nord et Sud d’une bobine :
- Vue de face :
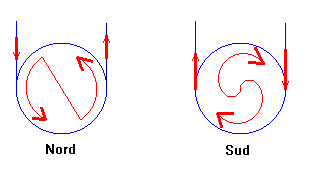
- Vue de profil : règle de la main droite
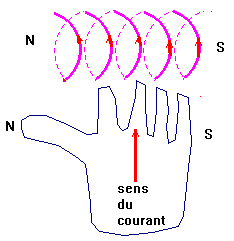
c)- Conclusion :
- Un aimant ou un conducteur parcouru par un courant agit à distance sur tout autre aimant.
- Il modifie les propriétés de l’espace qui l’environne.
- On dit qu’il produit un champ magnétique.
- Pour détecter ce champ magnétique, on utilise le plus souvent une aiguille aimantée.
- Cette aiguille détectrice subit un couple de forces qui l’oriente.
- Elle donne l’orientation du champ magnétique de la position qu’elle occupe.
d)- Pour aller plus loin :
- Un aimant ou une bobine parcourue par un courant peut agir sur une particule chargée en mouvement.
- Elle peut modifier la direction du mouvement d’une particule chargée.
- Exemple : déviation d’un faisceau d’électrons par un champ magnétique créé par les bobines d’Helmholtz.
- La trajectoire rectiligne peut devenir circulaire sous l’effet d’un champ magnétique.
- Figure 1 :
Animation CabriJava
Cours : Mouvement d'une particule chargée dans un champ magnétique uniforme
2)- Le vecteur champ magnétique
a)- Représentation du champ magnétique.
- L’orientation prise par l’aiguille aimantée dépend du point P de l’espace où elle est placée.
- Si on déplace l’aiguille dans la région de l’espace proche de l’aimant, elle change d’orientation.
- Le champ magnétique que détecte l’aiguille aimantée a les propriétés d’un vecteur.
- Le champ magnétique est un champ vectoriel.
► Représentation du champ magnétique :
- En un point P de l’espace, le champ magnétique est représenté par un vecteur :
|
|
Le point d’application P |
|
La direction : celle de l’aiguille aimantée placée en ce point |
|
|
Le sens dirigé du pôle Sud vers le pôle Nord de l’aiguille détectrice ou du pôle Nord vers le pôle Sud de la source de champ. |
|
|
Valeur B en tesla (T) |
- Pour mesurer un champ magnétique, on utilise un teslamètre à sonde de Hall.
- Cette sonde délivre une tension proportionnelle à la valeur du champ magnétique.
- Cette tension est amplifiée par un système électronique.
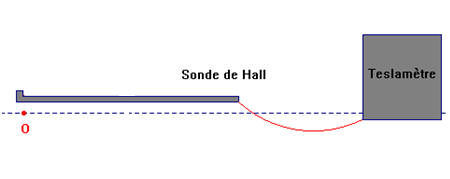
- Dans le S.I., l’unité de champ magnétique est le tesla, symbole T.
b)- Champ magnétique et ligne de champ.
- Pour visualiser le spectre magnétique d’un aimant, on utilise de la limaille de fer.
- En présence de l’aimant, les grains de limaille de fer se comportent comme autant d’aiguilles aimantées qui s’orientent sous l’action du champ magnétique.
- Elles s’orientent et dessinent des lignes, appelées lignes de champ.
- L’ensemble des lignes de champ donne le spectre magnétique.
- Les lignes de champ ainsi formées sont appelées lignes de champ magnétique.
-
Le vecteur champ magnétique
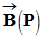 est tangent à la
ligne de champ qui passe par le point P considéré.
est tangent à la
ligne de champ qui passe par le point P considéré.
- La ligne de champ est orientée dans le sens du champ magnétique du pôle Nord vers le pôle Sud N → S de la source de champ.
3)- Le champ magnétique terrestre.
a)- Caractéristique du champ magnétique terrestre.
- Le champ magnétique terrestre trouve son origine dans les mouvements de matière se déroulant à l’intérieur du globe terrestre
(courants électriques provoqués par les courants de convection dans le noyau ; fluide conducteur, principalement du fer en fusion).
-
En un point déterminé de la surface de la terre, le
vecteur champ magnétique
terrestre
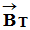 a les
caractéristiques suivantes :
a les
caractéristiques suivantes :
- Il est contenu dans un plan vertical, passant par les pôles magnétiques terrestres, appelé : Plan méridien magnétique.
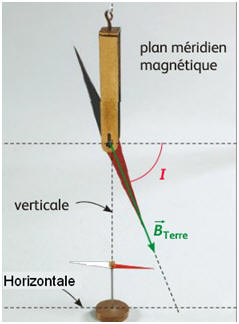
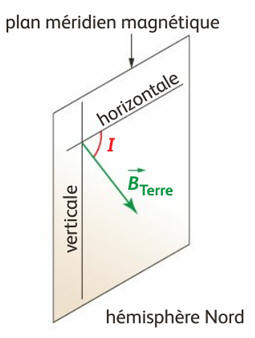
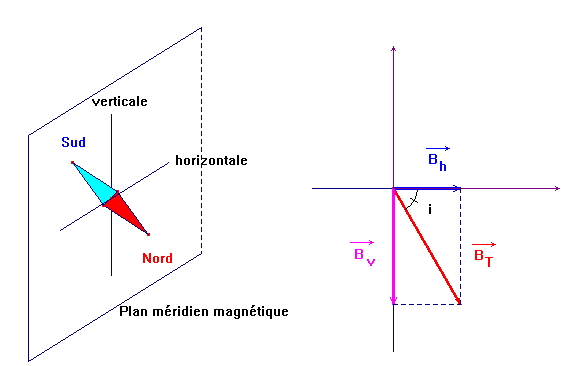
-
Son pôle Nord s’incline vers le sol.
-
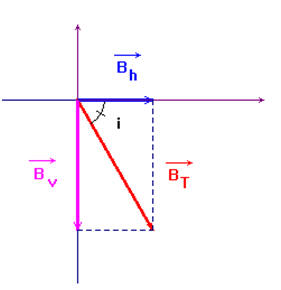
Sa direction fait avec l’horizontale un angle i
appelé inclinaison (en France, i ≈ 60 °)
-
Ce champ 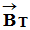 peut être
décomposé en :
peut être
décomposé en :
|
Une composante horizontale
|
|
|
Et une composante verticale
|
|
-
Remarque : l’aiguille aimantée d’une boussole disposée
horizontalement n’est sensible qu’à la composante horizontale
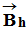 du champ magnétique
du champ magnétique
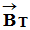 .
.
- La mesure de la valeur du champ magnétique BT est difficile à faire avec une sonde de Hall, car la valeur est faible.
- On peut mesurer la valeur de Bh grâce à la boussole des tangentes.
► application : Déterminer, en un point O de la surface de la terre, les valeurs de Bv et BT, sachant que Bh ≈ 2,0 x 10 – 5 T,
- Schéma :
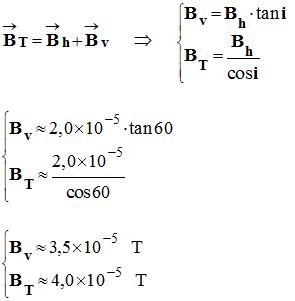
-
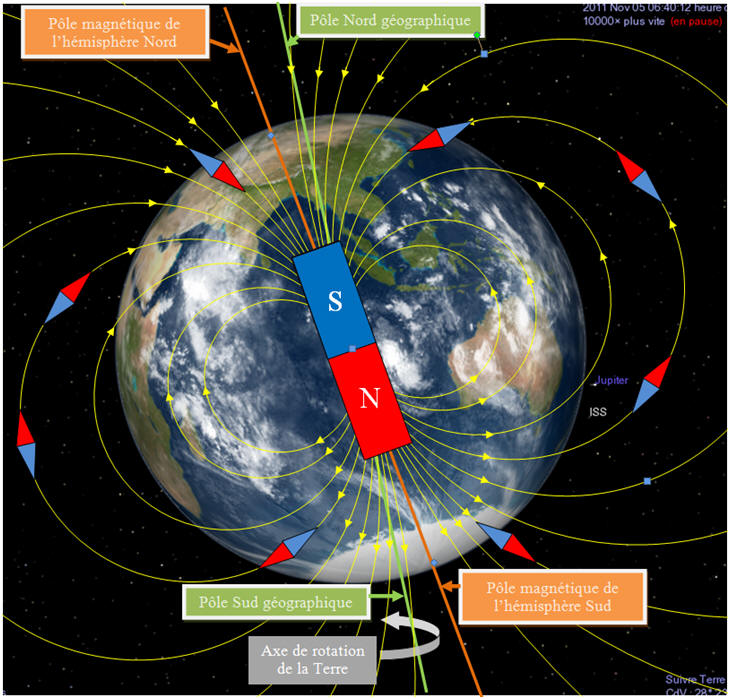
b)- Modélisation du champ magnétique terrestre.
- Le champ magnétique terrestre peut être modélisé par le champ créé par un aimant droit placé à l’intérieur du globe terrestre.
- Actuellement, le pôle magnétique de l’hémisphère Nord, au sens géographique, est un pôle magnétique Sud et le pôle magnétique de l’hémisphère Sud, au sens géographique, est un pôle magnétique Nord.
- Les boussoles s’orientent le long des lignes de champ magnétique terrestre.
- Le pôle Nord de l’aiguille aimantée de la boussole est attiré par le pôle terrestre magnétique Sud.
- Le pôle de la Terre appelé Nord magnétique est distant d’environ 1000 km du Nord géographique.
- Il est situé près du pôle Sud du modèle de l’aimant droit.
- Ce pôle doit son nom à sa proximité avec le pôle Nord géographique.
4)- Champ magnétique uniforme : L’aimant en U et le solénoïde.
a)- L’aimant en U :
- Spectre magnétique de l’aimant en U.
- Pour visualiser le spectre magnétique de l’aimant en U, on utilise de la limaille de fer.
- En présence de l’aimant, les grains de limaille de fer se comportent comme autant d’aiguilles aimantées qui s’orientent sous l’action du champ magnétique.
- Elles s’orientent et dessinent des lignes, appelées lignes de champ.
- L’ensemble des lignes de champ donne le spectre magnétique.
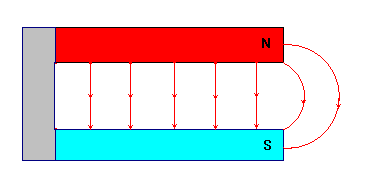
- On remarque qu’à l’intérieur de l’aimant en U, les lignes de champ sont parallèles.
- Ceci est caractéristique d’un champ uniforme.
- Le champ magnétique est uniforme dans l’entrefer d’un aimant en U.
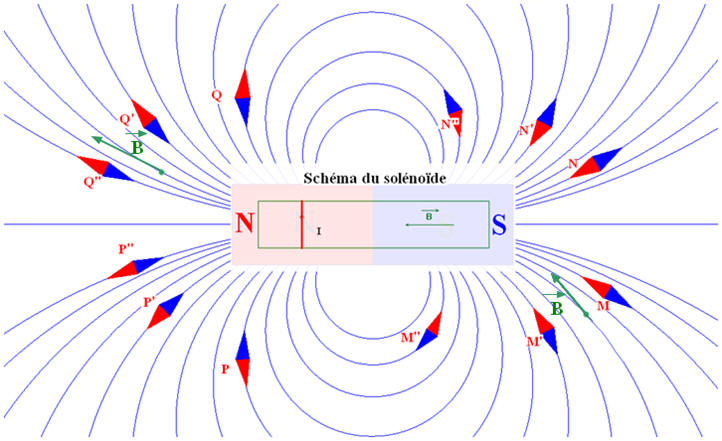
b)- Le solénoïde :
- On étudie le champ magnétique créé par un solénoïde parcouru par un courant continu, d'intensité I = 3,0 A.
- On mesure la valeur de ce champ magnétique B en différents points de l'axe x'Ox du solénoïde.
- Schéma du montage :
- Le champ magnétique à l’intérieur d’un solénoïde est pratiquement uniforme.
- Les lignes de champ à l’intérieur du solénoïde sont des droites parallèles.
- Représentation simplifiée :
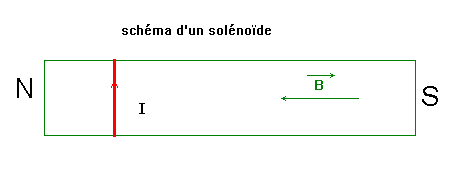
- Comparaison avec un aimant droit :
c)- Bobine de Helmholtz.
- Ce sont deux bobines plates, coaxiales, séparées par la distance ℓ et parcourues par le courant I de même intensité et de même sens.
- Si ℓ= r, le champ magnétique est pratiquement uniforme entre les bobines.
- Schéma :
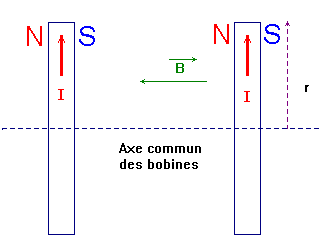
-
Caractéristiques de
 .
.
|
|
Point d’application : le champ est uniforme |
|
Direction parallèle à l’axe du solénoïde |
|
|
Sens : il sort par le pôle Nord (règle de la main droite) |
|
|
Valeur :
|
III- Champ électrique.
1)- Détection d’un champ électrique.
- Pour détecter un champ électrostatique, on utilise un pendule électrostatique électrisée.
- Placé au voisinage d’un corps portant une charge Q, le pendule s’oriente.
- Son orientation est liée à la position occupée par le pendule électrostatique électrisée.
- La charge électrique Q crée un champ électrique dans tout l’espace environnant.
- Ce champ est mis en évidence grâce à l’interaction électrostatique qui existe entre la charge électrique Q et le pendule électrostatique électrisée qui porte la charge q.
- La méthode n’est pas très précise. La charge Q doit être importante.
- Il faut utiliser la machine de Wimshurst pour créer un champ suffisamment important.

2)- Le vecteur champ électrique
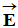 .
.
- Considérons au point O de l’espace la charge Q > 0 et au point P de l’espace la charge q > 0.
- Schéma :
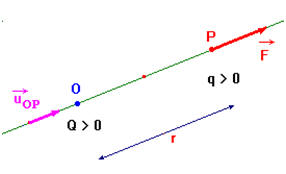
- Expression vectorielle de la force :
-

- Valeur de la force :
-


- On peut considérer que la charge Q placée au point O de l’espace, crée un champ électrique au point P :
-
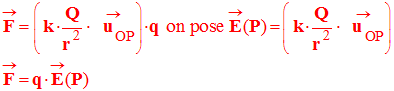
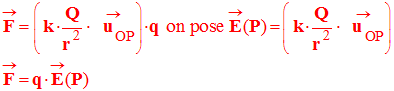
- étude de l’expression suivante : vecteur champ électrique.
-
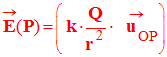
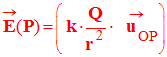
- Ce champ dépend de la charge Q, de la position du point P par rapport au point O.
- Il ne dépend pas de la charge q.
-
 :
vecteur
unitaire : direction droite (OP) et sens de O vers
P.
:
vecteur
unitaire : direction droite (OP) et sens de O vers
P.
- k : Constante
-
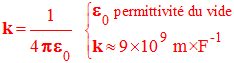
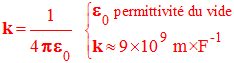
- Q : charge (source de champ) : unité : le coulomb C.
- r : distance séparant les deux charges électriques en mètre m.
-
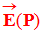 : Vecteur champ
électrique au point P
: Vecteur champ
électrique au point P
-
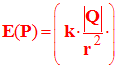 :
Valeur du champ électrique au point P unité : V /
m.
:
Valeur du champ électrique au point P unité : V /
m.
-
en
conséquence : toute charge électrique ponctuelle q placée
en un point P où règne le champ électrique
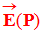 est soumise à une
force :
est soumise à une
force :
-
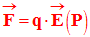
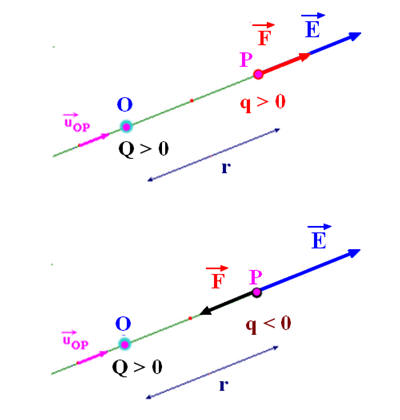
- Influence du signe de la charge q :
- La charge q a une influence sur le sens de la force électrique qu’elle subit mais n'a pas d'influence sur celui du champ électrique qu’elle subit.
3)- Champ électrique et lignes de champ.
-
On appelle ligne de champ, une courbe de l’espace à
laquelle le vecteur champ électrique
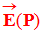 est tangent en tout
point.
est tangent en tout
point.
- La ligne de champ est orientée dans le sens du champ.
- Un ensemble de lignes de champ constitue un spectre.
- Champ créé par une charge ponctuelle :
-
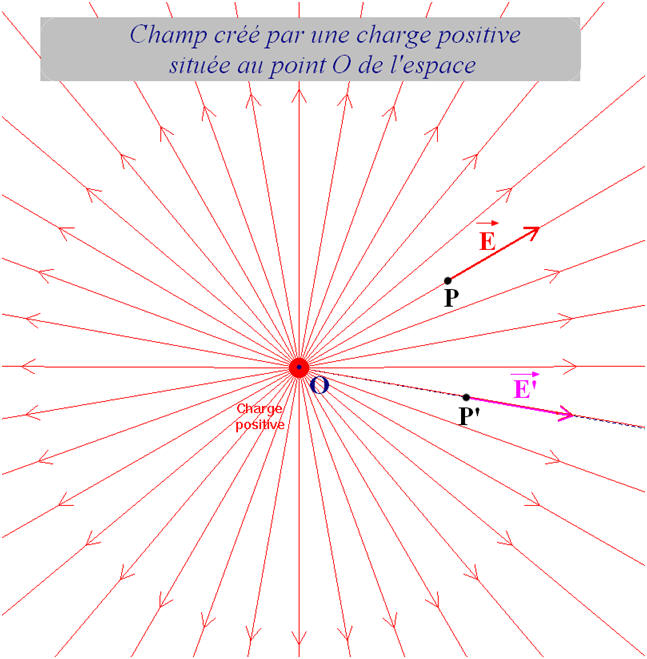
Premier cas : Q > 0
- Schéma :
Animation CabriJava
- Une charge ponctuelle positive placée au point O de l’espace crée un champ radial et centrifuge dans tout l’espace environnant.
- Deuxième cas : Q < 0
- Schéma :
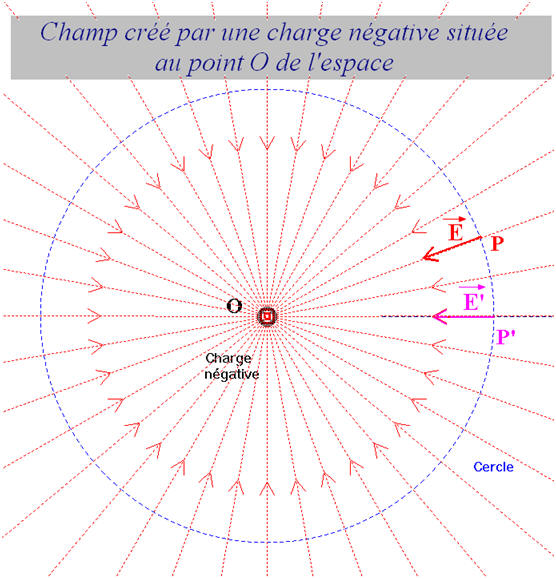
Animation CabriJava
- Une charge ponctuelle négative placée au point O de l’espace crée un champ radial et centripète dans tout l’espace environnant.
- Champ créé par deux charges ponctuelles.
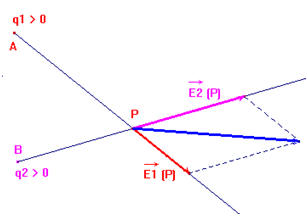
-
Le champ électrique
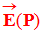 , créé par
plusieurs charges, en un point P de l’espace est égal à
la somme vectorielle des champs créés par chaque charge en P.
, créé par
plusieurs charges, en un point P de l’espace est égal à
la somme vectorielle des champs créés par chaque charge en P.
- on parle de champ résultant.
- Les champs électriques, grandeurs vectorielles, s’ajoutent comme des vecteurs.
4)- Champ électrique uniforme : le condensateur plan.
a)- Définition.
-
Un champ électrique est dit uniforme dans une région de
l’espace si le vecteur champ 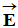 conserve
en tout point de cette région, la même direction, le même sens
et la même valeur.
conserve
en tout point de cette région, la même direction, le même sens
et la même valeur.
- Schéma :
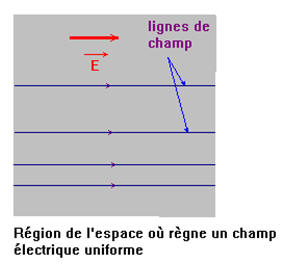
- Les lignes de champ sont des droites parallèles entre elles.
b)- Le condensateur plan.
► Description.
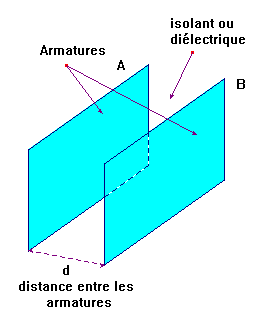
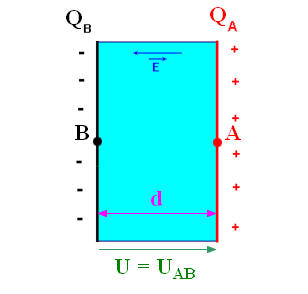
- Un condensateur plan est formé par deux plateaux conducteurs parallèles A et B appelés armatures, séparés par un isolant de faible épaisseur d.
- Schéma :
► Charge du condensateur :
- Pour charger un condensateur, on utilise un générateur de courant.
- Schéma :
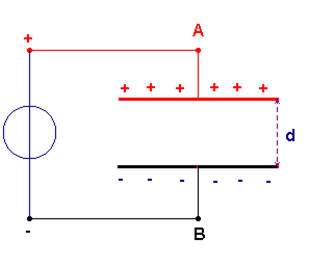
- Le générateur transfère les électrons d’une armature sur l’autre.
- On dit que le condensateur est chargé.
- Le courant ne circule que lors de la charge.
- Lorsque le condensateur est chargé, le courant ne circule plus.
- L’armature reliée à la borne plus du générateur porte la charge + Q > 0 : + Q = QA
- L’armature reliée à la borne moins du générateur porte la charge - Q < 0 : - Q = QB
- Entre les armatures existe la tension UAB = VA – VB > 0
- Q, grandeur positive, est appelée charge du condensateur.
- C’est la charge portée par l’armature positive du condensateur : + Q = QA = - QB
-
Dans l’espace situé entre les armatures, le champ
électrique 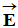 :
:
- Est considéré comme uniforme,
- Sa direction est perpendiculaire aux armatures,
- Son sens est dirigé de l’armature positive à l’armature négative (sens des potentiels décroissants),
-
Son intensité (sa valeur) :
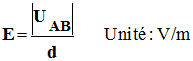
c)- Pour aller plus loin :
- Un champ électrique agit sur des particules chargées qu’elles soient immobiles ou en mouvement.
- Un champ électrique permet de dévier ou d’accélérer un faisceau d’électrons.
- C'est un dispositif qui accélère les électrons.
- Il comprend :
- Une plaque C appelée cathode (elle émet des électrons en utilisant l'effet thermoélectronique : le filament f chauffe la cathode pour émettre des électrons.
- Une plaque A appelée anode qui attire et accélère les électrons.
- Elle est percée d'un trou pour laisser passer les électrons.

- La tension UAC peut atteindre quelques dizaines de kilovolts.
- Le champ entre les deux plaques est uniforme et il est orienté de A vers C.
► Les plaques de déviation.
-
Les électrons pénètrent avec une
vitesse horizontale  à l'intérieur d'un condensateur plan dans
lequel règne le vide.
à l'intérieur d'un condensateur plan dans
lequel règne le vide.
- Entre les deux plaques horizontales A et B de ce condensateur, séparées par la distance d, est appliquée une tension UAB.
- On admet que le champ électrique qui en résulte agit sur les électrons sur une distance L mesurée à partir de O.
- Les électrons sont déviés vers le haut ou vers le bas suivant le signe de la tension UAB.
- Application : écran d’oscilloscope. étude de l'oscilloscope ; Tensions variables et oscilloscope
- Cours : Mouvement d’une particule chargée dans un champ électrique uniforme.
IV- Champs de pesanteur et de gravitation.
1)- Champ de pesanteur.
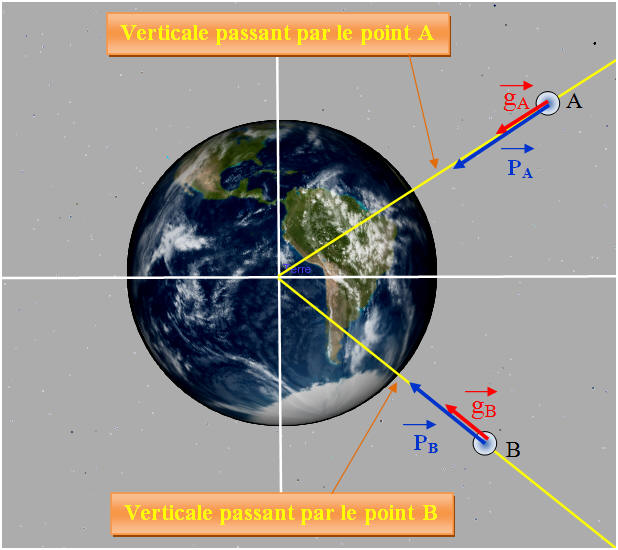
-
Au voisinage de la Terre, un objet de masse m,
situé au point A, est soumis à son poids
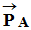 .
.
-
De même l’objet de masse m, situé au point B,
est soumis à son poids
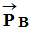 .
.
- Ceci provient du fait que la Terre de masse MT, crée dans son espace environnant un champ de pesanteur.
-
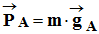 Et
Et
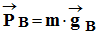
- Schéma :
- Le champ de pesanteur est un champ vectoriel.
-
La relation qui lie le champ de pesanteur
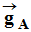 au point A et le
poids
au point A et le
poids
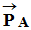 d’un objet de masse
m placé en ce point A est :
d’un objet de masse
m placé en ce point A est :
-
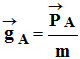
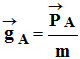
-
Caractéristiques de 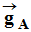 :
:
|
|
Origine : |
Point A |
|
La direction ; |
Verticale passant par le point A |
|
|
Le sens |
Vers la Terre |
|
|
L’intensité ou la valeur |
|
|
|
Unités : |
P en newton (N) m en kilogramme (kg) g en N / kg |
► Champ de pesanteur uniforme :
- Lorsque les dimensions sont de l’ordre du kilomètre, on peut considérer que le champ de pesanteur est uniforme.
- Sa valeur diminue d’environ 0,3 % si on s’élève de 10 km et sa direction varie d’environ 1° entre deux points distants de 100 km.
- Caractéristiques du champ local :
|
|
Origine : |
Quelconque |
|
La direction ; |
Verticale du lieu |
|
|
Le sens |
Vers la Terre |
|
|
L’intensité ou la valeur |
Elle dépend de l’altitude et de la latitude g = 9,81 N / kg à Paris |
- Schéma :
2)- Champ de gravitation.
-
Une masse M crée un champ de gravitation
 dans tout l’espace
environnant.
dans tout l’espace
environnant.
- Ce champ est mis en évidence grâce à l’interaction gravitationnelle qui existe entre la masse M, placée au point O de l’espace et la masse m, placée au point P de l’espace (Mesure de G par Cavendish : Expérience de Cavendish).
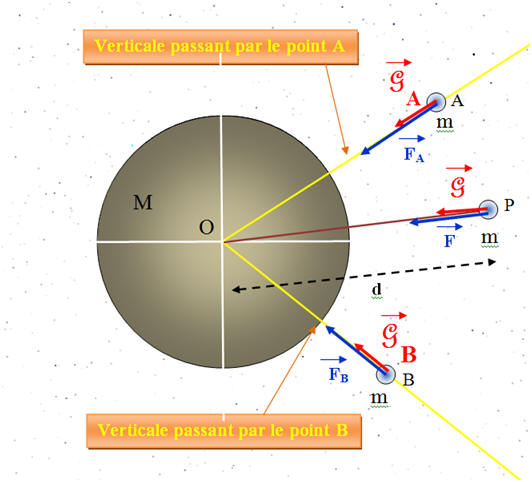
-
La masse m, située au point P de l’espace,
subit une force
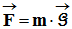
- Le champ de gravitation est un champ vectoriel.
-
La relation qui lie le champ de gravitation
 en un point P de
l’espace et la force d’attraction gravitationnelle
en un point P de
l’espace et la force d’attraction gravitationnelle
 qui s’exerce sur l’objet
de masse m situé au point P de l’espace est :
qui s’exerce sur l’objet
de masse m situé au point P de l’espace est :
-
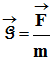
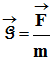
- Schéma :
-
Expression et valeur de la force
 :
:
-

|
|
Point d’application : P |
|
Direction : la droite (OP) |
|
|
Sens : de P vers O |
|
|
Valeur de la force :
|
-
Caractéristique de  :
:
|
|
Point d’application : P |
|
Direction : la droite (OP) |
|
|
Sens : de P vers O |
|
|
Valeur
|
|
|
Unité |
N / kg |
3)- Champ de gravitation et de pesanteur.
- À cause du mouvement de rotation de la Terre, le poids d’un objet, de masse m, n’est pas tout à fait identique à la force d’attraction gravitationnelle exercée par la Terre sur cet objet.
-
On toute rigueur, en un même point P de l’espace :
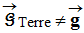
-
Mais la différence entre
 et
et
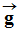 est faible.
est faible.
-
Lorsque la précision le permet, on identifie localement
le champ de pesanteur 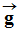 au
champ de gravitation de la Terre
au
champ de gravitation de la Terre
 .
.
-
Au voisinage de la Terre :
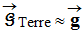
► Application :
- Calculer GTerre à la surface de la Terre :
- Comparer cette valeur à la valeur de g = 9,81 N / kg à Paris.
- Données :
-
MT
= 5,98
× 1024
kg ; RT = 6400
km ; G = 6,67
× 10–
11 S.I
- Valeur de GTerre à la surface de la Terre :
-
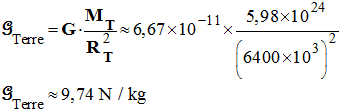
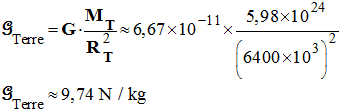
-
Incertitude relative : 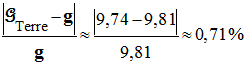
- L’écart est faible.
► Remarque
- La Terre est légèrement aplatie aux pôles :
-
Rayon équatorial : RT = 6380
km, valeur de GTerre
≈ 9,80 N / kg
- Rayon polaire : RT = 6360 km, valeur de GTerre ≈ 9,86 N / kg
![]() Conclusion :
Conclusion :
- Au voisinage de la Terre, le champ de pesanteur s’identifie au champ de gravitation si on néglige l’effet de la rotation de la Terre autour de l’axe des pôles.
V- Applications.
1)- QCM : Pour chaque question, indiquer la (ou les) bonne(s) réponse(s).
|
|
2)- Exercices : Exercices : énoncé avec correction
a)- Exercice 7 page 213. Cartographier un champ scalaire.
b)- Exercice 9 page 213. Exploiter des lignes de champ vectoriel.
c)- Exercice 11 page 213. Lire une carte de vitesse des vents.
d)- Exercice 12 page 213. Identifier les pôles magnétiques.
e)- Exercice 18 page 215. La Terre a rendez-vous avec la Lune.
f)- Exercice 20 page 215. Point d’équigravité.
g)- Exercice 24 page 217. Le temps est à l’orage.
h)- Exercice 25 page 217. Champ géomagnétique.
|
|