|
Phys. N° 11 |
Mouvements de projectiles. Cours. |
|
|
|
|
Programme 2012 : Cinématique et dynamique newtonienne Applications des lois de Newton et Kepler. Travail et énergie. Programme 2012 : Physique et Chimie Programme 2020 : Physique et Chimie |
|
I- Mouvement d’un projectile dans le champ de pesanteur.
|
|
II- Équations horaires paramétriques. 5)- Équation de la trajectoire. |
|
III- Influence des conditions initiales. |
|
QCM N° 05 |
Pour aller plus loin :
|
Mots clés : Mouvements ; champ de pesanteur ; conditions initiales ; portée ; flèche ; mouvement parabolique ; balistique ; ... |
I-
Mouvement
d’un projectile dans le champ de pesanteur.![]()
- Une bille est lancée avec la main avec une vitesse
![]() faisant un angle
α
avec le plan horizontal.
faisant un angle
α
avec le plan horizontal.
- Quel est le mouvement du centre d’inertie G de la bille dans le référentiel terrestre ?
- Vidéo : parabil.avi
|
Chute libre d'une balle avec vitesse initiale |

|
- Une étude chronophotographique permet d’étudier le mouvement de la bille dans un référentiel terrestre. - La Webcam est située dans un plan perpendiculaire à l’axe de visée. - Connaissant l’intervalle de temps
t entre deux images
et l’échelle, on peut déterminer les vecteurs vitesses
du centre d’inertie de la bille à différents instants et en déduire le vecteur accélération correspondant. - On vérifie, aux erreurs de construction près,
que le vecteur accélération
du mouvement et qu’il a même direction, mais sens et
même valeur que le vecteur
- En conséquence :
- On peut considérer que sur le petit parcours, la poussée d’Archimède et les forces de frottements sont négligeables devant le poids de la bille (il faut un objet de petite dimension dont la masse volumique est importante). |
|
- Lors du mouvement, la bille n’est soumise qu’à son poids. - Le vecteur accélération du centre d’inertie est égal au vecteur champ de pesanteur : La bille est en chute libre. |
II-
Équations horaires paramétriques.![]()
|
énoncé. Une balle de tennis de masse m est lancée d'un point O
avec une vitesse initiale
On considère que la balle est en chute libre. Données : v0 =12 m / s ; α = 60 ° ; m = 50 g et g = 9,81 m / s².
On choisit comme repère :
orienté vers le haut et x'Ox axe horizontal orienté de gauche à droite.
Le plan
(x'x,
y'y) contient le vecteur vitesse
Les vecteurs
On choisit comme origine des espaces le point O et l'origine des dates l'instant ou la balle occupe la position O. - Donner les équations horaires du mouvement. Que peut-on dire du mouvement de G suivant l'axe x'Ox, suivant l'axe y'Oy. - Dans quel plan s'effectue le mouvement de G ? - Déterminer l'équation de la trajectoire du point G. Conclusion. - Déterminer la portée horizontale (distance OC : les points O et C sont situés sur la même horizontale). - Donner l'expression littérale puis la valeur numérique. - Quelle doit être la valeur de l'angle α pour que la portée horizontale soit maximale ? - Déterminer la flèche c'est-à-dire l'altitude maximale atteinte par le projectile. - Donner l'expression littérale puis la valeur numérique. - Recommencer les calculs pour α = 30 ° et tirer les conclusions. |
- Le système : la balle de masse m et de centre d'inertie G.
- Le référentiel : référentiel terrestre considéré comme galiléen car cette courte durée, on peut considérer que la terre n'a pas bougé.
- Le repère d'espaces lié au référentiel d'étude :
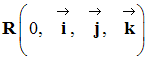
- Conditions initiales :


- Bilan des forces : la balle est soumise à son poids
![]() .
.
- On peut négliger la poussée d’Archimède et les forces de frottements.
- Deuxième loi de Newton (Théorème du centre d'inertie) :
- 
- équations horaires du mouvement
- Coordonnées du vecteur accélération :
|
|
De l’équation (1), on tire |
|
- Coordonnées du vecteur vitesse.
-
On utilise la relation
 .
.
- On cherche les primitives des équations précédentes.
- Il apparaît des constantes qui sont liées aux conditions initiales.
|
|
D’après les conditions initiales |
|
- Coordonnées du vecteur position.
- On opère de la même façon :

|
|
D’après les conditions initiales |
|
- Le mouvement suivant l'axe x'Ox est rectiligne uniforme.
- Le mouvement suivant l'axe y'Oy est rectiligne uniformément varié.
- Le mouvement de G est contenu dans le plan (x'x, y'y) appelé plan de tir.
-
Il contient le vecteur
![]() .
.
5)- Équation de la trajectoire.
- On élimine le temps t entre pour trouver la relation entre x et y : y = f (x).
|
|
On déduit l’équation de la trajectoire |
|
-
La trajectoire de
G est une portion de
parabole contenue dans un plan vertical contenant le vecteur vitesse
![]() .
.
6)- Simplification de l'équation.
- On va utiliser le fait que la trajectoire est une portion de parabole.
- On utilise les propriétés des paraboles.
- Pour simplifier l'exercice, on pose :
-

- avec : m = – 0,136 m – 1 et b = 1,73
- l'équation à étudier est plus simple.
- il faut calculer la longueur OC, en conséquence il faut trouver l'abscisse du point C tel que
- ![]()
- Il faut résoudre l‘équation (2).
- ![]()
- On rejette la solution xC = 0
- Pour trouver l'expression littérale générale, on remplace b et m par leurs valeurs respectives.
- 
- Application numérique :
-

- Valeur de l'angle :
- pour que la portée horizontale soit maximale :
- sin 2 α = 1 => α = 45 °
- Dans ce cas xC ≈ 14,7 m
- On utilise la propriété de la parabole :
- ![]() avec
avec

- altitude maximale :
- 
- Autre méthode :
- c'est l'altitude maximale en conséquence :
-

- On travaille avec l'expression simplifiée :
- 
- altitude maximale :
-

- En remplaçant b et m par leurs expressions respectives :
- 
- Application numérique :
- 
- Recommencer les calculs pour α = 30 ° et tirer les conclusions.
III-
Influence des conditions initiales.![]()
1)- Exploitation de l’animation :
- On peut faire varier la valeur de la vitesse initiale et on peut faire varier la valeur de l’angle α que fait le vecteur vitesse avec l’horizontale.
- Pour une même valeur de l’angle α, plus la valeur de la vitesse initiale est grande et plus la flèche et la portée sont grandes.
- Pour une même valeur de la vitesse, la portée est maximale pour un angle de tir de 45 °.
- Pour une même valeur de la vitesse, des angles de tir complémentaires ont même portée.
|
QCM N° 05 |