I- Danger en spéléologie.

1)- Introduction.

-  Lors de l’exploration d’une grotte, un spéléologue peut rencontrer des nappes de dioxyde de carbone.

-  À teneur élevée, ce gaz entraîne des évanouissements et même la mort.

-  Le dioxyde de carbone est formé par action d’eaux de ruissellement acides sur le carbonate de calcium CaCO₃ présent dans les roches calcaires.

Données : Système S₁ = {Voiture}

► Température du laboratoire au moment de l’expérience : θ = 25 ° C

► Pression atmosphérique : P_atm = 1,013 × 10⁵ Pa

► Le dioxyde de carbone formé se comporte comme un gaz parfait et vérifie la loi des gaz parfaits :

► P . V (CO₂) = n (CO₂) . R . T

► Les unités : P en Pa ; V (CO₂) en m³ ; n (CO₂) en mol ; T en K.

► Constante des gaz parfaits : R = 8,31 J . mol^-1 . K^-1

2)- Résultat de l’expérience :

-  Un élève verse dans un ballon, une solution de volume V_S = 100 mL d’acide chlorhydrique de concentration en quantité d’ions oxonium C_S = 100 mmol . L^-1.

-  À la date t = 0 s, il introduit rapidement dans un ballon un échantillon de carbonate de calcium CaCO₃ (s) de quantité de matière n₀ = 20,0 mmol

-  et déclenche simultanément un chronomètre.

-  Puis il relève les valeurs du volume V (CO₂) de dioxyde de carbone dégagé en fonction du temps t.

-  Ces valeurs sont reportées dans le tableau ci-dessous.

-  La pression du gaz est égale à la pression atmosphérique.

-  La transformation chimique étudiée est modélisée par la réaction d’équation :

CaCO₃ (s) + 2 H₃O⁺ (aq) → Ca²⁺ (aq) + CO₂ (g) + 3 H₂O (ℓ)

3)- Questions :

a)-  Construire le tableau d’avancement de la réaction et déterminer la valeur de l’avancement maximal noté x_max.

-  Détermination de la valeur de l’avancement maximal x_max :

-  Les réactifs : les ions oxonium présents dans la solution d’acide chlorhydrique :

-  Formule de la solution d’acide chlorhydrique : (H₃O⁺ (aq) + Cℓ^- (aq))

-  Quantité de matière d’ions oxonium H₃O⁺ : (attention aux unités)

-  n₁ = C_S . V_S

-  n₁ = 100 × 100 × 10^-3

-  n₁ = 10,0 mmol

-  Quantité de matière de carbonate de calcium CaCO₃  :

-  n₀ = 20,0 mmol

-  Valeur de l’avancement maximal :

-  La réaction est supposée totale : x_f = x_max 

-  Hypothèse 1 : On considère que le réactif limitant est l’ion oxonium H₃O⁺ (aq) :

-  n₁ – 2 x_max1 = 0

-  10,0 – 2 x_max1 = 0 => x_max1 = 5,00 mmol

-  Hypothèse 2 : On considère que le réactif limitant est le carbonate de calcium CaCO₃ (s) :

-  n₀ – x_max2 = 0

-  20,0 – x_max2 = 0 => x_max2 = 20,0 mmol

-  x_max = x_max1 = 5,00 mmol < x_max2

-  Réactif limitant : le réactif limitant est l’ion oxonium H₃O⁺ (aq).

-  On peut maintenant compléter le tableau d’avancement :

b)-  Exprimer l’avancement x de la réaction à une date t en fonction de V (CO₂), T, P_atm et R.

-  La lecture du tableau d’avancement permet de donner la relation suivante :

-  n (CO₂) = x

-  On considère que le dioxyde de carbone formé se comporte comme un gaz parfait et vérifie la loi des gaz parfaits :

-  P . V (CO₂) = n (CO₂) . R . T

-   

-  Au cours de l’expérience :

-  P = P_atm = 1,013 × 10⁵ Pa et T = θ + 273

-  Dans les conditions de l’expérience, on peut écrire :

-   

c)-  Calculer le volume maximal V_max de gaz susceptible d’être recueilli dans les conditions de l’expérience. Déterminer si la transformation est totale.

-  Volume maximal V_max de gaz susceptible d’être recueilli dans les conditions de l’expérience :

-  C’est le volume recueilli lorsque l’avancement de la réaction est égal à l’avancement maximal.

-   

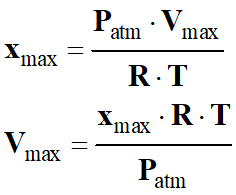
-  Application numérique :

-   

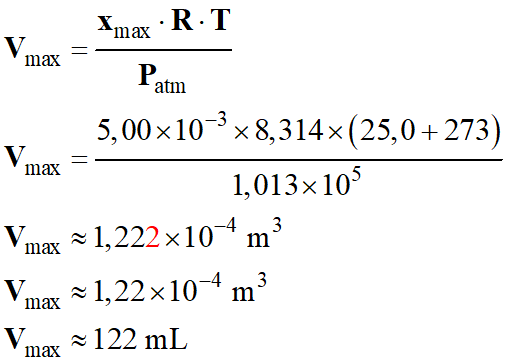
-  Caractéristique de cette transformation :

-  La consultation du tableau permet de noter la valeur du volume de dioxyde de carbone obtenu en fin de réaction :

-  V (CO₂)_{t = 440 s} = 121 mL

-  On peut considérer que l’état final correspond à l’état d’avancement maximal de la réaction.

-  La réaction est lente, mais elle est considérée comme totale.

d)-  Représenter le nuage de points expérimentaux obtenu en plaçant la date t en abscisse et l’avancement x en ordonnée.

-  Représentation graphique de la transformation.

-  Pour le calcul de l’avancement x en fonction du volume V (CO₂)_t

-   

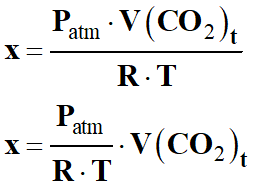
-  Les unités : On veut calculer l’avancement x en mmol et exprimer le volume en mL

-   

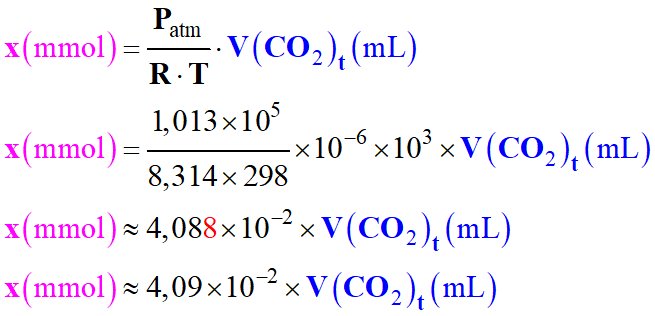
-  Avec le tableur Excel :

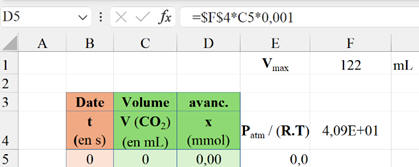
-  Dans la cellule D5, on tape l’expression suivante : =$F$4*C5*0.001

-  Puis on recopie cette expression vers le bas autant de fois que nécessaire.

-  Pour ce faire : On sélectionne la cellule concernée (ici la cellule D5).

-  On se place en bas à droite de cette cellule avec la souris

-  Lorsque le signe plus (+) apparaît, on réalise un double clic gauche (souris).

- Le calcul s’effectue.

- Tableau de valeurs :

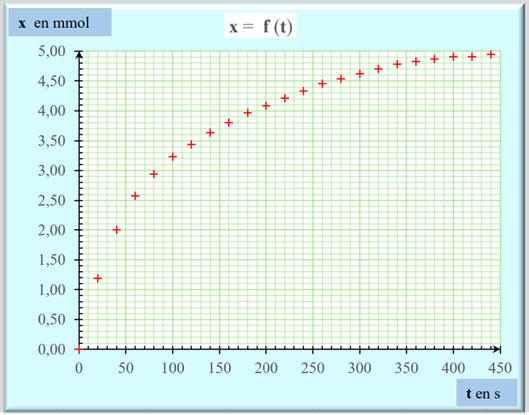
-  Représentation graphique :

-  L’avancement x de la réaction est une fonction croissante du temps t.

-  La variation de l’avancement x de la réaction diminue au cours du temps pour s’annuler en fin de réaction.

e)-  Décrire l’évolution de la vitesse volumique de formation de CO₂ au cours du temps.

-  Description de l’évolution de la vitesse volumique de formation de CO₂ au cours du temps :

-  Avancement de la réaction : x = n (CO₂)

-  Vitesse volumique de la réaction : en utilisant l’avancement x de la réaction

-  Par définition :

-  La vitesse volumique de réaction v (t) à la date t, est la dérivée par rapport au temps,

-  Du rapport entre l’avancement x de la réaction et le volume V_S du milieu réactionnel.

-   

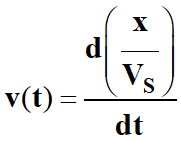
-  Lorsque l’on travaille à volume constant, on obtient la relation suivante :

-  Relation :

-   

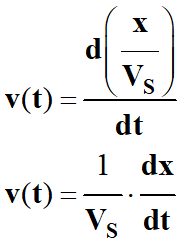
-  Au cours du temps, la vitesse volumique de la réaction diminue car la variation de l’avancement de la réaction diminue

-  Vitesse d'apparition d'un produit .

La vitesse d’évolution d’un système.

- 

-  La vitesse v_app (P) d’apparition du produit P, à la date t₁ est, par définition, égale à la dérivée de la fonction n_p = f (t) au temps t₁.

-  On écrit :

- 

-  Graphiquement : cette vitesse est numériquement égale à la valeur du coefficient directeur de la tangente T à la courbe n_p = f (t) au point M₁ d'abscisse t₁.

-  Si le mélange réactionnel a un volume constant V au cours de la réaction, on peut dans ce cas suivre l'évolution de la réaction en travaillant avec les concentrations :

-  On peut alors travailler avec la vitesse volumique d’apparition du produit P :

-  Par définition :

-   

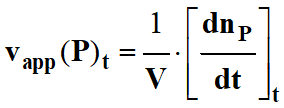
-  Dans le cas du dioxyde de carbone, on peut écrire :

-   

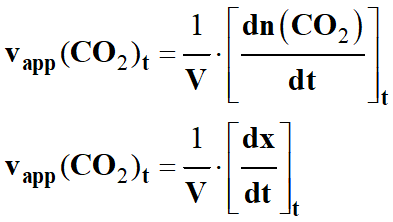
-  À la lecture du graphique, on remarque que la pente de la tangente à la courbe diminue au cours du temps.

-  La vitesse volumique d’apparition d’un réactif ou de disparition d’un produit diminue au cours du temps.

-  La courbe x = f (t) tend vers une asymptote horizontale et le coefficient directeur de la tangente à la courbe tend vers zéro.

-  La vitesse d’une transformation chimique est maximale à l’instant initial.

-  Elle décroît ensuite et s’annule lorsque la réaction est terminée.

-  Les réactifs sont consommés au fur et à mesure que la réaction se poursuit.

-  Comme la concentration des réactifs est un facteur cinétique, la diminution de la concentration des réactifs entraîne la diminution de la vitesse.

-  Elle s’annule si le réactif limitant à totalement disparue.

f)-  Définir le temps de demi-réaction t_1/2 . Déterminer graphiquement sa valeur.

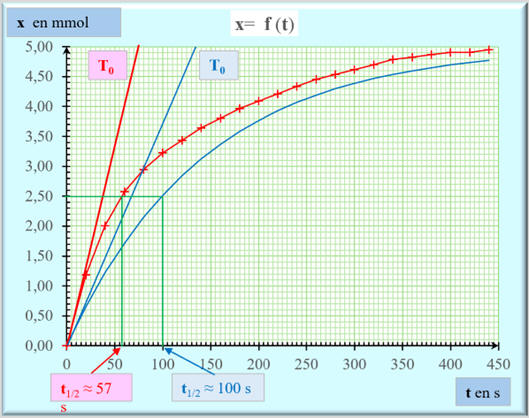
-  Le temps de demi-réaction :

-  Le temps de demi-réaction t_1/2 d’un système chimique est la durée au bout de laquelle la moitié du réactif limitant a été consommé.

-  Réactif limitant : le réactif limitant est l’ion oxonium H₃O⁺ (aq).

-  On peut déterminer t_1/2 à partir de l’évolution de la quantité de matière n_P ou de la concentration d’un produit P au cours du temps :

-  Le temps de demi-réaction t_1/2 est la date pour laquelle :

-   

-  Dans le cas présent :

-   ou

-  Exploitation graphique :

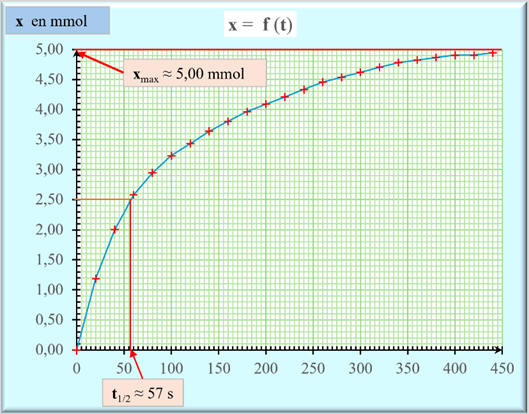
-  t_1/2 ≈ 57 s

-  Le temps de demi-réaction t_1/2 permet d’évaluer la durée nécessaire à l’achèvement de la transformation chimique étudiée.

-  L’expérience montre qu’un système siège d’une réaction caractérisée par le temps de réaction t_1/2 cesse pratiquement d’évoluer au bout d’une durée de l’ordre de quelques t_1/2 (4 à 7 suivant la précision recherchée).

-  Dans le cas présent, on peut considérer que la réaction est terminée au bout de 400 s ( 7 ×57) environ.

g)-  La température de la grotte est généralement inférieure à 25 ° C. Préciser l’effet de cet abaissement de la température sur la vitesse volumique initiale de formation de CO₂.

-  Effet de cet abaissement de la température sur la vitesse volumique initiale de formation de CO₂.

-  La température fait partie des facteurs cinétiques.

-  De façon générale, une diminution de la température a pour effet de ralentir l’évolution temporelle d’une réaction chimique.

-  En conséquence, l’abaissement de la température entraîne une diminution de la vitesse initiale de formation du dioxyde de carbone.

h)-  Compléter le graphique réalisé à la question d)-, en représentant l’allure de l’évolution de l’avancement en fonction du temps dans ce cas.

-  Allure de l’évolution de l’avancement en fonction du temps :

- 

Chimie et spéléologie

Temps et évolution chimique : cinétique et catalyse. . (2012)

Facteurs cinétiques

Application : Suivi cinétique d'une réaction chimique - Exploitation des résultats avec Latis-Pro

Modélisation macroscopique de l'évolution d'un système.

Suivi cinétique par spectrophotométrie.

Vitesse d’une réaction chimique (2000)

Suivi temporel d'une réaction chimique.

Modélisation macroscopique de l'évolution d'un système.

Vieillissement d'une eau de Javel 

II- Un colorant pour traiter des infections.

1)- Introduction

-  Le vert de malachite est un composé de formule C₂₃H₂₅ClN₂ utilisé comme colorant.

-  En solution aqueuse, il forme les ions chlorure Cl^- (aq) et les ions carbénium C₂₃H₂₅N₂⁺ (aq), noté M⁺ (aq).

-  Toxique, le vert de malachite a pu aussi être utilisé pour traiter les infections fongiques et bactériennes.

-  En milieu basique, l’ion M⁺ (aq) réagit avec l’ion hydroxyde HO^- (aq) entraînant la décoloration de la solution suivant une transformation totale dont l’équation de réaction s’écrit :

M⁺ (aq)  + HO^- (aq) → MOH (aq)

-  La vitesse de consommation de l’ion M⁺ (aq) peut s’écrire :

-  V_c (M⁺) = k . [HO^-]^α . [M⁺]^β

-  Les grandeurs α et β sont des entiers.

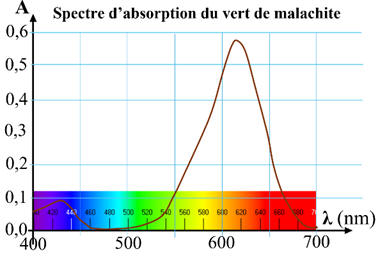
-  Seule l’espèce M⁺ absorbe dans le domaine du visible.

-  Solution de soude : Na⁺ (aq) + HO^- (aq)

-  Spectre d’absorption du vert de malachite :

-  Disque chromatique :

-  Couleur d’une solution de vert de malachite :

2)- Expérience 1 :

a)-  Protocole :

  Une solution est préparée en introduisant :

-  20,0 mL d’une solution aqueuse de vert de malachite 

-  De concentration en quantité d’ion carbénium C (M⁺) = 75,0 μmol . L^-1 ;

-  75, 0 mL d’eau distillée.

  En déclenchant simultanément le chronomètre, on ajoute :

-  Un volume V =5,00 mL d’une solution de soude

-  De concentration en quantité de matière d’ion hydroxyde C (B) = 100 mmol . L^-1.

b)-  Résultats expérimentaux.

-  Les concentrations en quantité initiales respectives des espèces M⁺ (aq) et HO^- (aq) après mélange sont notées :

-  [HO^-]₀ et [M⁺]₀

-  L’absorbance A (t) à une longueur d’onde λ judicieusement choisie est mesurée à différentes dates.

-  Tableau de valeurs :

3)- Expérience 2 :

a)-  Protocole :

-  L’expérience précédente est renouvelée en modifiant la concentration, C (B) de la solution de soude.

-  Les volumes de solutions utilisées et la concentration en quantité d’ion M⁺ restent identiques.

-  Une analyse des résultats permet de construire le tableau ci-dessous, fournissant la valeur de :

-   k . [HO^-]^α pour les différentes valeurs de C (B).

b)-  Résultats expérimentaux :

4)- Questions :

a)-  En considérant l’expérience 1, calculer les concentrations en quantité de matière initiales des espèces M⁺ et HO^- après le mélange.

-  Concentrations en quantité de matière initiales des espèces M⁺ et HO^- après le mélange :

-  Le mélange :

-  Solution aqueuse de vert de malachite : V₁ = 20,0 mL et C (M⁺) = 75,0 μmol . L^-1 

-  Eau distillée : V = 75,0 mL

-  Solution de soude : V₂ = 5,00 mL et C (B) = 100 mmol . L^-1

-  Concentration des différentes espèces présentes à l’instant initial (avec réaction) :

-  La concentration molaire volumique d’une espèce chimique en solution est la quantité de matière n de soluté présente dans un litre de solution.

-  Espèces présentes dans la solution :

-  M⁺ (majoritaire) et HO^- (majoritaire), le solvant,  l’eau (ultra-majoritaire) et les ions sodium Na⁺ (majoritaire) présents dans la soude.

-  Volume de la solution :

-  V_S = V + V₁ + V₂

-  V_S = 75,0 + 20,0 + 5,00

-  V_S ≈ 100 mL

-  Concentration initiale en ions carbénium M⁺ (aq) :

-   

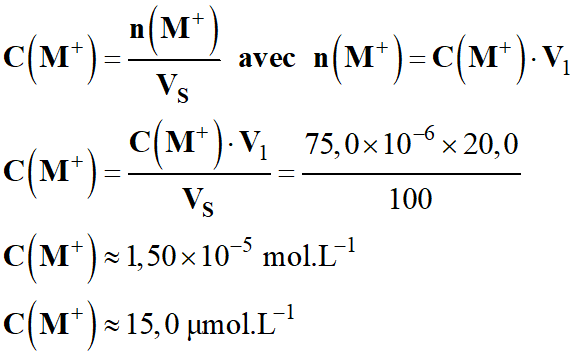
-  En conséquence :

-  [M⁺]₀ ≈ 15,0 μmol . L^-1

-  Concentration initiale en ions hydroxyde HO^- (aq) :

-   

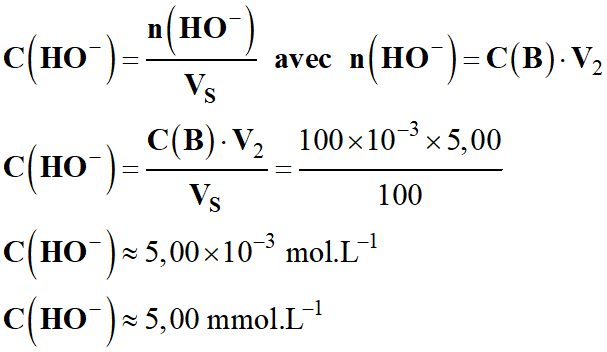
-  [HO^-]₀ ≈ 5,00 mmol . L^-1

-  On remarque que [HO^-]₀ >>  [M⁺]₀

b)-   Montrer que la grandeur k . [HO^-]^α est presque constante au cours de la transformation. Par la suite, elle est notée k_app.

-  Évolution de la grandeur k . [HO^-]^α au cours du temps t.

-  Lors du mélange, il se produit la réaction suivante :

M⁺ (aq)  + HO^- (aq) → MOH (aq)

-  Cette réaction est considérée comme totale et l’espèce HO^- (aq) est en large excès par rapport à l’espèce M⁺ (aq).

-  Tableau d’avancement de la réaction :

-  Quantité de matière initiale en ions carbénium M⁺ :

-  n₁ = n (M⁺) = C (M⁺) . V₁

-  n₁ = n (M⁺) = 75,0 × 10^-6 × 20,0 × 10^-3

-  n₁ = n (M⁺) = 1,50 μmol

-  Quantité de matière initiale en ions hydroxyde HO^- (aq) :

-  n₂ = n (HO^-) = C (B) . V₂

-  n₂ = n (HO^-) = 100 × 10^-3 × 5,00 × 10^-3

-  n₂ = n (HO^-) = 1,50 μmol

-  L’ion carbénium est le réactif limitant. La réaction s’arrête lorsqu’il est totalement consommé.

-  x_max = n₂ = n (HO^-) = 1,50 μmol

-  Dans le mélange réactionnel, la quantité de matière ions hydroxyde varie 1,5 pour 500, c’est-à-dire de 3 pour mille.

À l’instant initial : [HO^-]₀ ≈ 5,00 mmol . L^-1

-  En fin de réaction :

-   

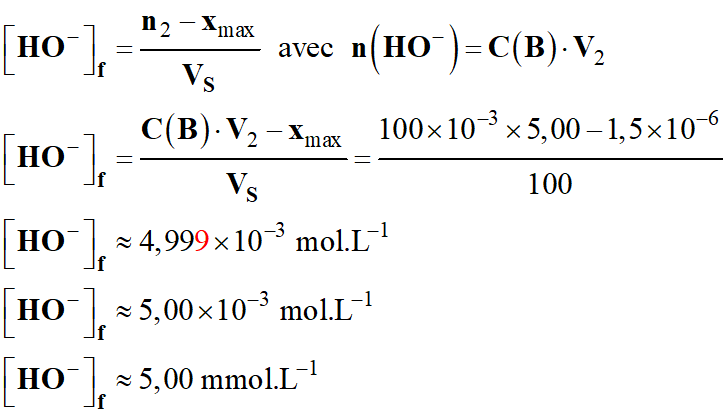
-  [HO^-]_f ≈ 5,00 mmol . L^-1

-  On peut revenir à la relation suivante :;

-   

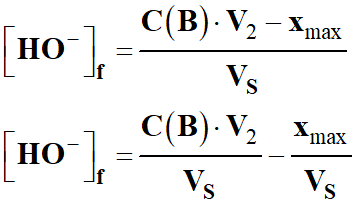
-  On divise l’expression par [HO^-]₀

-   

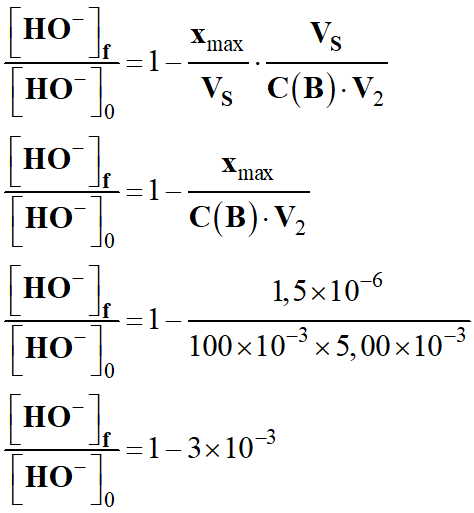
-  On peut considérer que :

-   

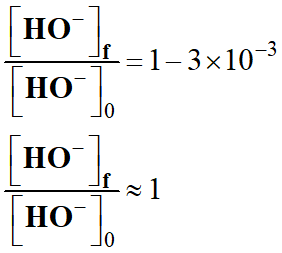
-  La grandeur k . [HO^-]^α est pratiquement constante au cours de la transformation.

c)-  Déterminer alors l’expression de la vitesse de consommation de M⁺ en fonction de k_app, [M⁺] et β.

-  Expression de la vitesse de consommation de M⁺ en fonction de k_app, [M⁺] et β :

-  La vitesse de consommation de l’ion M⁺ (aq) peut s’écrire :

-  V_c (M⁺) = k . [HO^-]^α . [M⁺]^β avec k_app = k . [HO^-]^α = cte

-  V_c (M⁺) = k_app . [M⁺]^β

d)-  Exprimer 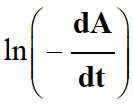en fonction de A, β, k_app, ainsi que le coefficient d’absorption molaire de M⁺, noté ε et la longueur ℓ de la solution traversée par le faisceau de lumière.

Loi de Beer - Lambert

- 

-  Pour les solutions suffisamment diluées, l’absorbance A est proportionnelle à la concentration C de l’espèce colorée.

►  Définition :

-  ε (λ) est appelé coefficient d’extinction molaire ou coefficient d’absorption molaire

-  Il dépend de la nature de l’espèce dissoute et de la longueur d’onde de la radiation utilisée.

-  La courbe A = f (C) constitue la courbe d’étalonnage de la substance étudiée.

-  Elle permet de déterminer la concentration d’une solution de la substance étudiée.

-  Elle permet donc de doser une espèce chimique colorée.

-  Afin d’augmenter la sensibilité de la méthode, on utilise la longueur d’onde qui correspond au maximum d’absorption de la substance étudiée.

-  Cette méthode est alors beaucoup plus précise que la méthode colorimétrique utilisant une échelle des teintes.

-  Remarque : la solution colorée doit être suffisamment diluée, 

-  C ≤ 1,0 × 10^–2 mol . L^–1, et le spectrophotomètre ne doit pas saturer.

-  Plus simplement, on peut donner la relation de Beer-Lambert suivante :

-  A = ε . ℓ . C

-  Comme la seule espèce colorée est l’ion carbénium M⁺ :

-  A = ε . ℓ . [M⁺]

Vitesses volumiques

►  Vitesse volumique de disparition d’un réactif R :

-  La vitesse v_disp (R)_t de disparition, d’un réactif R, est égale à l’opposé de la dérivée par rapport au temps de sa concentration :

-   

-  Vitesse volumique de disparition de l’ion carbénium M⁺ :

-   

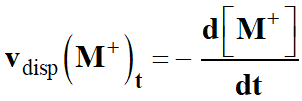
-  Avec les notations de l’énoncé :

-   

-   

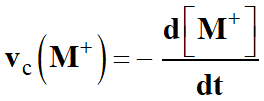
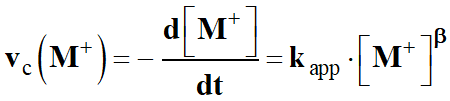
-  On utilise maintenant les propriétés de la fonction logarithme népérien.

-   

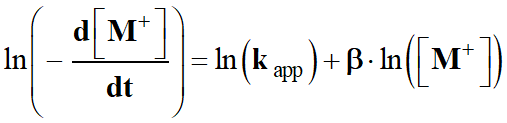
-  À partir de la loi de Beer-Lambert, on obtient l’expression suivante :

-  A = ε . ℓ . [M⁺]

-   

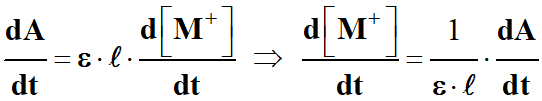
-  On remplace 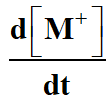par son expression :

-   

-   

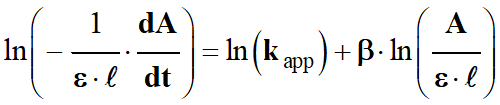
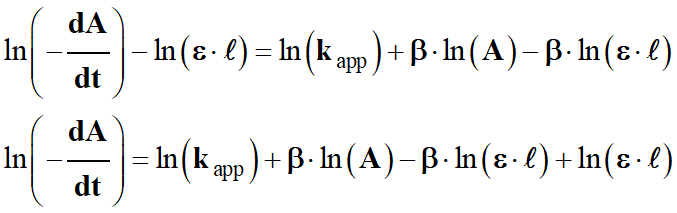
-  On regroupe les constantes ε, ℓ et k_app dans un même terme :

-   

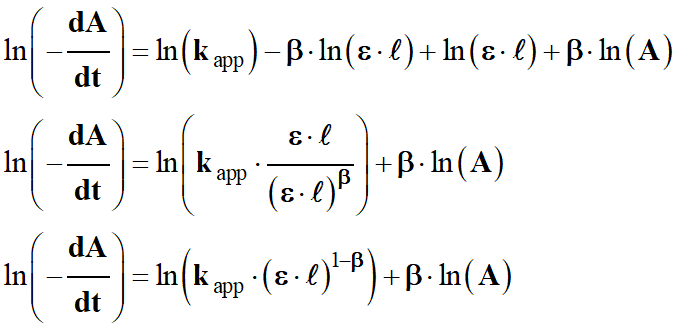
-  On est en présence d’une équation du type :

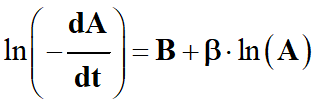-  avec

e)-  Déterminer la valeur de β par l’analyse des résultats expérimentaux.

-  Tableau de valeurs :

-  On effectue une régression linéaire de 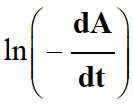 en fonction de ln A.

Droite de régression

-  Droite de régression.

-  Graphique :

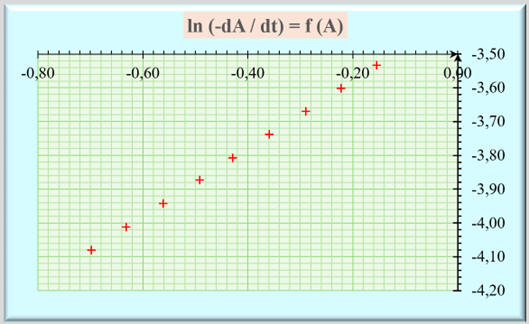
-  Les points sont sensiblement alignés.

-  On effectue une étude statistique avec le tableur Excel :

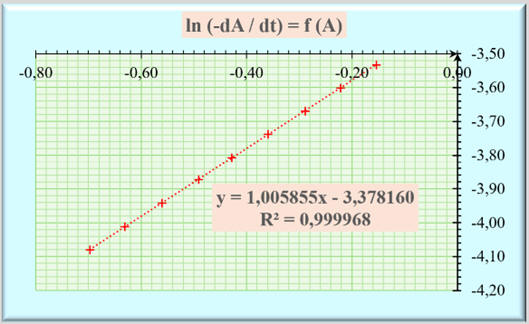
-  Traduction physique de l’équation donnée par le tableur Excel :

-   

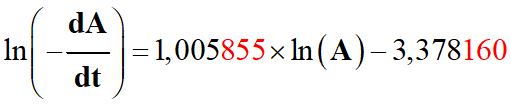
-  En gardant un nombre raisonnable de chiffres significatifs :

-   

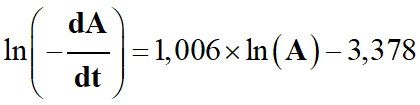
-  Valeur de la constante béta :

-  β ≈ 1,006 avec un coefficient de détermination R² ≈ 0,999968 ≈ 1,000

-  La corrélation est excellente entre 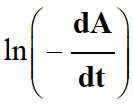 et ln (A).

-  Comme β est un entier : β = 1

f)-  À partir des résultats expérimentaux de l’expérience 2, déterminer les valeurs de α et de k.

M⁺ (aq)  + HO^- (aq) → MOH (aq)

-  La vitesse de consommation de l’ion M⁺ (aq) peut s’écrire :

-  V_c (M⁺) = k . [HO^-]^α . [M⁺]^β

-  De l’expérience 1, on tire :

-  V_c (M⁺) = k . [HO^-]^α . [M⁺]

-  D’autre part :

-  V_c (M⁺) = V_c (HO^-) = k . [HO^-]^α . [M⁺]

-  Avec  :

-   

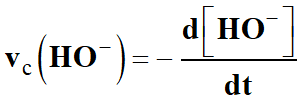
-  Les grandeurs α et β sont des entiers.

-  Résultats expérimentaux :

-  Quantité de matière initiale en ions hydroxyde HO^- (aq) :

-   n_i (HO^-) = C (B) . V₂

-  Concentration initiale en ions hydroxyde HO^- (aq) :

-   

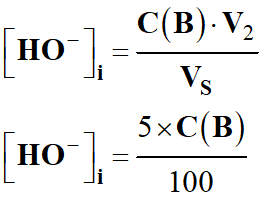
-  On va vérifier si une corrélation existe entre les grandeurs ln ([HO^-]) et ln (k . [HO^-]^α)

-  Pour simplifier la relation, on utilise la fonction logarithme népérien :

-  ln (k . [HO^-]^α) = k + α × ln ([HO^-])

-  Tableau de valeurs :

-  Pour faire une régression linéaire, le nombre de valeurs est dans ce cas très limité (3 valeurs).

-  Représentation graphique :

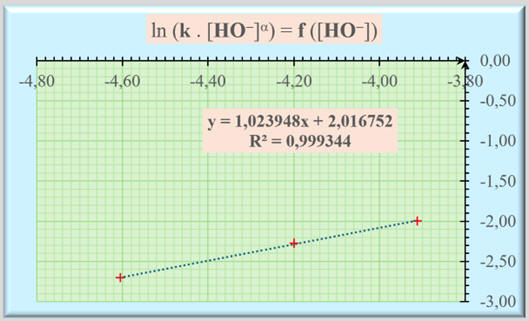
-  L’exploitation statistique permet d’écrire la relation suivante :

-  ln (k . [HO^-]^α) ≈ 2,016752 + 1,023948 × ln ([HO^-])

-  ln (k . [HO^-]^α) ≈ 2,01 + 1,02 × ln ([HO^-])

-  Comme la grandeur α est un nombre entier : α = 1

-  k ≈ 2,01

-  On peut donner l’expression de la vitesse de consommation de l’ion M⁺ (aq) :

-  V_c (M⁺) = k . [HO^-] . [M⁺]

-  Si la quantité de matière d’ions hydroxyde est en large excès par rapport à la quantité de matière d’ions carbénium, alors :

-  V_c (M⁺) = k_app . [M⁺]

Loi de vitesse d’ordre 1

- 

-  Considérons la réaction chimique suivante :

a A + b B → c C + d D

-  Une réaction chimique est d’ordre 1 par rapport au réactif A, si lorsque le réactif B est en large excès, les vitesses volumiques de disparition des réactifs ou d’apparition des produits sont proportionnelles à la concentration [A]_t de l’espèce A au cours du temps :

-  Ainsi, on peut écrire :

-   

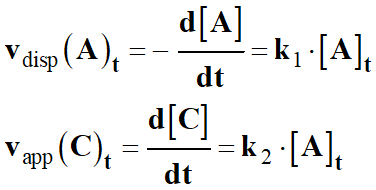
-  Pour la réaction étudiée :

M⁺ (aq)  + HO^- (aq) → MOH (aq)

-   

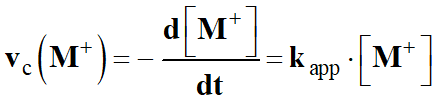
-  La réaction étudiée est ordre 1 par rapport à l’ion carbénium.