Modélisation macroscopique

de l'évolution d'un système

Cours

Exercices

Exercices 2023

L’éthanoate d’éthyle C₄H₈O₂ (ℓ) est un solvant mais il est rarement utilisé en raison de sa réactivité avec les bases.

Il peut réagir avec les ions hydroxyde HO^– (aq) selon la réaction, totale, lente, d’équation :

C₄H₈O₂ (ℓ) + HO^– (aq) → C₂H₃O₂^– (aq) + C₂H₆O (aq)

Un étudiant en chimie souhaite tester la réactivité de l’éthanoate d’éthyle avec les ions hydroxyde afin de savoir

si cette réaction est suffisamment lente pour pouvoir utiliser l’éthanoate d’éthyle en milieu basique.

►  Matériel et produits disponibles :

-  Solution d’hydroxyde de sodium : Na⁺ (aq) + HO^– (aq)

-  Concentration : C₀ = 2,5 × 10^–2 mol . L^–1

-  Éthanoate d’éthyle pur ;

-  Béchers de 100 mL et 200 mL,

-  Conductimètre, agitateur magnétique ;

-  Pipettes jaugées de 2,0 mL et 20 mL

-  Poire à pipeter (propipette), chronomètre,

-  Éprouvettes graduées de 10 mL et 100 mL ;

-  Pipette graduée de 5 mL ;

-  Ordinateur avec tableur.

1.  Justifier qu’il est possible de réaliser le suivi cinétique en utilisant la variation au cours du temps de la conductivité du mélange réactionnel.

2.  Proposer un protocole expérimental détaillé permettant d’effectuer le suivi cinétique dans le cas d’un mélange

d’un volume V₀ = 20,0 mL). d’hydroxyde de sodium de concentration C₀,

de 80,0 mL d’eau distillée

et de 2,0 mL d’éthanoate d’éthyle pur (en excès).

-  Données :

-  Conductivités molaires ioniques à 25 ° C en S . m² . mol^–1 :

-  λ (C₂H₃O₂^–) = 4,09 × 10^–3 ; λ (HO^–) = 19,9 × 10^–3 ; λ (Na⁺) = 5,01× 10^–3 

-  Dilution due à l’ajout de l’éthanoate d’éthyle : négligée.

-  Masse molaire de l’éthanoate d’éthyle : M₁ = 88,11 g . mol^–1

-  Masse volumique de l’éthanoate d’éthyle : ρ₁ = 0,902 g . mL^–1.

-  Masse molaire : M₁ = 88,11 g . mol^–1

-  Formule semi-développée :

-  Formule topologique :

-  Représentation 3D :

Réaction entre l’éthanoate d’éthyle et les ions hydroxyde HO^– (aq) :

C₄H₈O₂ (ℓ) + HO^– (aq) → C₂H₃O₂^– (aq) + C₂H₆O (aq)

C’est une réaction totale et lente à température ambiante.

1.  Suivi cinétique en utilisant la variation au cours du temps de la conductivité du mélange réactionnel.

-  Quantité de matière des différents réactifs :

-  Quantité de matière initiale d’éthanoate d’éthyle :

-   

-  Quantité de matière initiale d’ions hydroxyde :

-  n₀ = C₀ × V₀

-  n₀ = 2,5 × 10^–2 × 20,0 × 10^–3

-  n₀ = 5,0 × 10^–4 mol

-  Tableau d’avancement de la réaction :

-  On ne fait pas apparaître les ions sodium Na⁺ (aq) dans le tableau d'avancement

-  Les différentes espèces chargées présentes dans le mélange réactionnel :

-  L’ion sodium Na⁺ (aq) et l’ion hydroxyde HO^– (aq),

-  Et ion éthanoate C₂H₃O₂^– (aq) ou CH₃ – COO^– (aq)

-  Volume du mélange réactionnel :

-  On néglige le volume d’éthanoate d’éthyle pur devant le volume d’eau distillée et le volume de soude versée :

-  V = V₀ + V_eau

-  V ≈ 100 mL

-  Cela revient à négliger un volume de 2,0 mL devant un volume de 100 mL.

-  Concentration des différentes espèces chargées à l’instant t :

-  Concentration des ions sodium Na⁺ (aq) :

-   

-  La concentration des ions sodium Na⁺ (aq) ne varie pas au cours de la réaction.

-  [Na⁺] = C_i = 5,0 × 10^–3 mol . L^–1

-  Concentration des ions hydroxyde HO^– (aq)

-   

-  Au cours de la réaction, la concentration en ions hydroxyde HO^– (aq) diminue.

-  Concentration en ion éthanoate C₂H₃O₂^– (aq) :

-   

-  Au cours de la réaction la concentration en ions éthanoate C₂H₃O₂^– (aq) augmente.

-  Évolution de la conductivité de la solution au cours de la réaction :

-  La conductivité σ de la solution est égale à la somme des conductivités due aux cations et aux anions.

-  On écrit :

-   σ = σ (+) + σ (–)

-  Formule générale :

-   

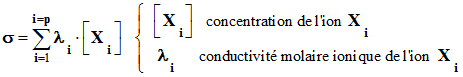
-  La conductivité σ d’une solution ionique dépend de la nature des ions présents X_i et de leur concentration [ X_i ] respectives.

-  Dans le cas présent :

-  σ = λ (HO^–) . [ HO^– ] + λ (Na⁺) . [ Na⁺ ] + λ (C₂H₃O₂^–) . [C₂H₃O₂^– ]

-  Au cours de la réaction, les ions hydroxyde HO^– (aq) disparaissent.

-  Ils sont remplacés par les ions éthanoate C₂H₃O₂^– (aq).

-  En conséquence, la concentration en ions hydroxyde HO^– (aq) diminue.

-  La concentration en ions éthanoate C₂H₃O₂^– (aq) augmente

-  Et la concentration en ions sodium Na⁺ (aq) ne varie pas.

-  En résumé :

-  Lorsqu’un ion hydroxyde HO^– est consommé, un ion éthanoate C₂H₃O₂^– est formé.

-  Les ions sodium Na⁺ ne participent pas à la réaction, ils ne jouent aucun rôle sur la variation de la conductivité du mélange réactionnel.

-  Tout se passe comme si on remplaçait un ion hydroxyde HO^– par un ion éthanoate C₂H₃O₂^–

-  Comme λ (HO^–) > λ (C₂H₃O₂^–) la conductivité globale de la solution diminue au cours du temps.

-  λ (C₂H₃O₂^–) = 4,09 × 10^–3 S . m² . mol^–1 ;

-  λ (HO^–) = 19,9 × 10^–3 S . m² . mol^–1 

-  On peut suivre l’évolution de l’avancement de la réaction à partir de la mesure de la conductivité de la solution :

-   

-  Le suivi cinétique de cette réaction chimique est possible grâce à l’utilisation d’un conductimètre.

2.  Protocole expérimental détaillé permettant d’effectuer le suivi cinétique.

-  Mélange d’un volume :

-  V₀ = 20,0 mL). d’hydroxyde de sodium de concentration C₀,

-  Eau distillée :

-  V_eau = 80 mL

-  Volume d’éthanoate d’éthyle pur :

-  V₁ = 2,0 mL (en excès)

   Verser environ 50 mL de solution d’hydroxyde de sodium dans un bécher de 100 mL

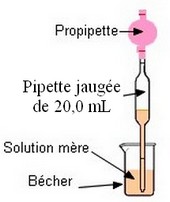
-  Prélever 20,0 mL de la solution d’hydroxyde de sodium de concentration C₀ à l’aide d’une pipette jaugée de 20,0 mL munie de sa propipette.

-  Introduire ce volume dans un bécher de 200 mL.

-  Prélever environ 80 mL d’eau distillée.

-  Les ajouter dans le bécher précédent.

  Dans le bécher :

-  Plonger un barreau aimanté

-  Positionner le bécher sur un agitateur magnétique.

  Cellule conductimétrique :

-  Positionner la cellule conductimétrique.

-  Elle doit être bien immergée et ne pas être en contact avec le barreau aimanté.

-  Mettre en marche l’agitateur magnétique.

-  Effectuer le réglage pour obtenir une agitation douce.

-  Le conductimètre, relié à l’interface d’un ordinateur, permet le suivi de la conductivité du mélange réactionnel au cours du temps t,

ceci grâce à une application adaptée.

-  La température de la solution reste égale à 25 ° C.

  Les mesures :

-  Prélever 2 mL d’éthanoate d’éthyle pur à l’aide de la pipette graduée munie de sa propipette

-  Les introduire rapidement dans le bécher et déclencher l’enregistrement.

-  L’application, utilisée par l’ordinateur, permet de relever la valeur de la conductivité du mélange réactionnel à intervalles de temps t réguliers.

-  Les mesures :

-  À l’instant initial : t = t₀

-  On verse les 2,0 mL d’éthanoate de sodium :

-  L’avancement de la réaction x = 0 et σ = σ₀

-  Expression de σ₀ à l’instant initial :

-  σ₀ = λ (HO^–) . [ HO^– ]₀ + λ (Na⁺) . [ Na⁺ ]₀

-  σ₀ = (λ (HO^–)+ λ (Na⁺)) . C_i

-  À l‘instant t :

-  σ (t)= λ (HO^–) . [ HO^– ]_t + λ (Na⁺) . [ Na⁺ ]_t + λ (C₂H₃O₂^–) . [C₂H₃O₂^– ]_t

-   

-  Or :

-  [ Na⁺ ]₀ = [ Na⁺ ]_t = C_i

-   

-  En ordonnant :

-   

-  Comme la réaction est totale,

-  La valeur de l’avancement x augmente au cours du temps :

-  0 ≤ x ≤ n₀ ≈ 0,50 mmol

-  Dans l’état initial

-  x = 0 et σ (0) = σ₀

-  Dans l’état final :

-  x = x_max = n₀ ≈ 0,50 mmol

-   

-  Or :

-  Initialement : S . m² . mol^–1

-  σ₀ = (λ (HO^–)+ λ (Na⁺)) . C_i

-  σ₀ = (19,9 × 10^–3 + 5,01 × 10^–3) × 10^–3 × 5,0 × 10^–4

-  σ₀ ≈ 1,1455 × 10^–8 S

-  σ₀ ≈ 1,15 × 10^–8 S

-  Finalement :

-  σ (f) = (λ (C₂H₃O₂^–) + λ (Na⁺)) . C_i

-  σ (f) = (4,09 × 10^–3 + 5,01 × 10^–3) × 10^–3 × 5,0 × 10^–4

-  σ (f) ≈ 4,55 × 10^–9 S

-  Ainsi la conductivité diminue bien au cours du temps t.

►  Étude cinétique :

-  Vitesse d’apparition d'un produit P :

-  La vitesse v_a (P)_t d’apparition, d’un produit P, est égale à la dérivée par rapport au temps de sa quantité de matière n_P :

-   

-  Dans le cas qui nous intéresse :

-   

-  Or à chaque instant, n (C₂H₃O₂^–) = x

-   

-  Comme le volume du mélange réactionnel est constant au cours de la réaction :

-  n (C₂H₃O₂^–) = x = [C₂H₃O₂^–] . V

-   

-  La vitesse volumique d’apparition de l’ion éthanoate à la t est définie par la relation suivante :

-   

►  Vitesse volumique d’apparition d’un produit P :

-  La vitesse volumique d’apparition, de l’ion éthanoate v_app (C₂H₃O₂^–)_t, est égale à la dérivée par rapport au temps de sa concentration :

-   

-  La vitesse d’apparition de l’ion éthanoate v_a (C₂H₃O₂^–)_t, est égale à la dérivée par rapport au temps de l’avancement x de la réaction :

-   

-  Comme le volume V est constant, la vitesse volumique v_app (C₂H₃O₂^–) est proportionnelle à .

-  Or graphiquement, le terme  représente le coefficient directeur de la tangente à la courge x = f (t).

-  Ce terme diminue au cours du temps, car les tangentes sont de moins en moins pentues.

-  La vitesse volumique diminue au cours du temps et s’annule lorsque la réaction est terminée (tangente horizontale).

-  Graphe

►  Le temps de demi-réaction :

-  Le temps de demi-réaction est la durée au bout de laquelle l’avancement x atteint la moitié de sa valeur finale :

-  Dans le cas présent : x_f = x_max = 500 μmol.

-   

-  Exploitation graphique :

-  On trace la droite x (t_1/2) = 250 μmol.

-  Cette droite coupe le graphe x = f (t) en un point dont l’abscisse est t_1/2.

-  t_1/2 ≈ 1,6 min

-  Le temps de demi-réaction t_1/2 permet d’évaluer la durée nécessaire à l’achèvement de la transformation chimique étudiée.

-  L’expérience montre qu’un système siège d’une réaction caractérisée par le temps de réaction t_1/2 cesse pratiquement d’évoluer

au bout d’une durée de l’ordre de quelques t_1/2 (4 à 7 suivant la précision recherchée).

►  Loi des vitesse d’ordre 1 :

-  Réaction étudiée :

C₄H₈O₂ (ℓ) + HO^– (aq) → C₂H₃O₂^– (aq) + C₂H₆O (aq)

-  L’espèce chimique C₄H₈O₂ (ℓ)  a été introduite en large excès :

-  Pour montrer que la réaction est d’ordre 1 par rapport à l’ion hydroxyde,

-  Il faut vérifier que les vitesses volumiques de disparition des réactifs ou d’apparition des produits sont proportionnelles

à la concentration [HO^–]_t de l’espèce HO^– (aq) au cours du temps.

-  C’est -à-dire :

-   

-  Étude avec le tableur Excel :

-  Il faut calculer

-  Dans la cellule H5, on tape la formule suivante :

-  (F5 – F4) / (B5 – B4) / 0,1 / 1000

-  On obtient ainsi la valeur en mmol / L / min

-  On recopie vers le bas autant que nécessaire.

-  Graphe :

-  Les points sont sensiblement alignés.

-  La droite moyenne passe par l’origine.

-  La vitesse d’apparition de l’ion éthanoate est proportionnelle à la concentration en ions hydroxyde.

-   

-  On peut faire un traitement statistique grâce au tableur Excel :

-  Les différentes sélections :

-  Mise en forme de la courbe :

-  Le tableur Excel affiche l’équation de la droite et le coefficient de détermination R².

-  Équation : y = 0,4797 x – 6 × 10^–16

-  En donnant le résultat avec 3 chiffres significatifs :

-  y ≈ 0,480 x

-  Traduction :

-  v_app (C₂H₃O₂^–)_t (mmol . L^–1 . min^–1) ≈ 0,480 × [HO^–]_t (mmol . L^–1)

-  La constante k₂ :

-  k₂ = 0,480 min^–1

-  Type de réaction chimique :

-  La relation est du type :

-  v_app (C₂H₃O₂^–)_t = k₂ × [HO^–]_t

-  En conclusion :

-  La réaction est d’ordre 1 par rapport aux ions hydroxyde HO^– (aq).

-  La vitesse d’apparition des ions éthanoate C₂H₃O₂^– (aq) est proportionnelle à la concentration des ions hydroxyde HO^– (aq).