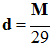Dans le cadre d’un projet pluridisciplinaire sur le thème de la spéléologie,

 des élèves de terminale doivent faire l’exploration d’une grotte où

ils risquent de rencontrer des nappes de dioxyde de carbone CO₂. 

A teneur élevée, ce gaz peut entraîner des évanouissements et même la mort. 

Le dioxyde de carbone est formé par action des eaux de ruissellement acides

 sur le carbonate de calcium CaCO₃ présent dans les roches calcaires. 

Le professeur de chimie leur propose d’étudier cette réaction.

La réaction chimique étudiée peut être modélisée par l’équation :

CaCO_3(s)  +  2 H₃O⁺_(aq)   =   Ca²⁺_(aq)  +  CO_{2 (g)}  +  3 H₂O _(l)

1. Calculer la densité par rapport à l’air du dioxyde de carbone CO_{2 (g)}. 

Dans quelles parties de la grotte ce gaz est-il susceptible de s’accumuler ?

2.  Déterminer les quantités de matière initiale de chacun des réactifs.

3. Dresser le tableau d’avancement de la réaction. En déduire la valeur x_max de l’avancement maximum. 

Quel est le réactif limitant ?

4. Relations :

a)- Exprimer l’avancement x de la réaction à une date t en fonction de V (CO₂), T, P_atm et R.

b)- Calculer sa valeur numérique à la date t = 20 s.

c)- Calculer le volume maximum de gaz susceptible d’être recueilli dans lesconditions de l’expérience. 

La transformation est-elle totale ?

5. Les élèves ont calculé les valeurs de l’avancement x et reporté les résultatssur le graphe donné en annexe (à rendre avec la copie).

a)-  Donner l’expression de la vitesse volumique de réaction en fonction de l’avancement x et du volume V_S de solution. 

Comment varie la vitesse volumique au cours du temps ? Justifier à l’aide du graphe.

b)-  Définir le temps de demi-réaction t_1/2. 

Déterminer graphiquement sa valeur sur l’annexe.

6. La température de la grotte qui doit être explorée par les élèves est inférieure à 25°C.

a)- Quel est l’effet de cet abaissement de température sur la vitesse volumique de réaction à la date t = 0 s ?

b)- Tracer, sur l’annexe, l’allure de l’évolution de l’avancement en fonction du temps dans ce cas.

7. La réaction précédente peut être suivie en mesurant la conductivité σ de la solution en fonction du temps.

a)-  Faire l’inventaire des ions présents dans la solution. 

Quel est l’ion spectateur dont la concentration ne varie pas ?

b)-  On observe expérimentalement une diminution de la conductivité. 

Justifier sans calcul ce résultat connaissant les valeurs des conductivités molaires des ions à 25°C :

                        λ (H₃O⁺) = 35,0 mS.m ².mol ^–1

                        λ (Ca²⁺) = 12,0 mS.m ².mol ^–1

                        λ (Cl^–) = 7,5 mS.m ².mol ^–1

c)- Calculer la conductivité σ de la solution à l’instant de date t = 0 s.

d)- Montrer que la conductivité est reliée à l’avancement x par la relation : σ = 4,25 – 580 x

e)- Calculer la conductivité de la solution pour la valeur maximale de l’avancement.