|
DOC. N° 03 |
Notion de statistiques pour les sciences physiques |
|
|
|
-
On appelle x,
le caractère étudié.
-
On appelle xi la valeur numérique du caractère étudié.
-
L’effectif, noté
ni, est le nombre de mesures donnant le résultat xi.
-
La fréquence
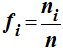 , ou n est le nombre
total de mesures :
, ou n est le nombre
total de mesures : ![]()
II-
Les paramètres de position.
1)-
La moyenne : moyenne pondérée, moyenne arithmétique.
-
On la note
![]()
-
Formule : ![]()
-
Cette moyenne est
le paramètre de position le plus couramment utilisé et le plus rapide à
calculer.
- C’est la valeur de
x qui correspond à l’effectif maximum.
- Il y a autant de mesures supérieures que de mesures inférieures à
cette valeur.
4)-
Les paramètres de dispersion.
a)-
L’écart moyen. (écart
arithmétique ou moyenne des écarts).
-
On peut calculer
l’écart absolu d’une mesure :
![]() et faire la moyenne
pondérée de ces écarts pour obtenir l’écart moyen que l’on note e.
et faire la moyenne
pondérée de ces écarts pour obtenir l’écart moyen que l’on note e.
-
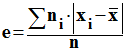
b)-
L’écart type. On utilise
surtout en statistique l’écart type ou l’écart quadratique moyen, noté σ.
-
Le calcul de
l’écart type découle de celui de la variance car l’écart type est égal à la
racine carrée de la variance.
-
![]()
-
La variance peut
se calculer à partir de la formule de Kœnig :
-
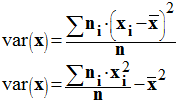
-
En conséquence : 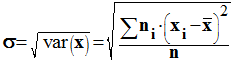
c)-
L’intervalle
interquartile.
-
Le premier
quartile Q1 : il y a 25 % de mesures inférieures.
-
Le troisième
quartile Q3 : il y a 25 % de mesures supérieures.
-
Le deuxième
quartile Q2 : c’est la médiane.
-
Il y a
50 % de mesures dans l’intervalle interquartile [Q1,
Q2].
-
Effectif total :
n = 100 ; Moyenne :
![]() ; e ≈
1,979 : σ ≈ 2,47 ;
; e ≈
1,979 : σ ≈ 2,47 ;
d)-
Remarque :
-
ces
trois paramètres de dispersion sont liés entre eux lorsque la distribution est
normale ou lorsque la distribution est pratiquement normale.
-
σ
≈ 1,25 e
-
Dans cet
exemple : σ ≈ 2,47 et σ ≈ 1,25 e
=>
σ ≈ 1,25 e
-
![]()
-
Dans cet
exemple : σ ≈ 2,47 ; ![]()
-
L’écart est
important car il est difficile de déterminer les valeurs des différents
quartiles.
-
On démontre en
statistique que la distribution des mesures, lorsque le nombre de mesures
augmente tend vers une distribution normale dite de Gauss – Laplace.
-
Le nombre de
mesures doit être supérieur à 50.
-
La Loi Normale :
-
On démontre en
probabilité que
-
Si
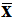 représente la moyenne, σ
l‘écart-type et
x une
valeur incluse dans l'ensemble de données, alors
représente la moyenne, σ
l‘écart-type et
x une
valeur incluse dans l'ensemble de données, alors
-
environ
68 % des données se situent à l'intérieur de l'intervalle :
![]() .
.
-
environ
95 % des données se situent à l'intérieur de l'intervalle :
![]() .
.
-
Environ 99 % des
données se situent à l'intérieur de l'intervalle :
![]() .
.
-
Dans le cas d’une
expérience de physique, on se heurte à des problèmes d’estimation.
-
Si l’on a une
série de n mesures d’une grandeur x (résistance, nombre
d’impulsions d’une source radioactive, …), on peut calculer :
-
La moyenne
![]() ,
,
-
L’écart type σ,
de cette série de mesures.
-
Mais la valeur de
la moyenne 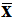 ne
représente qu’une estimation, une valeur approchée de la valeur réelle inconnue
notée x.
ne
représente qu’une estimation, une valeur approchée de la valeur réelle inconnue
notée x.
-
On démontre que
lorsque la distribution ressemble à une loi normale, la probabilité pour que
x appartienne à l’intervalle de confiance ;
![]() est supérieure à 99 %.
est supérieure à 99 %.
-
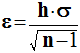 ; h est la constante de Student. Elle est donnée par les tables de
Student.
; h est la constante de Student. Elle est donnée par les tables de
Student.
-
La grandeur ɛ
est appelée incertitude, erreur standard ou écart probable.
|
n |
h à 99 % |
h à 95 % |
|
51 |
2,678 |
2,009 |
|
61 |
2,660 |
2,000 |
|
81 |
2,639 |
1,990 |
|
101 |
2,626 |
1,984 |
|
201 |
2,601 |
1,972 |
|
501 |
2,586 |
1,965 |
|
1001 |
2,576 |
1,960 |
-
Dans l’exemple
précédent : comme n = 100, h ≈ 2,626
-
Valeur de ɛ : 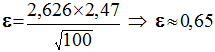
-
La probabilité
pour que x
Î ] 1000, 1002 [ est de 99 %.
-
La tension UPN
aux bornes d’un générateur qui débite dans un circuit
l’intensité I vérifie la loi théorique :
|
UPN
= E –
r .
I
{ |
E :
f.e.m en volt (V) |
|
r :
résistance interne en ohm (Ω) |
-
Les valeurs
expérimentales sont les suivantes :
|
I
en A |
0,15 |
0,26 |
0,38 |
0,52 |
0,72 |
0,92 |
1 |
|
U
en V |
3,82 |
3,59 |
3,33 |
3,10 |
2,77 |
2,41 |
2,19 |
-
En reportant les
valeurs sur du papier millimétré, on constate que les points expérimentaux sont
sensiblement alignés.
-
Pour que
l’expérience permette de déterminer les grandeurs E et r, il
faudrait connaître la droite qui s’ajuste le mieux aux données expérimentales.
-
On peut faire un
ajustement graphique par tâtonnement (On dit alors que l’on trace la droite
moyenne : méthode que l’on utilise en classe de seconde).
-
Une autre méthode
très utilisée, est la méthode des moindres carrés.
a)-
Méthode des
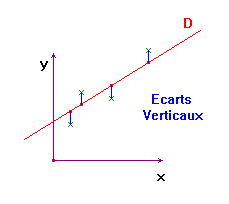
moindres carrés verticaux.
-
On cherche par le
calcul, la droite telle que la somme des carrés des distances verticales entre
les points et la droite soit minimale.
-
Exemple : On
possède n points expérimentaux (x 1 ; y 1),
(x 2 ; y 2), (x 3 ; y
3), ……(x n ; y n).
- Dans notre exemple, les points expérimentaux sont sensiblement alignés.
- On cherche une
droite D d’équation : y = a . x + b.
-
La droite D
est telle que la somme S des carrés des écarts verticaux est minimale :
-
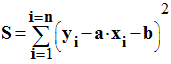 (1)
(1)
►
première
étape : supposons que la valeur de a
est fixée. En conséquence, la seule variable est
b.
-
S
est minimum si : 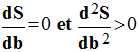 .
.
-
À l’aide de
l’expression (1), on peut calculer la dérivée première de S par rapport à
b :
-
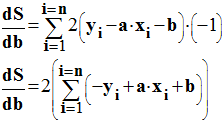
-
On peut calculer
la dérivée seconde :
-
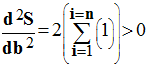
-
En conséquence : 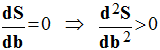
-
On est bien en
présence d’un minimum.
-
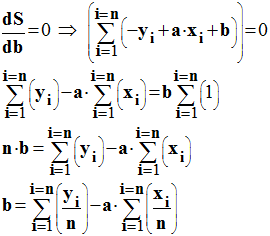
-
Or : 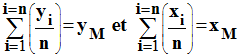
-
b
= yM – a . xM
-
Cela signifie
que, parmi toutes les droites de coefficient directeur donné a, celui qui
rend S minimum, est celle qui passe par le point moyen M de
coordonnées (x M ; y M).
► Deuxième étape :
On fait le changement de variable suivant :
-
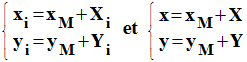
-
On se limite aux
droites passant par le point M. Ces droites ont pour équation :
-
Y
= a . X.
-
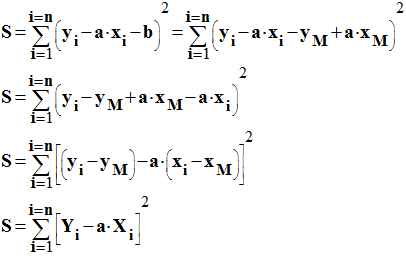
-
S
est minimum par rapport à la variable a si
 .
.
-
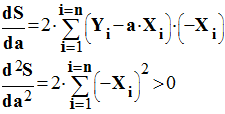
-
On est bien en
présence d’un minimum.
-
Détermination de
l’expression de a :
-
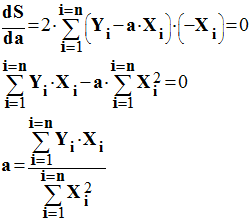
-
Expression qui
permet le calcul de la valeur de a :
-
Or : 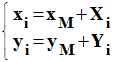
-
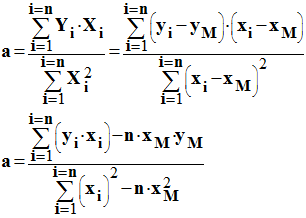
-
à
partir de la valeur de a, on peut en déduire celle de b grâce à
l’expression :
-
b
= yM – a . xM
-
La droite obtenue
d’équation : y = a . x + b est appelée droite de
régression de y en x.
b)- Méthode
des moindres carrés horizontaux.
-
On cherche par le
calcul, la droite telle que la somme des carrés des distances horizontales entre
les points et la droite soit minimale.
-
Exemple : On
possède n points expérimentaux (x 1 ; y 1),
(x 2 ; y 2), (x 3 ; y
3), ……(x n ; y n).
- Dans notre exemple, les points expérimentaux sont sensiblement alignés.
- On cherche une
droite D’ d’équation : y = a’ . x + b’.
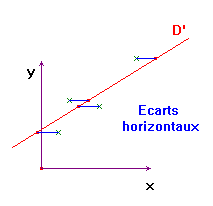
-
La droite D’
est telle que la somme S des carrés des écarts horizontaux est minimale :
-
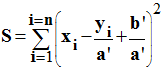 (1)
(1)
► première
étape : supposons que la valeur de a’
est fixée. En conséquence, la seule variable est
b’.
-
S
est minimum si
 .
.
-
À l’aide de
l’expression (1), on peut calculer la dérivée première de S par rapport à
b :
-

-
Puis la dérivée
seconde par rapport à b’.
-
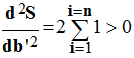 Il s’agit bien d’un
minimum.
Il s’agit bien d’un
minimum.
-
En conséquence,
S est minimum si
-
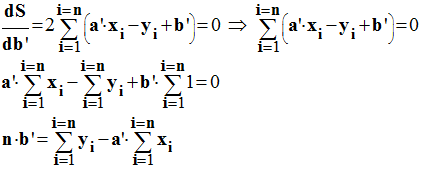
-
Or : 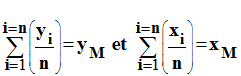
-
b’
= yM – a’ . xM
-
Cela signifie
que, parmi toutes les droites de coefficient directeur donné a’, celui
qui rend S minimum, est celle qui passe par le point moyen M de
coordonnées (xM ; yM).
► Deuxième étape :
On fait le changement de variable suivant :
-
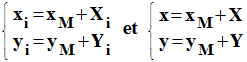
-
On se limite aux
droites passant par le point M. Ces droites ont pour équation :
-
Y
= a . X.
-
On remplace b’
par son expression dans S.
-
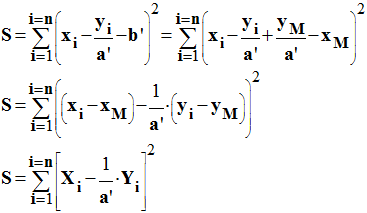
-
S
est minimum par rapport à la variable a’ si
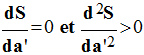 .
.
-
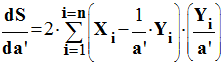
-
Détermination de
l’expression de a’ :
-

-
Expression qui
permet le calcul de la valeur de a’ :
-
Or : 
-
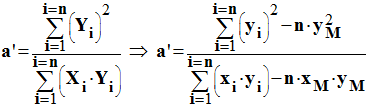
-
à
partir de la valeur de a’, on peut en déduire celle de b’ grâce à
l’expression : b’ = yM – a’ . xM
-
La droite obtenue
d’équation : y = a’ . x + b est appelée droite de
régression de x en y.
a)- Le coefficient de
corrélation.
-
Le coefficient de
corrélation linéaire r est défini par l’expression suivante : ![]()
-
Si | r | =
1 les deux droites D et D’ sont confondues. Tous les points du
nuage de points sont alignés. Il y a corrélation linéaire.
-
Si r = 0
il n’y a pas de corrélation linéaire.
-
Si | r | ≈
1 il y a dépendance linéaire statistique entre les variables x et y.
1)-
Caractéristique d’un générateur.
-
La tension UPN
aux bornes d’un générateur qui débite dans un circuit
l’intensité I vérifie la loi théorique :
|
UPN
= E –
r .
I
{ |
E :
f.e.m en volt (V) |
|
r :
résistance interne en ohm (Ω) |
a)-
Tableau de
valeurs.
|
I
en A |
0,15 |
0,26 |
0,38 |
0,52 |
0,72 |
0,92 |
1 |
|
U
en V |
3,82 |
3,59 |
3,33 |
3,10 |
2,77 |
2,41 |
2,19 |
b)-
Exploitation.
-
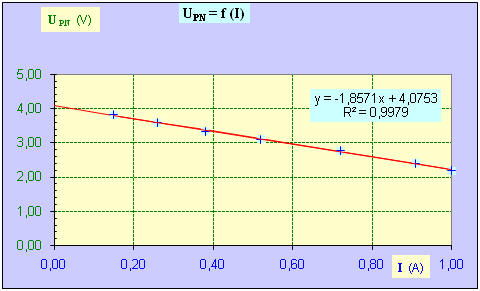
Graphe :
UPN
= f (I).
-
Une calculatrice
graphique ou un tableur permet de déterminer l’équation de la droite et de
donner le coefficient de corrélation et le coefficient de détermination.
-
Il faut
interpréter le résultat :
-
La force
électromotrice du générateur est donnée par la valeur de l’ordonnée à l’origine
E ≈ 4,08 V
-
La résistance
interne du générateur est donnée par la valeur absolue du coefficient directeur
de la droite D.
-
r
≈ 1,86 Ω.
-
Le coefficient de
corrélation
![]() .
.
-
Il y a une
dépendance linéaire entre les grandeurs UPN et I.
-
Le résultat est
en adéquation avec le modèle choisi :
-
UPN
= -1,86 I + 4,08.
2)-
Exemple d’ajustement se ramenant à un ajustement affine.
► Dans une
substance radioactive, si N0
désigne le nombre de noyaux radioactifs au temps 0, le nombre
N d’atomes radioactifs présents au
temps t est donné par la relation :
-
N
= N0 . e
– λ.t.
-
À partir de
l’indium radioactif, on a obtenu les résultats suivants :
|
t
en min |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|
N |
98 |
92 |
87 |
80 |
73 |
70 |
67 |
63 |
60 |
-
On peut donner
une autre formulation de la loi théorique pour ramener notre étude à celle d’une
fonction affine.
-
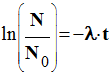
-
On détermine la
valeur de λ à l’aide d’un ajustement linéaire à partir des valeurs de
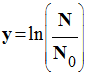 et de x =
t.
et de x =
t.
-
On calcule la
droite de régression de y par rapport à x.
|
t
en min |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
|
N |
98 |
92 |
87 |
80 |
73 |
70 |
67 |
63 |
60 |
|
|
0 |
-0.0632 |
-0.1196 |
-0.2029 |
-0.2945 |
-0.3365 |
-0.3803 |
-0.4418 |
-0.4906 |
-
Représentation
graphique et exploitation.
-
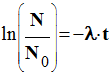 avec λ ≈ 0,0125 min –
1.
avec λ ≈ 0,0125 min –
1.
-
Comme on s’est
ramené à un ajustement affine en utilisant une fonction logarithmique, on dit
que l’on a procédé à un ajustement logarithmique.
-
On peut retrouver
la durée de demi-vie :
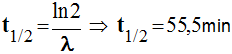 .
.