|
1.
Écrire
l’équation de la réaction :
Couples oxydant /réducteur : N2O5
/ NO2 et O2 / H2O
|
N2O5
|
+ 2 H+
|
+ 2 e–
|
=
|
2 NO2
|
+ H2O
|
|
× (2)
|
|
2 H2O
|
|
|
=
|
4 H+
|
+ 4 e–
|
+ O2
|
× (1)
|
|
2 N2O5
|
|
|
→
|
4 NO2
|
|
+ O2
|
|
2.
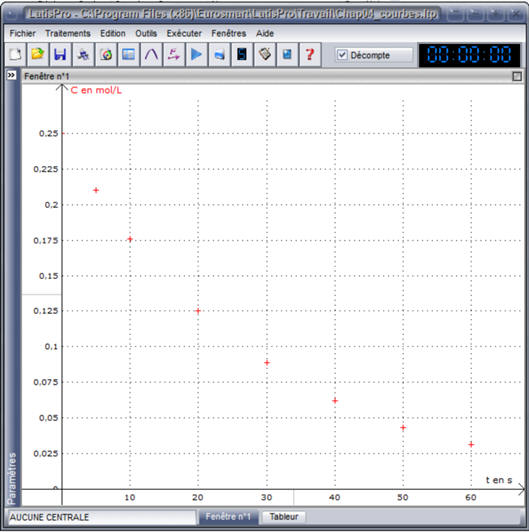
Tracer
la courbe C = f (t).
-
Exploitation réalisée avec le logiciel
Latis-Pro.
3.
À
l’aide de la courbe C = f (t) démontrer que la concentration en
pentaoxyde de diazote N2O5 suit une loi de vitesse
d’ordre 1.
►
Méthode 3 :
-
Il faut vérifier que l’évolution de la
concentration C de l’espèce
N2O5 au cours du temps obéit à une loi exponentielle du
type :
- C =
C0 . exp (-
k . t )
-
C
= C0 .
e
- k . t
- On réalise un traitement des mesures réalisées.
-
Traitement → Modélisation (choisir la
courbe à modéliser)
- Choisir le modèle : fonction exponentielle du type : A . exp(–
(X–Δ)/τ)+ v0
- Glisser la courbe à modéliser dans l'espace ''Courbe à
modéliser''
-
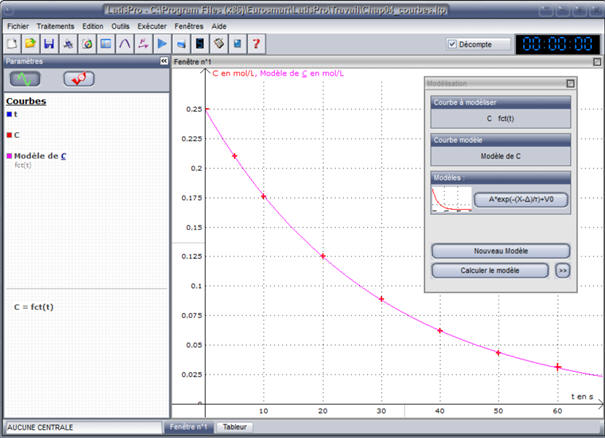
Sélectionner le modèle le mieux adapté.
- Puis cliquer sur calculer le modèle : la
courbe s’affiche.
-
Cliquer sur
 pour afficher le résultat de la
modélisation : pour afficher le résultat de la
modélisation :
-
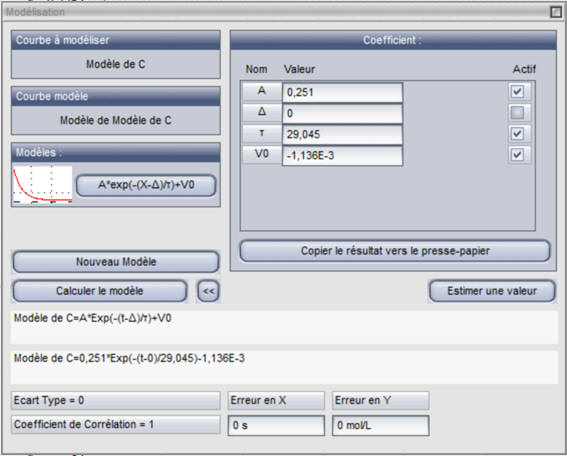
Exploitation des résultats :
- Le coefficient de corrélation
R = 1.
-
Les valeurs expérimentales sont en accord
avec le modèle choisi.
-
En considérant que
V0 <<
A, on peut écrire la
relation suivante :
- C ≈ 0,251 × exp (– t / 29,045)
-
Autre formulation :
-
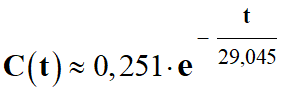
-
En en déduit les valeurs de
C0 et de k :
-
C =
C0 . e
-
k . t
-
En identifiant :
- C0 = 0,250 mol
. L–1 ≈ 0,251 mol . L–1
-
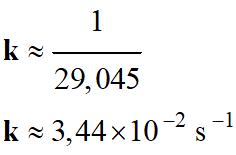
D’après les valeurs expérimentales, la concentration en pentaoxyde
de diazote N2O5
suit une loi de vitesse d’ordre 1.
4.
Tracer
la courbe ln (C) = g (t). Quelles sont les caractéristiques de la courbe
obtenue ?
-
Exploitation des mesures expérimentale
avec Latis-Pro.
- On crée une nouvelle variable : ln (C)
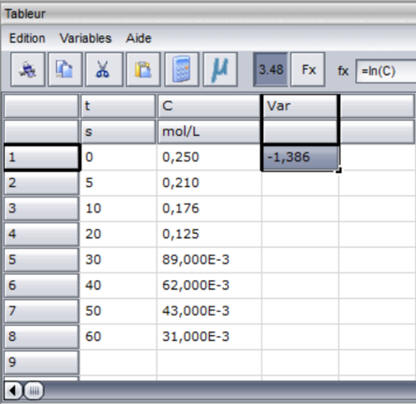
-
On recopie la formule vers le bas autant
que nécessaire.
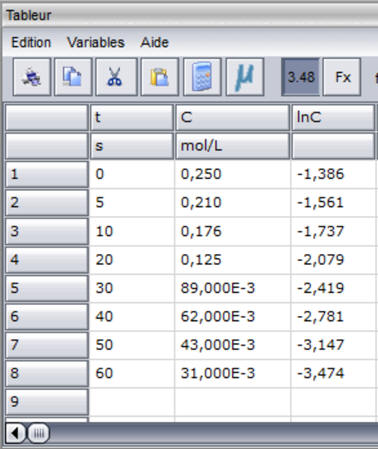
-
On peut maintenant représenter la
fonction : ln (C) ) =
g (t)
dans une nouvelle fenêtre.
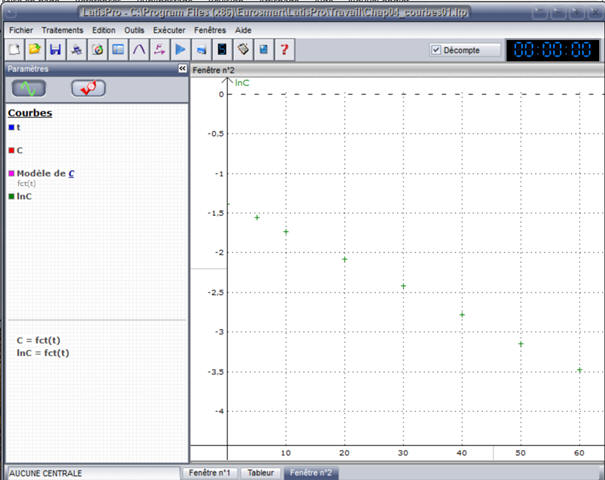
-
Les points sont sensiblement alignés.
- On réalise un traitement des mesures réalisées.
-
Traitement → Modélisation (choisir la
courbe à modéliser)
- Choisir le modèle : fonction affine
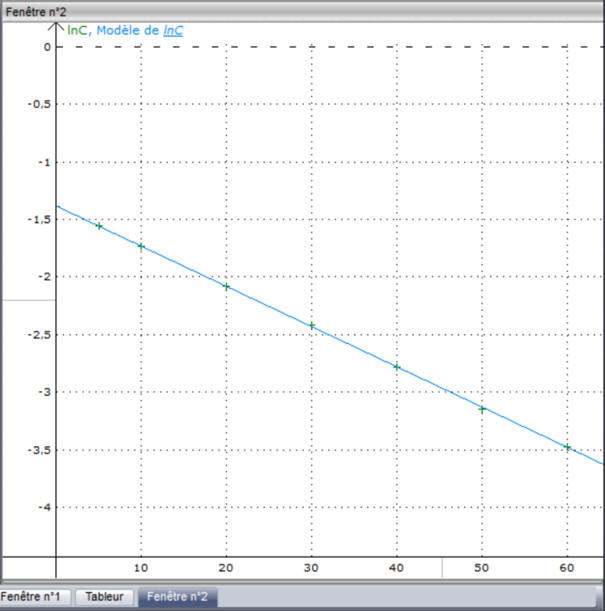
-
Puis cliquer sur calculer le modèle : la
courbe s’affiche.
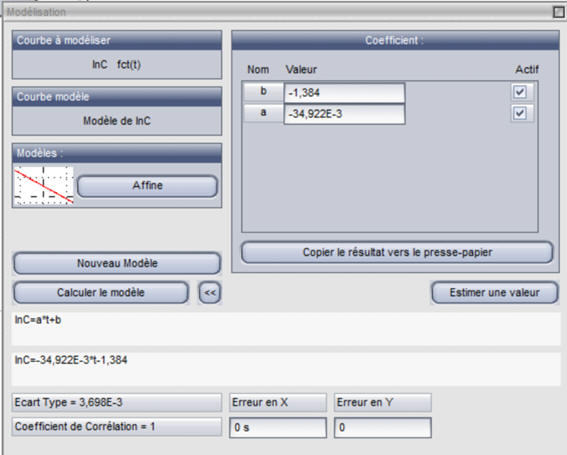
-
Cliquer sur
pour afficher le résultat de la
modélisation
-
Caractéristiques de la courbe obtenue :
- ln (C) = a . t + b
avec a ≈ – 34,922 × 10-3 s–1 et b ≈
– 1,384
-
On peut arrondir :
- a ≈ – 34,9 × 10–3 s–1 et b ≈ –
1,38
5.
Calculer la constante de la vitesse k à l’aide de la courbe ln (C) et en
déduire le temps de demi-réaction t1/2.
-
Exploitation :
- La réaction est d’ordre 1 :
-
Le pentaoxyde de diazote
N2O5
est un réactif, il disparait au cours de la réaction :
- vdisp = k .C
-
La grandeur k représente la
constante de vitesse.
- D’autre part :
-
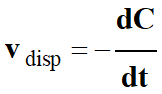
- En combinant des deux relations, on peut écrire que :
-
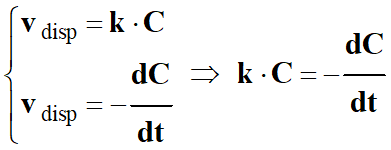
- En ordonnant, on obtient la relation suivante :
-
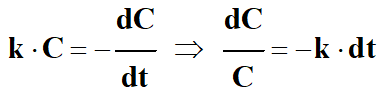
- Par intégration de la relation suivante, on obtient :
-
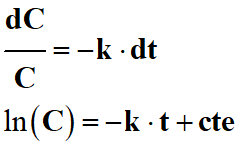
- Cette constante est liée aux conditions initiales
-
cte = ln (C0)
-
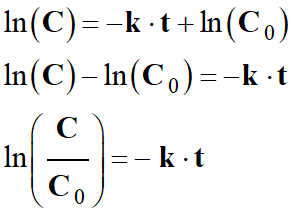
-
De l’exploitation de la courbe, on
détermine la valeur de k :
- k = – a ≈ 34,9 × 10–3 s–1
-
La valeur trouvée pour
k est bien en accord avec la valeur précédente :
- k ≈ 3,44
× 10–2 s–1
-
Incertitude relative :
-
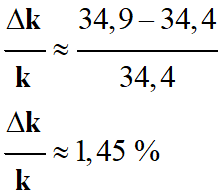
-
On peut vérifier la valeur de la
concentration initiale C0
du pentaoxyde de diazote N2O5.
- ln (C0) =
b ≈ – 1,38 =>
C0 = exp (b)
-
C0
≈ exp (– 1,38)
C0 ≈ 0,251 mol
. L–1 ≈ 0,250 mol . L–1
-
La valeur trouvée est bien en accord avec
la valeur expérimentale.
- Temps de demi-réaction :
-
Le temps de demi-réaction t1/2
d’un système chimique est la durée au bout de laquelle la moitié du
réactif limitant a été consommé.
- Dans le cas d’une réaction d’ordre 1 par rapport à un réactif :
-
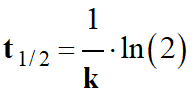
- Application numérique :
-
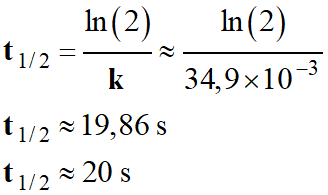
►
Une autre méthode pour déterminer la
valeur du temps de demi-réaction t1/2.
-
On utilise la courbe ln (C) = f (t) :
- Au temps t = 0,
C0 = 0,250 mol . L–1
-
Au temps
t =
t1/2, C =
C0 / 2 = 0,125 mol
. L–1
- L’abscisse du point de la courbe d’ordonnée
t1/2, donne la
valeur du temps de demi-réaction
t1/2.
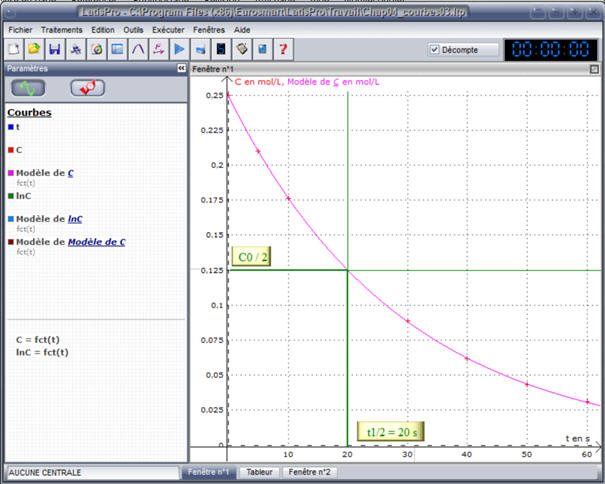
-
L’exploitation graphique donne :
t1/2 ≈ 20 s.
- Les deux résultats sont cohérents.
6.
Déterminer la valeur de la vitesse de réaction t = 0,10, 20, 30, 40, 50,
60 à l’aide du logiciel Latis-Pro.
►
Vitesse volumique de disparition d’un
réactif N2O5 :
-
La vitesse
vdisp
de disparition, du réactif
N2O5,
est égale à l’opposé de la dérivée par rapport au temps de sa
concentration :
-
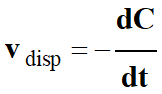
-
Graphiquement
:
- Cette vitesse est numériquement égale à la valeur du coefficient
directeur de la tangente T à la courbe C = f
(t)
- au point M d'abscisse t = 0,10, 20, 30, 40, 50,
60.
-
À l’aide du logiciel
Latis-Pro , on trace
la tangente à la courbe C = f
(t) pour les
différentes valeurs de t.
-
À l’aide du logiciel Latis-Pro , on trace
la tangente à la courbe C = f
(t)
pour les différentes valeurs de t.
- Faire un clic droit sur la fenêtre qui représente la courbe :
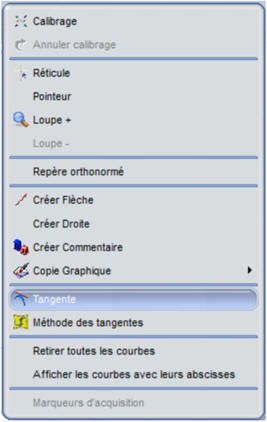
-
Sélectionner « Tangente » : puis tracer
les tangentes sur les différents points de la courbe.
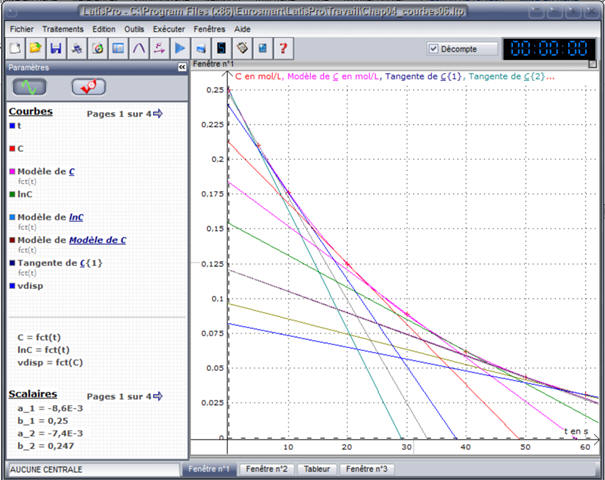
-
Relever les
différentes valeurs du coefficient directeur de chaque tangente tracée.
-
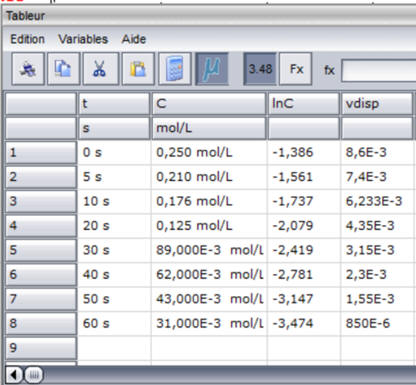
Tableau de valeurs : unité de
vdisp : mol . L–1
. s–1
-
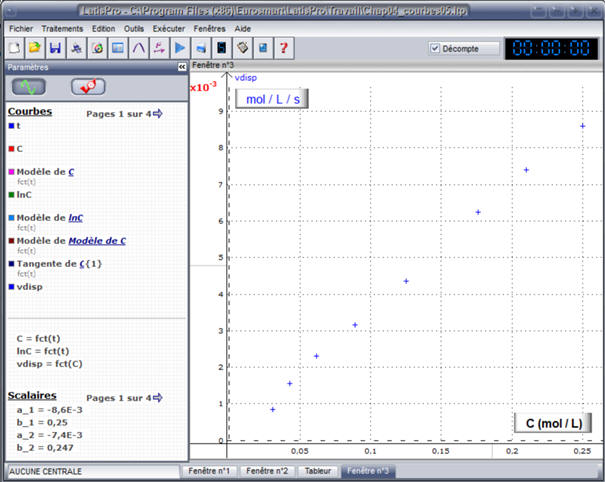
Courbe
vdisp =
h (C) :
-
Les points sont sensiblement alignés.
- La droite moyenne passe par l’origine.
-
On réalise un traitement des mesures
réalisées.
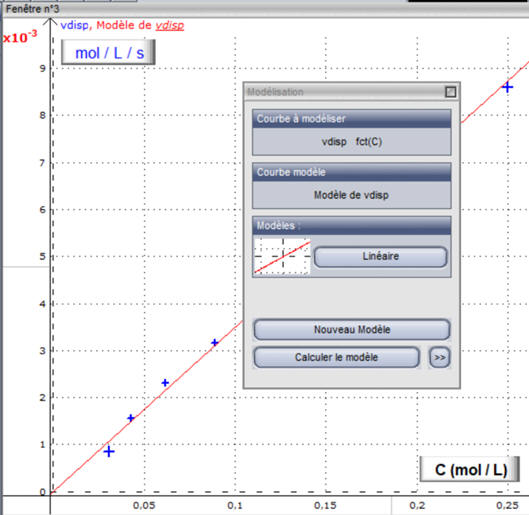
- Traitement → Modélisation (choisir la courbe à modéliser)
-
Choisir le modèle : fonction linéaire.
-
Cliquer sur
pour afficher le résultat de la
modélisation :
-
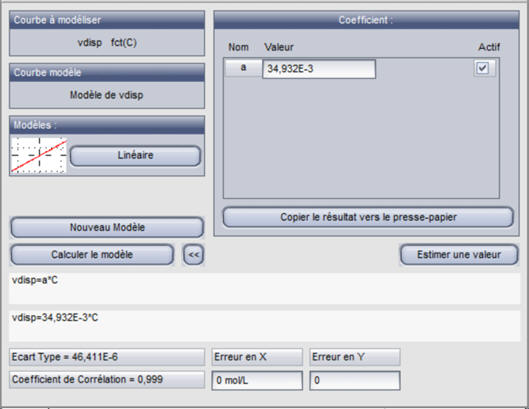
Le coefficient de corrélation
R = 0,999 ≈ 1.
- Le modèle choisi est en adéquation avec les valeurs numériques.
-
vdisp =
a . C
- La vitesse de disparition vdisp du réactif
N2O5
est proportionnelle à sa concentration
C.
-
Avec
a ≈ 34,932 × 10–3
s–1
- On peut arrondir cette valeur :
-
a
≈ 34,9 × 10–3 s–1
- On est bien en présence d’une réaction d’ordre 1 :
-
vdisp =
k . C
- avec k =
a
-
La grandeur
k représente la constante de
la vitesse :
- On retrouve la valeur de k :
-
k
≈ 34,9 × 10–3 s–1
- Cette valeur est en accord avec celle trouvée précédemment.
|