|
|
|
|
IV- Champ
magnétique Uniforme. |
|
DS |
|
DS 1)- Exercice 9 page 54 :
2)- Exercice 10 page 54 :
3)- Exercice 13 page 55 :
4)- Exercice 16 page 55 :
5)- Exercice 25 page 57 : 6)- Exercice 29 page 58 : Boussole des tangentes. |
I-
Interaction électromagnétique.
- Les aimants sont des corps capables d’attirer le fer.
- Cette propriété, appelée ferromagnétisme existe pour 5 éléments : le fer, le cobalt, le manganèse, le gadolinium et le dysprosium.
- Elle existe aussi pour certains alliages de ces métaux.
-
On nomme pôles
magnétiques les régions de l’aimant où le magnétisme semble être le plus
intense.
-
Par convention,
on désigne par pôle Nord l’extrémité d’une aiguille aimantée qui désigne le Nord
géographique et par pôle Sud l’autre extrémité.

-
Interaction entre
aimants : 2 pôles de même nom se repoussent et 2 pôles de nom différent
s’attirent.
2)- Analogie courant - aimant.
- Expérience d’Oersted : un conducteur parcouru par un courant engendre une interaction électromagnétique avec un aimant.
- Il crée dans tout l’espace environnant un
champ magnétique.
-
Faces d’une
bobine :
-
Une bobine est
constituée d’un enroulement de fil conducteur, recouvert d’un vernis isolant,
sur un cylindre de rayon r.
-
On désigne par L
la longueur de l’enroulement et par r le rayon d’une spire :

-
Si L est petit
devant r, la bobine est plate
-
Si L est voisin
de r la bobine est appelée : solénoïde
-
Si L est plus
grand que 10 r, le solénoïde est dit infini.
-
Une bobine
parcourue par un courant se comporte comme un aimant, elle possède une face Nord
et une face Sud.
-
Règles pour
déterminer les faces Nord et Sud d’une bobine :
-
Vue de face :

-
Vue de profil :
règle de la main droite

-
Un aimant ou un
conducteur parcouru par un courant agit à distance sur tout autre aimant.
-
Il modifie les
propriétés de l’espace qui l’environne. On dit qu’il produit un champ
magnétique.
- Pour détecter ce champ magnétique, on utilise le plus souvent une aiguille aimantée.
- Cette aiguille détectrice subit un couple de forces qui l’oriente.
- Elle donne
l’orientation du champ magnétique.
-
Représentation du
champ magnétique :
-
En un point
P
de l’espace, le champ magnétique est représenté par un vecteur :
|
|
- Le point
d’application P |
|
- La direction : celle de l’aiguille aimantée placée en ce point |
|
|
- Le sens dirigé du pôle Sud vers le pôle Nord de l’aiguille détectrice ou du pôle Nord vers le pôle Sud de la source de champ. |
|
|
- Valeur
B en tesla (T) |
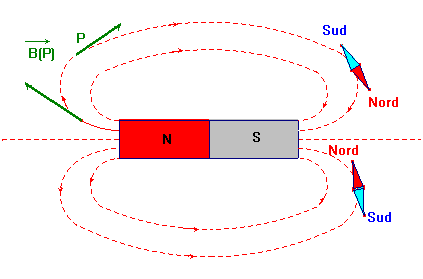
- Pour visualiser le spectre magnétique d’un aimant, on utilise de la limaille de fer.
- En présence de l’aimant, les grains de limaille de fer se comportent comme autant d’aiguilles aimantées qui s’orientent sous l’action du champ magnétique.
- Elles s’orientent et dessinent des lignes, appelées lignes de champ.
- L’ensemble des
lignes de champ donne le spectre magnétique.

3)- Mesure du champ magnétique.
-
Pour mesurer un
champ magnétique, on utilise un teslamètre à sonde de Hall.
-
Cette sonde
délivre une tension proportionnelle à la valeur du champ magnétique. Cette
tension est amplifiée par un système électronique.
-
Dans le S.I.,
l’unité de champ magnétique est le Tesla, symbole T.
-
Récapitulatif :
|
|
Point
d’application : P |
|
Direction :
tangente à la ligne de champ au point considéré. |
|
|
Sens : du pôle
Sud vers le pôle Nord de l’aiguille détectrice. |
|
|
Valeur B en
Tesla T |
III-
Champ magnétique terrestre.
(courants électriques provoqués par
les courants de convection dans le noyau ; fluide conducteur, principalement du
fer en fusion).
-
En un point
déterminé de la surface de la terre, le vecteur champ magnétique terrestre
![]() a les caractéristiques suivantes :
a les caractéristiques suivantes :
-
Il est contenu
dans un plan vertical, passant par les pôles magnétiques terrestres, appelé :
Plan méridien magnétique.
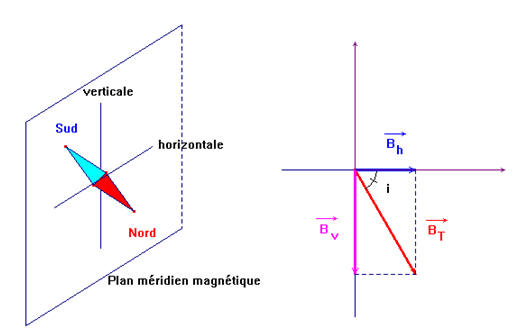
-
Son pôle Nord
s’incline vers le sol. Sa direction fait avec l’horizontale un angle i appelé
inclinaison (en France, i ≈ 60 °)
-
Ce champ
![]() peut être décomposé en
peut être décomposé en
|
Une composante horizontale
|
|
|
Et une composante verticale |
|
-
Remarque :
l’aiguille aimantée d’une boussole disposée horizontalement n’est sensible qu’à
la composante horizontale
![]() du champ magnétique
du champ magnétique
![]() .
.
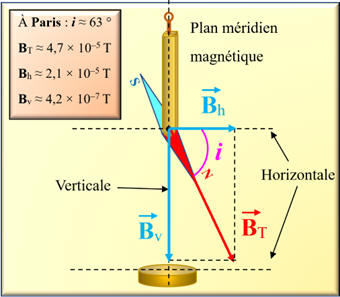
-
On peut mesurer la valeur de
Bh
grâce à la boussole des tangentes.
-
Bh
≈ 2,0
× 10
– 5
T
-
application :
Déterminer en un point O de la surface de la terre les valeurs de
Bv
et BT.
-
Schéma :


IV-
Champ magnétique Uniforme.
1)- Champ magnétique à l’intérieur d’un solénoïde.
(TP Physique N° 2)
- Le champ magnétique à l’intérieur d’un solénoïde est pratiquement uniforme.
- Les lignes de
champ à l’intérieur du solénoïde sont des droites parallèles.

-
Caractéristiques
du vecteur champ magnétique
![]() .
.
|
|
- point
d’application : le champ est uniforme |
|
- direction
parallèle à l’axe du solénoïde |
|
|
- sens : il
sort par le pôle Nord (règle de la main droite) |
|
|
- valeur :
|
|
|
Avec |
μ0 :
perméabilité du vide : - μ0 =
4 π
×
10 – 7 S.I (Henry / mètre : H / m)
- N :
nombre total de spires - ℓ : longueur
du solénoïde en mètre m -
- I
intensité du courant en ampère A - B valeur du champ magnétique en tesla T |
-
Remarques : La
perméabilité de l’air est voisine de celle du vide : μ =
μ0 .
μr
- Pour l’air : μr ≈ 1,0.
-
Pour le fer doux : μr = 1 +
χm avec μr perméabilité relative et
χm susceptibilité magnétique.
-
Ce sont deux
bobines : plates, coaxiales, séparées par la distance
ℓ et parcourues par
le courant I de même intensité et de même sens.
-
Si ℓ= r, le champ
magnétique est pratiquement uniforme entre les bobines.
-
Schéma :

-
Caractéristiques
de
![]() .
.
|
|
- point
d’application : le champ est uniforme |
|
- direction
parallèle à l’axe du solénoïde |
|
|
- sens : il
sort par le pôle Nord (règle de la main droite) |
|
|
- valeur :
|
- L’ensemble {bobine, noyau de fer doux} constitue un électroaimant.
- La valeur du champ magnétique créé par l’électroaimant varie toujours avec l’intensité du courant I,
mais la valeur du champ magnétique n’est plus proportionnelle
à l’intensité du courant I.
|
DS 1)- Exercice 9 page 54 :
2)- Exercice 10 page 54 :
3)- Exercice 13 page 55 :
4)- Exercice 16 page 55 :
5)- Exercice 25 page 57 : 6)- Exercice 29 page 58 : Boussole des tangentes. |