Champ de gravitation terrestre :

La valeur du champ de gravitation de la Terre à l’altitude

h est donnée par la relation :

1)- Avec quelle hypothèse cette formule est-elle été établie ?

2)- Pour h << R_T, donner une relation approchée de g (h)

En déduire la variation relative :  

3)- Calculer cette variation relative pour h = 4808 m, altitude du Mont-Blanc.

Donnée : R_T = 6380 km.

4)- Calculer la variation relative du poids d’un objet de masse m = 1 kg

Lorsqu’il passe du niveau de la mer au sommet du Mont-Blanc.

Champ de gravitation terrestre :

1)- Hypothèse :

On considère que la terre est un corps à répartition sphérique de masse.

2)- Hypothèse : h << R_T :

-     

-    Si h<<R_T,

3)- Variation relative h = 4808 m :

-     

4)- variation relative de poids :

-    

Champ de gravitation de la Lune

La Lune est considérée comme un corps à répartition sphérique de masse , de rayon R_L = 1740 km

et de masse M_L = 7,34 x 10²² kg.

1)- Donner l’expression du vecteur champ de gravitationde la Lune à une distance r ≥ R_L de son centre.

2)- a)- Calculer la valeur du champ de gravitation lunaire à la surface de la Lune.

b)- La comparer à la valeur du champ de gravitation terrestre g_0T à la surface de la Terre.

3)- Lors de la dernière mission lunaire (APOLLO XVII), les astronautes ont ramené 117 kg de roches.

Quel était le poids de ces roches :

a)- à la surface de la Lune ?

b)- à la surface de la Terre ?

Champ de gravitation de la Lune

La Lune est considérée comme un corps à répartition sphérique de masse , de rayon R_L = 1740 km

et de masse M_L = 7,34 x 10²² kg.

1)- Expression du vecteur champ de gravitation de la Lune (corps à répartition sphérique de masse et r > R_L).

2)- Champ de gravitation de la lune

a)- Valeur à la surface de la lune :

-   

b)-  comparaison avec celui de la terre :

-  

3)- Poids des roches.

a)-  À la surface de la lune.

-  P_L = m . g_0L ≈ 190 N

b)-  À la surface de la terre.

-  P_T = m . g_0T ≈ 1150 N  

La Terre, la Lune et le Soleil :

La distance entre la Terre et la Lune est de 384 000 kmen moyenne.

Le rapport des masses des deux planètes est :

1)- Entre la Terre et la Lune, il existe un point où le champ de gravitation de la Lune compense celui de la Terre.

Déterminer la position de ce point.

2)- Un satellite géostationnaire de 360 kg, à 42000 km du centre de la Terre, se trouve entre la Terre et la Lune.

Calculer le rapport des valeurs des forces de gravitations exercées par la Terre et la Lune  sur ce satellite.

3)- Le Soleil est à une distance moyenne :

D = 1,5 x 10¹¹ m de la Terre.

Calculer le rapport des valeurs des forces d’interaction

Gravitationnelle exercées par la Terre et le Soleil sur la Lune lorsque les trois astres sont alignés.

Donnée :

La Terre, la Lune et le Soleil :

La distance entre la Terre et la Lune est de 384 000 kmen moyenne.

Le rapport des masses des deux planètes est :

1)- Point ou le champ de gravitation de la terre compense celui de la lune.

2)- Rapport des forces de gravitation.

-  d = 384000 km ; r_a = 42000 km et r_b = 342000 km

3)- Soleil, Terre et Lune alignés.

-  d = 1,5 x 10¹¹ m ; r₁ = 3,84 x 10⁸ m ; r₂ = 1,496 x 10¹¹ m.

Variation de g avec l’altitude :

La variation de g avec l’altitude a pu être mise en évidence par Von Jolly au XIX^e siècle.  

Quatre ballons en verre identiques sont suspendus sous les plateaux d’une balance, comme l’indique le document ci-dessous.

Ces ballons sont fermés et deux entres eux sont pleins de mercure, les deux autres sont vides.

On établit l’équilibre lorsque les ballons pleins occupent les positions 1 et 4.

Puis ont permute les ballons 1 et 2, d’une part et 3 et 4 d’autre part.

On place alors la surcharge m dans le plateau B.

La distance entre les deux boules 1 et 2, 3 et 4 est d.

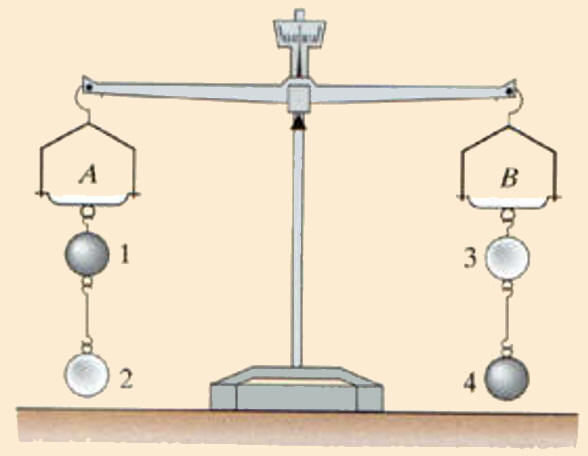
1)- Lorsque l’on passe de la position 1 à la position 2, g varie de Δg.

2)- Montrer que :

m . g = 2 M . Δg,

où M est la masse de mercure dans un ballon.

3)- Au cours d’une mesure, Von Jolly a trouvé :

M = 5 kg, d = 21 m et m = 63,4 mg.

Calculer .

4)- Comparer cette valeur à la valeur théorique

5)- Au cours de cette expérience, doit-on prendre en compte la poussée d’Archimède due à l’air ?

Variation de g avec l’altitude :

La variation de g avec l’altitude a pu être mise en évidence par Von Jolly au XIX^e siècle.  

Quatre ballons en verre identiques sont suspendus sous les plateaux d’une balance, comme l’indique le document ci-dessous.

Ces ballons sont fermés et deux entres eux sont pleins de mercure, les deux autres sont vides.

On établit l’équilibre lorsque les ballons pleins occupent les positions 1 et 4.

Puis ont permute les ballons 1 et 2, d’une part et 3 et 4 d’autre part.

On place alors la surcharge m dans le plateau B.

La distance entre les deux boules 1 et 2, 3 et 4 est d.

1)- Variation du poids du mercure entre les deux positions (1) et (2).

-  Du côté de A, l'altitude diminue de d en conséquence

-  P’_A = P_A + M . Δg, le poids augmente.

-    Du côté de B, l'altitude augmente de d en conséquence

-  P’_B = P_B – M . Δg, le poids diminue.

2)- L'équilibre est déplacé du côté de A et il faut rajouter la surcharge de masse m du côté de B.

-  En considérant que les bras des fléaux ont la même longueur ℓ,

à l'équilibre : 

-  P’_A . ℓ - P’_A . ℓ - P . ℓ = 0

-  P_A + M . Δg – P_B + M . Δg – m . g = 0

-  Or P_A = P_B car il y a équilibre dans le cas (1).

-   or P_A = P_B car il y a équilibre dans le cas (1).

-  On peut déduire la relation :

- 

3)- application numérique :

-  .

4)- Comparaison :

-  Valeur théorique

-  .

-  Précision :  4 %

5)- La poussée d'ARCHIMède ne change pas car les boules sont identiques.

Mesure de la constante de gravitation par Cavendish (1798).

Pour mesurer la constante G, Cavendish utilise, en 1798, une balance de torsion, (cf. schéma suivant).

Un fil de torsion (constante C) vertical supporte par son centre un fléau horizontal de longueur ℓ, aux extrémités

B et B’ duquel sont fixées deux petites sphères de même masse m.

Celles-ci peuvent être soumises à l’attraction de deux grosses boules de même masse M dont mes centres E et

E’ sont situés dans le plan horizontal du fléau BB’.

En l’absence des boules, le fléau occupe la position d’équilibre telle que la torsion du fil soit nulle.

Les boules sont amenées dans deux positions symétriques par rapport au milieu O du fléau telles

que les directions (EB) et E’B’) soient perpendiculaires à la direction du fléau au repos et que EB = E’B’ = d.

En raison des interactions gravitationnelles entre boules et petites sphères, l’équilibre initial est rompu :

le fléau tourne d’un angle α, tordant l’extrémité O du fil du même angle.

1)- Exprimer littéralement la valeur de chaque force d’interaction gravitationnelle entre une petite sphère

et une boule en fonction de m, M, d et G.

Indication : Négliger l’interaction entre les sphères et les boules les plus éloignées.

2)- Écrire le moment du couple dû aux forces gravitationnelles agissant sur le fléau en fonction de m, M, d et ℓ.

3)- Exprimer la condition d’équilibre du fléau et en déduire une relation entre m, M, d, ℓ, C, α et G.

4)- Une expérience ayant été réalisée avec m = 50 g,

M = 30 kg, C = 5,0 x 10 ^{– 7} N.m.rad ^{– 1}, ℓ = 10 cm et d = 15 cm

On demande de déterminer la valeur de l’angle α en radian.

5)- Pour mesurer la valeur de l’angle α, il est judicieux de mettre en œuvre une technique due au physicien Poggendorf (1796 – 1877) ;

un petit miroir est collé en O sur le fil.

Éclairé par le faisceau d’une lanterne, il donne un spot lumineux sur une règle graduée. En l’absence de torsion du fil, le spot coïncide avec le zéro de la règle.

Lorsque le fil est tordu d’un angle α, le faisceau ayant tourné d’un angle 2 α, le spot s’est déplacé d’une longueur δ sur la règle.

La règle est située à la distance D = 5,0 m du fil.

a)- Déterminer la longueur δ du déplacement.

b)- Conclure quant à la faisabilité de l’expérience.

1)- Expression littérale de chaque force :

-  Schéma :

Cliquer sur l'image pour l'agrandir

2)- Moment du couple :

3)- Condition d'équilibre :

-   : Représente le couple de torsion du fil, il est proportionnel à la constante de torsion C

et à l’angle de torsion α en radian :

-  

-  Le signe (–) provient de l’orientation choisie et du fait que le fil s’oppose à la déformation.

4)- Valeur de l'angle en radian.

5)- Technique de POGGENDORF (1796-1877).

a)-  Longueur du déplacement :

b)-  L'expérience est possible avec un fil de torsion en quartz.