|
Phys
N° 09 :
|
|
|
|
|
1)- Étude de la trajectoire d'une particule
chargée
dans un champ magnétique uniforme. |
-
Le produit vectoriel de
deux vecteurs
et
faisant entre eux un angle
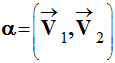, est un vecteur:
-
Dont la direction est
perpendiculaire au plan défini par
et
,
-
Le sens est tel que le
trièdre
,
et
est
direct,
-
La norme
.
-
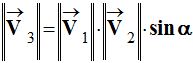Le produit vectoriel
est noté :
.
-
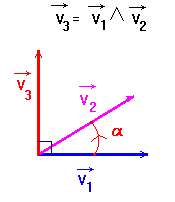
Règle : Tire-bouchon,
main gauche, main droite. Représentation conventionnelle
-
Main gauche :
3)- Propriétés du produit
vectoriel.
-
Le produit vectoriel
n'est pas commutatif et
.
|
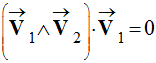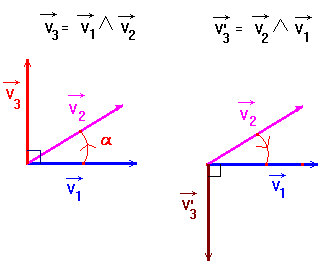
- Il comprend :
- Une ampoule sphérique
contenant un gaz raréfié (H2) qui permet de
visualiser la
trajectoire des électrons (luminescence).
- Un canon à électrons
qui donne un faisceau d'électrons monocinétique. - Cette ampoule est située entre deux bobines de Helmholtz. - Ces bobines sont parcourues par un courant d'intensité I.
- Le champ magnétique
- La valeur du champ magnétique est proportionnelle à l'intensité du courant qui circule dans les bobines.
- L'ampoule peut tourner autour d'un axe vertical.
- On peut ainsi changer
la direction de la vitesse initiale
|
|
- Le champ magnétique est
uniforme,
- Orientation : règle de
la main droite : doigt dans le sens du courant et
le pouce écarté donne la
direction et le sens de
- Direction : axe commun
des deux bobines.
- Indiquer
sur les figures 1 et 2 le sens du courant dans les bobines, les faces des
bobines et représenter le vecteur champ magnétique
|
Figure
1 :
Vue de face Vue
de profil
Cliquer sur l'image pour
l'agrandir
b)-
Expérience 1.
|
- Que peut-on dire des
vecteurs
-
- Premier cas, on fixe
l'intensité du courant
I
= 0 :
- Quelle est dans ce cas
la valeur de champ magnétique B ?
- Quelle est la
trajectoire décrite par le faisceau d'électrons ?
- Conclusion. - 1ier cas : I = 0 => B = 0, - La trajectoire des électrons est rectiligne,
-
les électrons ne subissent aucune
action.
- Deuxième cas, on augmente la valeur de l'intensité du courant I > 0
:
- Comment varie
B
quand I augmente ?
- Quelle est la
trajectoire décrite par le faisceau d'électrons ?
- Conclusion.
-
- La
trajectoire s'incurve puis devient circulaire.
- L'électron
subit une action mécanique. |
c)-
Expérience 2.
|
-
Que peut-on dire des
vecteurs
-
- Premier cas, on fixe
l'intensité du courant
I
= 0 :
- Quelle est dans ce cas
la valeur de champ magnétique B ?
- Quelle est la
trajectoire décrite par le faisceau d'électrons ?
- 1ier
cas :
I = 0 =>
B =
0,
trajectoire rectiligne, aucune action
- Deuxième cas, on augmente la valeur de l'intensité du courant
I
> 0 :
- Comment varie
B
quand I augmente ?
- Quelle est la
trajectoire décrite par le faisceau d'électrons ?
-
Conclusion.
- 2ième
cas
:
-
Si
qui a pour effet de dévier le faisceau d'électrons.
- Si
|
III- La force magnétique : force de Lorentz
.
-
La force
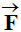exercée
par un champ magnétique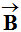
sur une charge
q
animée d'une vitesse
a
pour expression :
|
Caractéristiques de
|
- Direction
|
|
- sens,
|
|
|
- valeur : F = |q| . v . B . sin α
- (Au niveau de la
terminale,
|
-
remarque :
-
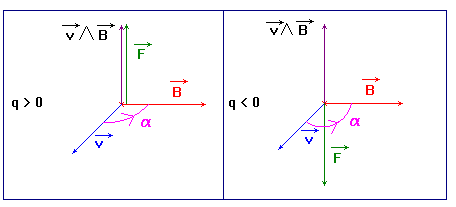
Que peut-on dire du
travail reçu par un électron se déplaçant dans un champ magnétique uniforme ?
-
Le travail
de la force de Lorentz est nul car la direction de la force est perpendiculaire
au déplacement.
-
L'énergie cinétique
d'un électron varie-t-elle ?
-
L'énergie
cinétique ne varie pas puisque la force ne travaille pas.
-
Quels sont les effets
de la force de Lorentz sur le vecteur vitesse d'un électron ?
-
Les
électrons se déplacent à la même vitesse, mais la direction change à chaque
instant.
1)- Étude de la trajectoire
d'une particule chargée dans un champ magnétique uniforme.
|
- Dans une ampoule sphérique en verre contenant un gaz sous faible pression, on étudie la trajectoire suivie par un pinceau d'électrons homocinétiques soumis à
l'action
d'un champ magnétique uniforme, de vecteur champ
- L'ampoule est placée entre deux bobines d'Helmholtz (bobines coaxiales) où
règne le champ magnétique
(c'est-à-dire perpendiculairement au plan de la
figure 1). - Le pinceau d'électrons est créé par un canon C dans lequel les électrons, émis à
une vitesse
négligeable sont accélérés par une tension U.
- Les électrons sortent
du canon avec une vitesse représentée par le vecteur
vertical,
orienté de gauche à droite (voir figure 1 : vue de face).
- on observe une trajectoire circulaire de rayon R.
- On néglige le poids des électrons
devant la valeur de la force de Lorentz.
- Dans le cas présent,
a)- Donner l'expression de
la force électromagnétique
électron à l'instant t. En déduire les caractéristiques du vecteur force.
Faire un schéma.
- Force de Lorentz :
|
|
Caractéristiques de : |
- Direction
|
|
- sens,
|
|
|
- valeur : F =
e .
v .
B car |
|
|
|
|
|
b)- Après avoir précisé le
référentiel d'étude et choisi le repère d'Espace, appliquer le théorème du
centre d'inertie.
- Dans l'exercice, on
néglige l'effet du poids devant la force magnétique.
- Le théorème du centre
d'inertie dans le référentiel galiléen permet d'écrire que :
-
c)-
Donner l'expression du
vecteur accélération
- De (1) et (2), on tire
que :
- On peut remarquer que
puisque le mouvement est circulaire. a)- Montrer alors
que le mouvement des électrons se fait dans un plan.
- Conditions initiales :
-
- De l'expression (3), on déduit qu'à chaque instant, le vecteur accélération est
perpendiculaire au
vecteur champ magnétique (propriété du produit vectoriel).
- En conséquence, le
vecteur accélération est contenu dans le plan xOy.
- On en déduit les
coordonnées du vecteur accélération dans le repère choisi.
- Du fait des conditions
initiales, le mouvement s'effectue dans le plan xOy.
- Il n'y a pas de
composante suivant l'axe z'z.
b)-
Monter que le mouvement
des électrons est circulaire uniforme.
Il faut utiliser le repère de Frenet et donner l'expression
du vecteur
- Comme il faut montrer que le mouvement est circulaire, on utilise le repère de Frenet.
- On donne l'expression de
-
- On peut en déduire
l'expression du vecteur accélération dans
le repère de
Frenet :
-
-
- On en déduit les
coordonnées du vecteur accélération dans le repère de Frenet : |
|
|
La composante
tangentielle de l'accélération est nulle |
|
En
conséquence : v = cte = v0
le mouvement de la particule est
uniforme |
|
|
D'autre part
:
|
|
c)- Établir l'expression de R (rayon du cercle) en fonction de m, v0, B et e (e représente la charge élémentaire et
m la masse de
l'électron).
-
-
A.N :
-
d)-
Indiquer sur la figure
1, la direction et le sens de la force
Indiquer le sens du courant dans les bobines.
-
Voir figure 1 : |
Cliquer sur l'image pour
l'agrandir
|
-
On utilise ce
dispositif pour déterminer expérimentalement le rapport
e)-
Comment peut-on mesurer
pratiquement la valeur de B ?
On trouve
B = 1,25
× 10 –3 T.
-
Mesure à l'aide d'un
Teslamètre. f)- Comment peut-on mesurer pratiquement le diamètre D de la trajectoire circulaire suivie par les électrons ?
On trouve D =
6,0 cm.
-
Mesure à l'aide d'une
règle graduée. g)- Montrer que v0, vitesse initiale des électrons à la sortie du canon, s'exprime en fonction de la charge massique de l'électron et de la tension accélératrice U.
En
déduire que la charge massique
-
Calculer numériquement
- Données : m = 9,10 × 10–31 kg ; B = 1,25 × 10 –3 T ;
-
e = 1,60
× 10 –19 C
; v0 = 6,59
× 10 6 m
/ s
-
En utilisant le
théorème de l'énergie cinétique :
-
Attention :
l’électron porte une charge négative
-
Schéma :
-
-
-
En utilisant (4) et
(5), on trouve :
-
-
A.N :
-
-
Vérification :
-
|
a)-
Énoncé :|
- Un électron arrive dans le vide avec une vitesse initiale v0, de direction (OA) et orienté de O vers A ( v0 = 6,00 x 106 m / s),
au point d'origine
O
d'un référentiel Galiléen.
-
Il est alors soumis à
l'action d'un champ magnétique uniforme créé dans une
région de l'espace
délimitée par le rectangle.
-
On suppose que la
distance d est très petite devant la distance
L. b)- Quelle est la nature du mouvement d'un électron entre O et M ? Justifier la réponse.
Calculer la valeur du rayon de l'arc de cercle décrit
par l'électron. |
-
Solution :
|
Système : |
On choisit un
électron e– |
|
Référentiel et repère : |
On choisit
comme référentiel : le dispositif. Le référentiel est un référentiel Terrestre, il est considéré comme
Galiléen. Le repère
d’étude est lié au référentiel.
|
|
Bilan des forces : |
L’électron est soumis à la force magnétique
Remarque : on
peut négliger l’effet du poids devant celui de la force magnétique.
|
|
Étude
dynamique : |
Dans le
référentiel galiléen, on applique le théorème du centre d’inertie :
En conséquence, le vecteur accélération est perpendiculaire au vecteur vitesse ceci à chaque instant (propriété du produit vectoriel). |
|
Coordonnées du vecteur
accélération : |
On travaille
dans le repère de Frenet :
Comme
|
|
Conclusion : |
Le mouvement
de l’électron est circulaire uniforme.
|
|
-
Ils décrivent un arc de cercle de rayon
:
-
Application numérique :
-
c)- Quelle est la nature du mouvement d'un électron entre M et B ?
(On néglige l'effet du
poids sur ce parcours) - Comme on néglige l'effet du poids sur le trajet MB,
on peut considérer que
le mouvement des électrons sur ce trajet très court est
rectiligne uniforme.
-
MB
a pour direction la tangente à l'arc de cercle au point
M
: CM
-
On utilise
l'approximation suivante :
-
On considère que
l'angle
a
est petit en radian, en conséquence :
-
sin
α ≈ tan
α
≈ α et
-
Exprimer
AB =Dm
(déflexion magnétique en fonction de
R,
d et
L.
-
Vérifier que Dm
est fonction linéaire du champ magnétique appliqué.
-
Calculer
Dm.
-
Données : (d
=
1,00 cm ; L = 40,0 cm
; B = 1,25 × 10 –3 T)
-
Solution :
-
Dm
= AK +
KB (1)
-
D'autre part :
-
On en déduit :
KB
≈ α .
L (2)
-
Part construction, on
remarque que :
-
AK
= OJ =
OC –
CJ =
R –
R . cos
α
(3)
-
En utilisant
l'approximation,
-
-
Mais
-
-
-
Application numérique :
-
|
- Dans la région de l'espace où règne le champ magnétique, les électrons sont déviés.
5)- Le spectrographe de
masse.
|
On ne tiendra pas compte
de la pesanteur.
a)- On considère deux plaques P et N, conductrices, parallèles, verticales et distantes de d = 10,0 cm. La tension entre les plaques est U = VP – VN = 6,00 × 104 V. Une source émet des ions argent
Ag+,
avec une vitesse nulle, au travers d’une fente S placée dans la plaque P.
-
Quelle est la nature du
mouvement des ions
Ag+
entre les
deux plaques ?
-
nature
du mouvement des ions argent entre les plaques
P
et
N. |
|
Système : |
On choisit un
électron e- |
|
Référentiel
et repère : |
On choisit comme
référentiel : le dispositif. Le référentiel est un référentiel Terrestre, il est considéré comme Galiléen. Le repère d’étude
est lié au référentiel.
|
|
Bilan des
forces : |
L’électron est
soumis à la force électrique
On
néglige l’effet du poids devant celui de la force magnétique. |
|
Étude
dynamique : |
Dans le
référentiel galiléen, on applique le théorème du centre d’inertie :
En conséquence :
|
|
Coordonnées des différents
vecteurs : |
Le mouvement d'un ion argent est rectiligne uniformément accéléré, entre les plaques P et N, car le vecteur position, le vecteur vitesse et le vecteur accélération ont même direction et même sens et le vecteur accélération est constant. |
|
-
Quelle est l’expression
littérale de la vitesse des ions à leur arrivée en
O, sur la
plaque
N
?
-
Expression
littérale de la vitesse.
-
Il faut
utiliser le théorème de l'énergie cinétique.
- Dans le référentiel d'étude supposé Galiléen, la variation d'énergie cinétique est égale
à la somme des travaux des forces.
-
-
expression
de la vitesse :
-
-
L’argent est un mélange
de 2 isotopes 107Ag
et 109 Ag.
- Calculer numériquement la valeur de la vitesse de chacun des isotopes à son arrivée en O.
(mp ≈ mn
≈ 1,66
×
10
–
27 kg).
-
Valeur
numérique de la valeur de la vitesse pour chaque isotope.
-
b)- Les ions Ag+ traversent en O la plaque N par une fente et sont alors soumis à
un champ magnétique uniforme, de vecteur
-
Montrer qu’ils sont
animés d’un mouvement circulaire uniforme. |
Solution :
|
Système : |
On
choisit l’ion
Ag+ |
|
Référentiel
et repère : |
On choisit comme
référentiel : ledispositif. Le référentiel est un référentiel Terrestre,
il est considéré comme
Galiléen. Le repère d’étude
est lié au référentiel. |
|
Bilan des
forces : |
L’électron est soumis à la force magnétique
et
à son poids
Remarque : on peut négliger l’effet du poids devant celui de la force magnétique. |
|
Étude
dynamique : |
Dans le référentiel galiléen, on applique le théorème du centre d’inertie :
En conséquence, le vecteur accélération est perpendiculaire au vecteur vitesse ceci à chaque instant (propriété du produit vectoriel). |
|
Coordonnées du vecteur accélération : |
On travaille dans
le repère de Frenet :
Comme et comme :
|
|
Conclusion : |
Le mouvement de
l’électron est circulaire uniforme.
|
|
-
Établir
l’expression du rayon de courbure
R
en fonction de
e,
U,
B
et de la
masse
m
d’un ion.
-
À
l’aide
des relations
-
On tire :
-
Calculer numériquement
R
pour chaque isotope si
B
= 1,0 T.
-
c)- À leur sortie du champ magnétique, les ions passent au travers d’une large fente
et sont captés par un
fil métallique
f
relié à la terre à travers un galvanomètre
sensible
G.
-
À
quelles distances
x
de O
faut-il placer le fil f pour recevoir respectivement
les ions 107Ag+ et
109 Ag+
?
-
Position
du fil F pour chaque isotope :
-
x107
= 2 R107 => x107
≈ 0,730 m
-
x109
= 2 R109 => x107
≈ 0,737 m
- Pour les distances x précédentes, le galvanomètre indique les courants respectifs de 61,61 mA et 58,38 mA.
Quelle est la composition isotopique de l’argent ?
-
(Charge élémentaire :
e
= 1,60
× 10 –19 C)
|
|
|
|
|
à 
, 
le mouvement
est circulaire.
(4) 
. 
et comme : 
