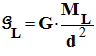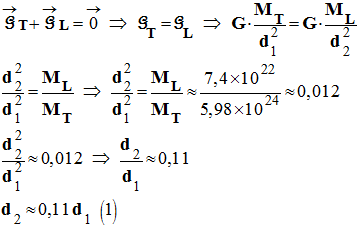|
Champs et forces. Exercices. |
|
|
|
I- Exercice 7 page 213. Cartographier un champ scalaire.
|
Que faut-il mesurer pour cartographier un champ de température ? |
|
De façon générale, pour cartographier un champ, on détermine les caractéristiques de ce champ en certains points de l’espace et on en donne une représentation : Dans le cas présent, on est en présence d’un champ scalaire, il suffit de donner la température de certains points de l’espace étudié. Exemple :
|
II- Exercice 9 page 213. Exploiter des lignes de champ vectoriel.
|
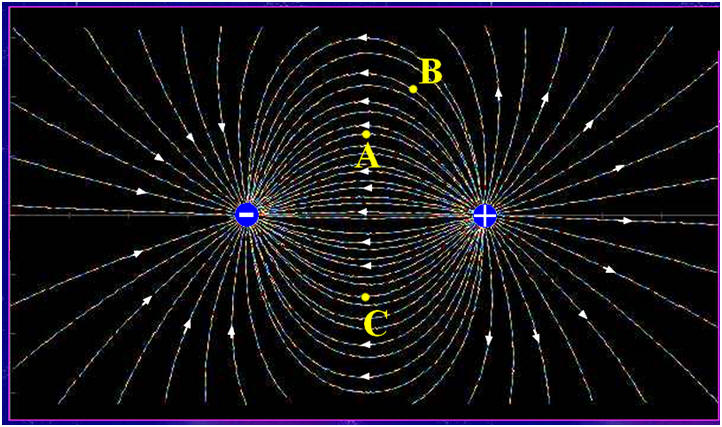
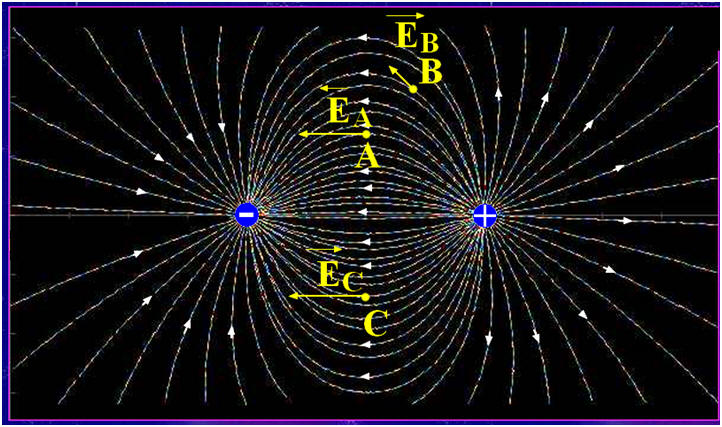
1)- Qu’appelle-t-on ligne de champ vectoriel ? 2)- Reproduire en partie la carte de champ électrostatique créé par deux champs électriques et dessiner sans souci d’échelle, le vecteur champ électrostatique en A, B et C. |
|
1)- Ligne de champ vectoriel : -
Une ligne de champ
vectoriel est une ligne tangente en chacun de ses
points au vecteur champ.
- Elle est orientée par une
flèche dans le même sens que celui du champ. 2)-
Champ électrostatique créé par deux champs
électriques :
Animation CabriJava |
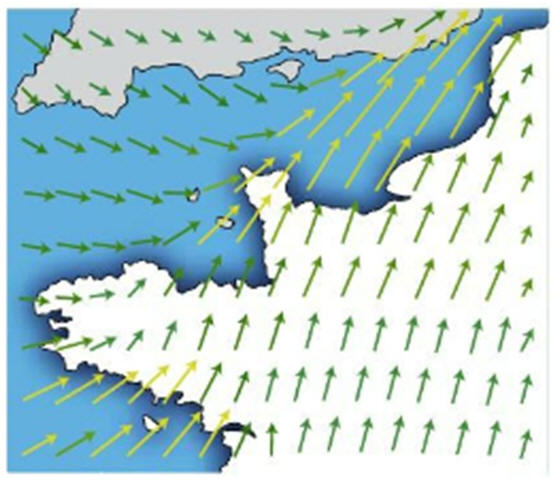
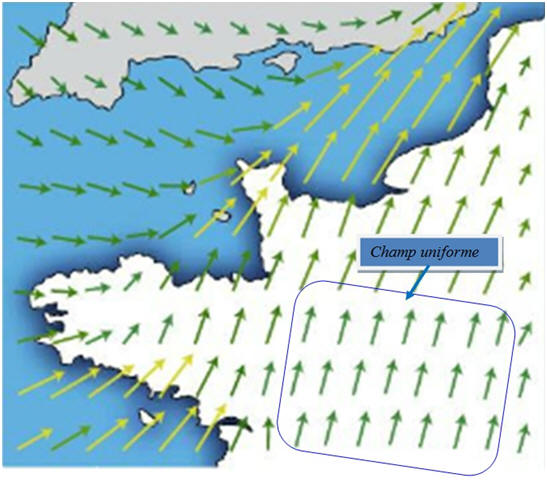
III- Exercice 11 page 213. Lire une carte de vitesse des vents.
|
1)- Champ vectoriel ou champ scalaire : ► Grandeur vectorielle : - Une grandeur vectorielle (en physique) est caractérisée par : - Son origine - Sa direction et son sens, - Sa valeur associée à une unité - Un champ vectoriel est défini par un vecteur (direction, sens, valeur et unité) en chaque point. -
Pour connaître le
vent en un point de l’espace, il faut connaître :
- la
direction, le sens et la valeur du vent. -
On est bien en
présence d’un champ vectoriel.
2)-
Champ vectoriel uniforme : ► Un champ uniforme est un champ dont les caractéristiques ne dépendent pas du point de l’espace considéré. - Le vecteur qui représente le champ a : - La même direction, le même sens et la même valeur dans l’espace considéré. -
On peut représenter
ce champ par un vecteur qui indique, la direction,
le sens et la valeur du champ dans tout l’espace
considéré.
3)-
Zone géographique où le champ est uniforme : -
Dans cette zone, les
flèches ont toutes la même longueur.
- Elles indiquent
la même direction et ont le même sens. |
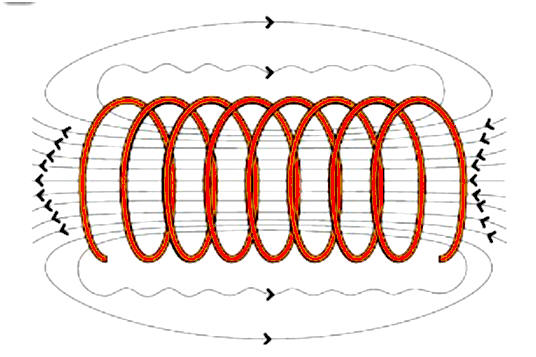
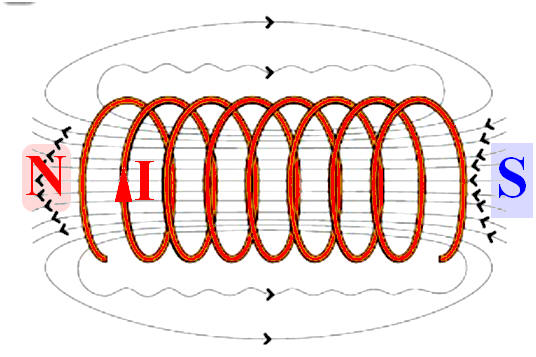
IV- Exercice 12 page 213. Identifier les pôles magnétiques.
|
1)- Orientation des lignes de champ à l’extérieur de l’aimant ou de la bobine : -
Les lignes de champ
sont orientées dans le sens du champ magnétique du
pôle Nord vers le pôle Sud N → S de la source
de champ.
2)-
Les pôles de la bobine : |
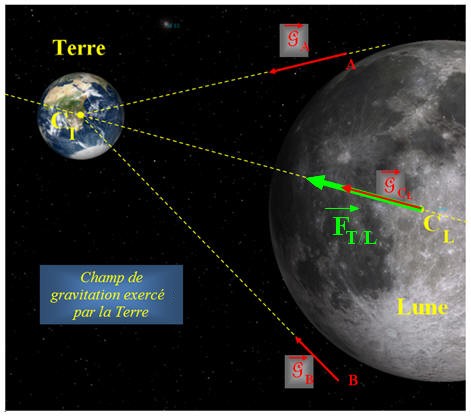
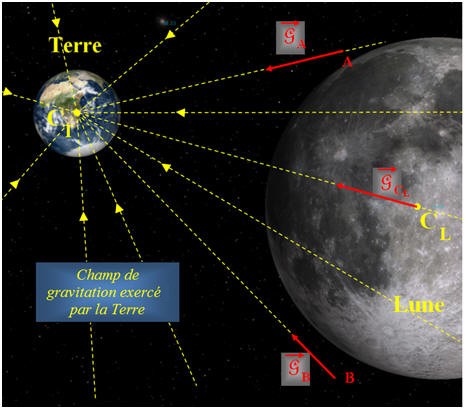
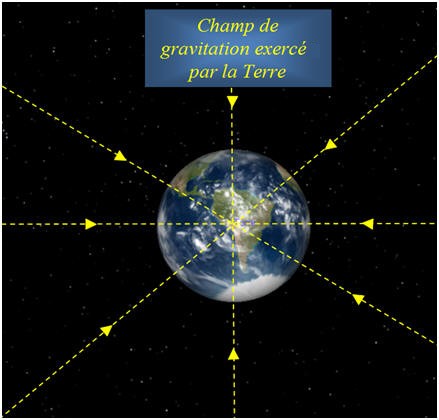
V- Exercice 18 page 215. La Terre a rendez-vous avec la Lune.
|
Le centre de la Lune se situe
en moyenne à une distance
d = 3,84
Située dans le
champ de gravitation de la Terre, la Lune subit son
attraction.
1)-
Schématiser la situation sans souci d’échelle. 2)-
Représenter des lignes de champ gravitationnel
terrestre. 3)-
Exprimer puis calculer la valeur de la force
d’attraction gravitationnelle exercée par la Terre
sur la Lune. - Données : - Masse de la Terre : MT = 5,98 x 1024 kg ; - Masse de la Lune ML = 7,4 x 1022 kg ; - G = 6,67 x 10– 11 N.m2 . kg–2 |
|
1)-
Schéma de la situation :
2)-
Lignes de champ : 3)-
Force d’attraction gravitationnelle exercée par la
Terre sur la Lune : -
Expression de la
force -
- Valeur de la force : -
|
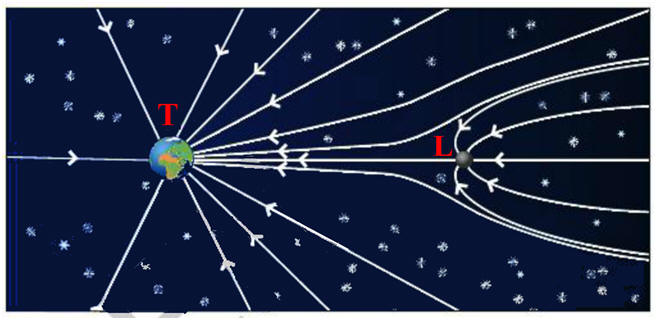
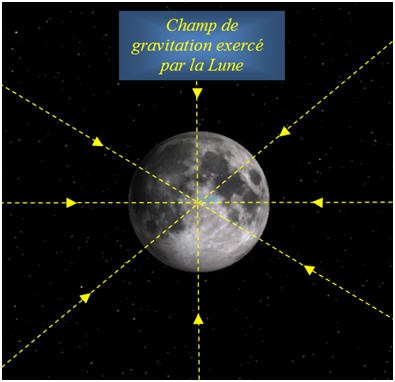
VI- Exercice 20 page 215. Point d’équigravité.
|
1)-
Schématiser la Terre et représenter des lignes de
champ gravitationnel de la terrestre.
2)-
Faire de même pour la Lune, sur un autre schéma. 3)-
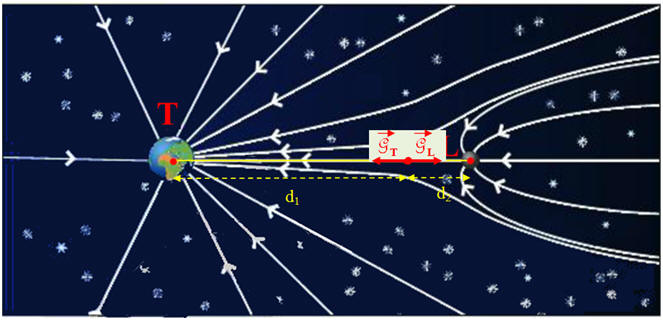
La carte de champ gravitationnel ci-dessous
représente quelqueslignes de champ créées par la
Terre et la Lune. Quel astre déforme le plus les
lignes de champ gravitationnel de l’autre astre ?
Justifier en comparant les valeurs des masses. 4)-
Champ de gravitation : a)- b)- - Données : - Masse de la Terre : MT = 5,98 × 1024 kg ; - Masse de la Lune ML = 7,4 × 1022 kg ; - Distance moyenne Terre – Lune : d = 3,84 × 108 m -
G = 6,67
× 10–
11 N.m2 . kg–2
|
|
1)- Schématisation des lignes de champ : -
Cas de la Terre :
2)-
Schéma des lignes de champ : -
Cas de la Lune :
3)-
L’astre qui déforme le plus les lignes de champ
gravitationnel de l’autre astre est la Terre : -
En un point de
l’espace :
-
Pour des distances
identiques, le champ de gravitation de la Terre a
une influence plus importante
que celui de la Lune
car la Terre est environ 80 fois plus lourde que la
Lune. - Les lignes de champ gravitationnel de la Terre sont très peu déformées par la présence de la Lune. -
Les lignes de champ
gravitationnel de la Lune sont déformées par la
présence de la Terre.
4)-
Champ de gravitation : a)- - Pour que la somme des deux vecteurs soit nulle, il faut que : -
Les deux vecteurs
aient la même direction, des sens opposés et la même
valeur.
b)- point ou les vecteurs
champs gravitationnels lunaire et terrestre se
compensent, est la ligne de champ qui relie les
centres de la Terre et de la Lune : - Pour aller plus loin : On peut déterminer, la valeur de d1 : - Au point d’équigravité : -
- D’autre part : d1 + d2 = d = 3,84 x 108 m (2) - En combinant (1) et (2), on tire : - d1 ≈ 3,5 x 108 m et d2 ≈ 3,8 x 107 m |
VII- Exercice 24 page 217. Le temps est à l’orage.
|
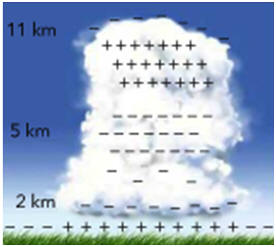
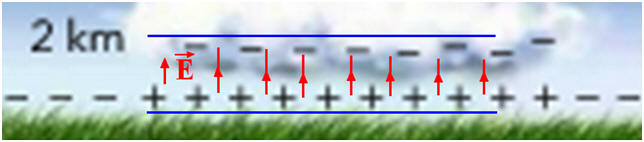
Par beau temps, le champ électrostatique au voisinage de la surface de la Terre est quasiment uniforme. Sa valeur est de l’ordre de 150 V / m et est dirigé vers le sol. Par temps d’orage, on observe la formation de cumulo-nimbus. Ces nuages ont une base quasiment horizontale, chargée négativement. Au voisinage de cette base, le sol se charge positivement. L’accumulation de charges électriques est telle que la valeur du champ électrostatique peut dépasser 20 kV / m. Le champ est si intense que l’air est ionisé, ce qui le rend beaucoup plus conducteur qu’habituellement. Une décharge électrique est donc possible, c’est l’éclair.
1)- Par beau temps, quel est le signe de la charge électrique de la surface du sol ? 2)- Expliquer pourquoi la surface du sol se charge positivement sous un cumulo-nimbus. 3)- En considérant un sol horizontal et plan, par quoi peut-on modéliser le système formé par le sol et la partie inférieure du cumulo-nimbus ? 4)- Champ électrostatique : a)-
Que peut-on dire du champ
électrostatique entre le sol et la base du nuage ?
b)-
Reproduire le schéma
ci-dessus et représenter quelques lignes de champ
électrostatique.
|
|
1)- Signe de la charge électrique de la surface du sol : - Par beau temps, le champ électrostatique au voisinage de la surface de la Terre est quasiment uniforme. - Sa valeur est de l’ordre de 150 V / m et est dirigé vers le sol. - Le champ est dirigé dans le sens des potentiels décroissants : la surface du sol est chargée négativement. 2)- La surface du sol se charge positivement sous un cumulo-nimbus : - La base du nuage est chargée négativement. - En conséquence, il repousse les charges négatives situées au niveau du sol et attire les charges positives qui viennent se mettre en regard du nuage. - Le nuage change la répartition des charges au niveau du sol et le sol en regard du nuage se charge positivement. 3)- Modélisation : - On peut modéliser l’ensemble : - Le sol horizontal est plan chargé positivement - Et la base quasiment horizontale, chargée négativement du cumulo-nimbus - Par un condensateur plan chargé. (voir le schéma au-dessous) 4)- Champ électrostatique : a)- Champ électrostatique entre le sol et la base du nuage : - Tout se passe comme si on était en présence d’un condensateur chargé. - Le champ entre le sol et la base du nuage est pratiquement uniforme et il est orienté du sol vers la base du nuage. b)- Schéma de la situation : ligne de champ électrostatique. |
VIII- Exercice 25 page 217. Champ géomagnétique.
|
À en perdre le nord !
Les physiciens
et les navigateurs savent depuis longtemps que la
Terre possède deux pôles Nord distincts ! Le pôle Nord géographique, situé au milieu de l’océan Arctique, est le lieu où passe l’axe de rotation de la Terre,
c’est le Nord des cartes géographiques. Le pôle magnétique qui attire l’aiguille de la boussole, est le point de
l’hémisphère géographique pour lequel la
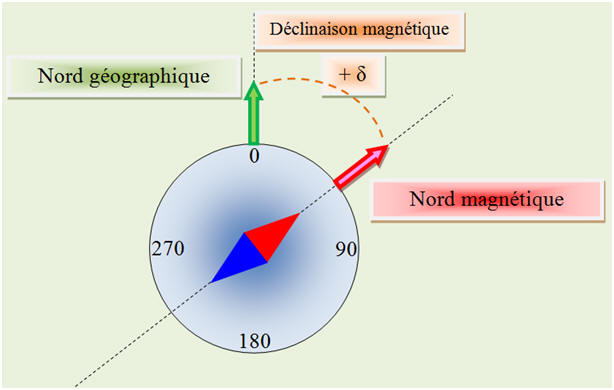
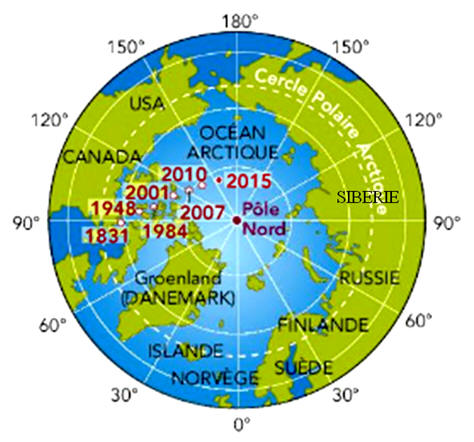
ligne de champ magnétique est verticale. Il n’est pas confondu avec le pôle géographique. Le pôle magnétique de l’hémisphère Nord au sens géographique, est appelé par abus de langage pôle Nord magnétique par les géographes. Les pôles géographiques sont fixes, alors que les pôles magnétiques se déplacent en permanence. L’origine de ces déplacements se trouve au cœur de notre planète où des mouvements de matière modifient le champ magnétique terrestre. En 1831, quand le navigateur anglais J.C Ross l’a localisé pour la première fois, le pôle Nord magnétique se trouvait au Cap Adélaïde, dans le nord du Canada. Jusqu’en 1980, il s’est déplacé de 10 km par an environ. Le mouvement s’est ensuite accéléré, pour se stabiliser à une vitesse d’environ 55 km par an. À ce rythme, il pourrait atteindre les côtes sibériennes en 2040. Pendant longtemps, l’écart entre les directions du Nord magnétique et du Nord géographique, appelé « déclinaison magnétique» et noté δ, a joué un rôle essentiel dans le transport maritime. La déclinaison, qui se mesure localement, devrait être régulièrement mise à jour sur les cartes, pour permettre de corriger les relevés magnétiques et positionner les navires sur les cartes. De nos jours, les systèmes de positionnement par satellite (GPS) fournissent une localisation indépendante du champ magnétique terrestre.
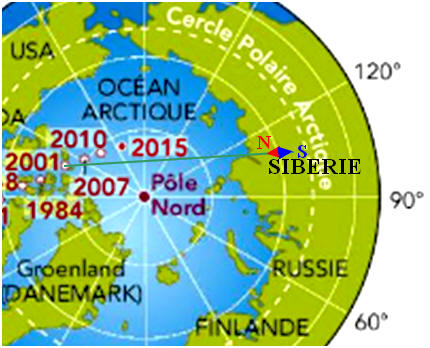
Déplacement du pôle magnétique de l’hémisphère Nord au cours du temps. La position 2015 est une prévision issue d’un modèle construit à partir de l’étude des déplacements précédents. 1)- Expliquer pourquoi une boussole n’indique pas toujours le Nord géographique. 2)- Place du Nord géographique : a)- En 2001, pour un explorateur au Groenland, le Nord géographique se trouve-t-il à l’Est ou à l’Ouest de la direction indiquée par la boussole ? b)- Même question pour un explorateur en Sibérie. 3)- Le champ magnétique terrestre s’est déjà inversé plusieurs fois. Ce phénomène a été découvert en France au début du XXe siècle par le géophysicien français Bernard BRUNHES. Qu’a-t-il étudié pour montrer cette inversion ? |
|
1)- Indication donnée par la boussole : - Une boussole indique le pôle Nord magnétique. - Comme le pôle Nord géographique et le pôle Nord magnétique ne sont pas confondus, la boussole ne donne pas toujours le pôle Nord géographique. 2)- Place du Nord géographique : a)- Explorateur au Groenland en 2001 : - Le pôle Nord géographique se trouvait à l’Est de la direction indiquée par la boussole.
b)- Explorateur en Sibérie : - Le pôle Nord géographique se trouvait à l’Ouest de la direction indiquée par la boussole.
3)- Inversion du champ magnétique terrestre : - Le champ magnétique terrestre s'inverse selon un rythme irrégulier. - La dernière modification est survenue il y a 790 000 ans. - Ce dernier changement a été nommé l'inversion BRUNHES-MATUYAMA. - Vers 1906, le physicien français Bernard Brunhes note que dans certaines coulées delave du Massif central, qui conservent la mémoire de la direction du champ magnétique terrestre, le champ magnétique était inversé. - Ce phénomène a été confirmé par le Japonais MATUYAMA qui suggéra l'existence d'inversions répétées du champ géomagnétique au cours des temps géologiques. |
|
|



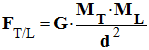
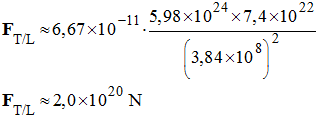
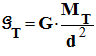 et
et