|
|
La lumière : un flux de photons |
|
|
|
|
|
1)- Modèle ondulatoire : Rappels
et compléments. |
|
1)- Description de l’effet
photoélectrique : 3)- Bilan énergétique et
interprétation à l’aide du modèle particulaire. |
|
III- L’absorption ou
l’émission de photons. 1)- Émission et absorption de
photons. 2)- Absorption de photons et
cellule photoélectrique. 3)- Émission de photons et diodes
électroluminescentes (DEL). |
|
1)- Rendement d’une cellule
photovoltaïque.
QCM r
La lumière : un flux de
photons Effet photoélectrique L’absorption ou
l’émission de photons |
|
Exercices : énoncé avec correction.
1)- Exercice 03 page 416 : Connaître l’effet
photoélectrique. 2)- Exercice 05 Page 416 : Interpréter l’effet
photoélectrique. 3)- Exercice 07 page 416 : Réaliser un bilan
d’énergie. 4)- Exercice 09 page 417 : Calculer des rendements. 5)- Exercice 13 page 417 : Conservation de
l’énergie. 6)- Exercice 15 page 418 : Énergie cinétique des
électrons. 7)- Exercice 17 page 419 : Comparaison de
l’effet photovolaïque. 8)- DS 01 : Effet photovoltaïque et panneaux
photovoltaïques (60 min) 9)- Préparation à l’ECE : Rendement d’une
cellule photovoltaïque. |
|
QCM r
La lumière : un flux
de photons Effet photoélectrique L’absorption ou
l’émission de photons |
I-
La lumière.
1)- Modèle ondulatoire :
Rappels et compléments.
-
La lumière a une
nature ondulatoire.
-
On parle de l’onde
lumineuse.
-
L’onde lumineuse
résulte de la propagation d’une perturbation électromagnétique dans les milieux
transparents.
-
Les ondes
lumineuses périodiques sont appelées des radiations.
-
Contrairement aux
ondes mécaniques, la propagation des ondes lumineuses ne nécessite pas de
support matériel.
-
La lumière peut se
propager dans le vide.
-
La lumière est une
onde transversale : la direction de propagation est perpendiculaire à la
direction de la perturbation.
-
L’onde lumineuse
résulte de la propagation simultanée d’une perturbation électrique et d’une
perturbation magnétique.
-
Dans le vide ou
dans les milieux transparents homogènes, la lumière se propage en ligne droite.
-
Une radiation
lumineuse est caractérisée par :
-
Sa fréquence ν
(en Hz) ou sa période T
(en s).
-
Sa longueur d’onde dans le vide
λ0.
-
Remarque :
-
La fréquence d’une
radiation lumineuse ne dépend pas du milieu de propagation alors que la longueur
d’onde dépend du milieu de propagation.
►
Relation
fondamentale :
|
|
λ0 :
longueur d’onde dans le vide (m) |
|
c :
vitesse de la lumière dans le vide (m . s–1) |
|
|
T :
période (s) |
|
|
ν :
fréquence (Hertz) |
-
Remarque : pour les
radiations lumineuses, on préfère utiliser la lettre grecque ‘’nu’’.
-
De manière
générale, on caractérise une radiation lumineuse par sa longueur d’onde dans le
vide.
-
Complément : l’œil
humain n’est sensible qu’à certaines radiations lumineuses.
-
La
vitesse d’une onde lumineuse dépend du milieu de propagation comme la longueur
d’onde λ.
-
La fréquence
ν et
ainsi la période T
ne dépendent pas du milieu de propagation.
- Dans le milieu d’indice n :
- ![]()
-
λ
= v
. T
-
Dans le vide :
-
λ0
= c .
T
-
On en déduit :
-
λ0
= n .
λ
-
Dans les milieux transparents, la
lumière se déplace moins vite que dans le vide.
-
La vitesse de la lumière dans l’air est
peu différente de celle dans le vide.
-
Comme valeur
approchée dans l’air et le vide, on choisit la valeur suivante :
|
cair
≈
c
≈
3,00 × 108
m / s |
b)-
Les domaines d’application.
-
Le domaine de
radiations lumineuses visibles s’étend de 400 nm (violet) à 780 nm (rouge).
-
Domaine de
longueurs d’onde correspondant :
400 nm ≤ λ
≤ 780 nm
-
Spectre des ondes
électromagnétiques :
-
Le spectre des
ondes électromagnétiques est découpé, de façon arbitraire, en divers domaines.
-
Le document
suivant, donne des exemples de rayonnements dans divers domaines du spectre
électromagnétique.
-
On remarque que la
lumière visible ne représente qu’une infime partie du spectre électromagnétique.
-
Les phénomènes de
diffraction et d’interférences de la lumière s’expliquent par les propriétés
ondulatoires de la lumière.
-
En 1900, Max PLANCK
fut conduit à postuler la quantification de l’énergie transportée par les ondes
électromagnétiques.
-
Il postule que
l’énergie électromagnétique ne peut s’échanger que par « paquets » ou quanta
d’énergie.
-
En 1905, Albert
EINSTEIN émet l’idée que ces quanta d’énergie sont transportés par des
particules.
-
On parle de modèle
particulaire de la lumière.
-
En 1926, Gilbert
NEWTON invente le mot « photons pour nommer ces quanta.
-
Les photons sont
des particules de masse nulle et de charge nulle se propageant à la vitesse de
la lumière.
1)- Description de l’effet photoélectrique :
-
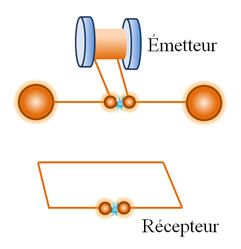
En 1887, le physicien
allemand H. HERTZ met au point un oscillateur hautes fréquences.
-
Grâce à des étincelles
produites entre deux petites sphères en laiton très proches, le dispositif émet
des ondes électromagnétiques.
-
H. HERTZ réceptionne à
quelques mètres de là ces ondes à l’aide d’un fil conducteur en forme de boucle
ou de rectangle ouvert avec également deux boules de laiton à chacune de ses
extrémités.
-
Il observe des
étincelles de faible intensité lumineuse entre les boules de laiton du
récepteur.
-
Cette expérience
couronne la théorie de l’Écossais J.C. MAXWELL établie en 1865 sur le
comportement ondulatoire des ondes électromagnétiques.
- Afin de mieux voir les étincelles au niveau du récepteur, H. HERTZ place le récepteur dans l’obscurité.
- Il constate alors que l’intensité lumineuse des étincelles est encore plus
faible.
-
Il en déduit que la
lumière émise par les étincelles de l’émetteur, plus précisément les
rayonnements ultraviolets, a un impact sur les étincelles du récepteur.
-
H. HERTZ vient de
mettre en évidence l’effet photoélectrique.
-
S’il identifie la
cause du phénomène observé, il ne sait pas l’interpréter.
-
Historique :
- Dans les années qui suivent l’expérience de H. HERTZ, différents travaux consistent à éclairer un métal par un rayonnement ultraviolet.
- On obtient les résultats suivants :
►
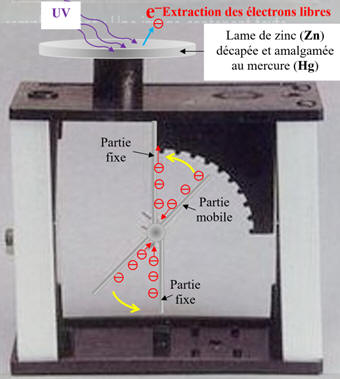
Expérience avec
l’électroscope :
-
On charge négativement un électroscope
sur lequel on a posé une lame de zinc (Zn)
décapée et amalgamée avec du mercure (Hg).

-
On éclaire la lame de zinc avec une
lampe U.V.
-
On remarque que l’électroscope se
décharge rapidement.
-
La lame de zinc, au départ, est chargé
négativement.
-
Elle possède un excès d’électrons.
-
Si elle se décharge, c’est que des
électrons ont été arrachés au métal
-
C’est l’effet photoélectrique.
-
L’énergie nécessaire à l’extraction des
électrons est fournie par la lampe UV.
►
Extraction des électrons :
- En 1888, Wilhelm HALLWACHS constate qu’une plaque de zinc éclairée par de la lumière ultraviolette se charge positivement.
- Il en conclue que les rayonnements
ultraviolets arrachent des particules négatives que l’on appellera des
électrons.
-
Entre 1889 et 1895,
Julius ELSTER et Hans GEITEL établissent un classement des métaux vis-à-vis de
ce phénomène.
- En 1900, Philipp LENARD montre que des particules négatives sont arrachées d’une plaque métallique sous l’effet de la lumière.
- Ces particules sont les électrons
découverts en 1897 par Joseph John THOMSON.
-
Le nombre d’électrons
arrachés est proportionnel à l’intensité lumineuse du rayonnement.
-
L’énergie cinétique
des électrons arrachés est indépendante de l’intensité lumineuse du rayonnement.
-
L’énergie cinétique
augmente lorsque la fréquence de la lumière incidente augmente.
-
Le modèle ondulatoire
de la lumière ne permet pas d’expliquer ces différentes observations.
-
En 1905, pour
expliquer l’effet photoélectrique, A. EINSTEIN propose un aspect particulaire
pour la lumière.
-
Chaque particule
possède une énergie : E
= h .
υ.
-
Cette particule sera
appelée photon quelques années plus tard.
-
A. EINSTEIN explique
que l’énergie du photon sert en partie à arracher l’électron de l’atome, le
reste étant emporté par l’électron sous forme d’énergie cinétique.
- Ce résultat sera démontré expérimentalement par le physicien américain R. MILLIKAN (1868–1953) onze ans plus tard
- et la communauté scientifique mettra quelques années de plus
à accepter la notion d’aspect particulaire de la lumière.
-
En
1921, A. EINSTEIN obtiendra le prix Nobel de physique pour cette découverte.
-
En 1926, Gilbert
NEWTON nomme « photons » les particules de lumière porteuses de ces quanta
d’énergie.
►
L’effet
photoélectrique :
-
C’est le phénomène
d’éjection d’électrons d’un métal sous l’effet de radiations lumineuses.
-
Pour un métal donné,
cet effet ne se manifeste que pour des photons d’énergie suffisamment grande.
-
L’effet est quasiment
instantané.
-
Il se
manifeste si l’énergie du photon est supérieure au travail d’extraction d’un
électron du métal Wextraction.
-
L’énergie excédentaire
est emportée par l’électron sous forme d’énergie cinétique.
-
Tableau de quelques
valeurs :
|
|
Matériau |
Travail
d’extraction
Wextraction |
|
Z
= 6 |
Carbone |
5,0 eV |
|
Z
= 11 |
Sodium |
2,7 eV |
|
Z
= 14 |
Silicium |
4,8 eV |
|
Z
= 29 |
Cuivre |
4,7 eV |
|
Z
= 30 |
Zinc |
3,6 eV |
|
Z
= 47 |
Argent |
4,3 eV |
|
Z
= 79 |
Or |
5,1 eV |
►
Le
photon :
-
La lumière peut être
décrite comme un flux de photons.
-
Un
photon possède une masse nulle et se propage à la célérité
c
de la lumière dans le vide.
|
c = 299 792
458 m . s–1 |
-
L’énergie de la
lumière est transportée par des photons qui présentent un aspect particulaire et
un aspect ondulatoire.
-
L’énergie d’un
photon est donnée par la relation :
-
E = h
.
n
-
L’énergie E
représente l’aspect particulaire du photon.
-
La fréquence
n
représente son aspect ondulatoire.
-
Pour une onde
électromagnétique de fréquence
n
et de longueur d’onde λ
dans le vide,
-
On peut écrire :
|
Relation de
PLANCK-EINSTEIN :
|
|
|
h |
La grandeur
h est la constante de Planck :
h
= 6,626 × 10–34 J . s |
|
υ |
La fréquence
υ
en hertz (Hz) |
|
λ |
La longueur
d’onde dans le vide λ en
mètre (m) |
|
c |
La célérité de la
lumière dans le vide :
c =
3,00 × 108 m . s – 1 |
|
E |
Énergie
E en joule (J) ou électronvolt (eV)
1 eV = 1,60 × 10–19
J |
-
Cette relation met
en évidence le caractère à la fois :
-
Particulaire :
photon, particule de masse nulle et d’énergie
Ephoton.
-
Ondulatoire :
fréquence ν,
longueur d’onde λ.
-
On parle de dualité
onde-corpuscule.
►
Remarque 1 :
-
Plus la longueur d’onde associée au
photon est grande est plus l’énergie qu’il transporte est petite.
-
Plus la longueur d’onde est grande et
plus la fréquence du photon est petite.
-
Plus la fréquence du photon est grande
et plus l’énergie associée au photon est grande.
►
Remarque 2 :
-
Pour un
métal donné, l’effet photoélectrique se produit lorsque la longueur d’onde de la
radiation mise en jeu est inférieure à une longueur d’onde de seuil
λS.
-
La fréquence
ν
de cette radiation est alors supérieure à la fréquence de seuil
νS.
- L’énergie de chaque photon associé à cette radiation lumineuse est alors suffisante pour arracher un électron du métal,
-
Elle est supérieure au travail d’extraction d’un
électron du métal Wextraction.
: On observe alors l’effet photoélectrique.
3)- Bilan énergétique et interprétation à l’aide du
modèle particulaire.
►
Le
métal solide :
-
Un métal solide est un
assemblage compact et ordonné d’atomes.
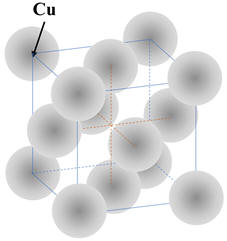
►
Exemple : cristal de cuivre :
-
Le cuivre cristallise
dans le système cubique à faces centrées.
-
Les atomes qui le
constituent sont proches les uns des autres.
-
Leurs électrons, et en
particulier les électrons périphériques, sont soumis à des interactions de la
part de tous les noyaux environnants.
-
Pour certains
électrons périphériques, les interactions avec les noyaux des atomes voisins
sont si fortes qu’ils sont libérés de leur atome initial :
-
Ce sont
les électrons
libres que l’on appelle aussi électrons de
conductions.
-
Ce sont ces électrons
qui assurent la cohésion du cristal.
-
Ils se dépassent dans
toutes les directions de façon désordonnée.
-
Un courant électrique
dans un métal est dû à un déplacement d’ensemble ordonnée de ces électrons
libres.
►
Travail d’extraction :
Wextraction.
-
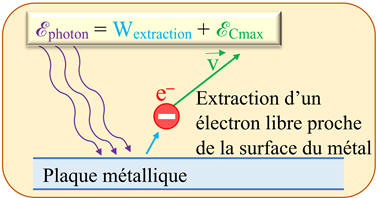
L’énergie minimale qui
permet d’arracher un électron d’un métal est égale au travail à fournir pour
extraire un électron libre proche de la surface du métal.
-
Cette
énergie est appelée travail d’extraction, notée
Wextraction.
-
Elle diffère d’un
métal à un autre. C’est une grandeur caractéristique d’un métal.
-
Si
l’énergie du photon est supérieure au travail d’extraction
Wextraction,
l’excédent d’énergie est emporté par cet électron sous forme d’énergie
cinétique.
-
L’arrachage d’autres
électrons nécessite une plus grande énergie.
-
Pour une même
radiation lumineuse, l’énergie de l’électron arraché est plus faible.
-
En conclusion :
-
L’énergie cinétique
d’un électron arraché est maximale pour un électron libre proche de la surface
du métal.
-
Schéma :
-
Équation de
conservation de l’énergie : Équation d’EINSTEIN de l’effet photoélectrique.
-
ℰphoton
= Wextraction +
ℰCmax
-
Avec :
-
ℰphoton
= h .
υphoton
et
- ![]()
-
Tableau :
|
ℰphoton = Wextraction
+ ℰCmax
|
|
|
υphoton |
La fréquence du
photon en hertz (Hz) |
|
Wextraction |
Travail
d’extraction en joule (J) ou électron-volt (eV)
1 eV = 1,60 × 10–19
J |
|
me |
Masse de
l’électron : me = 9,109 × 10–31 kg |
|
vmax |
Vitesse maximale
de l’électron
en mètre par
seconde (m . s–1) |
|
h |
Constante de
Planck :
h
= 6,626 × 10–34 J . s |
-
Énergie cinétique
maximale des électrons en fonction de la fréquence
υphoton
du photon incident :
-
Cas du potassium et du
béryllium :
-
On
remarque que lors de l’effet photoélectrique, l’énergie cinétique maximale ℰCmax
augmente avec la fréquence
υ des photons incidents.
-
Le
coefficient directeur a de chaque droite permet de
retrouver la constante de Planck
h.
-
a
= h
-
L’équation d’EINSTEIN
de l’effet photoélectrique explique chaque aspect de l’effet photoélectrique
comme l’augmentation de l’énergie cinétique maximale des électrons arrachés en
fonction de la fréquence du photon incident.
-
Si la lumière
apportait progressivement l’énergie nécessaire pour l’extraction des électrons
du métal, comme le prévoir la théorie ondulatoire, il faudrait éclairer le métal
pendant une durée suffisante pour y parvenir.
-
Or pour que le
phénomène ait lieu, il faut que l’énergie apportée par le photon soit
suffisante.
-
-
Lorsque l’énergie
apportée par le photon est suffisante, le phénomène a lieu quasi instantanément.
-
Si l’énergie apportée
par le photon incident est insuffisante alors le phénomène n’a pas lieu.
►
En
conclusion :
-
Pour
que l’effet photoélectrique se produise, il faut que la fréquence des électrons
soit supérieure la fréquence seuil
υS.
-
Comme 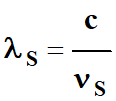
-
Il faut
que la longueur d’onde λ, du photon incident, soit inférieure à la longueur d’onde seuil
λS.
-
C’est la longueur
d’onde maximale au-delà de laquelle il n’est pas possible d’arracher les
électrons libres du métal.
-
Si λ
> λS.
alors υ
< υS
et l’énergie transportée par le photon (E
= h .
υ
< h
. υS)
est inférieure à l’énergie minimale permettant d’arracher un électron libre à la
surface du métal.
►
Modèle particulaire de la lumière :
-
La lumière est un flux
de photons.
-
Cette description
permet d’expliquer l’effet photoélectrique que l’on ne peut pas expliquer par le
phénomène ondulatoire.
-
La lumière présente
une dualité onde-corpuscule.
-
La lumière peut être
décrite de manière :
-
Corpusculaire par la
propagation de photons.
-
Ondulatoire par la
propagation d’une onde électromagnétique.
III-
L’absorption ou l’émission
de photons.
1)- Émission et absorption de photons.
►
Émission d’un photon par un atome.
-
Dans ce cas,
Einitial >
Efinal
-
L’atome perd de
l’énergie en émettant un photon.
-
Sur un diagramme
d’énergie, on représente cette transition par une
flèche verticale
orienté vers le bas.
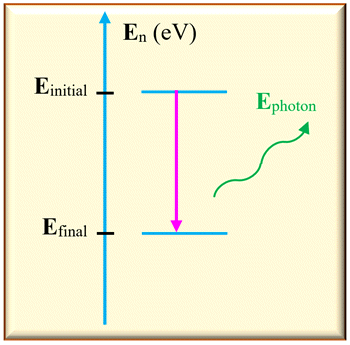
-
L’énergie libérée
est égale à la différence d’énergie entre les deux niveaux :
-
ΔE
= | Efinal –
Einitial
|
-
Cette énergie est
transportée par un photon :
-
Ephoton =
ΔE = |
Efinal
–
Einitial | =
h .
ν
-
La fréquence
ν
découle de la différence d’énergie
ΔE
= | Efinal –
Einitial
|
-
Si cette fréquence
appartient au domaine du visible, elle correspond alors à une raie colorée dans
le spectre d’émission de l’atome.
►
Absorption d’un photon par un atome.
-
Dans ce cas,
Einitial <
Efinal
-
L’atome gagne de
l’énergie en absorbant un photon.
-
Sur un diagramme
d’énergie, on représente cette transition par une
flèche verticale
orienté vers le haut.
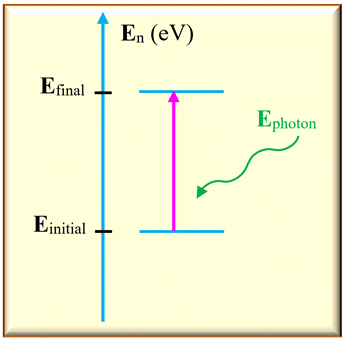
-
L’énergie absorbée
est égale à la différence d’énergie entre les deux niveaux :
-
ΔE
= | Efinal –
Einitial
|
-
Cette énergie est
transportée par un photon :
-
Ephoton =
ΔE = |
Efinal
–
Einitial | =
h .
ν
-
La fréquence
ν
découle de la différence d’énergie
ΔE
= | Efinal –
Einitial
|
-
L’absorption
d’énergie lumineuse par un atome ne peut se faire que si l’énergie du photon
permet une transition d’un niveau
Einitial à un niveau supérieur
Efinal
tel que :
-
Efinal –
Einitial
=
h
. ν
-
Si cette fréquence
ν
appartient au domaine du visible, elle correspond alors à une raie noire dans le
spectre de la lumière blanche.
►
Exemple spectre d’émission et d’absorption de l’atome de sodium :
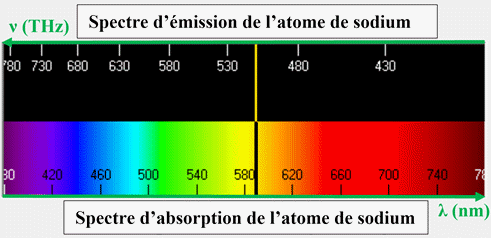
►
En conclusion :
-
Chaque entité
chimique possède son propre diagramme d’énergie.
-
Il est ainsi
possible d’identifier une entité chimique (atome, molécule ou ion) à partir de
son spectre d’émission ou d’absorption.
-
Les radiations
émises ou absorbées sont caractéristiques d’un atome car elles dépendent des
niveaux d’énergie de cet atome.
2)- Absorption de photons et cellule photoélectrique.
►
Cellule photoélectrique :
-
Une cellule
photoélectrique est formée d’une ampoule où règne le vide, qui comprend :
-
Une photocathode
susceptible de subir l’effet photoélectrique,
-
Une anode dont le rôle
est d’accélérer et de collecter les électrons émis grâce à un rayonnement.
-
Photo :

-
Représentation
symbolique :
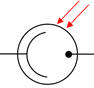
-
Schéma :
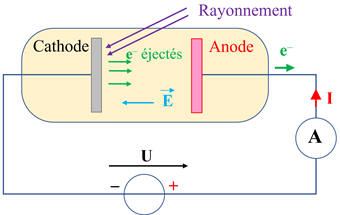
-
La
tension U
appliquée entre la cathode et l’anode permet d’accélérer les électrons éjectés
grâce au rayonnement qui possède la fréquence adaptée.
-
Les électrons éjectés
sont soumis à la force électrique :
- ![]()
-
Plus généralement, une
cellule photoélectrique est un dispositif dont une propriété électrique est
modifiée lors de l’absorption de photons.
-
On utilise des
matériaux semi-conducteurs pour réaliser des cellules photoélectriques.
►
La cellule photovoltaïque :
-
Les cellules
photovoltaïques exploitent l’effet photoélectrique pour produire un courant
continu par absorption d’un rayonnement solaire.
-
Une telle cellule
convertit directement l’énergie lumineuse des photons en énergie électrique.
-
Pour fabriquer de
telles cellules, on utilise des semi-conducteurs.
►
Principe de fonctionnement :
-
Une cellule
photovoltaïque est composée de 2 types de matériaux semi-conducteurs :
-
L’un
des matériaux présente un excès d’électrons, elle est dite dopée de type
n
(comme négatif)
-
et
l’autre un défaut d’électrons, elle est dite dopée de type
p
(comme positif)
-
Exemple :
-
Un
atome de silicium, Si (Z
= 14), possède 4 électrons sur sa couche électronique externe (…3s23p2)
-
L’une des couches de
la cellule est dopée avec des atomes de phosphore,
-
L’atome
de phosphore, P (Z = 15), possède 5 électrons
sur sa couche électronique externe (…3s23p3).
-
Il possède donc 1
électron de plus que l’atome de silicium.
-
On dit
que cette couche a subi un dopage de type
n
(elle présente un excès d’électrons)
-
L’autre couche est
dopée avec des atomes de bore,
-
L’atome de bore,
B (Z
= 5), possède 3 électrons sur sa couche électronique externe (…2s22p1).
-
On dit
que cette couche a subi un dopage de type
p
(elle présente un défaut d’électrons)
-
Lorsque
la première couche est mise en contact avec la seconde, les électrons en excès
dans le matériau dopé
n diffusent dans le matériau dopé
p.
-
Lorsque des photons
percutent un semi-conducteur comme le silicium, ils arrachent des électrons et
créent ainsi des trous positifs dans le semi-conducteur.
-
Les trous positifs
ainsi créés sont comblés par d’autres électrons qui créent eux aussi des trous
positifs et ainsi de suite.
-
Les autres électrons
se mettent en mouvement, de façon désordonnée, à la recherche d’autres trous
positifs où se repositionner.
-
Il se crée un
mouvement d’électrons et de trous positifs de façon désordonnée.
-
Pour créer un courant
électrique, il faut que tous les électrons se déplacent dans le même sens de
façon ordonnée.
-
Pour
réaliser ce phénomène, la face exposée au Soleil de la cellule photovoltaïque
est dopée avec des atomes de phosphore
P
et l’autre face est dopée avec des atomes de bore
B.
-
Ce système constitué
des deux couches se comporte comme une pile :
-
Le côté
dopé de type n devient la borne négative (N)
-
L’autre
côté dopé de type p devient la borne positive (P)
-
Entre les deux couches
se crée un champ électrique ![]()
-
Sous
l’effet des photons, les électrons vont migrer vers la couche
N
sous l’effet du champ électrique
![]() alors
que les trous positifs vont migrer vers la couche
P.
alors
que les trous positifs vont migrer vers la couche
P.
-
Les électrons sont
récupérés par des contacts électriques déposés à la surface des deux zones afin
d’aller vers le circuit extérieur sous forme d’énergie électrique.
-
Un courant électrique
est ainsi créé.
-
Il est dû à la double
migration des électrons et des trous positifs se déplaçant en sens inverse.
-
Schéma :
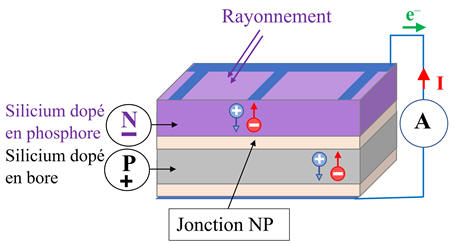
Ou
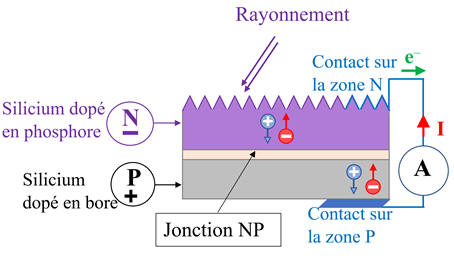
-
Représentation
symbolique d’une cellule photovoltaïque :
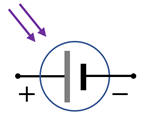

►
Rendement
d’une cellule photovoltaïque :
-
Le
rendement η d’une cellule photovoltaïque
est le rapport de la puissance exploitable sur la puissance en entrée.
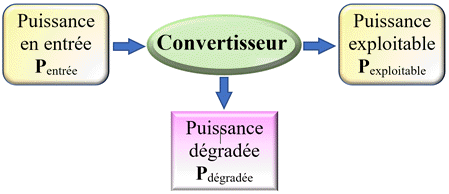
|
|
η
sans unité |
|
Pexploitable
en watt (W) |
|
|
Pentrée
en watt (W) |
ou
-
Le
rendement η d’une cellule photovoltaïque
est le rapport de l’énergie exploitable sur l’énergie en entrée.
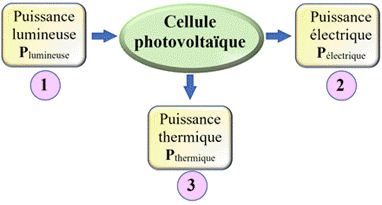
-
Avec les notations
précédentes :
|
|
|
|
η |
Grandeur sans
unité : 0 < η ≤ 1 |
|
Pélectrique |
Puissance
exploitable : Puissance électrique en watt (W) |
|
Plumineuse |
Puissance en
entrée : Puissance lumineuse en watt (W) |
-
On peut aussi utiliser
les énergies :
|
|
|
|
η |
Grandeur sans
unité : 0 < η ≤ 1 |
|
ℰélectrique |
Énergie
exploitable : Énergie électrique en joule (J) |
|
ℰlumineuse |
Énergie en
entrée : Énergie lumineuse en joule (J) |
-
Le rendement des
cellules photovoltaïques est faible, de l’ordre de 10 %, mais l’énergie
lumineuse est inépuisable à notre échelle.
►
Autres cellules
photoélectriques :
-
La photorésistance :
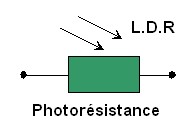

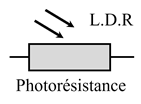
-
Une
photorésistance (LDR :
Light Dependent Resistor)
est un composant électronique dont la résistance varie en fonctionne de la
quantité de lumière reçue.
-
La résistance de ce
dipôle diminue d’autant plus que la lumière qu’il reçoit est intense.
-
Photodiode :
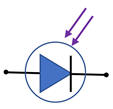

-
C’est un dipôle dont
l’intensité qui le traverse est d’autant plus grande que la lumière qu’il reçoit
est intense.
-
Dans l’obscurité, la
caractéristique de la photodiode est identique à celle d’une diode ordinaire.
-
En pleine lumière,
elle conduit le courant en sens inverse.
-
L’intensité du courant
inverse dépend de l’éclairement.
-
Si l’éclairement
augmente, l’intensité du courant inverse augmente en valeur absolue.
-
Une information
lumineuse peut être convertie en un signal électrique grâce à une photodiode.
-
L’intensité du courant
dépend également de la longueur d’onde de la lumière reçue.
-
Les photodiodes sont
utilisées dans les capteurs CCD ou CMOS que l’on trouve dans les capteurs des
appareils photographiques.

3)- Émission de photons et diodes électroluminescentes
(DEL).
-
Une diode
électroluminescente (DEL) est un dipôle dont le passage du courant électrique
dans sa structure semi-conductrice entraîne l’émission de photons.
-
C’est un dipôle
optoélectronique
-
Elle utilise le
phénomène de l'électroluminescence.
-
La fréquence de la
lumière émise dépend de la nature du semi-conducteur utilisé.
-
Représentation
symbolique :
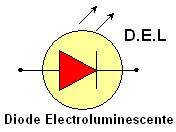

-
Les DEL font partie
des dispositifs d’éclairage les plus performants du point de vue énergétique.
-
Contrairement aux
ampoules à incandescence, la DEL ne possède pas de filament.
-
Elles convertissent
très peu d’électricité en quantité de chaleur.
-
Le rendement d’une DEL
est voisin de 50 %.
-
C’est un composant qui
est de plus en plus utilisé dans différents domaines :
-
L’éclairage, les
téléviseurs, les écrans d’ordinateurs, ….
1)- Rendement d’une cellule photovoltaïque.

|
QCM r
La lumière : un flux
de photons Effet photoélectrique L’absorption ou
l’émission de photons |
|
Exercices : énoncé avec correction. DS 1)- Exercice 03 page 416 : Connaître l’effet
photoélectrique. 2)- Exercice 05 Page 416 : Interpréter l’effet
photoélectrique. 3)- Exercice 07 page 416 : Réaliser un bilan
d’énergie. 4)- Exercice 09 page 417 : Calculer des rendements. 5)- Exercice 13 page 417 : Conservation de
l’énergie. 6)- Exercice 15 page 418 : Énergie cinétique des
électrons. 7)- Exercice 17 page 419 : Comparaison de
l’effet photovolaïque. 8)- DS 01 : Effet photovoltaïque et panneaux
photovoltaïques (60 min) 9)- Préparation à l’ECE : Rendement d’une
cellule photovoltaïque. |
|
|