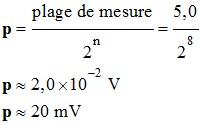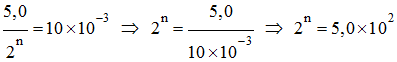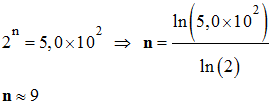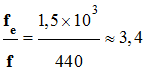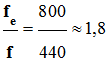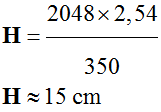|
Chap. N° 20 |
Numérisation de l'information. Exercices |
|
|
|
|
QCM réalisé avec le
logiciel Questy |
I-
Exercice 9 page 530 : Calculer une fréquence
d’échantillonnage.
|
Un signal sonore converti en
signal numérique est représenté ci-dessous : 1)- Déterminer la fréquence f du signal
sonore étudié. 2)- Échantillonnage : a)- b)- c)- |
|
1)- Fréquence f du signal sonore étudié :
-
Valeur de la période T : -
-
Fréquence du signal : -
2)- Échantillonnage : a)- -
La fréquence d’échantillonnage fe
représente de nombre d’échantillons prélevés par
seconde. b)- -
Pour une période T= 4,66 ms, on
dénombre 23 points : -
-
Comparaison : -
-
La fréquence d’échantillonnage est 23
fois plus élevée que la fréquence du signal sonore. c)- -
Si la fréquence d’échantillonnage
augmente, le rapport
-
Le nombre de valeurs de l’échantillon
prélevé est plus grand. -
Le signal numérisé est d’autant plus
proche du signal analogique que : -
La fréquence d’échantillonnage est
grande, la durée entre deux mesures est alors plus
faible : quand fe ↑, alors Te
↓. |
II- Exercice N° 13 page 530 : Associer un tableau de nombres
à une image numérique.
|
Le document ci-dessous
correspond à l’image agrandie et pixellisée de la
photographie située en haut à droite : Les tableaux ci-dessous (A, B
et C) correspondent au codage de trois zones (1, 2
et 3) repérées sur l’image.
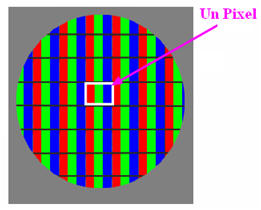
1)- Le pixel : a)-
Qu’est-ce qu’un pixel. b)-
Comment apparaît un pixel sur l’image ? c)-
Qu’observerait-on si l’image était encore
agrandie ? 2)- Quelle est la couleur dominante des zones 1,
2 et 3 sélectionnées ? 3)- Attribuer un tableau de nombres (A),
(B) ou (C) à chacune des zones
sélectionnées, en justifiant. |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
1)- Le pixel : a)-
Définition du pixel. -
Le pixel est la plus petite unité
lumineuse d’une image. -
Un pixel est constitué de trois
sous-pixels. -
Chaque pixel est constitué de trois
sous-pixels : trois luminophores -
Un sous-pixel qui diffuse de la
lumière rouge. -
Un sous-pixel qui diffuse de la
lumière verte. -
Un sous-pixel qui diffuse de la
lumière bleue. b)-
Le pixel sur l’image : -
Un pixel est représenté par un carré
sur l’image.
c)-
Image agrandie : - Lorsque l’on agrandie l’image, la taille du pixel augmente. -
L’image est pixellisée. 2)- Quelle est la couleur dominante des zones 1,
2 et 3 sélectionnées ? -
Zone 1 : -
Zone 2 :
-
Zone 3 : 3)- Tableau de nombres (A), (B) ou
(C) et zones sélectionnées 1, 2 et 3. -
Couleur et tableau de nombres : -
Un tableau correspond au codage
RVB
de chaque pixel. -
On utilise le principe de la
trichromie et de la synthèse additive des couleurs. -
Le tableau (A) :
-
Les nombres associés aux sous-pixels
verts sont les plus grands. -
La couleur qui prédomine est le vert. -
Le tableau (A) correspond à la
zone 3 -
Le tableau (B) :
-
Les nombres associés aux sous-pixels
sont du même ordre de grandeur, elles sont proches :
R 347,
V243 et
B 242). - Aucune couleur ne prédomine. -
La
couleur associée à ce tableau est le blanc. -
Le tableau (B) correspond à la
zone 2
-
Tableau (C) :
-
Les nombres associés aux sous-pixels
rouges sont les plus grands. -
La couleur qui prédomine est le rouge. -
Le tableau (C) correspond à la
zone 1 |
||||||||||||||||||||||||||||||||||||||||||||||||
III- Exercice 15 page 531 : échantillonnage et CD.
|
Afin de pouvoir restituer
correctement un son, la fréquence d’échantillonnage
doit être au moins le double de la fréquence de
l’harmonique le plus haut de ce son. La fréquence d’un son audible
par l’oreille humaine est comprise entre 20 Hz et 20
kHz. 1)- Quelle fréquence d’échantillonnage minimale
faut-il choisir pour numériser correctement un son ? 2)- La fréquence d’échantillonnage standard pour les CD est de 44,1 kHz. Cette valeur est-elle en
accord avec le résultat de la question précédente ? 3)- Les standards d’enregistrement sur CD codent les sons en 16 bits. Combien de niveaux d’intensité
sonore différents peut-on coder ? 4)- Quelle est la durée maximale
d’enregistrement disponible sur un CD dont la
capacité de stockage est de 700 Mio ? (1 Mio = 220
octets) |
|
1)- Fréquence d’échantillonnage minimale pour
numériser correctement un son : -
La fréquence d’échantillonnage
minimale est le double de la plus haute fréquence
audible par une oreille humaine : -
fe = 2 f = 40
kHz 2)- Fréquence d’échantillonnage :
-
La valeur de la fréquence
d’échantillonnage des CD est : f’e
= 44,1 kHz. -
f’e > fe -
Cette valeur est en accord avec le
résultat de la question 1. 3)- Nombre de niveaux d’intensité sonore
différents en codage 16 bits : -
Le signal est codé en 16 bits : -
Le nombre de valeurs possibles est : 216
= 65 536. 4)- Durée maximale d’enregistrement disponible
sur un CD dont la capacité de stockage est de 700
Mio : (1 Mio = 220 octets) -
Signal sonore échantillonné en qualité
CD : 44,1 kHz, 16 bits. -
On considère un signal stéréo (2
voies) -
Chaque seconde : 2
× 16
× 44,1
×103 bits = 1,41 Mbits -
Valeur en octet : 1 octet = 8 bits
-
Pour une seconde de son échantillonné
à 44,1 kHz : 176 ko. -
700 Mio = 700
× 220 = 734 Mo -
Durée maximale : - -
Pour un enregistrement stéréo. -
Ou 2 h 19 min pour un enregistrement
mono. |
IV- Exercice 16 page 531 : Acquisition d’une carte
d’acquisition.
|
Pour l’équipement des salles de physique du lycée, on a besoin de mesurer des tensions allant de 0 à 4,5 V à 10 mV près. Une carte
d’acquisition trouvée dans le commerce contient un
CAN 8 bits et a pour calibre 0,0 – 5,0 V. 1)- Déterminer le pas p du convertisseur
de ce modèle. 2)- Ce modèle correspond-il aux besoins du
lycée ? 3)- Quel doit-être le minimum de bits du CAN
pour que sa précision soit suffisante ? Donnée :
Coup de pouce : |
|
4)- Pas p du convertisseur de ce modèle : -
5)- Ce modèle correspond-il aux besoins du
lycée ? -
Ce modèle ne convient pas car il faut
une résolution de 10 mV. - Pour une séance de TP, la précision n’est pas suffisante. -
La résolution du convertisseur
CAN est de 20 mV. 6)- Nombre minimum de bits du CAN pour que sa
précision soit suffisante : -
La résolution doit être inférieure ou
égale à 10 mV. -
On connait la page de valeur : 5,0 V -
On choisit un pas p ≤ 10 mV et
n représente le nombre de bits. -
On doit résoudre :
-
-
On utilise la relation : -
-
Le convertisseur CAN doit comporter au
moins 9 bits. |
V- Exercice 20 page 532 : Le réseau téléphonique.
|
De nombreuse communications transitent par le réseau téléphonique. Ce dernier étant majoritairement numérisé, les centraux téléphoniques n’échangent plus un signal électrique engendré par la parole, mais des échanges de ce
signal prélevés 8000 fois par seconde. Chaque échantillon est ensuite
codé sur 8 bits. 1)- Rappeler les principales étapes de la
numérisation d’un signal. 2)- Déterminer la fréquence d’échantillonnage
utilisée par les centraux téléphoniques. 3)- Combien de niveaux d’intensité sonore
peut-on obtenir avec le codage proposé ? 4)- Combien d’informations une ligne téléphonique doit-elle transporter par seconde pour transmettre la parole d’un usager ? Le résultat sera
donné en kibibit par seconde (Kibit . s–1) Donnée : 1 Kibit
= 210 bits. |
|
1)- Les principales étapes de la numérisation
d’un signal. -
Il désigne le procédé qui permet de
passer d’un signal analogique à un signal numérique. -
Les étapes principales de toute
conversion analogique-numérique sont : -
L’échantillonnage, -
La quantification, -
Et le codage.
► L’échantillonnage : - Le convertisseur analogique-numérique prélève des échantillons du signal analogique à intervalles de temps Te égaux appelés période d’échantillonnage. -
La fréquence d’échantillonnage fe
est le nombre de prélèvements effectués par seconde
(nombre de mesures effectuées par seconde). -
Elle définit le nombre de valeurs
prélevées au signal analogique par seconde.
► La quantification : -
L’échantillonnage consiste à prélever
certaines valeurs d’une fonction continue. -
On ne va retenir que les valeurs selon
un certain pas p de quantification. -
La quantification consiste à affecter
une valeur numérique à chaque échantillon prélevé. -
Chaque valeur est arrondie à la valeur
permise la plus proche par défaut.
► Le codage : -
La valeur permise est codée par un
nombre binaire. -
Les valeurs numérisées vont être
stockées sous forme de bits. - La qualité de la conversion analogique-numérique, ou numérisation, est d’autant plus grande que le pas p du convertisseur est petit et que la fréquence fe
d’échantillonnage est élevée. 2)- Fréquence d’échantillonnage utilisée par les
centraux téléphoniques. -
Prélèvement du signal : 8000 fois par
seconde. -
fe = 8,0
x 103 Hz 3)- Nombre de niveaux d’intensité sonore obtenu
avec le codage proposé : -
Chaque échantillon est codé à 8 bits : -
Le nombre de valeurs prélevées est : 28
= 256. 4)- Nombre N d’informations transportées
par seconde : -
Signal sonore échantillonné à une
fréquence de 8,0 kHz et de codage 8 bits : -
N = 8
x 8000 -
N = 64 kbits / s -
Avec : 1 Kibit = 210 bits -
|
VI- Exercice 24 pages 533 et 534 : Critère de Shannon et
théorie de l’échantillonnage.
|
Un instrument de musique joue un La1 de fréquence f1 = 110 Hz. On réalise quatre numérisations (A, B, C
et D) en changeant uniquement la fréquence
d’échantillonnage fe. Les spectres en fréquence
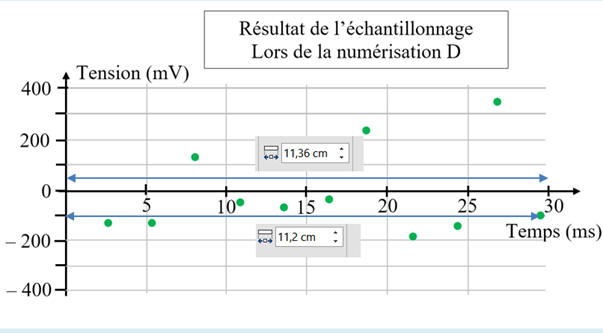
obtenus sont représentés ci-dessous. Le dernier graphe montre le
résultat de l’échantillonnage lors de la
numérisation D. D’après le critère de Shannon, la fréquence d’échantillonnage doit être au moins deux fois égale à la fréquence de l’harmonique de
rang le plus élevé contenu dans le son à numériser
pour ne pas altérer le signal. On considère que la
numérisation A est très fidèle au son émis par
l’instrument. 1)- Quelle est la fréquence d’échantillonnage
utilisée lors de la numérisation D. 2)- Quelle est la fréquence f de
l’harmonique de rang le plus élevé contenu dans la
note La1 joué par cet instrument ? 3)- Fréquence d’échantillonnage. a)-
Comparer la fréquence d’échantillonnage à
f pour cette numérisation. b)-
Le critère de Shannon est-il vérifié ? 4)- Est-il nécessaire d’augmenter indéfiniment
la fréquence d’échantillonnage pour améliorer la
numérisation du son ? |
|
1)- Fréquence d’échantillonnage utilisée lors de
la numérisation D. -
Exploitation du graphe : -
Tableau :
-
La période d’échantillonnage
-
-
La fréquence d’échantillonnage de la
numérisation D : -
2)- Fréquence f de l’harmonique de rang
le plus élevé contenu dans la note La1
joué par cet instrument : -
La fréquence f de l’harmonique
de rang le plus élevé : -
D’après l’exploitation des spectres A
et B : -
f = 4 f1 =
440 Hz 3)- Fréquence d’échantillonnage. a)-
Comparaison de la fréquence d’échantillonnage
à f pour cette numérisation. -
Numérisation A : -
-
On remarque que f > 2 fe.
Le signal sonore sera bien restitué. -
Numérisation B : -
-
On remarque que f > 2 fe.
Le signal sonore sera bien restitué. -
Numérisation C : -
- On remarque que f < 2 fe. Le signal sonore ne sera pas bien restitué. - Il subit des altérations. - Il apparaît des fréquences parasites. -
L’harmonique la plus élevée perd de
l’amplitude, alors que l’harmonique 3 f = 330
Hz a une amplitude plus grande.
-
Numérisation
D : -
- On remarque que f < fe. -
Le signal sera très mal restitué. b)- Le critère de Shannon est-il vérifié ?
-
Le critère de Shannon n’est pas
vérifié. 4)- Est-il nécessaire d’augmenter indéfiniment
la fréquence d’échantillonnage pour améliorer la
numérisation du son ? -
Le critère de Shannon est vérifié pour
les numérisations A et B. - On remarque que les deux spectres en fréquences A et B sont identiques. -
Dans les deux
cas, le son sera fidèle au son émis. -
Pourtant, feB < feA. - Dans le cas présent, il n’est pas nécessaire de prendre une fréquence d’échantillonnage très élevée. -
La qualité de la
numérisation ne sera pas meilleure. -
Le critère de Shannon n’est pas
vérifié pour les numérisations C et
D. -
Dans ces deux cas la qualité de la
numérisation est mauvaise et le signal ne sera pas
fidèle au son émis. - Il n’est pas nécessaire d’augmenter indéfiniment la fréquence d’échantillonnage puisque l’oreille humaine ne peut déceler les fréquences des
harmoniques supérieures à 20 kHz. -
Dans le cas présent une fréquence
d’échantillonnage fe = 1,5 kHz
suffit. -
Car au plus la fréquence
d’échantillonnage est élevée, au plus la taille du
fichier sera grande. -
Il faut prendre la fréquence
d’échantillonnage suffisante pour avoir une bonne
numérisation et un fichier de taille acceptable. |
VII- Exercice 30 page 537 : Appareil photo numérique.
|
La notice d’un appareil
photographique numérique indique une « résolution »
du capteur CCD de 3072
x 2048, soit 6,3 mégapixels (Mpx). Une image est dite de qualité « photo » quand la taille du pixel est suffisamment petite pour qu’un œil normal n’en perçoive pas les détails. On considère qu’un œil normal peut percevoir des détails lorsque les rayons lumineux issus de ces détails arrivent dans l’œil avec un
angle supérieur à une minute. En codage normal, un pixel est
codé en RVB 24 bits. Données : 1 Mio = 1024 Kio et 1 Kio =
1024 octets 1 pouce = 2,54 cm
1)- Image numérique : a)-
Qu’appelle-t-on image numérique ? b)-
Par abus de langage, les fabricants utilisent
le terme « résolution ». Quel est celui qui convient
en réalité ? c)-
Le constructeur affiche une « résolution » de
3072
x 2048. Que représente ces valeurs ? 2)- Mio et octets : a)-
Combien d’octets sont utilisés pour coder un
pixel. b)-
Déterminer la taille d’une image
correspondant à la « résolution » indiquée par le
fabricant. Exprimer le résultat en Mio. 3)- Calculer la taille du plus petit détail que
l’on peut observer à l’œil nu sur un objet situé à
25 cm de l’œil. 4)- Résolution et photo : a)- Quelle est la résolution minimale d’une image numérique de qualité photo située à une distance de 25 cm de l’œil ? On exprimera la résolution en ppp :
pixels par pouce. b)- On souhaite imprimer une photo prise avec cet appareil. Quelle est la taille maximale de
l’impression qui permet d’avoir une qualité photo ?
On l’exprimera en cm
x cm. |
|
1)- Image numérique : a)-
Image numérique : -
Une image numérique est composée de
pixels, eux-mêmes divisés en trois sous-pixels. -
En codage
RVB
24 bits ou 3 octets,
chaque sous-pixels
peut prendre 256 nuances. -
On a pour un pixel : 256
x 256
x 256 couleurs, soit environ 16 millions. -
Une image numérique est codée par un
tableau de nombre. -
Chaque pixel de l’image numérique est
codé par 3 nombres.
-
En codage
RVB
24 bits, il est possible de réaliser 256 nuances de
gris en affectant la même valeur à chaque
sous-pixel : -
En partant du noir
R(0)V(0)B(0)
au blanc R(255)V(255)B(255) b)- Le terme « résolution ».
-
La définition d’une image numérique
correspond au nombre de pixels qui constituent cette
image. -
Le terme « résolution » peut être
remplacé par définition. c)- Le constructeur affiche une « résolution » de
3072
x 2048. -
Les valeurs 3072
× 2048 désignent le nombre de colonnes et le
nombre de lignes : -
Si une image est constituée de 3072
colonnes et de 2048 lignes, sa définition est égale
à : -
3072
× 2048 = 6 291 456 pixels. -
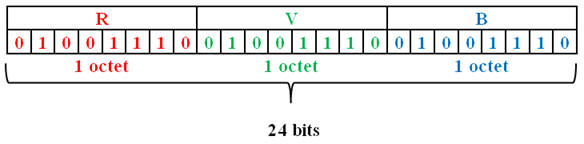
Soit environ 6,3 Mpx. 2)- Mio et octets : a)- Codage d’un pixel : -
En codage normal, un pixel est codé en
RVB 24 bits. -
Chaque pixel est constitué de trois
sous-pixels : -
Un sous-pixel qui diffuse de la
lumière rouge. -
Un sous-pixel qui diffuse de la
lumière verte. -
Un sous-pixel qui diffuse de la
lumière bleue. -
Chaque sous-pixel est codé sur un
octet, constitué par une séquence de huit bits : -
Un pixel est codé par 3 octets de 8
bits chacun. b)- -
La taille d’une image numérique est la
place qu’occupe le codage de tous les pixels qui
constituent cette image. -
La taille s’exprime en octet. -
Elle est donnée par la relation : -
taille = (nombre d’octets
par pixel)
x (définition) -
taille = 3
× 3072
× 2048 -
taille ≈ 18,9
× 106 octets = 18,9 Mo -
Résultat en Mio : 1 Mio = 1024 Kio et
1 Kio = 1024 octets -
-
18,9
× 106 octets ≈ 18,4
× 106 Kio -
-
18,4
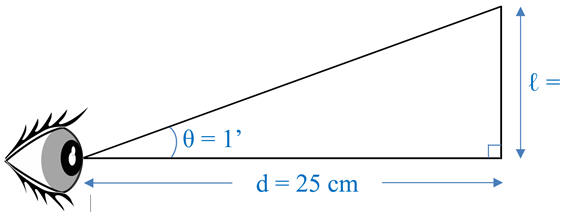
× 106 Kio ≈ 18 Mio 3)- Taille du plus petit détail que l’on peut
observer à l’œil nu sur un objet situé à 25 cm de
l’œil. -
Schéma de la situation : -
ℓ = d tan
θ -
4)- Résolution et photo : a)-
Résolution minimale d’une image numérique de
qualité photo située à une distance de 25 cm de
l’œil : -
La taille d’un pixel doit être
inférieur ou égale à 73 μm. -
Nombre minimum de pixels par pouce : -
b)-
Taille maximale de l’impression qui permet
d’avoir une qualité photo : -
On considère qu’au minimum, on observe
l’image à 25 cm d’un œil normal. -
Il faut au minimum 350 pixels par
pouce soit 2,54 cm. -
L’image a les caractéristiques
suivantes : 3072
x 2048 : -
Largeur de l’image en centimètres : -
-
Hauteur de l’image : -
-
Dimensions maximales de l’image situé
à 25 cm d’un œil normal : -
22 cm
x 15 cm. |
|
|








 La couleur dominante est le
rouge.
La couleur dominante est le
rouge. La couleur dominante est le
blanc.
La couleur dominante est le
blanc. La couleur dominante est le
vert.
La couleur dominante est le
vert.
 , avec n le nombre de
bits du convertisseur.
, avec n le nombre de
bits du convertisseur.