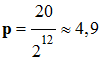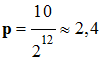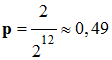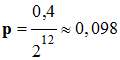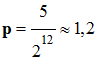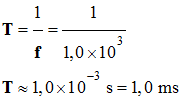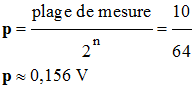|
Chap. N° 20 |
Numérisation de l'information. Cours |
|
|
|
|
QCM réalisé avec le
logiciel Questy |
|
Exercices (énoncé et corection)
a)-
Exercice 8 page 529 : Définir un signal numérique.
b)-
Exercice 9 page 530 :
Calculer une
fréquence d’échantillonnage.
c)-
Exercice N° 13 page 530 :
Associer un
tableau de nombres à une image numérique.
d)-
Exercice 15 page 531 : échantillonnage et CD.
e)-
Exercice 16 page 531 :
Acquisition d’une
carte d’acquisition.
f)-
Exercice 20 page 532 : Le réseau téléphonique.
g)-
Exercice 24 pages 533 et 534 :
Critère de
Shannon et théorie de l’échantillonnage.
h)-
Exercice 30 page 537 : Appareil photo numérique. |
I- Transmission des informations.
1)- La
chaîne de transmission d’informations.
-
La chaîne de transmission
d’informations est l’ensemble des éléments permettant de
transférer de l’information d’un lieu à un autre.
-
On désigne par canal de
transmission le dispositif par lequel les informations sont
transmises de l’émetteur à récepteur.
b)- Schématisation d’une chaîne de
transmission :
-
Une chaîne de transmission
d’informations comprend :
-
Un encodeur ;
-
Un canal de transmission composé
d’un émetteur, d’un récepteur, du milieu de transmission et de
l’information transmise ;
-
Un décodeur.
► Exemples de milieux de
transmissions :
-
L’atmosphère, les câbles
électriques, les fibres optiques.
-
Dans l’atmosphère, l’information
peut être transmise sous forme d’ondes ultrasonores, d’ondes
électromagnétiques.
-
Dans les câbles électriques,
l’information peut être transmise sous forme de signaux
électriques.
-
Dans la fibre optique,
l’information est transmise sous forme d’ondes
électromagnétiques (lumière visible, IR).
-
Schéma :

2)-
Évolution des chaînes de transmission d’informations.
-
Les évolutions techniques
importantes :
-
Passage de l’électricité à
l’électronique : miniaturisation des dispositifs.
-
Développement de l’informatique :
codage de tous les types d’information (sonore, vidéo, texte)
-
Passage du fil de cuivre à la
fibre optique : amélioration de la qualité, du débit des
transmissions.
-
La téléphonie mobile, le Wi-Fi,
le Bluetooth ont permis de s’affranchir des liaisons filaires.
► Quel canal de transmission
utilise-t-on pour la téléphonie filaire ?
- On utilise des câbles coaxiaux.
- Ces câbles relient les téléphones qui sont à la fois émetteurs et récepteurs.
- Dans les câbles circulent des signaux
électriques.
- On peut aussi utiliser la fibre optique pour la téléphonie.
- Dans ce cas, le signal qui circule
dans la fibre optique est de nature électromagnétique.
► Quel canal de transmission
utilise-t-on pour la télévision ?
- Le milieu de transmission est l’atmosphère terrestre.
- Les signaux sont de nature
électromagnétique (ondes hertziennes).
-
On utilise des antennes
émettrices et réceptrices, des satellites géostationnaires, des
paraboles, …
1)-
Signal analogique et signal numérique.
► Exemples de grandeurs
analogiques :
-
L’intensité sonore de la voix, la
pression atmosphérique, la température, la vitesse du vent, …
![]() Les
grandeurs analogiques varient de façon continue au cours du
temps.
Les
grandeurs analogiques varient de façon continue au cours du
temps.
-
Grâce à des capteurs
électroniques, on peut convertir ces grandeurs analogiques en
signaux électriques.
-
Exemple : le microphone convertie
l’intensité sonore de la voix en signal électrique.
-
Si le signal électrique observé
varie de façon continue au cours du temps, il est dit
analogique.
-
Si le signal électrique observé
varie par paliers, il est dit numérique.
![]() Les
grandeurs numériques varient de façon discrète au cours du
temps.
Les
grandeurs numériques varient de façon discrète au cours du
temps.
-
Exemple : La représentation d'un
signal analogique peut être représentée par
une courbe, tandis qu'un signal numérique pourra être
visualisé par un histogramme.

► Évolutions :
- Les systèmes de mesure analogique sont progressivement remplacés par des systèmes d’acquisition numérique.
- Le stockage, la duplication et le transport des signaux numériques sont plus fiables.
- Les
ordinateurs ne traitent que des signaux numériques.
![]() Les
informations numériques sont codées en langage binaire.
Les
informations numériques sont codées en langage binaire.
- Un système numérique est composé de circuits électroniques.
- Chacun d’eux peut fournir deux
niveaux de tension électrique :
-
Une tension basse codée 0
-
Et une tension haute notée 1.
-
On parle de langage binaire.
► Le bit :
- Un bit est la plus petite unité d’information numérique.
- Il ne peut prendre que deux valeurs : 0 ou 1.
3)- De
l’analogique au numérique.
a)-
Schématisation d’un convertisseur
analogique-numérique (CAN).
-
Exemple : Du « son » analogique
au « son » numérique :
b)-
La résolution du convertisseur :
-
La plus petite variation de
tension analogique que peut repérer un convertisseur est appelée
la résolution ou pas du convertisseur.
- Cette résolution dépend du nombre de bits du convertisseur et de son calibre.
- Elle
s’exprime en volt (V).
► Caractéristiques du CAN System
SPS.
|
Centrale
d’acquisition multifonctions rapide |
|
|
|
Connexion sur l’ordinateur via
le bus USB 2.0 HIGHT SPEED (480 Mbit /
s) |
|
Étage d’entrée analogique à 4 convertisseurs 12 bits, 10
Mhz |
|
Calibre d’entrées ± 10 V, ± 5
V, ±1 V et ± 0,2 V. |
-
Le calibre :
-
Il définit l’intervalle des
valeurs mesurables de la tension analogique à numériser.
-
La largeur de cet intervalle est
appelée plage de mesure.
-
Le pas ou la
résolution
:
-
Le pas
p d’un convertisseur [en volt (V)] dépend de son nombre de
bits n et de la plage de mesure :
-

-
C’est la plus petite variation de
tension analogique que peut repérer un convertisseur
analogique-numérique.
-
C’est le plus petit écart de
tension entre deux points du signal numérisé.
-
La résolution ou pas du
convertisseur fixe les valeurs que pourra prendre la tension
mesurée.
-
Ces valeurs sont des multiples
entiers du pas.
► Exemple : Calibres et résolutions
d’un convertisseur de système d’acquisition de 12 bits.
|
Calibre (V) |
Plage de mesure
(V) |
Pas p
(mV) |
|
– 10 ; + 10 |
20 |
|
|
– 5 ; + 5 |
10 |
|
|
– 1 ; + 1 |
2 |
|
|
– 0,2 ; + 0,2 |
0,4 |
|
|
0 ; + 5 |
5 |
|
c)-
La numérisation du signal :
-
Il désigne le procédé qui permet
de passer d’un signal analogique à un signal numérique.
-
Les étapes principales de toute
conversion analogique-numérique sont :
-
L’échantillonnage,
-
La
quantification,
-
Et le
codage.
►
L’échantillonnage :
-
Le convertisseur
analogique-numérique prélève des échantillons du signal
analogique à intervalles de temps
Te égaux
appelés période d’échantillonnage.
-
La fréquence d’échantillonnage
fe est le nombre de prélèvements effectués par
seconde (nombre de mesures effectuées par seconde).
-
Elle définit le nombre de valeurs
prélevées au signal analogique par seconde.
-
Elle s’exprime en Hz, MHz, …
-
C’est l’inverse de la période
d’échantillonnage :
-

- Remarque :
- La fréquence d’échantillonnage est réglable.
- Elle
ne peut pas dépasser la
valeur maximale indiquée par le constructeur.
-
Exemple :
Étage d’entrée
analogique à 4 convertisseurs 12 bits, 10 Mhz
- La fréquence d’échantillonnage doit être supérieure :
- au
double de la plus haute fréquence
contenue dans le signal d’entrée afin de pouvoir reconstituer
fidèlement le signal (Critère de Shannon).
- Ainsi pour échantillonner la musique, comme l’oreille est sensible aux fréquences sonores comprises entre 20 Hz et 20kHz,
- on peut prendre une fréquence
échantillonnage de 40 kHz.
-
On perd toutes les fréquences
supérieures à 20 kHz, mais cela n’est pas grave car l’oreille
humaine ne les entend pas.
-
Ainsi, le son de qualité CD est
échantillonné à 44 kHz.
► La quantification :
-
L’échantillonnage consiste à
prélever certaines valeurs d’une fonction continue.
-
On se retrouve avec une
succession de nombres réels avec un très grand nombre de
décimales.
-
Mais la mémoire des ordinateurs
n’est pas infinie, elle est limitée.
-
Pour limiter le nombre de
valeurs, on va faire une approximation :
-
On ne va retenir que les valeurs
selon un certain pas p de quantification.
-
La quantification consiste à
affecter une valeur numérique à chaque échantillon prélevé.
-
Chaque valeur est arrondie à la
valeur permise la plus proche par défaut.
-
Le signal est donc quantifié et
ne peut prendre que certaines valeurs discrètes.
-
C’est la
quantification.
-
Cette quantification est liée aux
limites de la perception humaine et des appareils qui
transmettent le signal.
-
Exemple :
-
Pour un signal analogique variant
entre 0,00 V et 10,0 V et codé en 3 bits, on aura 23
= 8 valeurs possibles.
-
Le pas 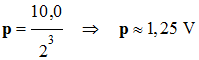
-
Les 8 valeurs de tensions
possibles :
|
Numéro |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Valeur de la tension |
0 |
1,25 |
2,50 |
3,75 |
5,0 |
6,25 |
7,50 |
8,75 |
-
Lors de la quantification, chaque
tension analogique est arrondie à la valeur la plus proche parmi
celles données.
-
Exemples :
|
Type de support |
Quantification |
Nombre de
valeurs |
|
CD Audio |
16 Bits |
216 =
65536 |
|
DVD |
24 Bits |
224 =
16777216 |
|
Téléphonie |
8 Bits |
28 =
256 |
|
Radio numérique |
8 Bits |
28 =
256 |
► Le codage :
-
La valeur permise est codée par
un nombre binaire.
-
Les valeurs numérisées vont être
stockées sous forme de bits.
-
Un bit est une unité
d’information qui ne peut prendre que deux valeurs : 0 ou 1.
-
Avec 2 bits, on 22 =
4 ; valeurs associées : 00 ; 01 ; 10 ; 11
-
Avec 3 bits, 23 = 8 ;
valeurs associées : 000 ; 001 ; 010 ; 011 ; 100 ; 101 ; 110 ;
111.
-
Ainsi de suite :
-
Un signal numérisé sur 8 bits (un
octet), peut prendre 28 = 256 valeurs.
-
De 0000 0000 à 1111 1111.
![]() La
qualité de la conversion analogique-numérique, ou numérisation,
est d’autant plus grande :
La
qualité de la conversion analogique-numérique, ou numérisation,
est d’autant plus grande :
- que le pas p du convertisseur est petit
- et que la fréquence
fe
d’échantillonnage est élevée.
d)-
Paramètres d’une numérisation.
-
La qualité d’une conversion
dépend essentiellement de la valeur de la fréquence
d’échantillonnage fe et de celle du pas
p
des mesures.
-
Le signal numérisé est d’autant
plus proche du signal analogique que :
-
La fréquence d’échantillonnage
est grande, la durée entre deux mesures est alors plus faible :
quand fe
↑, alors Te
↓.
-
Le pas
p du convertisseur
est plus faible : les mesures sont alors codées sur un nombre
plus important de valeurs binaires.
► Remarque :
-
Ces deux choix sont limités car
ils impliquent une augmentation du nombre de données à traiter.
-
Ainsi, la numérisation d’un son à
une fréquence d’échantillonnage élevée améliore sa qualité mais
limite la durée de l’enregistrement ou nécessite une plus grande
capacité de stockage.
-
Exemple 1 :
-
Signal sonore échantillonné en
qualité CD : 44 kHz, 16 bits.
-
On considère un signal stéréo (2
voies)
-
Chaque seconde : 2
× 16
× 44
× 103 bits = 1,41 Mbits
-
Valeur en octet : 1 octet = 8
bits
-
Pour une seconde de son
échantillonné à 44 kHz : 176 ko.
-
Pour un morceau de musique de 5
min : 52,8 Mo.
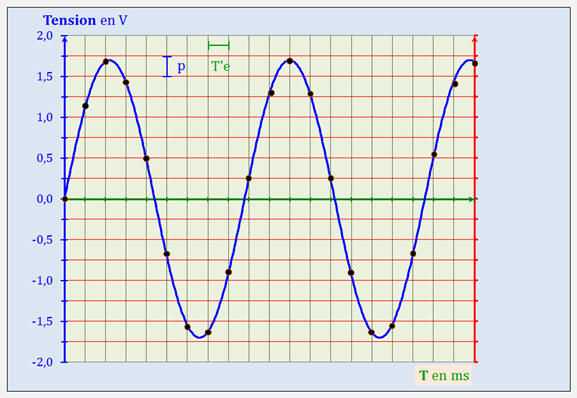
► Exemple 2 : Carte d’acquisition
de résolution 4 bits avec fréquence d’échantillonnage
fe.
-
Elle offre 24 = 16
combinaisons possibles.
-
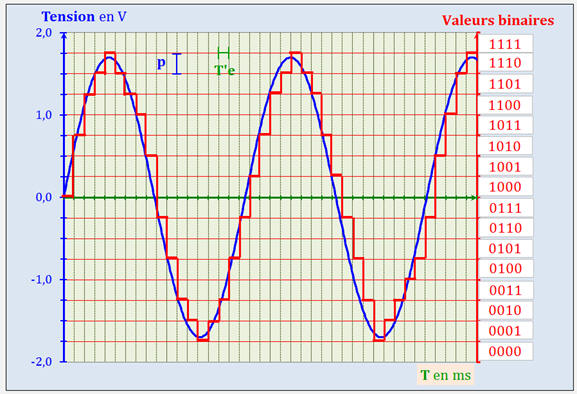
Exemple : Échantillonnage d’un
signal analogique :
-
Points de la courbe obtenue après
échantillonnage à la période Te.
-
Valeurs obtenues après
quantification du signal :
segment
rouge
-
Autre présentation :
allure du signal numérisé en rouge
Signal analogique (en bleu)
et signal numérisé (en rouge) par une carte d’acquisition 4
bits.
-
Les valeurs mesurées sont
traduites par un code de 4 bits, offrant 16 combinaisons
possibles.
-
Aux valeurs
comprises entre
– 2 V et – 1,75 V, on associe la combinaison 0000,
-
Aux valeurs
comprises + 1,75 V et 2 V, on associe la combinaison
1111.
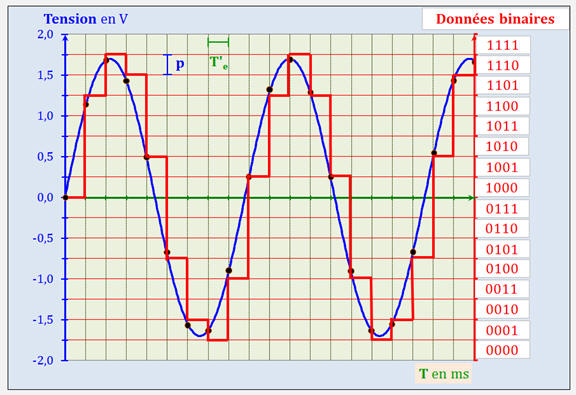
|
Plage de valeurs de la
tension (V) |
–2,00
< u ≤ – 1,75 |
– 1,75 < u ≤ – 1,50 |
– 1,50 < u ≤ – 1,25 |
– 1,25 < u ≤ – 1,00 |
– 1,00 < u ≤
– 0,75 |
– 0,75 < u ≤
– 0,50 |
– 0,50 < u ≤
– 0,25 |
– 0,25 < u ≤
0,00 |
|
Valeurs
binaires |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
|
Plage de valeurs de la
tension (V) |
0,00
< u ≤ 0,25 |
0,25
< u ≤ 0,50 |
0,50
< u ≤ 0,75 |
0,75
< u ≤ 1,00 |
1,00 < u ≤ 1,25 |
1,25 < u ≤
1,50 |
1,50 < u ≤ 1,75 |
1,75 < u ≤
2,00 |
|
Valeurs
binaires |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
-
Valeur du pas : 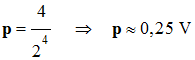
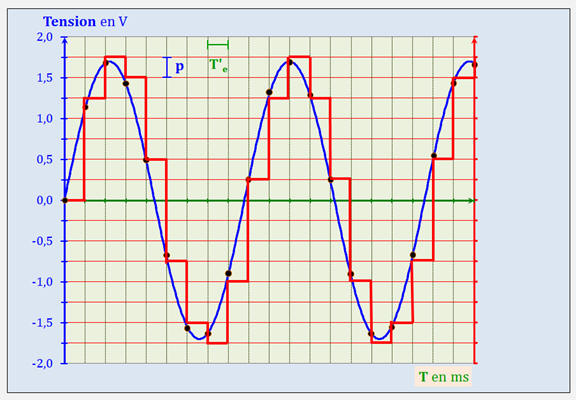
► Exemple : Carte d’acquisition de
résolution 4 bits avec fréquence d’échantillonnage
f’e = 2
fe.
-
On a toujours 16 combinaisons
possibles, mais 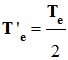
Signal analogique (en bleu)
et signal numérisé (en rouge) par une carte d’acquisition 4
bits.
-
Les valeurs mesurées sont
traduites par un code de 4 bits, offrant 16 combinaisons
possibles.
-
Aux valeurs
comprises entre
– 2 V et – 1,75 V, on associe la combinaison 0000,
-
Aux valeurs
comprises + 1,75 V et 2 V, on associe la combinaison
1111.
|
Plage de valeurs de la
tension (V) |
–2,00
< u ≤ – 1,75 |
– 1,75 < u ≤ – 1,50 |
– 1,50 < u ≤ – 1,25 |
– 1,25 < u ≤ – 1,00 |
– 1,00 < u ≤
– 0,75 |
– 0,75 < u ≤
– 0,50 |
– 0,50 < u ≤
– 0,25 |
– 0,25 < u ≤
0,00 |
|
Valeurs
binaires |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
|
Plage de valeurs de la
tension (V) |
0,00
< u ≤ 0,25 |
0,25
< u ≤ 0,50 |
0,50
< u ≤ 0,75 |
0,75
< u ≤ 1,00 |
1,00 < u ≤ 1,25 |
1,25 < u ≤
1,50 |
1,50 < u ≤ 1,75 |
1,75 < u ≤
2,00 |
|
Valeurs
binaires |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
-
Le pas
p ne change pas.
-
Comme dans ce cas :
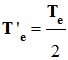 , davantage
d’échantillons sont mesurés sur la même durée.
, davantage
d’échantillons sont mesurés sur la même durée.
-
L’allure de la courbe rouge se
rapproche davantage de l’allure de la courbe bleue du signal
analogique.
III- Caractéristiques d’une image numérique.
1)-
Introduction. (Rappels de Première S)
-
Une image numérique peut être
affichée sur un écran plat, une tablette ou un téléphone
androïde.
-
Les écrans qui équipent les
téléviseurs, les téléphones portables, les écrans d’ordinateurs
utilisent le principe de la trichromie et de la synthèse
additive.
-
L’écran plat d’un téléviseur est
divisé en petites unités lumineuses : les pixels.
-
Chaque pixel est constitué de
trois sous-pixels : trois luminophores
-
Un luminophore qui diffuse de la
lumière rouge
-
Un
luminophore qui diffuse de la lumière verte
-
Un luminophore qui diffuse de la
lumière bleue
-
En agissant sur le réglage de
l’intensité lumineuse de chaque luminophore, on arrive à obtenir
la couleur voulue pour chaque pixel.
-
Un écran est caractérisé par sa
définition, c’est-à-dire par le nombre total de pixels.
-
Les fabricants indiquent :
-
Le nombre de pixels par ligne et
le nombre de lignes.
-
Un écran, haute définition HD,
possède :
-
1080 lignes de 1920 pixels
chacune et la taille d’un pixel est liée à la taille de l’écran.
-
Plus l’écran est petit, plus le
pixel est petit.
- Une image est constituée de points ou pixels.
- On parle de pixellisation de l’image.
-
Si elle est regardée à une
distance suffisante, l’œil ne peut distinguer la trame des
pixels.
-
L’œil possède un pouvoir
séparateur.
- Si l’écart entre 2 pixels est inférieur à une minute d’angle, l’œil ne peut pas séparer les deux points.
- L’image paraît ainsi uniforme.
-
Vue agrandie d’une partie de
l’écran d’un téléviseur.
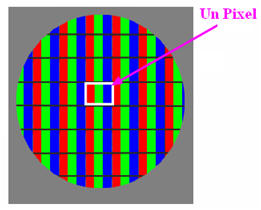
-
Couleurs des différents
luminophores et couleur observée à l’écran :






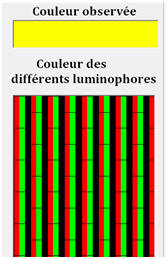
Mire d’un écran de
télévision

2)- Le
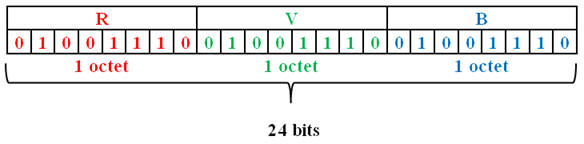
codage des pixels en couleur.
-
Parmi les différents codages, le
codage RVB
24 bits est le plus utilisé.
-
Chaque sous-pixel ou luminophore
est codé sur un octet, constitué par une séquence de huit bits.
-
Un bit ne pouvant prendre que
deux valeurs (0 ou 1),
-
La plus petite valeur possible
d’un octet est :
-
00000000
-
La plus grande valeur possible
est :
-
11111111
-
En numération décimale, un octet
peut prendre toutes les valeurs entières possibles entre 0 et
255.
-
Une image numérique est
généralement codée en
RVB
24 bits.
-
Le codage
RVB
permet d’associer trois nombres à une couleur.
-
Les 24 bits correspondent à 3
x 8 bits, c’est-à-dire à 3 octets.
-
Pour coder les couleurs d’un
pixel, 8 bits sont alors consacrés au rouge, 8 bits au vert et
enfin 8 bits au bleu.
-
Chaque sous-pixel peut prendre 28
=256 nuances.
-
Ainsi le sous-pixel rouge peut
émettre 256 nuances de rouge.
-
Le sous-pixel vert peut émettre
256 nuances de vert.
-
Le sous-pixel bleu peut émettre
256 nuances de bleu.
-
Le mélange de ces trois
sous-pixels peut recréer :
-
256
x 256
x 256 = 16 777 216 lumières colorées différentes.
-
Soit plus de 16 millions de
couleurs.
► Remarque :
-
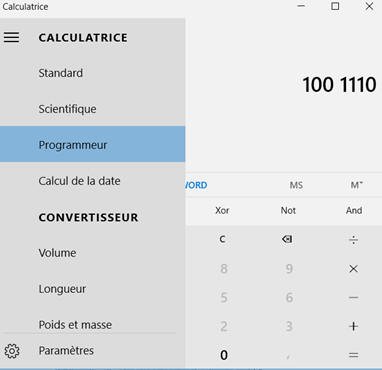
Pour réduire la longueur de
l’écriture des codages, on utilise aussi l’écriture hexadécimale
(en base 16).
-
On peut passer d’une écriture à
l’autre à l’aide de certains tableurs, calculatrices ou
application en ligne.
-
Calculatrice Microsoft : en mode
PROGRAMMEUR : Convertisseur Microsoft.
-
Tableau de correspondance
Décimal, Binaire et Hexadécimal :
|
Décimal |
Binaire |
Hexadécimal |
|
0 |
00000000 |
0 |
|
1 |
00000001 |
1 |
|
2 |
00000010 |
2 |
|
3 |
00000011 |
3 |
|
4 |
00000100 |
4 |
|
5 |
0000101 |
5 |
|
6 |
0000110 |
6 |
|
7 |
0000111 |
7 |
|
8 |
0001000 |
8 |
|
9 |
0001001 |
9 |
|
10 |
0001010 |
A |
|
11 |
0001011 |
B |
|
12 |
0001100 |
C |
|
13 |
0001101 |
D |
|
14 |
0001110 |
E |
|
15 |
0001111 |
F |
|
16 |
0010000 |
10 |
|
|
|
|
|
255 |
11111111 |
FF |
3)-
Application :
Chap. N° 02 Couleurs
des objets (première S)
a)-
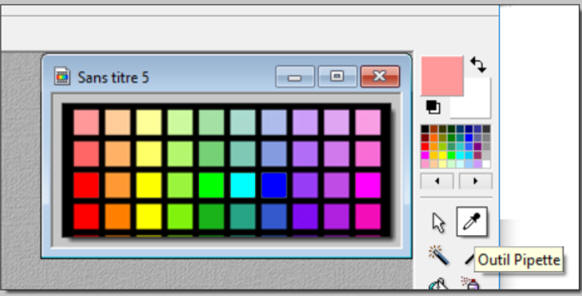
Utilisation du Logiciel
PHOTOFILTRE et d’une mire.
-
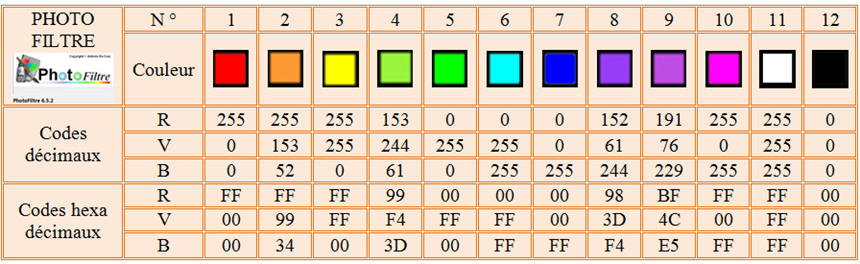
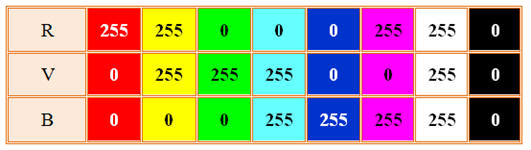
On va utiliser la mire ci-dessous
que l’on va analyser avec le logiciel
PHOTOFILTRE.

-
On place la pipette dans les
différentes zones colorées et on relève les codes décimaux
et hexadécimaux associés à une dizaine de couleurs.
-
On prendra la ligne suivante à laquelle on ajoutera le
blanc et le noir:
![]()
-
Donner les résultats sous forme
d’un tableau :
-
Mise en évidence de la synthèse
additive des couleurs en analysant les différentes valeurs du
tableau :
-
Exemple :
-
Le code hexadécimal suivant,
FF0000, correspond en regroupant les valeurs deux à deux :
-
Les deux premières valeurs FF
sont liées au
rouge,
-
Les deux valeurs suivantes 00
sont liées au
vert
-
Et les deux dernières valeurs 00
sont liées au
bleu.
-
FF-00-00
pour le codage
RVB,
ce qui donne en
codage décimal :
255-0-0.
- Le code hexadécimal FF0000 désigne la couleur rouge.
- De même le code décimal (255,0,0)
désigne la couleur rouge.
► Les couleurs caractéristiques :
-
La couleur N° 1 est le rouge, N°
5, le vert et la N° 7 le bleu.
-
La couleur N° 3 est le jaune
(rouge + vert)
-
La couleur N° 6 est du cyan (vert
+ bleu)
-
La couleur
N° 10 est du magenta (rouge + bleu)
-
La couleur N° 11 est le blanc
(rouge + vert + bleu)
-
La couleur N° 12 est le noir.
Pour obtenir le noir, les trois sous-pixels doivent être
éteints.
b)-
Codage des niveaux de gris :
-
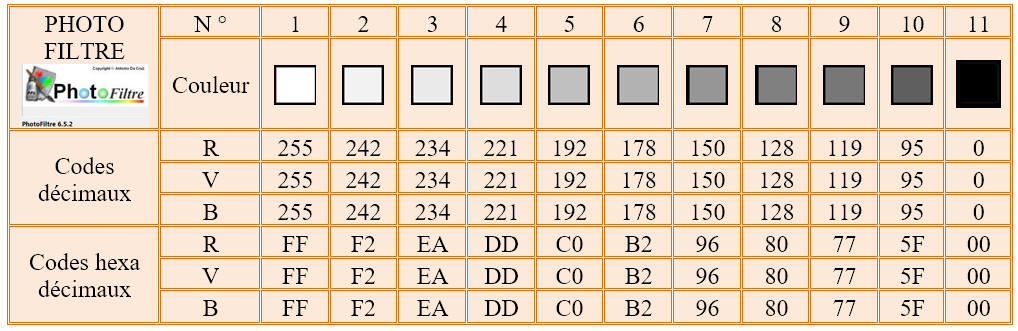
Placer la pipette dans les
différents niveaux de gris et indiquer les codes décimaux
associés aux différentes nuances de gris.
![]()
-
Présenter les résultats sous
forme de tableau :
-
On en déduit qu’un niveau de gris
est codé en
RVB
par trois fois le même nombre en codage décimal.
-
En conséquence, en nuance de
gris, un pixel est codé par 1 octet.
- La valeur de ce nombre diminue au fur et à mesure que le gris devient plus foncé.
- Il prend la
valeur zéro pour le noir.
-
Plus le gris est sombre et plus
la valeur commune aux trois sous-pixels est faible.
-
Une image numérique est composée
de pixels, eux-mêmes divisés en trois sous-pixels.
-
En codage
RVB
24 bits ou 3 octets,
chaque sous-pixels peut prendre 256 nuances.
-
On a pour un pixel : 256
x 256
x 256 couleurs, soit environ 16 millions.
-
Une image numérique est codée par
un tableau de nombre.
-
Chaque pixel de l’image numérique
est codé par 3 nombres.
-
En codage RVB 24 bits, il est
possible de réaliser 256 nuances de gris en affectant la même
valeur à chaque sous-pixel :
-
En partant du noir
R(0)V(0)B(0)
au blanc R(255)V(255)B(255)
4)-
Définition et taille d’une image numérique.
a)-
La définition d’une image
numérique :
-
La définition d’une image
numérique correspond au nombre de pixels qui constituent cette
image.
► Exemple :
-
Si une image est constituée de
640 colonnes et de 480 lignes, sa définition est égale à :
-
640
x 480 = 307 200 pixels.

b)-
Taille d’une image numérique :
-
La taille d’une image numérique
est la place qu’occupe le codage de tous les pixels qui
constituent cette image.
-
La taille s’exprime en octet.
-
Elle est donnée par la relation :
-
taille = (nombre
d’octets par pixel)
x (définition)
► Exemple :
L’image précédente
est constituée de 640 colonnes et de 480 lignes et est codée en 24 bits
(3 octets) :
-
Valeur de la taille :
-
3
x 640
x 480 = 921 600 octets.
► Remarque :
-
En réalité, la taille du fichier
correspondant est légèrement supérieure, car quelques octets
supplémentaires sont utilisés pour coder ses caractéristiques
(format, nombre de lignes, de colonnes, nom du fichier, date de
création, date de modification, …)
c)-
Préfixes décimaux et préfixes
utilisés en informatique.
-
C'est le
BIPM (Bureau International des Poids et
Mesures) qui est la référence mondiale pour les unités, et en
particulier les facteurs (kilo, Méga, Téra,...).
-
La notation kilo (k minuscule) est officiellement : 1000 = 103.
-
Cette définition est indépendante de l'unité à laquelle elle
s'accole: que ce soient des kilogrammes (kg), des kilomètres
(km), des kilojoules (kJ), des kiloampères (kA), des kilohertz
(kHz) ou des kilo-octets (ko), la définition du "kilo" ne varie
pas: c'est 103.
-
Cette mauvaise habitude du kilo-octet à 1024 est malheureusement
très fortement ancrée en informatique et elle est la source de
nombreuses erreurs d'interprétation.
-
En informatique, les capacités
mémoires sont en général des multiples de puissances de 2.
-
Pour cette raison, les
informaticiens de la première heure avaient l'habitude
d'utiliser les préfixes
kilo,
méga, etc.
... comme des puissances
de 210, soit
1 024.
-
Toutefois la Commission
électrotechnique internationale préconise, depuis 1998, l'usage
de préfixes binaires, afin d'éviter tout malentendu, même entre
informaticiens.
-
Il est préférable d'utiliser ces
préfixes :
-
kibi : 1 Ki
= 210 = 1024,
-
mébi : 1 Mi
= (210)2 = 10242 ≈ 1,049
× 106,
-
gibi : 1 Gi = (210)3 = 10243≈
1,074
× 109,
-
etc…),
-
Et de laisser aux préfixes
SI
leur sens recommandé (kilo : 1 k = 1000,
méga : 1 M = 10002,
giga : 1 G = 10003, etc…).
- Les fabricants et vendeurs de supports informatiques ne s'y sont pas trompés :
- ils préfèrent
l'usage des préfixes SI, ce qui leur permet d'afficher
des capacités apparemment plus importantes.
-
Ainsi un disque dur d'une
capacité de 1 téraoctet = 1 To = 1000 Go
correspond, avec les préfixes binaires, à une capacité de
931 gibioctets, ce qui est moins
impressionnant pour le profane.
u
Tableau :
|
Nom |
Symbole |
Facteur
Valeur |
|
Nom |
Symbole |
Facteur |
|
kibi |
Ki |
210
= 1,02
×
103 |
kilo |
k |
103 = 1 000 |
|
|
mébi |
Mi |
220 = 1,05
×
106 |
méga |
M |
106 = 1 000 000 |
|
|
gibi |
Gi |
230 = 1,07
×
109 |
giga |
G |
109 = 1 000 000 000 |
|
|
tébi |
Ti |
240 = 1,10
×
1012 |
téra |
T |
1012 = 1 000 000 000 000 |
|
|
pébi |
Pi |
250 = 1,13
×
1015 |
péta |
P |
1015 = 1 000 000 000 000 000 |
|
|
exbi |
Ei |
260 = 1,15
×
1018 |
exa |
E |
1018 = 1 000 000 000 000 000 000 |
|
|
zébi |
Zi |
270 = 1,18
×
1021 |
zetta |
Z |
1021 = 1 000 000 000 000 000 000 000 |
|
|
yobi |
Yi |
280 = 1,21
×
1024 |
yotta |
Y |
1024 = 1 000 000 000 000 000 000 000 000 |
-
En conséquence, il ne faut pas
confondre 1 ko = 1000 octets et Kio = 1024 octets.
► L’image suivante
est constituée de
640 colonnes et de 480 lignes et est codée en 24 bits (3 octets) :
![]() Donner
la taille de l’image suivante
en Kio :
Donner
la taille de l’image suivante
en Kio :
-
Image 640
x 480 codé en 24 bits (8 octets) :

-
Définition de l’image :
-
640
× 480 = 307 200
-
Taille de l’image en ko :
-
taille = (nombre
d’octets par pixel)
x (définition)
-
taille =
(3)
× (640
× 480) = 921 600 octets.
-
taille =
3
x 307 200 = 921 600 octets.
-
Taille de l’image en Kio :
-
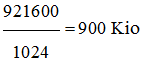
► L’image
suivante est constituée de 50 colonnes et de 50 lignes et
est codée en 24 bits (3 octets) :

-
La définition de cette image est
de :
-
50
× 50 = 2500 pixels.
-
Si on agrandie (1200 fois) cette
image, on voit apparaître les pixels :

-
La taille de cette image en 24
bits (3 octets) est :
-
3
× 50
× 50 = 7500 octets ≈ 7,32 kibioctets = 7,32 Kio
► L’image suivante est constituée de 640 colonnes et
de 480 lignes et est codée en 24 bits (3 octets) :

-
Cette image a une définition de :
-
500
x× 500 = 250000 pixels
-
La taille de cette image en 24
bits (3 octets) est :
-
3
× 500
× 500 = 750000 octets ≈ 732,4 kibioctets = 732,4 Kio
1)- La
numérisation d’un signal : exercice 21 page 532.
|
Le signal électrique
correspondant à un son musical affiché sur l’écran
d’un oscilloscope analogique est reproduit
ci-dessous.
Sensibilité
verticale : 1,0 V / div Sensibilité
horizontale : 2,0 ms / div.
Donnée :
pas :
1)-
La fréquence d’échantillonnage étant de 1,0 kHz,
quelle est la durée séparant deux mesures
consécutives ? 2)-
Le CAN : a)-
Le CAN étant de 6
bits avec une plage de mesure de 0,00 V à 10,0 V,
calculer le pas du convertisseur. b)-
Indiquer les huit
premières valeurs que peut quantifier le
convertisseur à partir de 0,00 V. 3)-
La date t = 0 correspond au bord gauche de
l’écran de l’oscilloscope. Reproduire et compléter
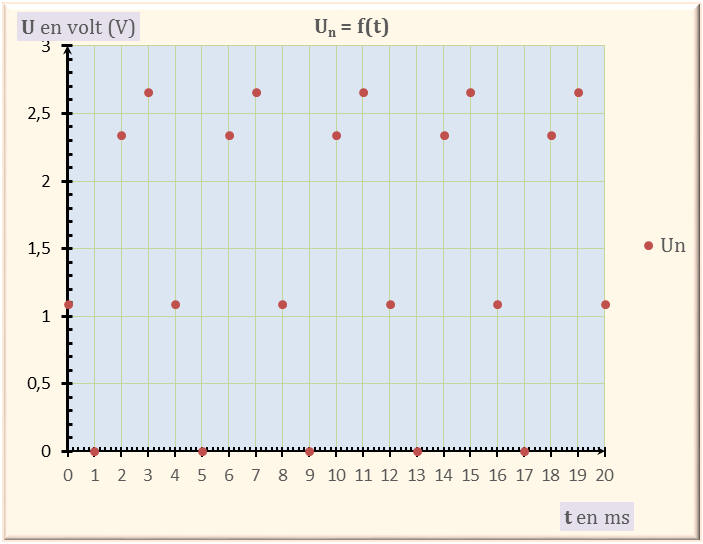
le tableau suivant : -
On donne :
Sensibilité verticale : 1,0 V / div -
Sensibilité
horizontale : 2,0 ms / div.
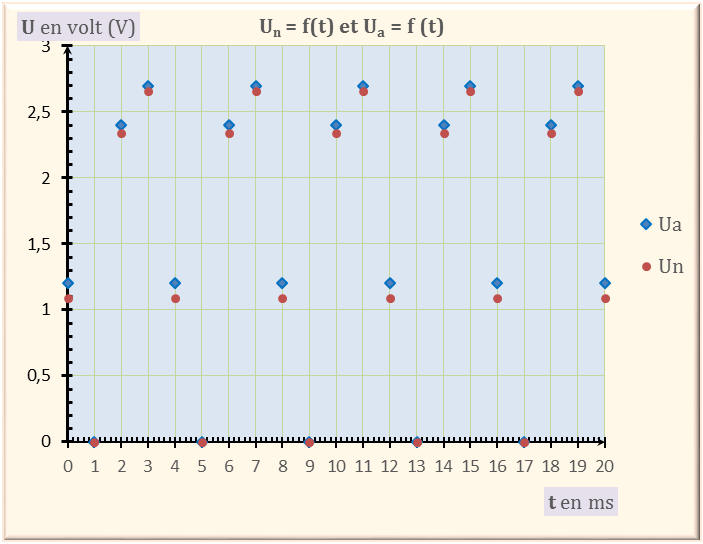
4)-
En utilisant les échelles de représentation
suivantes : -
1 cm
→ 2 ms et 1 mm
→ pas de résolution -
Représenter le signal
numérique. |
|
1)-
Durée séparant deux mesures consécutives : -
La fréquence
d’échantillonnage est f = 1,0 kHz -
On en déduit la
période T d’échantillonnage : -
2)-
Le CAN : a)-
Pas du
convertisseur : -
Le CAN étant de 6
bits avec une plage de mesure de 0,00 V à 10,0 V, - Pour un signal analogique variant entre 0,00 V et 10,0 V et codé en 6 bits : - on aura 26 = 64 valeurs
possibles. -
Le pas du
convertisseur est donné par la relation suivante : -
b)-
Les huit premières
valeurs que peut quantifier le convertisseur à
partir de 0,00 V.
3)-
Tableau de valeurs : -
On visualise les
différents points retenus du signal analogique en
jaune. -
Points de la courbe obtenue après
échantillonnage à la période T.
4)-
Signal numérique : -
Les échelles : -
En abscisse :1 cm
→ 2 ms -
En ordonnée : 1 mm
→ pas de résolution -
Représentation
graphique du signal numérique : -
Tableau de valeurs :
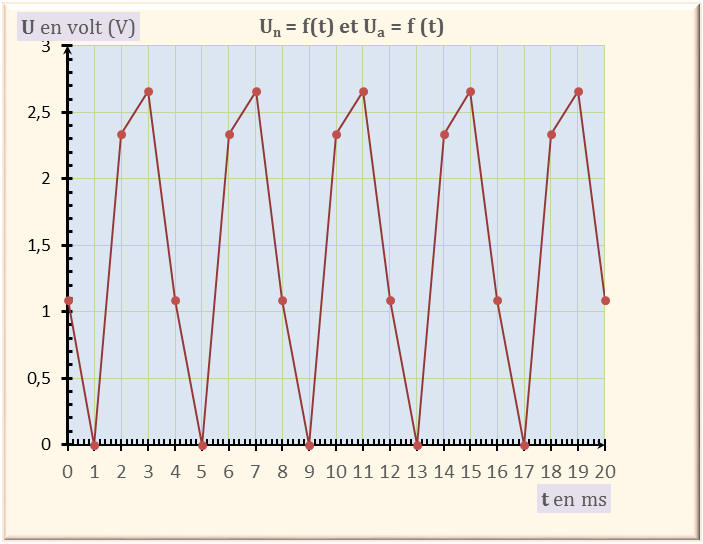
- Le signal analogique a été quantifié. - Le signal numérique ne peut prendre
que certaines valeurs discrètes. -
Autre
représentation : allure du signal numérique Graphe N° 3
|
|
QCM réalisé avec le
logiciel Questy |
3)-
Exercices :
a)-
Exercice 8 page 529 : Définir un
signal numérique.
b)-
Exercice 9 page 530 : Calculer
une fréquence d’échantillonnage.
c)-
Exercice N° 13 page 530 :
Associer un tableau de nombres à une image numérique.
d)-
Exercice 15 page 531 :
échantillonnage et CD.
e)-
Exercice 16 page 531 :
Acquisition d’une carte d’acquisition.
f)-
Exercice 20 page 532 : Le réseau
téléphonique.
g)-
Exercice 24 pages 533 et 534 :
Critère de Shannon et théorie de l’échantillonnage.
h)-
Exercice 30 page 537 : Appareil
photo numérique.
|
|