-  Schéma :

-  Expression vectorielle :

3)- La force électrostatique.

-  Dans le vide, deux particules A et B, portant les charges électriques respectives q_A et q_B, séparées par la distance r sont soumises à deux forces directement opposées :

-  

-  Expression :

-  Premier cas : on considère que :   q_A . q_B > 0

-  Deuxième cas : on considère que :   q_A . q_B < 0

-  Étude de l’expression :

-    : vecteur unitaire : direction droite (AB) et sens de A vers B.

-  k : constante

-  r : distance séparant les deux charges électriques en mètre m.

-  F : force électrique en Newton N.

-  Application : la molécule de dichlore.

-  Force d’interaction électrique entre les noyaux :

- 

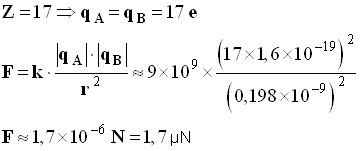
-  échelle : 1 cm ↔ 1 N 

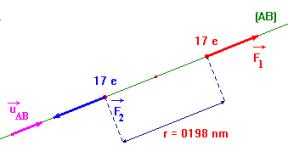
4)- Analogies et différences avec les forces de gravitation.

-  Analogies : les forces électriques et les forces de gravitation, sont :

-  Proportionnelles aux grandeurs qui les créent

-  Et inversement proportionnelle au carré de la distance.

-  Différences :

-  Les forces de gravitation sont toujours attractives alors que les forces électriques sont attractives ou répulsives.

-  À l’échelle macroscopique les forces électriques sont négligeables devant les forces de gravitation,

-  À l’échelle microscopique les forces de gravitation sont négligeables par rapport aux forces électriques.

-  Attention : Pour la valeur de la force : les charges sont des grandeurs algébriques.

-  Pour ne pas avoir de problème :

-  il faut écrire :  et pour l’expression vectorielle : .

5)- Mouvement d’un corps soumis à ce type de forces.

a)-     Exemple 1.

-  Considérons un corps T de masse respectives m_T et un corps S de masse  m_S avec : m_T >>  m_S.

-  On étudie le mouvement de S par rapport à T dans le référentiel galiléen lié à T.

-  Dans cet exemple T peut représenter la Terre et S un satellite de la Terre.

-  cette force est orientée vers le centre de la Terre, c’est une force centripète.

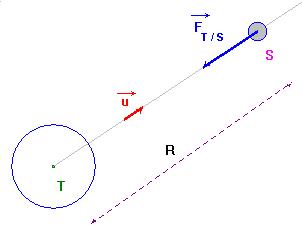
-  Le mouvement du corps S est soit circulaire, elliptique ou hyperbolique. 

-  Cela dépend de la vitesse du satellite dans le référentiel d’étude.

b)- Exemple 2.

-  Considérons un proton P (charge e) et un électron E (charge – e).

-  On étudie le mouvement de E par rapport à P dans un référentiel galiléen lié à P.

-  Cet exemple peut représenter un atome d’hydrogène.

-  L’électron E est soumis à une force électrostatique attractive. 

-  Cette force est orientée vers le centre du proton P, c’est une force centripète.

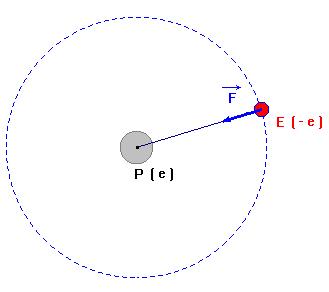
-  Le mouvement de E  est soit circulaire, elliptique ou hyperbolique.

-  Cela dépend de la vitesse de E dans le référentiel d’étude.

c)- Conclusions.

-  Les deux types de forces conduisent aux mêmes types de mouvements du centre d’inertie des objets.

-  C’est à partir de cette constatation que le modèle planétaire de l’atome d’hydrogène a été élaboré (RUTHERFORD).

-  Dans les deux cas, il y a une infinité de trajectoires passant par un point quelconque donné.

-  Le mouvement est complètement déterminé si on connaît les conditions initiales. 

-  Il y a autant de trajectoires que de conditions initiales.

II- Les limites de la mécanique de Newton.

1)- Énergie du système S = {planète + satellite}.

-  Un satellite de la Terre évolue sur une orbite bien déterminée.

-  Dans le référentiel géocentrique, il possède une vitesse v et une altitude h.

-  Le système S possède une énergie E.

-  Toutes les altitudes et toutes les vitesses sont possibles.

-  L’énergie d’un tel système peut prendre n’importe quelle valeur.

-  L’énergie d’un tel système peut varier continûment.

2)- Énergie du système S = {proton + électron} de l’atome d’hydrogène.

-  À  partir du modèle planétaire de l’atome d’hydrogène, on peut prévoir pour ce système toutes les énergies possibles.

- Ce modèle est-il en accord avec la réalité ?

-  Comment peut-on interpréter le spectre de la lampe à hydrogène ?

-  Pour obtenir ce spectre, on soumet de l’hydrogène à des décharges électriques dans une ampoule

-  Ce dispositif fournit de l’énergie aux atomes d’hydrogène.

-  Les atomes gagnent de l’énergie et se retrouvent dans un état excité instable.

-  Ils se désexcitent spontanément pour retrouver un état plus stable et une énergie plus basse.

-  Au cours de cette désexcitation, ils émettent de l’énergie lumineuse.

-  On observe un spectre de raies et non un spectre continu.

-  Les fréquences des radiations émises ne peuvent prendre que certaines valeurs particulières.

-  On dit que les fréquences sont quantifiées.

-  Ce spectre de raies est caractéristique de l’hydrogène, il permet de l’identifier.

-  Un atome d’hydrogène ne peut prendre que certains niveaux d’énergie.

-  Ceci est en contradictions avec la mécanique de Newton.

3)- Le photon et les hypothèses de BOHR.

-  En 1900, Max Planck fut conduit à postuler la quantification de l’énergie transportée par les ondes électromagnétiques.

-  Il postule que l’énergie électromagnétique ne peut s’échanger que par « paquets » ou quanta d’énergie.

-  En 1905, Albert Einstein émet l’idée que ces quanta d’énergie sont transportés par des photons.

-  Les photons sont des particules de masse nulle et de charge nulle se propageant à la vitesse de la lumière.

-  Énergie d’un photon :  E = h . υ

-  Pour une onde électromagnétique de fréquence υ et de longueur d’onde λ dans le vide

-  La grandeur h est la constante de Planck : h = 6,62 x 10 ^{– 34}  J.s.

-  En 1913, BOHR énonce les postulats suivants :

►  Les variations d’énergie d’un atome sont quantifiées.

►  L’atome ne peut exister que dans certains états d’énergie ou niveaux d’énergie bien définis.

►  Un photon de fréquence υ est émis lorsque l’atome effectue une transition d’un niveau d’énergie E_p vers un niveau inférieur E_n tel que : 

►  E_p – E_n = h . υ

►  Il résulte de ceci que les énergies d’un atome sont quantifiées. 

►  Contrairement à l’énergie du système S = {planète + satellite}, l’énergie du système  {proton + électron} ne peut prendre que certaines valeurs discrètes. 

►  Le modèle planétaire de l’atome est à rejeter.

4)- Conclusions.

-  Ce qui est vrai pour l’atome d’hydrogène est vrai aussi  pour les autres atomes. 

-  Ceci reste valable pour les molécules qui sont des associations d’atomes.

-  Il en va de même pour les noyaux des atomes. 

-  C’est pour cette raison que lors de la désexcitation d’un noyau, il y a émission d’un rayonnement γ.

-  L’énergie d‘un atome est quantifiée, l’énergie d’une molécule est quantifiée et l’énergie d’un noyau est quantifiée.

III- Niveaux d’énergie électroniques d’un atome.

1)- Définition des niveaux d’énergie.

-  Les échanges d’énergie liés aux transitions atomiques sont de l’ordre de l’électronvolt.

1 eV = 1,6 x 10^–19  J

2)- application : 

Solution : -  Rapport des valeurs des forces gravitationnelle et électrique : -  Application numérique :   -   -  L’interaction gravitationnelle est très négligeable devant l’interaction électrostatique. -  Ce résultat est indépendant de la distance entre le proton et l’électron. -  Valeur de l’énergie de l‘atome d’hydrogène dans l’état fondamental. -  Dans l’état fondamental, n = 1 : E1 = – 13,6 eV. -  Diagramme d’énergie des cinq premiers niveaux d’énergie. n 1 2 3 4 5 En    en eV – 13,6 – 3,40 – 1,51 – 0,85 – 0,54   -  Valeur du nombre n. -  L’énergie absorbée par l’électron est donnée par la relation : -  L’énergie absorbée par l’électron est donnée par la relation : -  -  Ce qui  correspond sensiblement à la transition entre les niveaux 1 et 3 : -  n = 3. -  Longueur d’onde des différents photons. -  L’atome peut se désexciter directement vers son état fondamental. -  L’atome peut se désexciter en passant par le niveau intermédiaire : -  Longueur d’onde associée à la transition n = 3 à n = 1. -   -  Application numérique : -  Seule la radiation rouge λ32 ≈ 657 nm est dans le domaine du visible, les deux autres sont dans U.V.

-  Spectre de l'atome d'hydrogène : voir  Exercice 38 page 379

IV- Niveaux d’énergie des molécules et des noyaux.

1)- Les molécules.

-  Les molécules sont le plus souvent constituées de plusieurs atomes.

-  Dans le calcul de l’énergie d’une molécule il faut tenir compte de l’énergie de vibration, mais aussi de l’énergie de rotation.

-  Les vibrations d’une molécules sont dues aux oscillations des atomes autour d’une position d’équilibre.

-  Une molécule peut aussi posséder des mouvements de rotation autour de différents axes.

-  Cela dépend de la géométrie de la molécule.

-  Les molécules présentent des niveaux d’énergie quantifiés.

-  Chaque niveau est associé à un état de vibration et de rotation donné.

-  Les spectres moléculaires sont plus complexes que les spectres atomiques.

-  Le spectre de raies d’absorption typique d’une molécule montre des séries de raies très proches les unes des autres.

-  L’énergie correspondante à ces transitions est de l’ordre du meV.

-  Avec les spectroscopes usuels dont le pouvoir de résolution est faible, les raies sont très proches les unes des autres, on observe des bandes noires d’absorption.

2)- Les noyaux.

-  L’énergie des noyaux est également quantifiée.

-  Un noyau peut effectuer des transitions de niveau d’énergie par émission ou absorption d’un photon.

-  Un noyau peut aussi être excité par la collision avec une particule suffisamment énergétique.

-  Les transitions nucléaires sont très énergétiques. Les énergies échangées lors des transitions sont de l’ordre du MeV.

-  Les photons émis ou absorbés sont du domaine des rayons γ.

-  Exemple : Une désintégration radioactive s’accompagne le plus souvent de l’émission de photons γ.

-  Souvent, après la désintégration, le noyau-fils se retrouve dans un état excité.

-  Il se désexcite alors pour revenir dans son état fondamental par émission d’un ou plusieurs photons γ.

V- Applications. 

1)- QCM :

2)- Exercices :