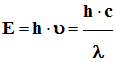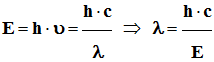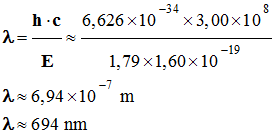I- Ondes ou particules.

1)- La lumière.

a)-   Introduction,

-   Les phénomènes de diffraction et d’interférences de la lumière s’expliquent par ses propriétés ondulatoires.

-   (Chap. N° 03 Propriétés des Ondes.) Modèle ondulatoire de la lumière 2004

-   En 1900, Max Planck fut conduit à postuler la quantification de l’énergie transportée par les ondes électromagnétiques.

-   Il postule que l’énergie électromagnétique ne peut s’échanger que par « paquets » ou quanta d’énergie.

-   En 1905, Albert Einstein émet l’idée que ces quanta d’énergie sont transportés par des photons.

-   Les photons sont des particules de masse nulle et de charge nulle se propageant à la vitesse de la lumière.

b)-  Énergie d’un photon.

-   L’énergie de la lumière est transportée par des photons qui présentent un aspect particulaire et un aspect ondulatoire.

-   L’énergie d’un photon est donnée par la relation :

-   E = h . υ

-   L’énergie E représente l’aspect particulaire du photon.

-   La fréquence υ représente son aspect ondulatoire.

-   Pour une onde électromagnétique de fréquence υ et de longueur d’onde λ dans le vide,

-   On peut écrire :

2)- La matière.

-   À toute particule matérielle de masse m animée d’une vitesse de valeur v très petite devant la célérité de la lumière, on associe une grandeur physique appelée quantité de mouvement.

-   La valeur de la quantité de mouvement, notée p est définie par la relation suivante :

 

 

-   En 1923, le physicien français Louis de Broglie propose que la dualité onde-particule s’applique aussi à toute particule matérielle.

-   La dualité onde-corpuscule conduit à associer une onde de longueur d’onde λ à toute particule, matérielle ou non, de quantité de mouvement p telle que :

 

-    En conséquence :

-   L’aspect ondulatoire se manifeste d’autant plus que la masse de la particule est petite.

-   C’est le cas pour les particules microscopiques comme l’électron, le proton et le neutron.

-   Lorsque la masse de la particule est grande, la longueur d’onde associée est tellement faible que l’on ne peut pas mettre en évidence les phénomènes de diffraction et d’interférence.

-   Il n’existe aucune ouverture suffisamment petite pour pouvoir diffracter l’onde associée à la particule.

-   Les unités : montrer que (kg . m . s ^{– 1}) = (J.s) . (m^{– 1}).

-   (J) = (N . m) = (kg . m . s^–2. m) = (kg . m² . s^–2)

-   (J.s) . (m^{– 1}) = ((kg . m² . s^–2). s) . (m^{– 1}) = (kg . m . s^–1)

3)- Interférences particule par particule.

-   Fentes d’Young.

 

-   On éclaire des fentes d’Young avec une source lumineuse (Laser).

-   Un écran placé derrière les fentes repère l’impact des photons.

-   On observe une figure d’interférence.

-   On diminue l’intensité de la lumière de telle sorte que les photons arrivent par un sur les fentes.

-   En raison de cette discontinuité, on parle de phénomène quantique.

-   Dans ces conditions, on ne peut pas prévoir le lieu de l’impact des photons sur l’écran.

-   Par contre, on peut établir une probabilité de les observer à un endroit précis.

-   Pour un grand nombre d’impacts, cette probabilité est maximale à certains endroits et minimale à d’autres.

-   Avec cette expérience, on a mis en évidence l’aspect probabiliste du phénomène.

 Les phénomènes quantiques présentent un aspect probabiliste :

On peut au mieux établir la probabilité de présence de la particule à un endroit donné.

II-  Fonctionnement d’un laser.

1)- Introduction.

-   Le terme laser est l’acronyme de LIGHT AMPLIFICATION BY STIMULED EMISSION OF RADIATION signifiant « amplification lumineuse par émission stimulée de rayonnement ».

2)- Émission spontanée de photons.

-   Cours de première : Chap. N° 03 Sources de lumières colorées. (Quantification de l’énergie des atomes).

-   Un atome, un ion ou une molécule excités peuvent libérer leur énergie par émission spontanée d’un photon.

-   Exemple de l’atome :

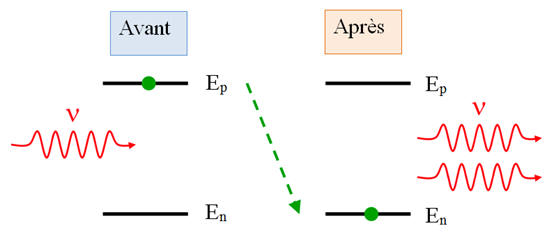
-   Un atome peut émettre spontanément un photon quand il passe d’un niveau d’énergie E_p à un niveau d’énergie inférieur E_n.

-   Ce phénomène est aléatoire.

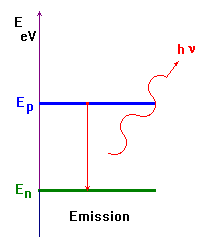
-   ΔE = E_p - E_n = h . ν

-   L’énergie quantifiée E de ce photon est telle que :

-   E = | E_p - E_n | = h . ν.

-   Cette émission a lieu de façon aléatoire dans n’importe quelle direction de l’espace.

-   L’émission spontanée fournit des photons incohérents entre eux.

-   Le but des physiciens était de contrôler cette émission spontanée.

3)- Émission stimulée.

-   En 1917, Albert Einstein prévoit un autre mode d’émission : l’émission stimulée.

-   Un atome excité émet un photon grâce à la stimulation que provoque l’arrivée d’un photon de même énergie que celui qu’il pourrait potentiellement émettre.

-   La particularité de ce type d’émission est que le photon stimulé prend strictement les mêmes caractéristiques (fréquence, direction et sens et phase) que le photon incident.

-   Comme si le second était la photocopie du premier.

-   Un photon incident d’énergie E = h . ν peut forcer un atome initialement dans un état excité d’énergie E_p, à passer au niveau d’énergie inférieur E_n.

-   Tel que : E_p - E_n = E =  h . ν

-   Ce passage s’accompagne de l’émission d’un second photon de même énergie, de mêmes sens et direction de propagation et de même phase que le photon incident.

-   Lors d’une émission stimulée, un photon incident interagit avec un atome initialement excité et provoque l’émission d’un second photon par cet atome.

-   L’énergie du photon incident doit être égale à la différence d’énergie entre les deux niveaux d’énergie de cet atome.

-   Deux photons sont obtenus après émission stimulée :

-   Le photon émis et le photon incident.

-   Ces deux photons ont :

-   Même fréquence,

-   Mêmes direction et sens de propagation,

-   Et même phase.

-   Ces photons peuvent à leur tour stimuler d’autres émissions du même type.

-   Ce processus est à la base du fonctionnement des lasers.

 

4)- Inversion de population.

-   Pour augmenter le nombre d’émissions stimulées, il faut qu’il y ait plus d’atomes dans un état excité que dans l’état fondamental.

-   Pour réaliser cette inversion de population, il faut transférer de l’énergie aux atomes concernés.

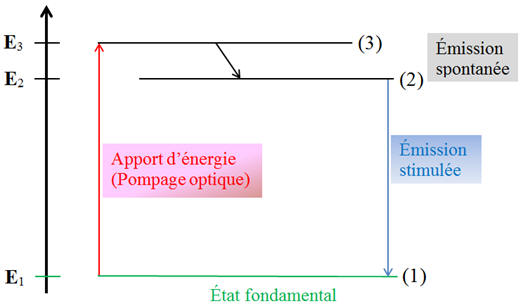
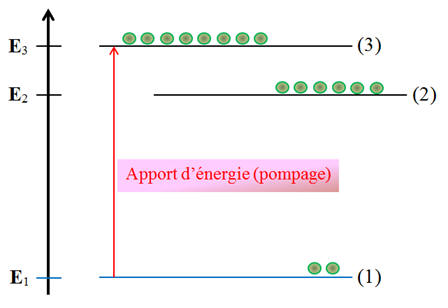
-   On apporte l’énergie nécessaire qui permet aux atomes de passer du niveau fondamental (1) au niveau excité (3) :

-   C’est ce que l’on appelle le pompage.

-   Les atomes ne restent pas au niveau (3).

-   Spontanément, ils redescendent au niveau (2) ou ils s’accumulent.

-   La transition du niveau (2) vers le niveau (1) peut se faire :

-   Lors d’une émission spontanée

-   Ou lors d’une émission stimulée.

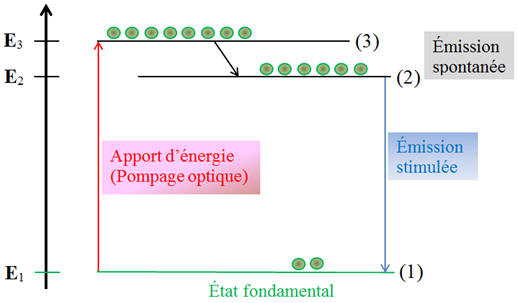
-   Schéma : Inversion de population

 

-   L’émission stimulée est favorisée par l’inversion de population.

-   L’inversion de population consiste à maintenir plus d’atomes dans un état excité que dans son état fondamental.

-   Un apport d’énergie est nécessaire pour provoquer cette situation.

5)- L’amplification.

-   Le milieu laser est constitué par des atomes capables d’émettre des photons par émission stimulée.

-   Ce milieu est placé entre deux miroirs disposés parallèlement face à face (cavité Fabry-Pérot).

-   Ces miroirs imposent des allers-retours aux photons.

-   Ce dispositif permet d’augmenter le nombre d’interactions photon-atome et donc le nombre de photons produits par émission stimulée.

-   L’ensemble constitue un oscillateur laser.

-   Une source d’énergie crée et maintient l’inversion de population dans le milieu laser.

-   Remarque :

-   Lors des allers-retours, les ondes associées aux photons vont interférer entre elles car elles sont cohérentes.

-   Pour qu’il n’y ait pas de perte d’intensité lumineuse, les interférences doivent être constructives.

-   Pour cela, dans le cas d’un milieu laser d’indice n = 1, la distance aller-retour entre les miroirs doit être un multiple entier de la longueur d’onde.

-   L’un des deux miroirs est partiellement transparent pour permettre de récupérer une partie du rayonnement produit par l’oscillateur.

 

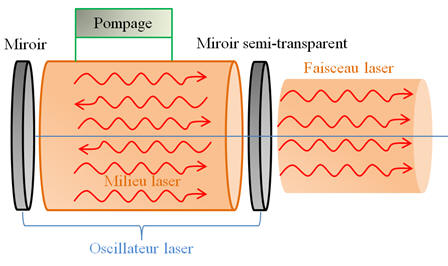
-   Un laser comprend :

-   Une cavité qui contient le milieu actif dans lequel a lieu l’émission de lumière.

-   Une source d’énergie extérieure pour entretenir l’émission.

-   Un ensemble de deux miroirs rigoureusement parallèles dont l’un est partiellement réfléchissant pour permettre l’émergence du faisceau laser.

-   Exemples de lasers :

6)- Principales propriétés du laser.

-   Un laser produit un faisceau lumineux monochromatique dont tous les photons sont en phase.

-   Un laser produit un faisceau lumineux cohérent.

-   Comme tous les photons se propagent dans la même direction et dans le même sens, le faisceau produit par un laser et très directif.

-   Un faisceau laser est :

-   Directif, intense, monochromatique et cohérent.

-   Il est très directif :

-   Le diamètre de la tache sur l’écran augmente très légèrement lorsque l’on éloigne celui-ci.

-   Il est peu divergent.

-   Ce sont des sources de lumière très intenses.

-   Par exemple, le laser hélium-néon a une puissance P ≈ 2,0 mW.

-   Le rayon du faisceau émis : r ≈ 0,40 mm.

-   La puissance par unité de surface :

-   .

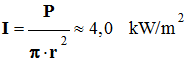-   Cette puissance est quatre fois supérieure à la puissance maximale du rayonnement solaire par unité de surface.

-   Les faisceaux lasers sont dangereux pour les yeux.

-   La lumière laser est monochromatique.

-   Elle ne peut pas être décomposée par un prisme ou un réseau.

-   Le laser émet dans le visible (400 nm ≤ λ ≤ 800 nm) ou dans l’infrarouge (1 μm ≤ λ ≤ 10 μm).

-   La lumière laser possède une grande cohérence spatiale et temporelle.

-   Le laser à impulsions :

-   Un laser à impulsions permet de concentrer dans le temps l’énergie grâce à des émissions de très courte durée.

-   Les lasers à impulsions permettent une concentration spatiale et temporelle de l’énergie.

-   La puissance des lasers peut aller du milliwatt (mW) au térawatt (TW : (1 TW = 10¹² W).

-   On les utilise :

-   Pour la lecture des codes-barres,

-   Pour la lecture des CD et DVD,

-   Pour le transport de l’information par fibre optique,

-   Pour la détermination de distances,

-   Pour le nettoyage de surfaces,

-   Pour la chirurgie,

-   …

-   Tableau :

7)- De la découverte à l’invention :

-   1917 : Publication d’Einstein

-   1928 : Mise en évidence de l’émission stimulée (preuve indirecte) par LADENBOURG et KOPFERMAN.

-   1949 : Réalisation du pompage optique KASTLER, prix Nobel en 1966.

-   1954 : Premier MASER à ammoniac (M pour MICROWAVE : MICROWAVE AMPLIFICATION BY STIMULATED EMISSION OF RADIATION) par TOWNES-GORDON-ZEIGER, ils ont pensé à la cavité résonnante. (microwave pour micro-onde)

-   Le maser émet un rayonnement dans le domaine radio à des longueurs d'onde de l’ordre du millimètre au mètre.

-   1960 Premier laser à rubis par MAIMAN (λ ≈ 694,3 nm)

-   Couleur :

 

III- Domaine spectral et transition électronique.

1)- Énergie d’une molécule.

-   Une molécule est constituée d’un nombre limité d’atomes qui vibrent les uns par rapport aux autres.

-   Elle possède de l’énergie vibratoire en plus de son énergie électronique liée à la répartition des électrons.

-   Ces deux énergies sont quantifiées.

-   Ces énergies ne peuvent prendre que certaines valeurs particulières caractéristiques de la molécule considérée.

-   On parle aussi de valeurs discrètes.

-   Pour la molécule, on définit aussi des niveaux d’énergie électronique.

-   À chaque niveau d’énergie électronique correspond des sous-niveaux d’énergie vibratoire.

-   Cas de la molécule d’eau :

-   Schématisation des différents modes de vibration de la molécule d’eau

 

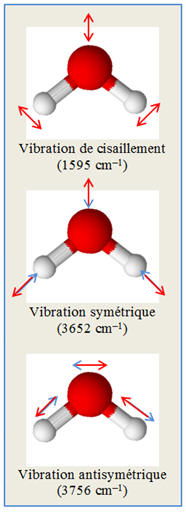
-   Schéma : niveaux d’énergie électronique d’une molécule et sous niveaux.

2)- Transitions énergétiques.

-   Une molécule peut passer d’un niveau d’énergie inférieur à un niveau d’énergie supérieur par absorption d’un quantum d’énergie.

-   Elle peut revenir à son état d’énergie inférieur en émettant un photon.

-   Ces transitions énergétiques sont des transferts quantiques d’énergie.

-   Une transition d’un niveau électronique à un autre nécessite plus d’énergie qu’une transition vibratoire.

-   Un domaine spectral est associé à chacune de ces transitions.

-   Une transition d’énergie électronique est associée à une radiation ultraviolette ou visible.

-   Une transition d’énergie vibratoire est associée à une radiation infrarouge.

 

IV- Applications.

1)- QCM : pour chaque question, indiquer la (ou les) bonne(s) réponse(s).

QCM sous forme de tableau. QCM réalisé avec le logiciel Questy pour s'auto-évaluer.

2)- L'effet Laser.

 

 

 

3)- Exercices : Exercices : énoncé avec correction

a)-   Exercice 8 page 390 : Créer une onde de matière avec un électron.

b)-  Exercice 10 page 390 : Connaître l’aspect probabiliste.

c)-   Exercice 11 page 390 : Utiliser un diagramme énergétique.

d)-  Exercice 14 page 391 : Associer transition et radiation.

e)-   Exercice 15 page 391 : étudier une transition.

f)-   Exercice 16 page 391 : Dualité ou non dualité.

g)-  Exercice 19 page 392 : Laser hélium-néon.

h)-  Exercice 20 page 391 : Fonctionnement du laser hélium-néon.

i)-    Exercice 26 page 394 : Les alcools en spectroscopie.

j)-    Exercice 27 page 394-395 : Valse laser à trois ou quatre temps.

k)-  Exercice 28 page 395 : Effet  photoélectrique.