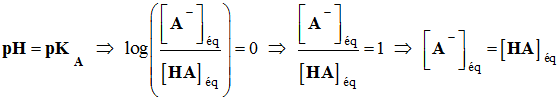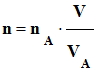|
Contrôle de qualité par dosage. Exercices. |
|
|
|
I-
Exercice 6 page 478 : Utiliser la loi de Beer-Lambert.
|
On dispose d’une échelle de teinte en diiode dont les concentrations C sont connues. Un spectrophotomètre, réglé sur la longueur d’onde λ = 450 nm, permet de mesurer l’absorbance A des
solutions de l’échelle des teintes. On peut alors
tracer le graphe
A =
f (C).
1)-
Comment appelle-t-on le graphe A = f (C) ? 2)-
La loi de Beer-Lambert est-elle vérifiée ? 3)- Sans modifier les réglages du spectrophotomètre, on mesure l’absorbance AS = 0,64 d’une solution S d’eau iodée. En déduire la concentration CS en diiode de la solution S. |
|
1)-
Le graphe A = f (C) :
- C’est la courbe
d’étalonnage. 2)-
La loi de Beer-Lambert :
- Les points sont
sensiblement alignés. La portion de droite obtenue
passe pratiquement par l’origine.
- L’absorbance A
est proportionnelle à la concentration C de
la solution pour les concentrations utilisées en
solutions de diiode.
- A = k .
C,
-
k
est le
coefficient directeur de la portion de droite tracée.
- La loi de
Beer-Lambert est vérifiée dans le domaine de
concentrations utilisées.
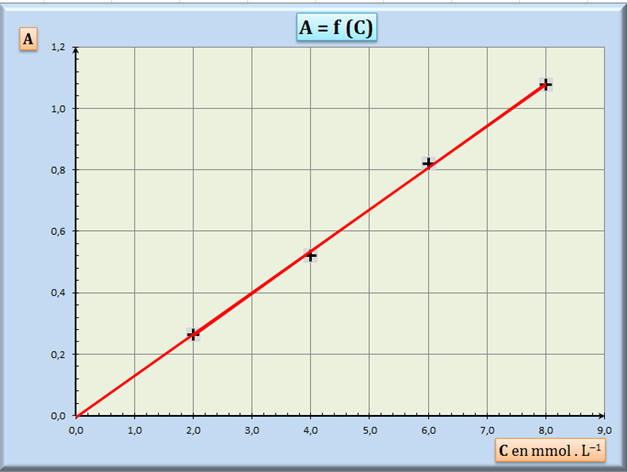
- On ajoute une courbe
de tendance : clic gauche sur la série utilisée :
- On choisit
« linéaire » et on coche « afficher l’équation sur
le graphique » et « afficher le coefficient de
détermination (R²) sur le graphique.
- Le coefficient de
détermination R2
≈ 0,9991 se rapproche de la valeur 1.
- Le modèle, qui a été
choisi, traduit bien les variations de l’absorbance
en fonction de la concentration. 3)-
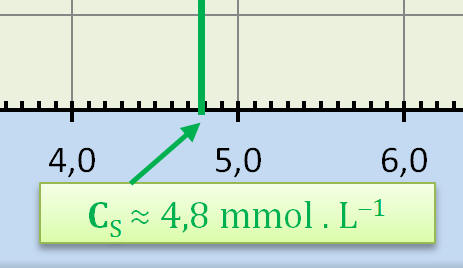
Concentration CS en diiode de la
solution S.
- CS
≈ 4,8 mmol . L–1. |
II-
Exercice 7 page 478 : Utiliser la loi de Kohlrausch.
|
La carence en élément calcium,
ou hypocalcémie, peut être traitée par injection
intraveineuse d’une solution de chlorure de calcium. On souhaite déterminer la concentration C0 en chlorure de calcium contenue dans une ampoule de 10,0 mL. Le contenu de l’ampoule est dilué 100 fois. La mesure de la conductivité de la solution S
obtenue est
σS = 1,23 mS . cm–1. On mesure également la
conductivité de différentes solutions étalon en
chlorure de calcium. Les résultats sont rassemblés
dans le tableau ci-dessous :
1)-
Tracer le courbe σ = f (C). 2)-
La loi de Kohlrausch est-elle vérifiée ? 3)-
En déduire les concentrations CS
et C0. |
|
1)-
Courbe σ = f (C). 2)- Loi de Kohlrausch :
-
Les points sont
sensiblement alignés. La portion de droite obtenue
passe pratiquement par l’origine.
-
La conductivité σ
est proportionnelle à la concentration C de
la solution pour les concentrations utilisées en
solutions de chlorure de calcium.
-
σ = k .
C,
-
k
est le
coefficient directeur de la portion de droite tracée.
-
La loi de Kohlrausch
est vérifiée dans le domaine de concentrations
utilisées.
-
Le coefficient de
détermination R2
≈ 0,9998 se rapproche de la valeur 1.
-
Le modèle
« Linéaire », qui a été choisi, traduit bien les
variations de la conductivité en fonction de la
concentration. 3)-
Valeurs des concentrations CS et
C0.
-
Valeur de la
concentration CS (Détermination
graphique) :
-
CS
≈ 4,6 mmol . L–1
-
Or C0
= 100 CS
-
C0
≈ 100
×
4,6
×
10–3
-
C0
≈ 0,46 mol . L–1 |
III- Exercice 8 page 478 : Utiliser une relation
d’équivalence.
|
Pour contrôler la composition complète d’une ampoule de complément alimentaire contenant des ions Fe2+ (aq), la solution qu’elle contient peut être dosée
par les ions
MnO4–
(aq) d’une
solution de permanganate de potassium de
concentration connue. L’équation support de la
réaction de titrage est :
MnO4–
(aq)
+
8
H+ (aq)
+
5
Fe2+ (aq)
→
Mn2+
(aq)
+
5
Fe3+ (aq)
+
4
H2O
(ℓ) 1)-
Quel est le réactif titrant ? Le réactif titré ? 2)-
Quelles doivent être les caractéristiques de la
réaction support du titrage ? 3)-
On note n0 (Fe2+)
et nE (MnO4–)
respectivement la quantité initiale d’ions Fe2+
(aq) à
doser et la quantité d’ions MnO4–
(aq) versée
à l’équivalence. a)-
Définir l’équivalence du
titrage. b)-
En déduire une relation
entre n0 (Fe2+)
et nE (MnO4–). |
|
1)-
Le réactif titrant et le réactif titré :
-
Réactif titrant : les
ions MnO4–
(aq)
-
Réactif titré : les
ions Fe2+ (aq) 2)-
Caractéristiques de la réaction support du titrage :
-
La réaction support
du titrage doit être totale, rapide et unique. 3)-
L’équivalence. a)-
Définition de l’équivalence
du titrage :
-
L’équivalence d’un
titrage est atteinte lorsque le réactif titrant et
le réactif titré sont dans les proportions
stœchiométriques.
-
Les deux réactifs
sont alors totalement consommés. Ils ont totalement
disparu.
-
À l’équivalence, les
réactifs sont dans les proportions stœchiométriques. b)-
Relation entre n0
(Fe2+) et nE (MnO4–)
à l’équivalence :
-
Relation à
l’équivalence :
-
n0
(Fe2+) = 5 nE (MnO4–) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
IV-
Exercice 14 page 480 : Choisir un indicateur coloré.
|
Une solution d’hydroxyde de
sodium est dosée par une solution d’acide
chlorhydrique, ajoutée à la burette graduée. Le
pH à
l’équivalence de ce titrage est
pHE
= 7,0. On dispose de trois indicateurs
colorés dont les teintes sont données ci-dessous :
1)-
Est-il possible de repérer l’équivalence du titrage
sans un indicateur coloré ? Si oui, comment ? 2)-
Choisir, en justifiant, l’indicateur coloré adapté à
ce titrage. 3)-
Comment repère-ton alors l’équivalence du titrage ? |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1)-
Repérer l’équivalence du titrage sans un indicateur
coloré :
-
La réaction qui se
produit, lors du titrage,
est la suivante :
H3O+
(aq) + HO–
(aq) → 2 H2O
(ℓ)
-
On peut réaliser un
titrage conductimétrique
ou un
titrage pH-métrique. 2)-
Choix de l’indicateur coloré adapté à ce titrage.
-
L’indicateur coloré
le mieux adapté pour le titrage est le Bleu de
bromothymol (B.B.T).
-
La valeur du pH
à l’équivalence appartient à sa zone de virage.
-
6,0 ≤
pHE
≤
7,6 - Avec l’hélianthine, le virage se fait juste avant l’équivalence, alors qu’avec la phénolphtaléine,
le virage a lieu juste
après l’équivalence. 3)-
Repérage de l’équivalence du titrage :
-
À l’équivalence, il y
a un changement de teinte de l’indicateur coloré,
ceci à la goutte près. |
V-
Exercice 16 page 481 : Titrage colorimétrique d’une eau
oxygénée.
|
On souhaite déterminer la
concentration
C0
en peroxyde d’hydrogène d’une solution commerciale
d’eau oxygénée. La réaction entre les ions permanganate MnO4– (aq) et le peroxyde d’hydrogène H2O2 (aq), appartenant aux couples oxydant / réducteur
MnO4–
(aq) /
Mn2+
(aq) et
O2
(g) / H2O2
(aq) sert de support au titrage. On dilue 10 fois la solution commerciale S0 : on obtient une solution S1. On titre un volume V1 = 10,0 mL de la solution S1 par une solution
S2
de permanganate de potassium de concentration
C2
= 0,020 mol . L–1. Le volume équivalent est
VE
= 17,6 mL. 1)-
Écrire l’équation de la réaction de titrage. 2)-
Sachant que l’ion MnO4–
(aq) est violet et qu’il est la seule espèce
colorée du système étudié, comment repère-t-on
l’équivalence du titrage ? 3)-
En s’aidant éventuellement d’un tableau
d’avancement, établir l’expression de la
concentration C1 en peroxyde
d’hydrogène de la solution S1. 4)-
Calculer la valeur des concentrations C1
et C0. 5)-
Calculer la quantité de matière de peroxyde
d’hydrogène n0 (H2O2)
présente dans un litre de solution commerciale S0.
-
L’eau oxygénée
étudiée est dite « à 10 volumes » ; cela signifie
qu’un litre de solution peut libérer 10 L de
dioxygène selon la réaction d’équation :
2 H2O2
(aq) → H2O
(ℓ) +
O2
(g) 6)-
En s’aidant éventuellement d’un tableau
d’avancement, calculer la quantité maximale nmax
(O2) de dioxygène libérée par la
solution S0. 7)- Dans les conditions de l’expérience, une mole de dioxygène occupe un volume égal à 22,4 L. En déduire
le volume de dioxygène maximal Vmax
(O2) libéré par un litre de
solution S0. 8)-
Comparer ce résultat à la valeur indiquée par le
fabricant en faisant un calcul d’incertitude
relative. |
|
1)-
Équation de la réaction de titrage :
-
Couple : MnO4-
(aq) /
Mn
2+
(aq)
-
Couple : O2 (aq) /
H2O2
(aq)
2)-
Repérage de l’équivalence.
-
Les ions permanganate
MnO4–
(aq) donnent une couleur violette
à la solution qui les contient
-
Lorsque l’on verse la
solution de permanganate de potassium dans la
solution d’eau oxygénée, les ions permanganate
disparaissent ainsi
que leur coloration.
-
Juste après
l’équivalence, la solution prend une teinte violette
caractéristique de la présence des ions
permanganate.
-
On peut repérer
l’équivalence grâce à la persistance de cette
coloration. 3)-
Expression de la concentration C1
en peroxyde d’hydrogène de la solution S1.
-
Tableau réduit :
-
4)-
Valeur des concentrations C1 et
C0.
-
Valeur de la
concentration C1 :
-
-
Valeur de la
concentration C0.
-
C0
= 10 C1
-
C0
≈ 0,88 mol . L–1. 5)-
Quantité de matière de peroxyde d’hydrogène n0
(H2O2) présente
dans un litre de solution commerciale S0.
-
n0
(H2O2) = C0
. V
-
n0
(H2O2) ≈ 0,88
mol 6)-
Quantité maximale nmax (O2)
de dioxygène libérée par la solution S0.
-
On l’équation de la
réaction :
2 H2O2
(aq) → H2O
(ℓ) +
O2
(g)
-
Tableau
d’avancement :
-
7)-
Volume de dioxygène maximal Vmax (O2)
libéré par un litre de solution S0.
-
Vmax
(O2) = nmax (O2)
. Vm
-
Vmax
(O2) ≈ 0,44
×
22,4 ≈ 9,856
-
Vmax
(O2) ≈ 9,9 L 8)-
Calcul d’incertitude relative :
-
-
Si on travaille avec
les calculs intermédiaires :
-
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
VI-
Exercice 18 page 481 : Retrouver la loi de Kohlrausch.
|
La conductivité
d’une solution est donnée par la relation :
On considère une solution de
concentration
C en
chlorure de magnésium apporté. 1)-
Écrire l’équation de dissolution du chlorure de
magnésium, MgCl2 (s), dans l’eau. 2)-
Exprimer les concentrations ioniques [Mg2+]
et [Cl–] dans la solution en
fonction de la concentration C. 3)-
Écrire l’expression de la conductivité
σ de cette solution en fonction de la
concentration C et des conductivités ioniques
molaires. 4)-
Montrer que la loi de Kohlrausch est vérifiée. |
|
1)- Équation de dissolution du chlorure de magnésium, MgCl2 (s), dans l’eau.
2)-
Concentrations ioniques [Mg2+] et
[Cl–] dans la solution en fonction
de la concentration C.
-
Tableau
d’avancement :
-
-
3)-
Expression de la conductivité
σ de cette solution en fonction de la
concentration C et des conductivités ioniques
molaires.
-
σ
= λ (Mg2+).[
Mg2+
] + λ
(Cl–).[
Cl–
]
-
σ
= λ
(Mg2+).C
+ 2 λ (Cl–)
.
C
-
σ
= {λ
(Mg2+)
+ 2 λ (Cl–)}
.
C 4)- Loi de
Kohlrausch : - Les conductivités molaires ioniques sont des grandeurs caractéristiques des ions.
- Ce sont des constantes à
une température donnée.
-
λ
(Cl–)
= 7,63
×
10– 3 S.m2.mol– 1 à 25 °C
dans l’eau
-
λ
(Mg2+)
= 10,6
×
10– 3 S.m².mol–1
à 25 °C dans l'eau
-
Le terme
{λ (Mg
2+)
+ 2 λ (Cl
–)}
= cte = k
-
En conséquence :
-
σ
=
k.
C
-
La loi de
Kohlrausch est vérifiée. |
||||||||||||||||||||||||||||||||||||||
VII- Exercice 21 page 483 : Chaufferette chimique.
|
Une chaufferette
chimique est constituée d’une enveloppe souple de
pastique qui contient une solution d’éthanoate de
sodium à 20 % minimum en masse. Lorsqu’on appuie sur un petit
disque métallique placé à l’intérieur, le liquide
commence à se solidifier tout en dégageant de la
chaleur. Après utilisation, on peut
régénérer la chaufferette en faisant fondre le
solide obtenu par chauffage. -
Données relatives à l’éthanoate de
sodium CH3COONa : -
Masse molaire : M = 82,0 g .
mol–1 ; -
Solubilité : à 25 ° C dans l’eau :
s = 365 g . L–1 soit 4,5 mol . L–1. La solution
aqueuse S0 d’éthanoate de sodium,
Na+ (aq) + CH3COO–
(aq), d’une chaufferette, a un volume V0 = 100
mL et une masse m = 130 g. La solution S0 étant trop concentrée pour être dosée directement au laboratoire, on prépare une solution S1 en diluant 100 fois le contenu de la chaufferette. Pour déterminer la concentration molaire C0 en éthanoate de sodium apporté dans une chaufferette chimique, on place dans un bécher un volume V1
= 25,0 mL de la solution S1 à
titrer. On réalise un titrage
pH-métrique par une solution d’acide chlorhydrique,
H3O+ (aq) +
Cl– (aq), de concentration CA
= 2,0
× 10–1 mol . L–1. On note VA le
volume de solution d’acide chlorhydrique versé. L’équation de la réaction
support du titrage s’écrit : CH3COO–
(aq) + H3O+
(aq) → CH3COOH
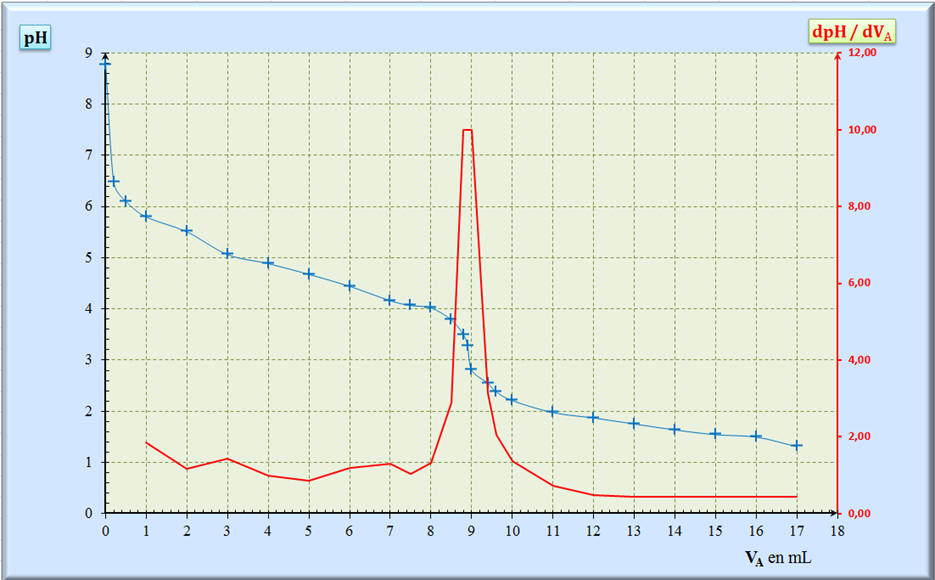
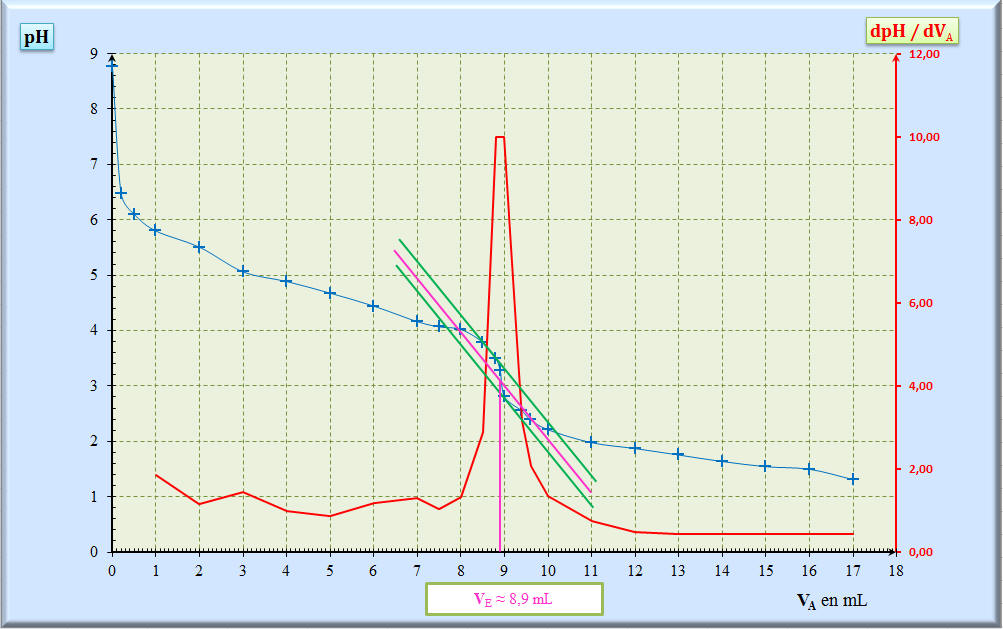
(aq) + H2O (ℓ) On obtient la courbe ci-après :
1)- Schématiser et légender le dispositif de
titrage. 2)- Après avoir défini l’équivalence, écrire la relation entre la quantité d’ions éthanoate ni (CH3COO–) présente initialement dans le bécher et la quantité d’ion oxonium nE (H3O+) qui permet d’atteindre l’équivalence. On pourra
éventuellement s’aider d’un tableau d’avancement. 3)- Déterminer le volume équivalent VE
en expliquant la méthode utilisée. 4)- Des titrages successifs ont donné les valeurs suivantes du volume à l’équivalence : -
8,8 mL ; 8,6 mL ; 9,0 mL ; 6,3 mL ;
8,9 mL ; 9,1 mL ; 8,8 mL ; 8,7 mL. - Après avoir supprimé la(les) valeur(s) aberrante(s), réaliser une étude statistique des résultats expérimentaux et donner un encadrement de
la valeur du volume à l’équivalence VE. 5)- À partir de la valeur moyenne de VEmoy
déterminée à la question 4)-, calculer la
concentration C1 en ions éthanoate
de la solution dosée. 6)- En déduire la concentration C0 en éthanoate de sodium apporté dans la solution contenue dans la chaufferette. La solution
d’éthanoate de sodium contenue dans la chaufferette
est-elle saturée ? 7)- Calculer la masse d’éthanoate de sodium dans
la chaufferette. 8)- La solution aqueuse de masse 130 g contenue dans la chaufferette est-elle au moins à 20 % en
masse d’éthanoate de sodium comme l’indique le texte
introductif ? |
|
1)- Dispositif de titrage : 2)- Étude de l’équivalence : -
Définition :
-
L’équivalence d’un titrage est
atteinte lorsque le réactif titrant et le réactif
titré sont dans les proportions stœchiométriques. -
Les deux réactifs sont alors
totalement consommés. Ils ont totalement disparu. -
Tableau d’avancement :
CH3COO–
(aq) + H3O+
(aq) → CH3COOH
(aq) + H2O (ℓ)
-
Relations : -
ni (CH3COO–)
= nE (H3O+) -
C1 . V1
= CA . VE 3)- Volume équivalent VE en
expliquant la méthode utilisée -
Méthode des tangentes :
-
Méthode de la courbe dérivée :
-
En conséquence : VE
≈ 8,9 mL -
Tableau de valeurs :
4)- Étude statistique : Encadrement de la valeur du volume à l’équivalence V E.-
8,8 mL ; 8,6 mL ; 9,0 mL ; 6,3 mL ;
8,9 mL ; 9,1 mL ; 8,8 mL ; 8,7 mL. -
Valeur erronée : VE
= 6,3 mL -
On peut calculer la valeur moyenne et
l’écart-type. -
La moyenne arithmétique est le
quotient de la somme des valeurs
x
i par le nombre
n. -
On écrit :
-
La variance
var est
le quotient de la somme des carrés des écarts à la
moyenne par le nombre
n de
l’effectif total. -
-
Détermination de la variance de
l’échantillon :
-
L’écart-type σ
: C’est la racine carrée de la variance : -
Si représente la moyenne,
σ l‘écart-type et x une
valeur incluse dans l'ensemble de données, alors -
environ
68 % des données se situent à l'intérieur de
l'intervalle :
-
environ
95 % des données se situent à l'intérieur de
l'intervalle :
-
Environ 99 % des données se situent à
l'intérieur de l'intervalle :. -
Détermination de l’écart-type :
-
Pour un intervalle de confiance de 95
%, on obtient l’encadrement suivant : (8,84 – 2
x 0,16) mL ≤ VE
≤ (8,84 + 2
x 0,16) mL 8,52 mL ≤
VE ≤ 9,16 mL 5)- Concentration C1 en ions
éthanoate de la solution dosée : -
Relation à l’équivalence : C1
. V1 = CA . VEmoy -
6)- Concentration C0 en
éthanoate de sodium apporté dans la solution
contenue dans la chaufferette : -
C0 = 100 C1 -
C0 ≈ 7,1 mol . L–1 -
On donne la solubilité de la solution
d’éthanoate de sodium : -
Solubilité : à 25 ° C dans l’eau :
s = 365 g . L–1 soit 4,5 mol . L–1 -
Comme C0 > s,
la solution est saturée. 7)- Masse m0 d’éthanoate de
sodium dans la chaufferette : -
Données : -
La solution aqueuse S0
d’éthanoate de sodium, Na+ (aq) +
CH3COO– (aq),
d’une chaufferette, a un volume V0 = 100
mL et une masse m = 130 g. -
Masse molaire de l’éthanoate de
sodium : M = 82,0 g . mol–1 -
m0 = n0
. M
-
La quantité de matière n
d’éthanoate de sodium est donnée par la relation : -
n0 = C0
. V0
-
En conséquence :
-
m0 = C0
. V0 . M -
m0 ≈ 7,1
× 100
× 10–3× 82,0 -
m0 ≈ 58 g 8)- Pourcentage en masse d’éthanoate de sodium : -
La masse d’éthanoate de sodium
présente dans la chaufferette est m0
≈ 58 g -
La masse de la solution est m =
130 g : -
Pourcentage massique en éthanoate de
sodium de la solution présente dans la
chaufferette : -
- La teneur en éthanoate de sodium de la chaufferette est d’environ 45 %. - Cette valeur est
très supérieure à la valeur de 20 % minimale
annoncée dans le texte. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
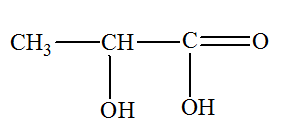
VIII- Exercice 24 page 485 : Titrage de l’acide lactique
dans le lait.
|
En vieillissant,
le lactose présent dans le lait se transforme en
acide lactique, noté par la suite
HA. On dose l’acide lactique, considéré comme le seul acide présent dans le lait étudié, par une solution d’hydroxyde de sodium ou
soude, Na+
(aq) + HO–
(aq), de concentration
CB
= 5,00
× 10–2 mol . L–1. On prélève un volume
VA
= 20,0 mL de lait que l’on place dans un bécher et
on suit l’évolution du
pH en
fonction du volume
VB
de soude versé. On obtient les valeurs données
dans le tableau suivant :
On note
VE
le volume de soude versé à l’équivalence du titrage. Un lait frais a
une concentration en acide lactique inférieure à 1,8
g . L–1.
-
Données :
-
Couples acide-base :
-
H2O
(ℓ) / HO– (aq), pKA1
= 14,0
-
H3O+
(aq) / H2O (ℓ), pKA2
= 0,0
-
HA (aq) / A–
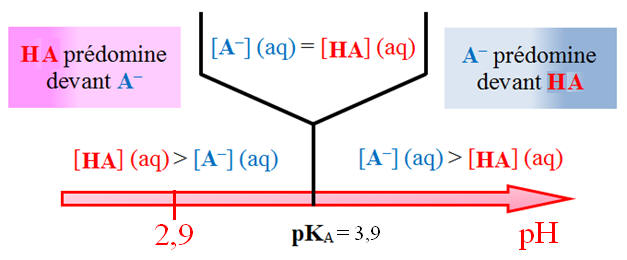
(aq), pKA3 = 3,9
-
Masse molaire de
l’acide lactique : M (HA) = 90,0 g .
mol–1.
-
Additif : acide
lactique :
Acide
2-hydroxypropanoïque :
-
1)-
Écrire l’équation de la réaction du titrage
réalisé : 2)-
Quelles caractéristiques doit présenter cette
réaction pour être adaptée à un dosage ? 3)-
En utilisant un diagramme de prédominance,
déterminer quelle est, entre HA (aq) et A–
(aq), l’espèce chimique prédominante au début du
dosage. 4)-
Pour quel volume de soude versé, noté VS,
les espèces HA (aq) et A–
(aq) sont-elles présentes en quantités égales dans
le bécher ? 5)-
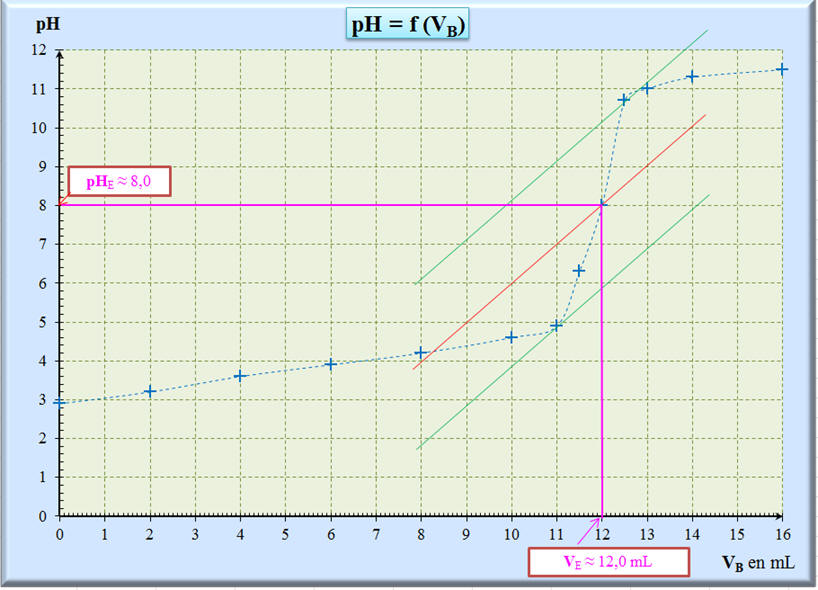
Tracer le graphe pH = f (VB).
En déduire la valeur du volume de soude versé à
l’équivalence VE. 6)-
Déterminer la quantité d’acide lactique présente
dans le volume VA de lait. 7)-
Quelle est la masse d’acide lactique présente dans
un litre de lait. Conclure. |
|
1)-
Équation de la réaction du titrage réalisé :
-
La réaction fait
intervenir l’acide lactique et la soude,
c’est-à-dire les couples acide / base :
-
H2O
(ℓ) / HO– (aq) et HA (aq) /
A– (aq)
HA
(aq) +
HO–
(aq)
®
A– (aq)
+
2)-
Caractéristiques de cette réaction pour être adaptée
à un dosage :
-
La réaction support
du dosage doit être totale, rapide, unique. 3)-
Diagramme de prédominance :
-
Au début du dosage,
pH = 2,9.
-
L’espèce qui
prédomine est l’espèce acide
HA
(aq) car pH < pKA3. 4)-
Volume de soude versé, noté VS,
pour que les espèces HA (aq) et A–
(aq) soient présentes en quantités égales dans le
bécher :
-
pH = pKA3
= 3,9 pour VS = 6,0 mL 5)-
Graphe pH = f (VB)
et valeur du volume de soude versé à l’équivalence
VE :
-
On utilise la méthode
des tangentes :
-
Volume de soude versé
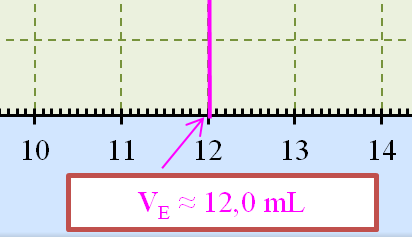
à l’équivalence VE :
-
VE
= 12,0 mL 6)-
Quantité d’acide lactique présente dans le volume
VA de lait.
-
Tableau
d’avancement :
-
nA
= xE
=
CB .VE
-
nA
≈ 5,00
× 10–2
× 12
× 10–3
-
nA
≈ 6,0
× 10–4 mol 7)- Masse
d’acide lactique présente dans un litre de lait et
Conclusion :
-
Quantité de matière
d’acide lactique présente dans un litre de lait :
-
-
Masse d’acide
lactique présente dans un litre de lait :
-
m = n .
M (HA)
-
-
Le lait analysé n’est
pas frais car sa teneur en acide lactique est
supérieure à 1,8 g . L–1. |
||||||||||||||||||||||||||||||||
|
|










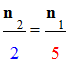 ou
ou
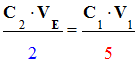

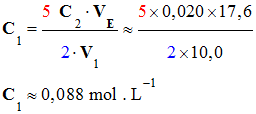
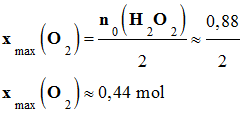
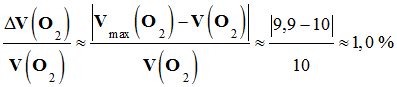

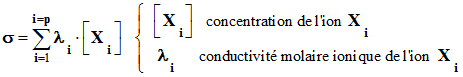
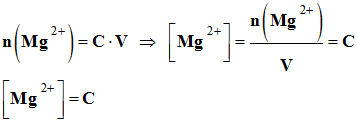



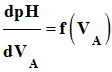 :
:





 ou
ou