QCM 01 Sous Forme de tableau. QCM 01 réalisé avec le logiciel Questy : Pour s'auto-évaluer. QCM 02 Sous Forme de tableau. QCM 02 réalisé avec le logiciel Questy : Pour s'auto-évaluer. QCM N° 02 Révisions QCM N° 02  Questy Révisions

 

Exercices :  énoncé avec correction a)-  Exercice 6 page 229. Connaître l’énergie cinétique. b)-  Exercice 7 page 229. Calculer une énergie cinétique. c)-  Exercice 8 page 229. Connaître l’énergie potentielle. d)-  Exercice 9 page 229. Calculer une énergie potentielle de pesanteur. e)-  Exercice 11 page 230. Étudier le freinage d’une voiture. f)-  Exercice 15 page 230. Chute de la pomme. g)-  Exercice 20 page 232. Le lancer du poids. h)-  Exercice 20 page 232. Expérience de Joule. i)-  Exercice 22 page 233. Pendule simple et énergie. j)-  Exercice 24 page 233 Transferts thermiques. k)-  Exercice 26 page 235. Freiner en scooter.

 

I- Les différentes formes d’énergie. (Chap. N° 07 L’énergie)

1)- Introduction.

-  Aux diverses interactions fondamentales, on peut associer des formes d’énergie.

-  Tout ce qui vie fonctionne, évolue, nécessite de l'énergie.

-  Le concept d'énergie est un concept abstrait, très récent qui est employé aujourd'hui dans des domaines très variés qui dépassent le cadre de la mécanique classique.

-  Dans la vie de tous les jours, on entend parler de différents types d'énergie :

-  L'énergie électrique, l'énergie calorifique, l'énergie lumineuse, l'énergie mécanique.

-  En conséquence, il existe différents types d'énergie.

-  D'autre part, on sait transformer une énergie en d'autres types énergies :

-  L'énergie électrique peut être convertie en énergie lumineuse, en énergie calorifique, en énergie mécanique suivant le convertisseur utilisé.

-  Toutes ces formes d’énergie ne sont en fait que différentes manifestations d’une seule et unique grandeur physique :

-  L'énergie.

-  il faut attendre le XIX siècle et les travaux de Joule pour établir une relation entre le ralentissement du mouvement d’un corps sous l’effet de frottements

et l’accroissement de la température à la surface de contact et l’interpréter comme la transformation de l’énergie mécanique en énergie calorifique.

-  L’élément qui était censé être responsable des phénomènes calorifiques pour les scientifiques de cette époque s'appelait le phlogistique.

-  On doit à Lavoisier l’interprétation des phénomènes de combustion comme des réactions d’oxydation et ainsi la fin de la théorie du phlogistique.

-  Le phlogistique éliminé, il restait à réinterprété la nature de la chaleur, ce que Joule réalisa en montrant l’équivalence entre l’énergie mécanique et l’énergie calorifique.

-  À l’époque de Newton et de Leibniz, le concept et le mot " énergie " tels que nous les connaissons n’existaient pas.

-  Leibniz introduisit une grandeur physique qu’il baptisa " action pure " - dénommée aujourd’hui " travail " qui devait jouer un rôle fondamental dans la construction du concept d’énergie.

 

2)- L’énergie liée à la vitesse.

►  Solide en translation rectiligne :

-  Un solide est en mouvement de translation, par rapport à un référentiel R, si le vecteur défini par deux points quelconques A et B du solide garde la même direction, le même sens et la même valeur au cours du mouvement.

-  Tous les points du solide ont, à chaque instant, le même vecteur vitesse.

-  Tous les points du solide ont, à chaque instant, la même vitesse.

-  Les point A, B, C,…. se déplacent à la même vitesse v, on dit que le solide se déplace à la vitesse v.

-  C’est aussi bien la vitesse v du centre d’inertie G du solide que celle d’un point quelconque du solide.

 

-  L'énergie cinétique E_C d'un système, par rapport à un référentiel donné, est l'énergie liée à son mouvement par rapport à ce référentiel.

-  On considère le système dans son ensemble.

-  On étudie en classe de première le cas d'un système animé d'un mouvement de translation.

 

►  Définition :

-  L’énergie cinétique E_C d’un solide en mouvement de translation est égale au demi-produit de la masse m du solide par le carré de la vitesse v² du solide.

-  On écrit :

-   

-  Unités :

-  L’énergie cinétique caractérise un solide en mouvement.

-  Elle est :

-  Proportionnelle à la masse m du solide

-  Proportionnelle au carré de la vitesse v du solide.

-  Elle dépend du référentiel d’étude.

-  C’est une grandeur supérieure ou égale à zéro.

 

3)- L’énergie liée à l’altitude.

-  L’énergie potentielle de pesanteur E_p d’un solide est l’énergie qu’il possède du fait de sa position par rapport à la Terre, c’est-à-dire du fait de son altitude.

-  Un solide de masse m est soumis à son poids 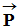 sur la Terre.

-  L’énergie potentielle de pesanteur d’un solide est l’énergie qu’il possède du fait de son interaction avec la Terre.

-  La valeur de cette énergie dépend de la position du solide par rapport à la Terre.

-  Expression : E_p = m . g . z.

-  Remarque 1 :

-  La valeur de l’énergie potentielle de pesanteur dépend de la valeur de z.

-  Elle dépend du choix de l’origine des altitudes.

-  L’énergie potentielle est définie à une constante additive près.

-  La différence d’énergie potentielle ne dépend pas du choix de l’origine.

-  Pour les exercices, on choisit l’origine la plus commode, celle qui simplifie les calculs.

 

-  On choisit de façon arbitraire : Ep (O) = 0

-  Le solide S de masse m, à l’altitude z_A possède l’énergie potentielle de pesanteur :

-  E_p (A) = m . g . z_A

-  Le solide S de masse m, à l’altitude z_B possède l’énergie potentielle de pesanteur :

-  E_p (B) = m . g . z_B

-  Si on choisit comme origine des énergies potentielles la position z_B = 0

-  E_p (B) = m . g . z_B = 0

4)- Énergie mécanique d’un solide.

-  L’énergie mécanique d’un solide est la somme de son énergie cinétique et de son énergie potentielle.

-  Relation :

-  E_m = E_C +  E_P.

-  Unité : joule (J)

II- Exploitation du principe de conservation de l’énergie.

1)- Principe de conservation de l’énergie.

a)-  Système isolé :

-  Un système est isolé si aucun transfert d'énergie n'est possible entre le système et le milieu extérieur.

b)-  Principe de la conservation de l’énergie.

-  L’énergie d’un système isolé ne peut être ni détruite, ni créée.

-  L'énergie d'un système isolé se conserve, elle est constante.

-  Remarque :

-  Il peut se produire des transferts d'énergie à l'intérieur du système isolé, mais l'énergie totale du système reste la même.

 

2)- Cas de la chute libre. TP Physique N° 07

a)-  Définition :

-  Un solide en chute libre est un solide qui n’est soumis qu’à l’action de son poids.

-  Ainsi, on peut négliger la poussée d’Archimède et les forces de frottements (ceci tant que sa vitesse de déplacement n’est pas trop élevée).

-  Dans ce cas,

-  Une balle de masse m tombe en chute libre d’une hauteur h.

-  Si la balle est en chute libre sans vitesse initiale, on trouve la relation suivante :

-  v² = 2 g . h.

 

b)-  Expérience :

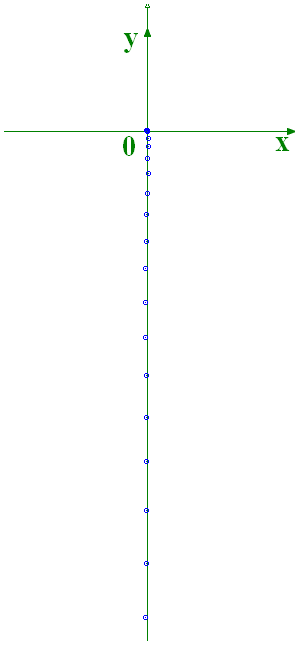
-  On filme, à l’aide d’une WebCam, la chute d’une balle de golf de masse m = 44 g.

 

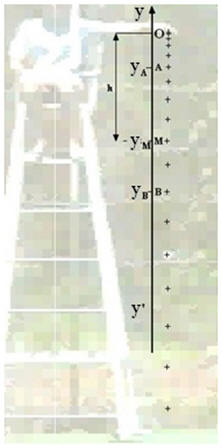
-  Tableau de valeurs et pointages :

-  On réalise les pointages à l’aide du logiciel AVIMECA 2.7.

 

-  Les propriétés du clip sont les suivantes :

 

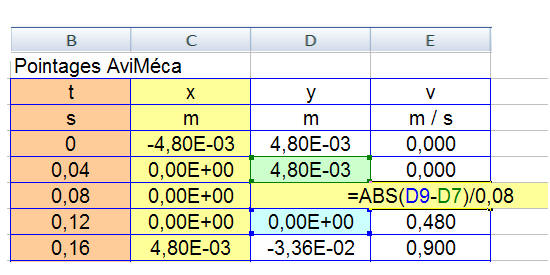
-  Pour connaître la valeur de la vitesse à chaque instant à l’aide du tableur, on calcule la vitesse moyenne pendant un intervalle de temps très court (ici 80 ms) encadrant l’instant considéré :

 

-  On utilise la colonne E pour l’étude de la vitesse da bille.

-  On prend modèle sur les autres colonnes pour la mise en forme.

-  La vitesse initiale (au temps t = 0 s) : on lâche la balle sans vitesse initiale : la vitesse initiale est nulle.

-  Pour calculer la valeur de la vitesse du point N° 2, on utilise la méthode déjà utilisée :

-  On calcule la vitesse moyenne pendant un intervalle de temps très court encadrant l’instant considéré :

-  On tape la formule suivante dans la cellule E8 : = ABS (D9 – D7) / 0,08

-  Le signe égale : pour signifier à Excel que l’on tape une formule

-  ABS () car on calcule la valeur de la vitesse qui est une grandeur positive

-  L’intervalle de temps vaut 2 t = 80 ms.

-  On recopie cette formule vers le bas autant que nécessaire avec la souris (copier – glisser)

-  On représente sur un même graphe, les variations de l’énergie cinétique, de l’énergie potentielle et le l’énergie mécanique en fonction du temps.

-  On choisit comme origine de l’énergie potentielle la position initiale de la balle.

-  Tableau de valeurs :

 

-  Graphe 1 : v = f (t)

 

-  Dans le cas présent, on a enlevé les deux premières images du clip.

-  La vitesse augmente avec la durée de chute.

-  C’est une fonction linéaire du temps :

-  v ≈ 9,89 t.

-  Graphe 2 : E = f (t)

 

►  Remarque :

-  L’énergie cinétique augmente au cours du temps, l’énergie potentielle diminue au cours du temps, alors que l’énergie mécanique se conserve au cours du temps.

►  Conclusion :

-  L’énergie mécanique d’un solide en chute libre est constante, elle se conserve :

-  ΔE_m = 0

 

3)- Application 1 : Chute avec frottements. TP Physique N° 08

a)-  Expérience :

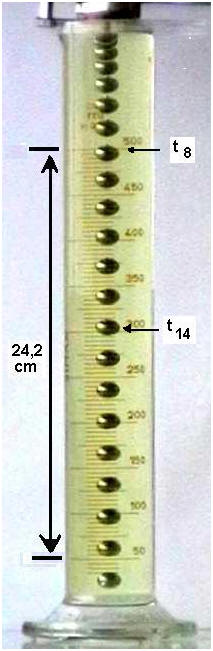
-  On filme, à l’aide d’une WebCam la chute d’une bille dans l’huile contenue dans une éprouvette graduée de 1 L.

-  On obtient le fichier : bille50

-  Données :

-  Propriétés du clip :

 

 

Vidéo : bille50.zip

b)- Exploitation :

-  Tableau de valeurs :

-  Graphe 1 : v = f (t).

 

-  Dans un premier temps, la vitesse de la bille augmente au cours du temps, son énergie cinétique augmente aussi.

-  Dans un deuxième temps, la vitesse de la bille se stabilise pour atteindre une valeur limite :

-  v_lim ≈ 0,94 m / s

-  De même que son énergie cinétique.

-  Graphe 2 : E = f (t).

-  Tableau de valeurs :

 

-  On remarque qu’au cours de la chute de la bille :

-   L’énergie cinétique du système augmente puis se stabilise.

-   L’énergie potentielle de pesanteur diminue.

-  L’énergie mécanique du système diminue aussi.

-  En conséquence, l’énergie mécanique de la bille ne se conserve pas.

►  Conclusions :

-  Un solide en chute dans un fluide est soumis à des frottements exercés par le fluide.

-  Son énergie mécanique diminue au cours de la chute.

-  De l’énergie est transférée de la bille vers le fluide.

-  Lorsqu’un solide chute avec frottements, une partie de son énergie mécanique est :

-  Soit transférée à un autre système,

-  Soit transformée en une autre forme d’énergie.

-  Ceci découle du principe de conservation de l’énergie.

 

4)- Application 2 : Transfert thermique.

TP Physique N° 09

►  Expérience : Mesure de la capacité thermique du laiton.

-  Lorsqu’un corps chaud et un corps froid, isolés du milieu extérieur, sont en contact l’un avec l’autre, il y a transfert thermique spontané du corps chaud vers le corps froid.

-  Ce transfert s’accompagne de variation de température ou de changement d’état.

-  Dans le cas d’un système isolé, le gain d’énergie de la partie froide du système est égal à la perte d’énergie de la partie chaude du système.

 

5)- Application 3 : La radioactivité β^–.

-  Cette radioactivité se manifeste lorsque le noyau présente un excès de neutrons.

-  Au cours de la désintégration, il y a émission :

-  D’un électron noté .

-  Équation de la transformation radioactive :

 

-  L’application du principe de conservation de l’énergie conduit à une énergie libérée :

-  E_lib = |Δm| . c² = |m_Y + m_e - m_X|. c²

-  Dans le référentiel lié au noyau Y, cette énergie est intégralement cédée à l’électron sous forme d’énergie cinétique.

-  En 1914, des mesures faites sur un grand nombre de désintégrations β^–, montrent que l’énergie cinétique acquise par l’électron n’est qu’une fraction variable de l’énergie disponible.

-  En 1930, Wolfgang PAULI postule l’existence d’une autre particule non détectée par les instruments de l’époque qui est émise lors de cette désintégration.

-  Cette particule permet d’expliquer la conservation de l’énergie et de la quantité de mouvement lors de cette transformation.

-  Cette particule neutre, de masse si faible (m_ν < 0,23 eV/c²) que l’on ne peut pas la détecter, a été baptisée neutrino (le petit neutre) par Enrico FERMI.

-  Écriture symbolique du neutrino :

-  Le neutrino a été découvert expérimentalement en 1956, par Frederick Reines et Clyde Cowan, auprès d’un réacteur nucléaire.

-  Remarque :

-  L’antineutrino  est l’antiparticule du neutrino.

-  Équation de la transformation radioactive :

 

III- Applications.

1)- QCM : Pour chaque question, indiquer la (ou les) bonne(s) réponse(s).

QCM 01 Sous Forme de tableau. QCM 01 réalisé avec le logiciel Questy : Pour s'auto-évaluer. QCM 02 Sous Forme de tableau. QCM 02 réalisé avec le logiciel Questy : Pour s'auto-évaluer. QCM N° 02 Révisions QCM N° 02  Questy Révisions

 

2)- Exercices :  Exercices :  énoncé avec correction

a)-  Exercice 6 page 229. Connaître l’énergie cinétique.

b)-  Exercice 7 page 229. Calculer une énergie cinétique.

c)-  Exercice 8 page 229. Connaître l’énergie potentielle.

d)-  Exercice 9 page 229. Calculer une énergie potentielle de pesanteur.

e)-  Exercice 11 page 230. Étudier le freinage d’une voiture.

f)-  Exercice 15 page 230. Chute de la pomme.

g)-  Exercice 20 page 232. Le lancer du poids.

h)-  Exercice 20 page 232. Expérience de Joule.

i)-  Exercice 22 page 233. Pendule simple et énergie.

j)-  Exercice 24 page 233 Transferts thermiques.

k)-  Exercice 26 page 235. Freiner en scooter.*