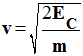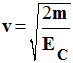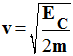|
QCM N° 13 |
Principe de conservation de l'énergie |
|
|
|
|
|
Énoncé |
A |
B |
C |
R |
|
1 |
L’énergie électrique est associée à l’interaction : |
Gravitationnelle |
Électromagnétique |
Forte / Faible |
B |
|
2 |
L’énergie nucléaire est associée à l’interaction : |
Gravitationnelle |
Électromagnétique |
Forte / Faible |
C |
|
3 |
L’énergie cinétique d’un solide
est liée : |
À son altitude |
À sa masse |
À la valeur de
la vitesse |
BC |
|
4 |
L’énergie potentielle de pesanteur d’un solide de masse m à l’altitude h s’écrit : |
2 m . g . h |
m . g . h |
½ m . g . h |
B |
|
5 |
La valeur de la vitesse d’un solide de masse m est liée à son énergie cinétique EC par la relation : |
|
|
|
A |
|
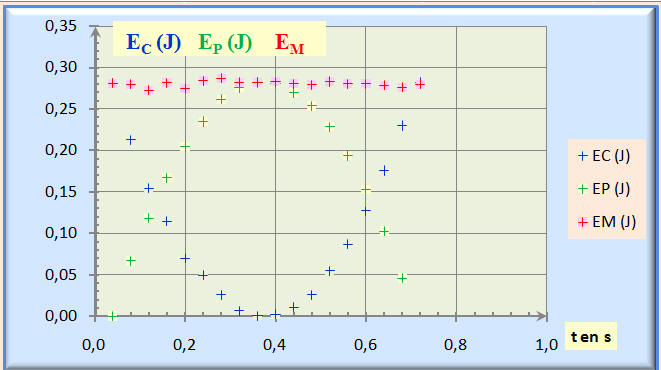
On a représenté ci-contre les énergies d’une balle lancée dans un champ de
pesanteur uniforme |
|||||
|
6 |
On considère le graphique ci-dessus.L’énergie qui se conserve est : |
L’énergie cinétique |
L’énergie potentielle de pesanteur |
L’énergie mécanique |
C |
|
7 |
Quand l’énergie cinétique diminue : |
L’énergie potentielle de pesanteur augmente |
L’énergie mécanique augmente |
L’énergie mécanique reste constante |
AC |
|
8 |
L’étude énergétique de ce mouvement montre que : |
Le poids de la balle est négligeable |
Les forces de frottement sont négligeables |
La balle est en
chute libre |
BC |
|
9 |
Lorsqu’un système est isolé, ce
système : |
Reçoit de l’énergie du milieu extérieur |
Cède de l’énergie au milieu extérieur |
N’effectue aucun échange avec le milieu extérieur |
C |
|
10 |
Un transfert thermique s’effectue spontanément : |
Du corps chaud vers le corps plus froid |
Du corps le plus froid vers le corps le plus chaud |
Dans les deux
sens |
A |
|
11 |
L’énergie cinétique d’une luge de masse m = 25,0 kg dont la vitesse est v = 36,0 km / h est de : |
1,62
× 104
J |
1,25
× 104
J |
1,25
× 103
J |
C |
|
12 |
On donne g = 10 N / kg. L’énergie potentielle de pesanteur étant choisie comme nulle au niveau de la mer, celle d’un plongeur de masse m = 100 kg à la profondeur h = 10 m, a pour valeur : |
1,0 kJ |
1,0
× 104
J |
–10 kJ |
C |
|
13 |
Pour que l’énergie cinétique d’un solide soit multipliée par 4, il faut que la vitesse soit multipliée par : |
2 |
4 |
16 |
A |
|
14 |
Deux objets ponctuels A et B en interaction avec la Terre sont à la même altitude. Les vitesses de A et de B sont liées par la relation vA = 2 vB et les masses par mB = 4 mA . Leurs énergie cinétique, potentielle et mécanique sont telles que : |
EC
(A) = EC (B) |
EP
(A) = EP (B) |
EM
(A) = EM (B) |
A |
|
15 |
On donne g = 10 N / kg. Pour une bille de masse m = 5,0 g chutant librement sans vitesse initiale, d’une hauteur h = 1,8 m par rapport au sol : |
Son énergie cinétique initiale est égale à 9,0
x 10
– 2 J |
Sa vitesse est égale à 6,0 m / s lorsqu’elle touche le sol |
Son énergie potentielle de pesanteur a augmenté de 9,0
x 10
– 2 J
|
B |
►
Différentes formes d’énergie :
-
Aux diverses interactions
fondamentales, on peut associer des formes d’énergie.
|
Interaction fondamentale |
Énergie associée |
|
Interaction
gravitationnelle |
Énergie potentielle de
pesanteur |
|
interaction
électromagnétique |
Énergie électrique,
énergie chimique, … |
|
Interaction forte ou
faible |
Énergie nucléaire |
-
Tout ce qui vie fonctionne,
évolue, nécessite de l'énergie.
-
L’énergie électrique est associée
à l’interaction électromagnétique.
-
L’énergie nucléaire est associée
à l’interaction forte
ou faible.
►
Énergie cinétique :
- L’énergie cinétique EC est l’énergie que possède un solide du fait de son mouvement.
- Elle dépend de la vitesse et de la masse du solide.
- Pour un solide animé d’un mouvement de translation, tous les points du solide ont à chaque instant la même vitesse que le centre d’inertie :
- L’énergie cinétique EC d’un solide en mouvement de translation est égale au demi-produit de la masse m du solide par le carré de la vitesse vG2 du centre d’inertie du solide.
- On écrit :

- L’énergie cinétique caractérise un solide en mouvement.
- Elle est :
- Proportionnelle à la masse m du solide
- Proportionnelle au carré de la vitesse du solide.
- Elle dépend du référentiel d’étude.
►
Vitesse et énergie cinétique :
-
Relation :

►
Énergie potentielle de
pesanteur :
-
L’énergie potentielle de pesanteur d’un solide est
l’énergie qu’il possède du fait de son interaction avec la Terre.
-
La valeur de cette
énergie dépend de la position du solide par rapport à la Terre.
- Expression :

- Remarque 1 : La valeur de l’énergie potentielle de pesanteur dépend de la valeur de z, elle dépend du choix de l’origine des altitudes. L’énergie potentielle est définie à une constante additive près.
- Si l’on choisit comme origine des énergies potentielle le sol : Ep (0) = 0
- Ep = m . g . z = m . g . h
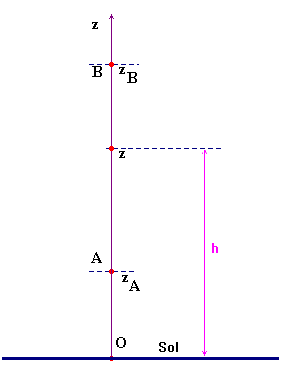
- La différence d’énergie potentielle ne dépend pas du choix de l’origine.
- Pour les exercices, on choisit l’origine la plus commode, celle qui simplifie les calculs.
►
Énergie mécanique d’un solide.
- L’énergie mécanique d’un solide est la somme de son énergie cinétique et de son énergie potentielle.
-
Relation : Em
= EC +
EP.
►
Balle lancée dans un champ de
pesanteur uniforme :
-
Au cours du mouvement de la
balle :
-
L’énergie potentielle de
pesanteur augmente, passe par une valeur maximale puis diminue.
-
Alors que l’énergie cinétique
diminue, passe par une valeur minimale puis augmente.
-
Quand l’énergie cinétique
diminue, l’énergie potentielle augmente et inversement.
-
Il y a transformation mutuelle
d’énergie potentielle de pesanteur en énergie cinétique.
-
L’énergie mécanique garde une
valeur pratiquement constante, on peut dire qu’elle se conserve.
-
L’étude énergétique de ce
mouvement montre que :
-
Les forces de frottement sont
négligeables et que
- La balle est en chute libre.
►
Chute libre :
-
On appelle chute libre le mouvement d'un objet soumis
uniquement à son poids
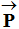 .
.
- Une balle de masse m tombe en chute libre d’une hauteur h.
- Si la balle est en chute libre sans vitesse initiale, on trouve la relation suivante :
- v2 = 2 g . h
►
Système isolé :
-
Un système est isolé si aucun
transfert d'énergie n'est possible entre le système et le milieu
extérieur.
-
L’énergie d’un système isolé ne
peut être ni détruite, ni créée.
-
L'énergie d'un système isolé se
conserve, elle est constante.
-
Un système isolé n’effectue aucun
échange avec le milieu extérieur.
►
Transfert thermique :
-
Lorsqu’un corps chaud et un corps
froid, isolés du milieu extérieur, sont en contact l’un avec
l’autre, il y a transfert thermique spontané du corps chaud vers
le corps froid.
-
Ce transfert s’accompagne de
variation de température ou de changement d’état.
-
Dans le cas d’un système isolé,
le gain d’énergie de la partie froide du système est égal à la
perte d’énergie de la partie froide du système.
-
Un transfert thermique s’effectue
spontanément du corps chaud vers le corps plus froid.
►
Calcul de l’énergie
cinétique d’une luge:
-


►
Calcul de l’énergie potentielle
de pesanteur :
-


►
Énergie cinétique multipliée par
quatre :
-
Pour que l’énergie cinétique d’un
solide soit multipliée par 4, il faut que la vitesse soit
multipliée par 2.
-
Dans l’expression de l’énergie
cinétique, la vitesse intervient au carré.
-
Expression :
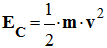
►
Objets ponctuels
A et B :
-
On donne : vA = 2 vB
et mB = 4 mA
-
Énergie cinétique de l’objet
ponctuel A :
-
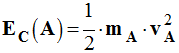
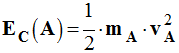
-
Énergie cinétique de l’objet
ponctuel B :
-
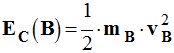
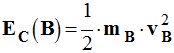
-
On en déduit :
-
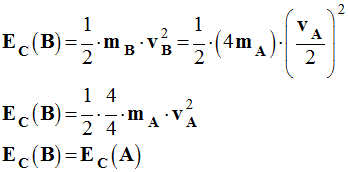
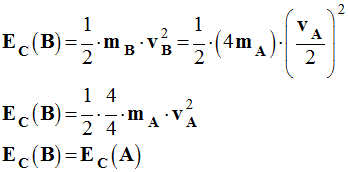
-
Énergie potentielle de pesanteur
-
Les deux objets sont à la même
altitude : zA = zB
-
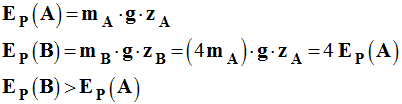
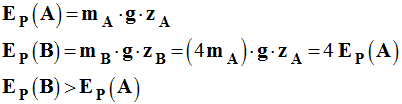
-
En conséquence :
-
EM
(B) > EM (A)
►
Bille en chute libre :
-
Instant initial :

-
Au niveau du sol :
-
À l’instant initial, l’énergie
cinétique de la bille est nulle car sa vitesse est nulle.
-
Sa vitesse est égale à 6,0 m / s
lorsqu’elle touche le sol
-
Son énergie mécanique se conserve.
-
On peut utiliser la loi de la chute
libre :
- v2 = 2 g . h
|
|