Pour aller plus loin : 

I- Notion de travail d’une force.

1)- Les effets d’une force.

- Une force appliquée à un solide peut avoir plusieurs effets :

- Une force peut mettre en mouvement un solide

- Une force peut modifier le mouvement d’un solide

-  Une force peut maintenir en équilibre un solide

- Une force peut déformer un solide.

- La question que l’on peut se poser : la force considérée produit-elle un travail mécanique ?

2)- Dans quel cas une force travaille-t-elle ? 

- Dans la vie de tous les jours, on associe la notion de travail à la notion d’effort.

- Lorsque la force exercée sur un mobile a un effet sur la valeur de la vitesse du mobile, on dit qu’elle travaille.

- Une force travaille, si son point d’application se déplace dans une direction qui n’est pas perpendiculaire à celle de la force.

- Une force ne travaille pas si :

- Sa direction est perpendiculaire à la trajectoire de son point d’application.

- Son point d’application ne se déplace pas.

- Exemple 1 :

- Un mobile autoporteur est placé sur une table à digitaliser horizontale.

-  À l’instant t = 0 s, on lâche le mobile autoporteur.

- Il est entraîné dans son mouvement par la masse marquée qui est accrochée au fil.

- Faire le bilan des forces appliquées au mobile autoporteur. Quelles sont les forces qui travaillent ?

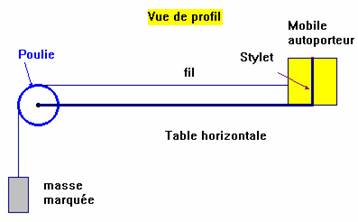
- Bilan des forces :

- Seule la force  travaille. 

- Les autres forces sont perpendiculaires à la direction de déplacement du point d’application de la force.

- Exemple 2 :

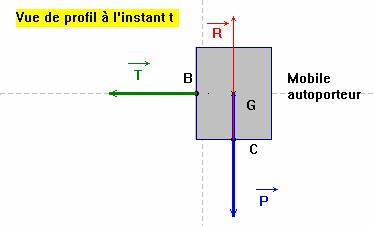
-  Le mobile autoporteur, maintenu par un fil tendu, est lancé sur la table à digitaliser.

-  La table est horizontale.

- Bilan des forces :

- Aucune force ne travaille : 

- Les forces sont perpendiculaires à la direction de déplacement du point d’application de la force.

- Conclusion :

- Une force dont le point d’application se déplace peut mettre en mouvement un objet.

- Elle peut modifier sa vitesse, son altitude, sa température ou le déformer. On dit que la force travaille.

- De plus, le travail d’une force peut être moteur ou résistant.

II- Travail d’une force constante.

1)- La force constante.

- Exemple : le poids d’un objet peut constituer une force constante dans certaines conditions.

- Une force est constante si sa valeur, sa direction et son sens ne varient pas au cours du temps.

2)- Définition du travail.

- Schéma :

- Calculer le travail de la force  sachant que : F = 10 N, ℓ = 7,70 cm et α = 30 °.

- 

- Calculer le travail de la même force  sur le trajet AC puis sur le trajet CB. Comparer les résultats obtenus et conclure.

- Déplacement AC :

- 

- Déplacement CB :

- 

- On remarque que :

- 

- Le travail d’une force constante, lors du déplacement de son point d’application entre A et B ne dépend pas du chemin suivi entre A et B.

- On est en présence d’une force conservative.

3)- Travail moteur et travail résistant.

- Le travail est une grandeur algébrique.

- 

III- Le travail du poids d’un corps.

1)- Hypothèse.

- Sur une zone étendue à quelques kilomètres, on peut considérer le vecteur poids est une force constante.

- La valeur du poids P = m.g.

-  La grandeur g dépend de l’altitude et de la latitude.

- Pour un déplacement de quelques kilomètres on peut considérer que g = c^te.

- Exemple : Solide sur un plan incliné.

- Considérons un mobile autoporteur de masse m = 400 g se déplaçant sur un plan incliné d’un angle β = 26,2 ° par rapport à l’horizontale.

- Que peut-on dire du travail de la force , réaction du support sur le même trajet AB ?

-  Donner l’expression du travail du poids  sur le trajet AB.

-  Utiliser le fait que le vecteur  est une force constante.

- En déduire l’expression du travail du poids  sur le trajet AB en fonction de la dénivellation h entre les positions A et B du mobile.

- Le travail du poids  sur le trajet AB est-il moteur ou résistant ?

- On choisit un axe vertical Oz, orienté vers le haut et d’origine O.

- Lorsque le mobile occupe la position A, il a l’altitude z_A et lorsqu'il occupe la position B, il a l’altitude z_B.

- Exprimer le travail du poids sur le trajet AB en fonction de z_A et z_B. Conclusion.

- Calculer la valeur du travail du poids  sur le trajet AB sachant que AB = 10,0 m .

2)- Calcul du travail du poids.

- Le travail de la force , réaction du support, sur le même trajet AB est nul car la réaction du support est perpendiculaire au support. 

- Les frottements sont négligeables.

-  Expression du travail du poids  sur le trajet AB.

- 

- On va utiliser deux propriétés du poids : la direction du poids est la verticale du lieu et la valeur du poids est constante. 

- Le poids est une force constante.

-  Le travail du poids ne dépend pas du chemin suivi.

- On choisit le chemin suivant : AH et HB.

- 

- Le travail du poids  sur le trajet AB est un travail moteur :

- 

- Pour donner le travail du poids en fonction de z_A et z_B, il faut donner l’expression des vecteurs  et  en utilisant l’axe Oz et le vecteur unitaire .

- On peut écrire que :

-   (1)

-   (2)

- En conséquence : 

- 

- Valeur du travail du poids :

- 

IV- Puissance d’une force.

1)- Introduction.

- La puissance mécanique d’une force est liée à la rapidité avec laquelle un travail donné W peut être effectué.

- Exemple : une grue de chantier soulève à vitesse constante, un container de masse m = 5,0 t,

  d’une hauteur h = 13 m , en une durée de 24 s.

- Cette grue développe une certaine puissance.

- Comme un cycliste au moment d’un sprint développe une certaine puissance. 

- C’est le plus puissant qui effectue le travail le plus rapidement et dans le cas d’un sprint arrive le premier.

-  La grandeur puissance, relie la notion de travail à la notion de durée.

2)- Puissance moyenne.

- Par définition : la puissance moyenne d’une force  sur le trajet AB est égale

- Au quotient du travail  par la durée Δt du déplacement.

-  L’unité légale de puissance est le watt symbole W.

- Calculer la puissance développée par la grue.

- La réciproque du principe de l’inertie permet de dire que : F = P car le mouvement est rectiligne uniforme.

- Le travail de la fore est moteur, c’est l’opposé du travail du poids :

- Puissance développée par la grue :

- 

- Quelques valeurs de puissance :

3)- Puissance instantanée.

La puissance instantanée P (t) d’une force  sur le trajet AB,

 est évaluée en considérant le petit travail W effectué

pendant une courte durée Δt encadrant la date considérée t.

-  On peut écrire que :

- 

- On peut assimiler le rapport  au vecteur vitesse instantanée

- 

- La puissance instantanée peut s’écrire :

- Avec : P en watt (W), F en newton (N) et v en mètre par seconde (m / s).

- Application :

- Déterminer la valeur de la vitesse de déplacement du container

- En déduire la valeur de la puissance instantanée développée par la grue.

- Valeur de la vitesse de déplacement du container :

- 

- Puissance instantanée développée par la grue :

- 

V- Applications.

1)- QCM :

2)- Exercices :