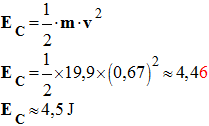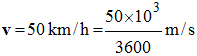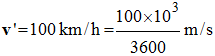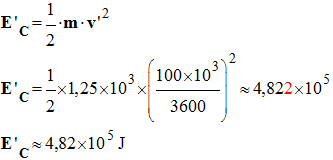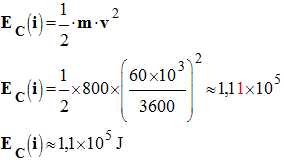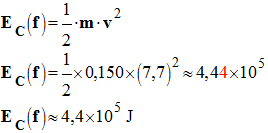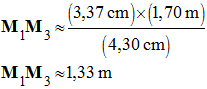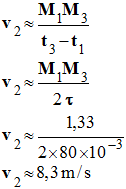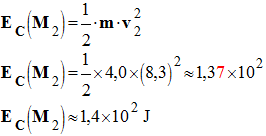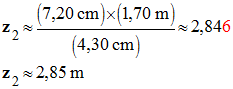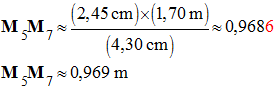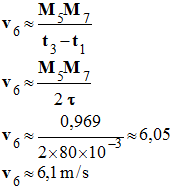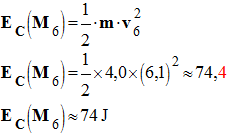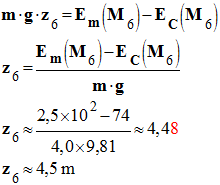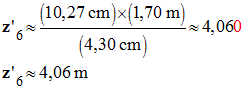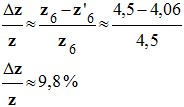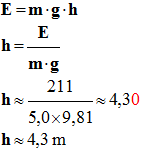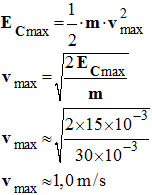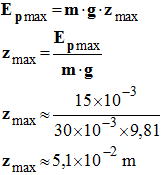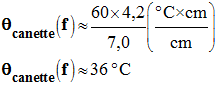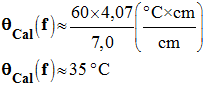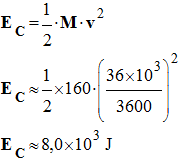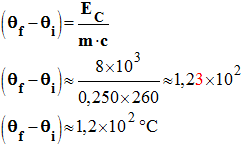Chap N° 08 de Physique : Principe de conservation de l'énergie, exercices de sciences physiques première S 2011

Phys. N° 08

Principe de conservation de l'énergie.

Exercices.

Mots clès :
Principe de conservation de l'énergie, énergie,
énergie liée à la vitesse, énergie cinétique, énergie liée à la position,

énergie potentielle, énergie liée à l'altitude,
Exploitation du principe de conservation de l'énergie,
cas de la chute libre, chute libre, chute avec frottements, vitesse limite,
transfert thermique,
la radioactivité béta moins, le neutrino, l'antineutrino,
Fermi, Pauli,
freinage d'une voiture, chute d'une pomme, lancer du poids,

expérience de Joule, pendule simple et énergie, freiner en scooter, transferts thermiques, ...

I- Exercice 6 page 229. Connaître l’énergie cinétique.

II- Exercice 7 page 229. Calculer une énergie cinétique.

III- Exercice 8 page 229. Connaître l’énergie potentielle.

IV- Exercice 9 page 229. Calculer une énergie potentielle de pesanteur.

V- Exercice 11 page 230. Étudier le freinage d’une voiture.

VI- Exercice 15 page 230. Chute de la pomme.

VII- Exercice 20 page 232. Le lancer du poids.

VIII- Exercice 20 page 232. Expérience de Joule.

IX- Exercice 22 page 233. Pendule simple et énergie.

X- Exercice 24 page 233 Transferts thermiques.

XI- Exercice 26 page 235. Freiner en scooter.

Transferts d'énergie et conservation

Transferts d'énergie et énergie interne. Cours.

Etude de la chute libre.

Travail d'une force

Energie cinétique

I- Exercice 6 page 229. Connaître l’énergie cinétique.

1)- Quelle est l’expression littérale de l’énergie cinétique pour un solide en translation ?

Préciser la signification des termes et des unités.

2)- Calculer l’énergie cinétique d’une pierre de curling de masse m = 19,9 kg

se déplaçant avec une vitesse v de valeur v = 0,67 m / s.

1)- Expression littérale de l’énergie cinétique pour un solide en translation :

► Définition :

- L’énergie cinétique E_C d’un solide en mouvement de translation est égale

au demi-produit de la masse m du solide par le carré de la vitesse v² du solide.

- On écrit :

- Unités :

E_C : énergie cinétique d’un solide en mouvement de translation en joule (J)

m : masse du solide en kilogramme (kg)

v : vitesse du solide en mètre / seconde (m / s)

- L’énergie cinétique caractérise un solide en mouvement par rapport à un référentiel.

2)- Valeur de l’énergie cinétique d’une pierre de curling :

- Valeur de la masse m = 19,9 kg

- Valeur de la vitesse v = 0,67 m / s.

II- Exercice 7 page 229. Calculer une énergie cinétique.

1)- Calculer l’énergie cinétique d’une voiture de masse m = 1,25 t roulant à la vitesse v = 50 km / h.

2)- Calculer cette énergie si elle roule à la vitesse v’ = 100 km / h.

1)- Valeur de l’énergie cinétique de la voiture pour la vitesse v :

- Valeur de la masse m = 1,25 t = 1,25 × 10 ³ kg

- Valeur de la vitesse :

- Valeur de l’énergie cinétique :

2)- Valeur de l’énergie cinétique de la voiture pour la vitesse v’ :

- Valeur de la masse m = 1,25 t = 1,25 × 10 ³ kg

- Valeur de la vitesse :

- Valeur de l’énergie cinétique :

- Remarque : v’ = 2 v

- En conséquence, E’_C = 4 E_C.

- Pour un objet de masse m, lorsque la vitesse double, son énergie cinétique est multipliée par 4.

III- Exercice 8 page 229. Connaître l’énergie potentielle.

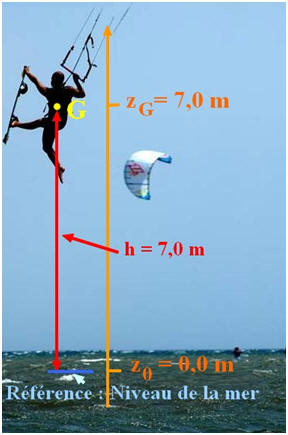
1)- Énergie potentielle :

a)- Quelle est l’expression de l’énergie potentielle de pesanteur ?

b)- Préciser la signification des termes, leur unité et les conditions d’application de l’expression.

2)- Lors d’une figure de freestyle, une kitesurfeuse de masse m = 50 kg réussit à s’élever à 7,0 m au-dessus de la mer.

En prenant le niveau de la mer comme référence des énergies potentielles,

calculer son énergie potentielle de pesanteur au point le plus haut de son saut.

1)- Énergie potentielle :

a)- Expression de l’énergie potentielle de pesanteur :

- L’énergie potentielle de pesanteur E_p d’un solide est l’énergie qu’il possède du fait de sa position par rapport à la Terre, c’est-à-dire du fait de son altitude.

- Un solide de masse m est soumis à son poids sur la Terre.

- L’énergie potentielle de pesanteur E_p d’un solide est l’énergie qu’il possède du fait de son interaction avec la Terre.

- La valeur de cette énergie dépend de la position du solide par rapport à la Terre.

- Expression : E_p = m . g . z.

b)- Signification des termes, leur unité et les conditions d’application de l’expression :

- E_p = m . g . z.

E_p = m . g . z : Énergie potentielle de pesanteur en joule J

m : Masse de l’objet en kilogramme kg.

g : Facteur d’attraction terrestre : g = 9,81 N / kg ou g = 9,81 m / s².

z : Altitude du centre d’inertie de l’objet en mètre m.

- Remarque 1 : La valeur de l’énergie potentielle de pesanteur dépend de la valeur de z,

- elle dépend du choix de l’origine des altitudes.

- L’énergie potentielle est définie à une constante additive près.

- La différence d’énergie potentielle ne dépend pas du choix de l’origine.

- L’axe des altitudes est orienté vers le haut.

2)- Valeur de l’énergie potentielle de pesanteur au point le plus haut de son saut :

- Schéma :

- E_p (G) = m . g . z_G

- E_p (G) = 50 × 9,81 × 7,0

- E_p (G) ≈ 3,4 × 10³J

IV- Exercice 9 page 229. Calculer une énergie potentielle de pesanteur.

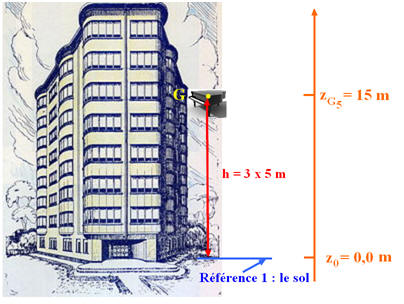
George vient d’acheter du café pour préparer sa boisson préférée.

À la sortie du magasin, un piano lui tombe sur la tête (What else !).

On considère que le piano a une masse m = 275 kg et qu’il tombe du cinquième étage, chaque étage ayant une hauteur h = 3,0 m.

1)- Calculer l’énergie potentielle de pesanteur du piano juste avant qu’il ne tombe.

2)- Calculer la variation de l’énergie potentielle de pesanteur lorsqu’il passe du cinquième au deuxième étage.

Commenter le signe de la valeur obtenue.

3)- Reprendre les questions 1 et 2 en choisissant comme nouvelle origine des énergies potentielles de pesanteur le niveau du cinquième étage.

1)- Valeur de l’énergie potentielle de pesanteur du piano juste avant qu’il ne tombe :

- Schéma :

- Valeur de l’énergie potentielle de pesanteur du piano juste avant qu’il ne tombe :

- E_p (G₅) = m . g . z_G5

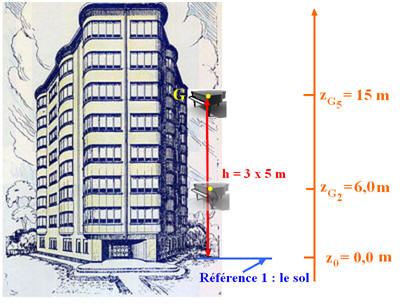
- E_p (G₅) = 275 × 9,81 × 15

- E_p (G₅) ≈ 4,8 × 10⁴J

2)- Valeur de la variation de l’énergie potentielle de pesanteur lorsqu’il passe du cinquième au deuxième étage :

- Schéma :

- ΔE_p = m . g . z_G2 – m . g . z_G5

- ΔE_p = m . g . (z_G2 – z_G5)

- ΔE_p = 275 × 9,81 × (6,0 – 15)

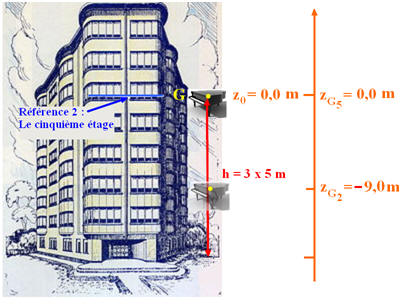
- ΔE_p ≈ – 2,4 × 10⁴J

3)- Choix d’une nouvelle origine :

a)- Valeur de l’énergie potentielle de pesanteur du piano juste avant qu’il ne tombe :

- E_p (G₅) = m . g . z_G5

- E_p (G₅) = 275 × 9,81 × 0,0

- E_p (G₅) ≈ 0,0J

b)- Valeur de la variation de l’énergie potentielle de pesanteur lorsqu’il passe du cinquième au deuxième étage :

- ΔE_p = m . g . z_G2 – m . g . z_G5

- ΔE_p = m . g . (z_G2 – z_G5)

- ΔE_p = 275 × 9,81 × (– 9 ,0 – 0,0)

- ΔE_p ≈ – 2,4 × 10⁴J

► Remarque 1 :

- La valeur de l’énergie potentielle de pesanteur dépend de la valeur de z, elle dépend du choix de l’origine des altitudes.

► Remarque 2 :

- La valeur de la variation de l’énergie potentielle de pesanteur est indépendante de l’origine des altitudes choisie.

V- Exercice 11 page 230. Étudier le freinage d’une voiture.

Une voiture de masse m = 800 kg roule à la vitesse v = 60 km / h sur une route horizontale.

Le conducteur freine et la voiture s’arrête.

1)- Quelle est l’énergie cinétique initiale de la voiture ?

2)- Quelle est l’énergie perdue par la voiture lors de son arrêt ? Comment est dissipée cette énergie ?

1)- Énergie cinétique initiale de la voiture :

2)- Énergie perdue par la voiture lors de son arrêt :

- Après freinage, la voiture s’arrête et l’énergie cinétique de la voiture s’annule.

- Comme la voiture roule sur une route horizontale, son énergie potentielle de pesanteur ne varie pas.

- Seule son énergie cinétique varie.

- L’énergie perdue par la voiture est égale à l’énergie cinétique initiale de la voiture :

- E_perdue = E_C (i) ≈ 1,1 × 10⁵ J

- Cette énergie est dissipée par transfert thermique.

VI- Exercice 15 page 230. Chute de la pomme.

Une pomme de masse m = 150 g, accrochée dans un pommier, se trouve à une hauteur h = 3,0 m au-dessus du sol.
Le sol est choisi comme référence des énergies potentielles de pesanteur.
1)- Lorsque la pomme est accrochée dans le pommier, quelle est :
a)- Son énergie cinétique ?
b)- Son énergie potentielle de pesanteur ?
c)- Son énergie mécanique ?
2)- La pomme se détache et arrive au sol avec une vitesse v = 7,7 m / s.
Calculer son énergie cinétique, son énergie potentielle de pesanteur et son énergie mécanique lorsqu’elle arrive au sol.
3)- Quelles transformations énergétiques ont eu lieu au cours de cette chute ?
4)- Quelle serait la hauteur de chute de cette même pomme si elle arrivait au sol avec une vitesse v’ = 9,9 m / s.

1)- La pomme est accrochée dans le pommier : état initial i.

a)- Énergie cinétique de la pomme :

- La pomme est immobile, son énergie cinétique est nulle dans le référentiel lié au sol.

- E_C (i) = 0,0 J

b)- Énergie potentielle de la pomme :

- E_p (i) = m . g . z_i

- E_p (i) = 0,150 × 9,81 × 3,0

- E_p (i) ≈ 4,4 J

c)- Énergie mécanique de la pomme :

- E_m (i) = E_C (i) + E_p (i) = E_p (i)

- E_m (i) ≈ 4,4 J

2)- La pomme arrive au sol : état final f.

- Énergie cinétique de la pomme :

- Énergie potentielle de pesanteur de la pomme lorsqu’elle arrive au sol :

- E_p (f) = m . g . z_f

- E_p (i) = 0,150 × 9,81 × 0,0

- E_p (i) ≈ 0,0 J

- Énergie mécanique de la pomme lorsqu’elle arrive au sol :

- E_m (f) = E_C (f) + E_p (f) = E_p (f)

- E_m (f) ≈ 4,4J

3)- Transformations énergétiques :

- On remarque que : E_m (i) = E_m (f) ≈ 4,4 J

- Au cours de la chute, l’énergie mécanique de la pomme se conserve.

- Au cours de la chute l’énergie potentielle de pesanteur a été convertie en énergie cinétique.

4)- Hauteur h’ de chute de cette pomme.

- L’énergie potentielle de pesanteur a été convertie en énergie cinétique :

- On peut écrire :

- État initial :

- E_C (i) = 0,0 J et E_p (i) = m . g . z

- E_m (i) = E_C (i) + E_p (i) = E_p (i) = m . g . z

- État final :

- E_C (f) = ½ m . v’² et E_p (i) = 0,0 J

- E_m (f) = E_C (f) + E_p (f) = E_C (f) = ½ m . v’²

- Au cours de la chute, l’énergie mécanique de la pomme se conserve.

- E_m (i) = E_m (f)

- m . g . z = ½ m . v’²

VII- Exercice 20 page 232. Le lancer du poids.

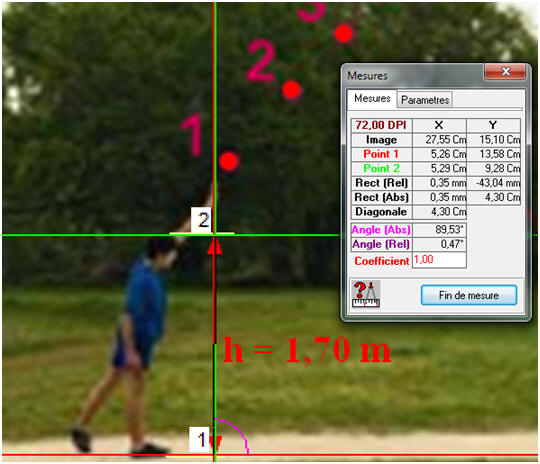
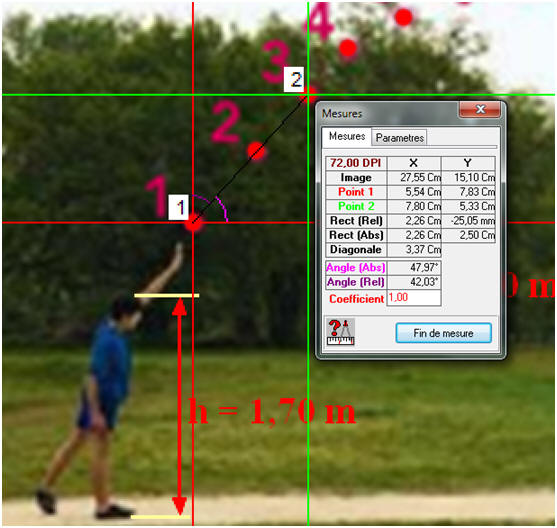
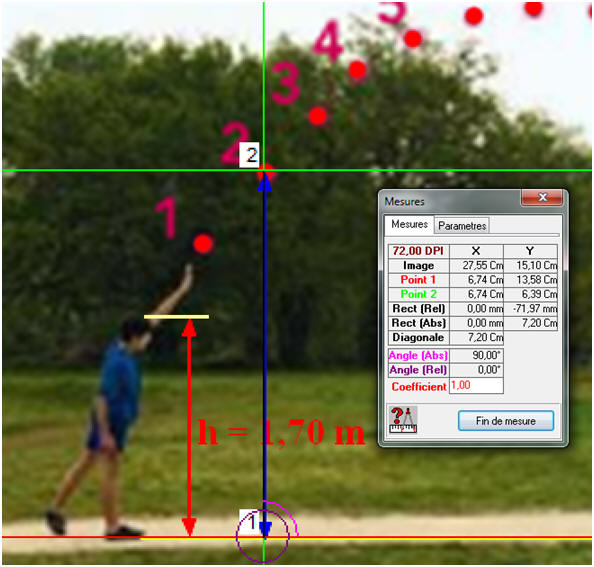
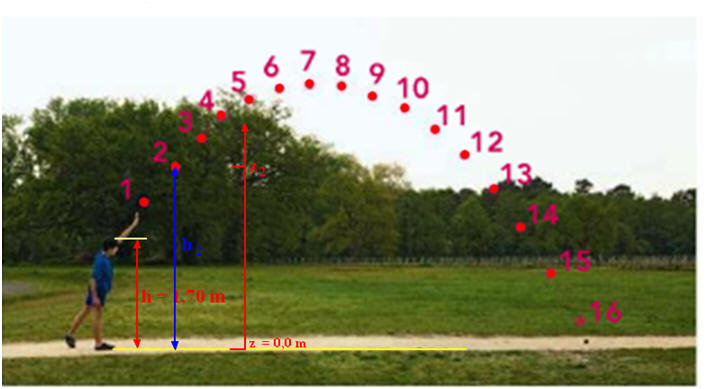
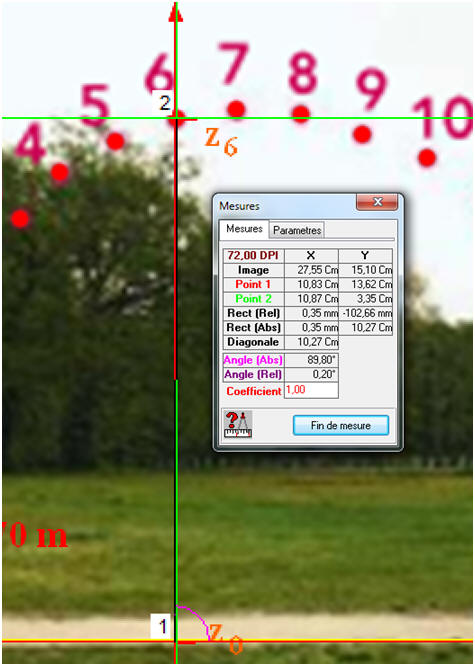
Un lycéen mesurant h = 1,70 m effectue un lancer de « poids » de masse m = 4,0 kg.

On prendra la référence des énergies potentielles de pesanteur au niveau du sol.

L’étude d’une vidéo de ce lancer a permis d’obtenir le relevé des positions ci-dessous.

L’intervalle de temps entre deux positions consécutives vaut τ = 80 ms.

1)- Énergie cinétique :

a)- En mesurant la distance parcourue par le « poids » entre les points 1 et 3,

calculer la valeur de la vitesse v₂ du poids lorsqu’il arrive au point 2.

b)- En déduire l’énergie cinétique du « poids » au point 2.

2)- Énergie potentielle et énergie mécanique :

a)- Calculer l’énergie potentielle de pesanteur du « poids » lorsqu’il se situe au point 2.

b)- En déduire son énergie mécanique au point 2.

3)- Calculer l’énergie cinétique du « poids » au point 6 à partir d’une étude analogue à celle de la question 1.

4)- Énergie mécanique :

a)- Si l’on considère que l’énergie mécanique se conserve, quelle devrait être l’altitude atteinte par le « poids » au point 6 ?

b)- Comparer le résultat précédent à la mesure réalisée sur l’image.

Que penser de l’hypothèse sur la conservation de l’énergie mécanique ?

Les mesures ont été effectuées avec le logiciel PHOTOPHILTRE et le Plugins "Mesures" Mode d'emploi

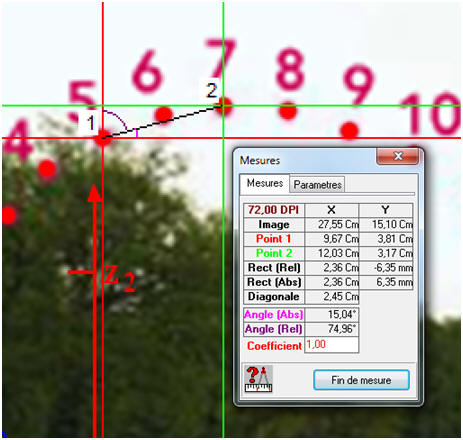
1)- Énergie cinétique :

a)- Valeur de la vitesse v₂ du poids lorsqu’il arrive au point 2 :

- Référence des mesures :

- Mesures pour la vitesse :

- Distance parcourue :

	Distance du point M₁ au point M₃	Taille lycéen
Réalité	M₁M₃	1,70 m
Image	3,37 cm	4,30 cm

- La vitesse à l’instant t₂ est pratiquement égale à la vitesse moyenne calculée

pendant un intervalle de temps très court encadrant l’instant t₂ considéré.

b)- Énergie cinétique du « poids » au point 2.

2)- Énergie potentielle et énergie mécanique :

a)- Énergie potentielle de pesanteur du « poids » lorsqu’il se situe au point 2.

- Altitude du point 2 :

	Altitude du point M₂	Taille lycéen
Réalité	z₂	1,70 m
Image	7,20 cm	4,30 cm

- E_p (M₂) = m . g . z₂

- E_p (M₂) = 4,0 × 9,81 × 2,85

- E_p (M₂) ≈ 1,1 × 10²J

b)- Énergie mécanique au point 2.

- E_m (M₂) = E_C (M₂) + E_p (M₂) ≈ 1,4 × 10² J + 1,1 × 10² J

- E_m (M₂) ≈ 2,5x 10² J

3)- Énergie mécanique :

a)- Altitude atteinte par le « poids » au point 6 :

- Vitesse du point au point 6 :

- Tableau de proportionnalité :

	Distance du point M₅ au point M₇	Taille lycéen
Réalité	M₅M₇	1,70 m
Image	2,45 cm	4,30 cm

- Distance parcourue par le poids :

- Vitesse du poids au point 6 :

- Énergie cinétique au point 6 :

4)- Comparaison :

- En considérant que l’énergie mécanique se conserve :

- E_m (M₂) = E_m (M₆) ≈ 2,5x 10² J

- E_m (M₆) = E_C (M₆) + E_p (M₆)

- E_p (M₆) = E_m (M₆) – E_C (M₆)

- Avec : E_p (M₆) = m . g . z₆

- Altitude du point M₆ :

- Si l’énergie mécanique se conserve, le poids doit atteindre l’altitude de 4,5 m au point 6.

- On peut vérifier à l’aide de l’image :

- Altitude z₆ dans ce cas :

	Altitude du point M₆	Taille lycéen
Réalité	z’₆	1,70 m
Image	10,27 cm	4,30 cm

- Écart entre les deux valeurs :

- On ne peut pas conclure que l’énergie mécanique se conserve.

- Il faudrait effectuer le calcul sur l’ensemble des mesures pour pouvoir faire une étude statistique.

- On peut se poser des questions sur la précision des mesures.

VIII- Exercice 21 page 232. Expérience de Joule.

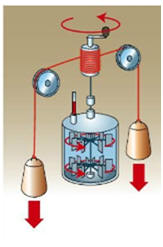
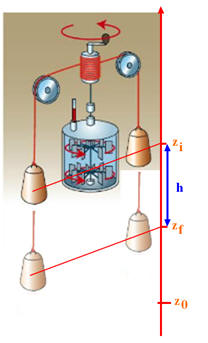
Au XIX siècle, le physicien britannique James Prescott Joule (1818 – 1889) a étudié des transformations entre diverses formes d’énergie.

L’unité d’énergie du système international porte son nom.

Pour reproduire son expérience au laboratoire, on dispose d’une enceinte isolée thermiquement du milieu extérieur.

Une telle enceinte est appelée calorimètre.

Il contient de l’eau à la température initiale de θ_i =15 ° C.

Deux masses, de 5,0 kg au total, reliées à deux poulies, permettent de faire tourner dans l’eau un système de pales.

Ces masses descendent d’une hauteur h.

La température de l’eau augmente de 1,0 ° C sous l’action de la rotation des pales.

1)- Quelle forme d’énergie possèdent les masses avant leur chute ?

2)- Quelle est la conversion d’énergie qui s’opère dans le calorimètre ?

3)- En utilisant le principe de conservation de l’énergie et en négligeant les forces de frottement à l’extérieur du calorimètre,

que peut-on dire de l’énergie reçue par le système {eau + calorimètre} par rapport à celle perdue par les masses ?

4)- L’énergie reçue par le système {eau + calorimètre} vaut 211 J. Calculer la hauteur de chute h des masses.

1)- Forme d’énergie possèdent les masses avant leur chute :

- Avant leur chute, les masses ne possèdent pas d’énergie cinétique car elles sont immobiles.

- Elles possèdent de l’énergie potentielle de pesanteur par rapport au sol.

2)- Conversion d’énergie dans le calorimètre :

- Au cours de l’évolution du système, {masses + eau + calorimètre},

les masses descendent d’une hauteur h et la température de l’eau augmente de 1° C.

- Il y a conversion d’énergie mécanique (ici énergie cinétique) en énergie thermique.

3)- Conservation de l’énergie :

- L’énergie du système {masses + eau + calorimètre} se conserve.

- L’énergie reçue par le système {eau + calorimètre} est égale à l’énergie perdue par les masses.

4)- Hauteur de chute h des masses :

- État initial : E_C (i) = 0,0 J et E_p (i) = m . g . z_i

- État initial : E_C (f) = 0,0 J et E_p (f) = m . g . z_f

- Variation de l’énergie mécanique ;

- ΔE_m = Δ E_C + Δ E_p = [E_C (f) – E_C (i)] + [E_p (f) – E_p (i)]

- ΔE_m = m . g . z_f – m . g . z_i

- ΔE_m = – m . g . (z_i – z_f)

- ΔE_m = – m . g . h

- Énergie mécanique du système constituée par les masses a diminué.

- En utilisant le principe de conservation de l’énergie pour :

- le système {masses + eau + calorimètre},

- le système {eau + calorimètre} gagne l’énergie E, telle que :

- ΔE_m + E = 0

- E = m . g . h

IX- Exercice 22 page 233. Pendule simple et énergie.

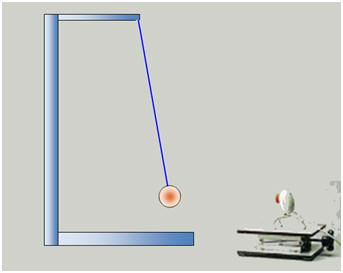
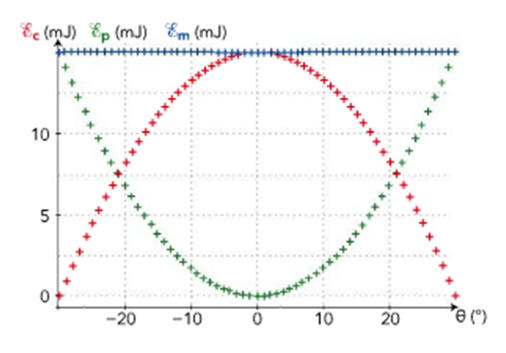
Le mouvement d’un pendule simple a été filmé.

Le traitement avec un logiciel de pointage vidéo a permis d’obtenir les courbes ci-après.

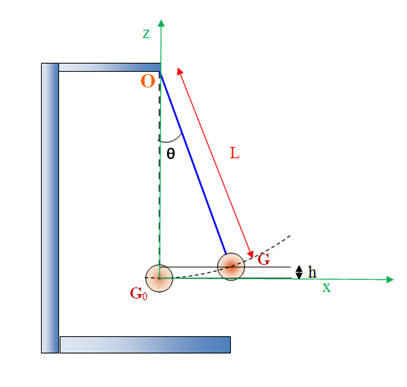
Ce pendule est constitué d’une bille de masse m = 30 g suspendue à l’extrémité

d’un fil inextensible de masse négligeable (devant celle de la bille).

L’autre extrémité du fil est accrochée en un point O fixe dans le référentiel terrestre.

Le repère (G₀, x, z) est orienté comme sur la figure ci-dessus.

L’altitude de G₀ est prise pour référence des énergies potentielles de pesanteur.

1)- Rappeler l’expression de l’énergie cinétique du pendule. Expliciter chaque terme et préciser l’unité.

2)- Énergie potentielle de pesanteur :

a)- Rappeler l’expression de l’énergie potentielle de pesanteur du pendule en fonction de z.

Préciser les unités.

b)- Pour quelle valeur de l’angle θ l’énergie potentielle de pesanteur du pendule est-elle nulle ?

3)- D’après les courbes, comment varie l’énergie mécanique du système ?

Que peut-on en conclure sur les forces de frottement de l’air exercées sur la bille ?

4)- Expliquer brièvement ce qui se passe du point de vue énergétique lors d’une oscillation.

5)- Énergies :

a)- Quelle est l’énergie cinétique maximale du pendule ?

b)- En déduire la valeur de la vitesse maximale du pendule.

c)- Calculer la hauteur maximale atteinte par le pendule.

1)- Expression de l’énergie cinétique du pendule.

► Définition :

- L’énergie cinétique E_C d’un solide en mouvement de translation est égale

au demi-produit de la masse m du solide par le carré de la vitesse v² du solide.

- On écrit :

- Unités :

E_C : énergie cinétique d’un solide

en mouvement de translation en joule (J)

m : masse du solide en kilogramme (kg)

v : vitesse du solide en mètre / seconde (m / s)

- L’énergie cinétique caractérise un solide en mouvement par rapport à un référentiel.

2)- Énergie potentielle de pesanteur :

a)- Expression de l’énergie potentielle de pesanteur du pendule en fonction de z.

- L’énergie potentielle de pesanteur E_p d’un solide est l’énergie qu’il possède du fait de son interaction avec la Terre.

- La valeur de cette énergie dépend de la position du solide par rapport à la Terre.

- Expression : E_p = m . g . z.

- E_p = m . g . z.

E_p = m . g . z : Énergie potentielle de pesanteur en joule (J)

m : Masse de l’objet en kilogramme (kg).

g : Facteur d’attraction terrestre : g = 9,81 N / kg ou g = 9,81 m / s².

z : Altitude du centre d’inertie de l’objet en mètre (m).

- L’énergie potentielle est définie à une constante additive près.

b)- Valeur de l’angle θ :

- Avec la référence choisie, l’énergie potentielle de pesanteur est nulle lorsque θ = 0 °.

3)- Variation de l’énergie mécanique du système au cours d’une oscillation :

- On remarque qu’au cours d’une oscillation, l’énergie mécanique se conserve, elle garde la même valeur :

- E_m = cte ≈ 15 mJ (lecture graphique)

- Dans le cas présent, on peut négliger les forces de frottement.

- Les forces de frottement sont négligeables.

4)- Lors d’une oscillation :

- Pour θ = – 30 °, E_C (- 30) = 0,0 mJ et E_p (- 30) = 15 mJ

- Puis au cours de l’oscillation, l’énergie cinétique augmente et l’énergie potentielle de pesanteur diminue.

- Lorsque l’énergie cinétique est maximale, l’énergie potentielle de pesanteur est nulle (minimale).

- Puis l’énergie cinétique diminue et l’énergie potentielle de pesanteur augmente.

- Lorsque l’énergie potentielle de pesanteur est maximale, l’énergie cinétique est minimale (nulle).

- Au cours d’une oscillation, il y a conversion d’énergie potentielle de pesanteur en énergie cinétique et inversement.

- Il y a échange mutuel d’énergie potentielle de pesanteur en énergie cinétique de telle sorte que l’énergie mécanique du système se conserve.

- E_C (θ) + E_p (θ) = E_m = cte

5)- Énergies :

a)- Énergie cinétique maximale du pendule :

- Par lecture graphique : E_Cmax = E_C (0) ≈ 15 mJ

b)- Valeur de la vitesse maximale du pendule :

c)- Hauteur maximale atteinte par le pendule :

- Lorsque le pendule atteint la hauteur maximale z_max, son énergie potentielle de pesanteur est maximale :

- E_p_max = m . g . z_max ≈ 15 mJ

X- Exercice 24 page 233 Transferts thermiques.

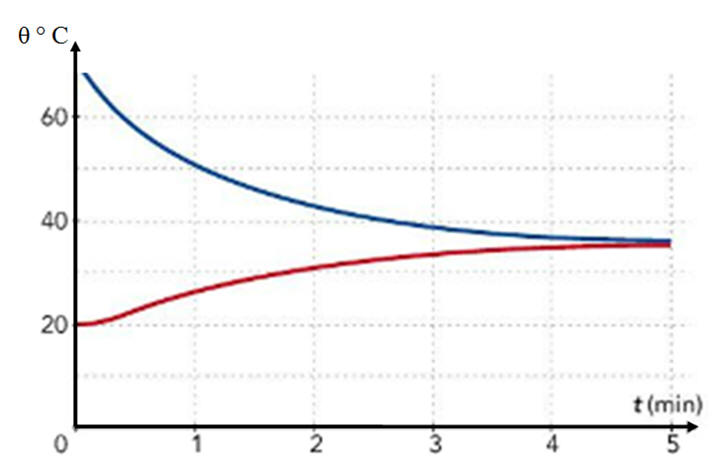
Dans un calorimètre contenant V₁ = 450 mL d’eau à θ₁ = 20 ° C, on introduit une petite canette contenant

V₂ = 200 mL d’eau à θ₂ = 70 ° C.

On place simultanément dans les deux liquides deux sondes de température reliées à un système d’acquisition.

Données : capacité thermique massique de l’eau : c_eau = 4,18 kJ / kg / °C

Masse volumique de l’eau : ρ_eau = 1000 kg / m³.

L’enregistrement des températures, durant cinq minutes, conduit aux courbes ci-dessus.

1)-

a)- Quelle a été la variation de température de l’eau de la canette durant les cinq minutes ?

b)- Quelle énergie a été cédée par l’eau de la canette ?

2)-

a)- Quelle a été la variation de température de l’eau du calorimètre ?

b)- Calculer l’énergie qui a été reçue par l’eau du calorimètre.

On donne la formule : E_th = m . c_eau . Δθ =

3)- Le calorimètre n’échange pas d’énergie avec le milieu extérieur.

Comment peut-on expliquer l’écart entre les valeurs précédentes ?

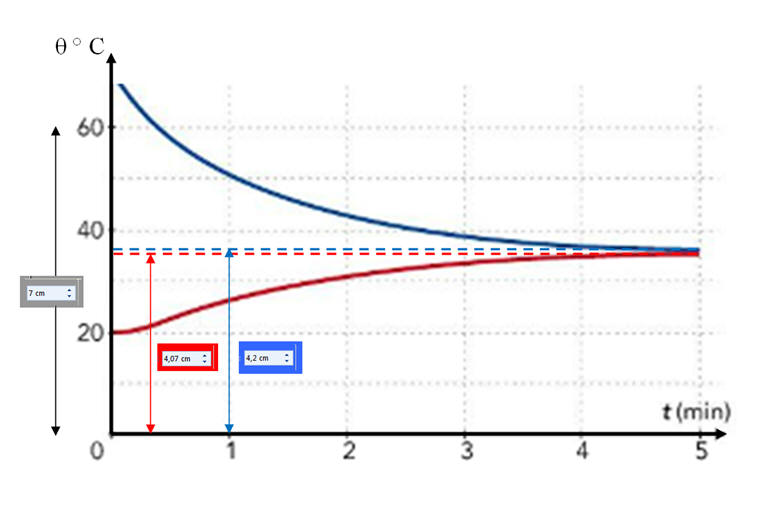
Les mesures ont été réalisées avec le logiciel Word (à l’aide de la longueur des flèches placées sur l’image des courbes)

1)-

a)- Variation de température de l’eau de la canette durant les cinq minutes :

- La température de l’eau de la canette diminue au cours du temps.

- Elle passe de 70 ° C à θ_canette (f).

Température	60 ° C	θ_canette (f)
Distance	7,0 cm	4,2 cm

- Variation de température de la canette :

- Δθ = θ_Cal (f) – θ_Cal (i) ≈ 36 ° C – 70 ° C

- Δθ ≈ – 34 ° C

b)- Énergie qui a été cédée par l’eau de la canette :

- L’eau de la canette cède de l’énergie thermique.

- On donne la formule : E_th = m . c_eau . Δθ.

- E_th = m₂ . c_eau . Δθ = ρ_eau . V₂. c_eau . Δθ.

- E_th ≈ 1000 x 200 x 10 ^{– 6} x 4,18 x (– 34) ≈ – 28,4

- E_th ≈ – 28 kJ

2)-

a)- Variation de température de l’eau du calorimètre :

- À l’instant initial, la valeur de la température du calorimètre est : θ_Cal (i) ≈ 20 ° C

- À l’équilibre thermique : θ_Cal (f)

Température	60 ° C	θ_Cal (f)
Distance	7,0 cm	4,2 cm

- Variation de température de l’eau du calorimètre :

- Δθ = θ_Cal (f) – θ_Cal (i) ≈ 35 ° C – 20 ° C

- Δθ ≈ 15 ° C

b)- Valeur de l’énergie qui a été reçue par l’eau du calorimètre.

- On donne la formule : E_th = m . c_eau . Δθ.

- E_th = m₁ . c_eau . Δθ = ρ_eau . V₁. c_eau . Δθ.

- E_th ≈ 1000 × 450 x 10 ^{– 6} × 4,18 × 15 ≈ 28,2

- E_th ≈ 28 kJ

3)- Écart entre les valeurs précédentes :

- Le système S = {calorimètre, eau calorimètre, canette, eau canette} est isolé.

- Le calorimètre est une enceinte adiabatique.

- L’énergie du système S se conserve.

- La source chaude (l’eau de la canette) cède de l’énergie à la source froide (eau du calorimètre)

afin d’obtenir l’équilibre thermique et une température d’équilibre θeq.

- Au bout de cinq minutes, le système a pratiquement atteint sa température d’équilibre.

- Avec la précision des mesures sur la température, on ne peut pas mettre en évidence de façon significative

d’écart entre les deux valeurs trouvées.

- Le calorimètre et ses accessoires possèdent une capacité calorifique qui est le plus souvent responsable

de l’écart observé lors d’une séance de travaux pratiques.

XI- Exercice 26 page 235. Freiner en scooter.

Greg roule à la vitesse v = 36 km / h, sur une route horizontale. Voyant un obstacle, il freine brutalement.

L’énergie cinétique du scooter et celle de Greg sont alors converties en énergie thermique qui provoque l’échauffement du système de freinage.

La masse totale du scooter additionnée à celle de Greg est M = 160 kg.

1)- Calculer, en joule, l’énergie cinétique totale E_C du système S = {Scooter + Greg} avant le freinage.

2)- Au cours du freinage, on admet que toute l’énergie cinétique se transforme intégralement en énergie thermique.

Le système de freinage de masse totale m = 250 g, possède une capacité thermique massique c = 260 J / kg / °C.

On donne l’énergie thermique reçue par les plaquettes : E_th = m . c . (θ_f – θ_i).

Calculer, en ° C, l’augmentation de température (θ_f – θ_i) des plaquettes.

3)- Indiquer si chaque affirmation ci-dessous est vraie ou fausse :

a)- Lors du freinage, l’énergie cinétique est conservée.

b)- Lors du freinage l’énergie cinétique est dissipée.

c)- L’énergie thermique du système de freinage double si la valeur de la vitesse double, toutes choses étant égales par ailleurs.

1)- Énergie cinétique totale E_C du système S = {Scooter + Greg} avant le freinage.

2)- Augmentation de température (θ_f – θ_i) des plaquettes.

- E_th = m . c . (θ_f – θ_i) = E_C.

3)- Vrai ou faux :

a)- Au cours du freinage, l’énergie cinétique diminue car la vitesse diminue.

- L’énergie cinétique n’est pas conservée : FAUX

b)- Au cours du freinage, l’énergie cinétique est dissipée : VRAI

c)- Par définition :

- Si on double la valeur de la vitesse, l’énergie thermique du système est multipliée par 4 car la vitesse intervient au carré :

- FAUX.

- (2v)² = 4 v²