I- L’intensité du courant électrique.

1)- Rappels et compléments.

a)-  Introduction.

-  Un courant électrique est un déplacement des porteurs de charge électrique, c’est un débit des porteurs de charge.

-  Dans un métal, le courant électrique est dû à un mouvement d’ensemble et ordonné des électrons libres.

-  Dans un électrolyte le courant électrique est dû à la double migration des ions positifs et négatifs qui se déplacent en sens inverses.

-  Par convention, le courant électrique sort de la borne positive du générateur.

b)-  Définition de l’intensité d’un courant électrique.

►  En régime permanent indépendant du temps :

-  L’intensité d’un courant électrique est le rapport de la quantité d’électricité Q ayant traversée une section s du circuit par la durée Δt.

-  C‘est un débit de charges électriques.

-  On écrit :

-  Plus le débit de charges électriques est élevé et plus l’intensité du courant est intense.

-  L’intensité du courant électrique se mesure à l’aide d’un ampèremètre placé en série dans la branche de circuit.

-  L’intensité, notée I s’exprime en ampère de symbole A.

►  En régime variable, dépendant du temps :

-  L’intensité du courant varie au cours du temps.

-  La définition précédente reste valable en faisant tendre la durée Δt vers zéro :

-  Δt → 0

-  Pendant la durée infiniment courte dt, une quantité d’électricité δq traverse une section s du circuit :

-  L’intensité i du courant est égale à la dérivée par rapport au temps de la charge transportée :

-  On écrit :

-   

►  En conclusion :

-  Quel que soit le régime de fonctionnement du circuit, l’intensité du courant électrique est un débit de charges électriques.

-  Pour une portion de conducteur électrique, l’intensité du courant i est la dérivée de la charge électrique par rapport au temps :

-   

►  Remarque :

-  L’intensité du courant correspond à la quantité de charges ayant traversé une section s d’un conducteur pendant la durée Δt.

-  Schéma :

-  À l’échelle microscopique, le déplacement des charges électriques est très lent.

-  À l’échelle macroscopique, la propagation du signal électrique est très rapide.

2)- La tension électrique : (rappel de seconde).

-  Représentation de la tension aux bornes d’un dipôle.

-  Schéma :

-  On représente la tension électrique par un segment fléché qui pointe vers la première lettre du symbole de cette tension.

-  L’unité de tension est le volt : V.

-  La tension est une grandeur algébrique.

-  Lors du branchement, il faut faire attention à l’ordre des bornes. 

-  U_AB = – U_BA

3)- Tension électrique et courant électrique.

-  En courant continu, l’intensité du courant est constante. On la note avec une lettre Majuscule I. Elle correspond à un débit de charges électriques.

-  De même une tension continue entre deux points A et B d’un circuit se note : U_AB

-  Les courants et les tensions sont qualifiés de variables si leurs valeurs varient au cours du temps.

-  On note ses grandeurs à l’aide de lettres minuscules : i pour l’intensité et u_AB pour la tension entre deux points A et B d’un circuit.

-  La loi d’additivité des tensions et la loi des nœuds sont vérifiées lorsque les circuits sont parcourus par des courants variables.

►  Le conducteur ohmique : Loi d’Ohm.

-  En courant continu et dans un circuit simple ne comportant qu’un générateur, le sens du courant est défini de la borne (+) vers la borne (–)

-  Par commodité, on oriente le dipôle en utilisant le sens du courant dans le circuit :

-  On peut écrire la loi d’Ohm en courant continu : U_AB = R . I

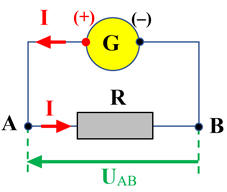
-  En courant variable, la loi d’Ohm est toujours valable,

-  On oriente le circuit, ainsi on peut écrire la loi d’Ohm :

-  Avec l’orientation choisie : u_AB = R . i

-  Remarque : u_BA = – u_AB = – R . i

II- Le condensateur.

1)- Constitution d’un condensateur.

a)-  Description :

-  Un condensateur est formé de deux conducteurs métalliques appelés armatures, séparés par un isolant qui peut être de l'air ou un diélectrique.

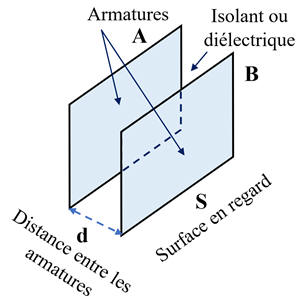
-  Le plus utilisé et le plus connu des condensateurs est le condensateur plan.

b)-  Symbole d’un condensateur :

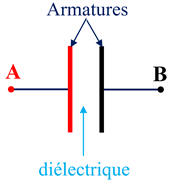
c)-  Exemples de condensateurs :

d)-  Champ électrique dans un condensateur plan chargé.

-  Considérons le condensateur suivant :

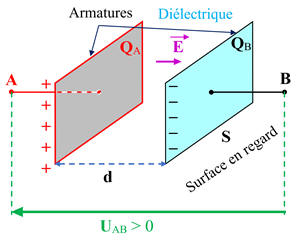
-  Pour charger un condensateur, on utilise un générateur de courant.

-  Schéma :

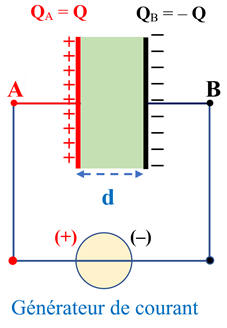
-  Le générateur transfère les électrons d’une armature sur l’autre.

-  On dit que le condensateur est chargé.

-  Le courant ne circule que lors de la charge.

-  Lorsque le condensateur est chargé, le courant ne circule plus.

-  L’armature reliée à la borne plus du générateur porte la charge + Q > 0 : + Q = Q_A

-  L’armature reliée à la borne moins du générateur porte la charge – Q < 0 : – Q = Q_B

-  Entre les armatures existe la tension U_AB = V_A – V_B >0

-  Q, grandeur positive, est appelée charge du condensateur.

-  C’est la charge portée par l’armature positive du condensateur :

-  + Q = Q_A = – Q_B

-  Dans l’espace situé entre les armatures, le champ électrique  :

-  Est considéré comme uniforme,

-  Sa direction est perpendiculaire aux armatures,

-  Son sens est dirigé de l’armature positive à l’armature négative (sens des potentiels décroissants),

-   

-  Son intensité (sa valeur) :

-  Schéma :

-  Dans le cas d’un condensateur plan, rempli d’un diélectrique de permittivité ε, dont la surface en regard des armatures est S, le champ électrique entre les armatures est donné par la relation :

-   

2)- Comportement d’un condensateur et capacité.

a)-  Charge d’un condensateur à courant constant.

►  Expérience.

-  Montage 1 : I₀ = 0,26 mA, R = 1 kW,  C = 1000 mF et U_max = 5 V

-  Enregistrement :

►  Explications.

-  Le générateur utilisé est un générateur de courant qui délivre une intensité constante I₀.

-  On temps t = 0 s, on bascule l'interrupteur sur la position 1 et on charge le condensateur.

-  Au cours de la charge, l'armature A présente un déficit d'électrons : q_A > 0

-  Au cours de la charge, l'armature B présente un excès d'électrons : q_B < 0

-  q_A = – q_B > à chaque instant.

-  Lorsque le condensateur est chargé, la valeur de l'intensité s'annule.

-  Représentation :

►  Exploitations.

-  Courbe u_AB = f(t) : la tension u_AB est proportionnelle à la durée Δt pendant la charge du condensateur.

-  Lorsque le condensateur est chargé, la tension u_AB = U ≈ 4,5 V

-  Courbe q_A = g (t) : la charge q_A est proportionnelle à la durée Δt pendant la charge du condensateur.

-  Lorsque le condensateur est chargé, la charge est constante : q_A = Q ≈ 4,5 mC

-  Remarque :

-   

-  La charge q_A est proportionnelle à la tension u_AB : q_A = k₁ . u_AB

b)-  Conclusion.

-  q_A = k₁ . u_AB 

-  Le coefficient de proportionnalité k₁ (grandeur positive) est appelé capacité du condensateur noté : C.

-  Représentation : convention récepteur.

-  On écrit :

-   

-  Cette relation est une relation algébrique, le signe de q_A est lié au signe de u_AB

►  remarque : capacité d'un condensateur plan :

-  Quelques permittivités relatives : 

-  E_max représente le champ disruptif.

-  Au-delà d'une certaine tension, le condensateur est détruit.

-  Il existe une tension de claquage (tension maximale de fonctionnement).

3)- Capteur capacitif.

-  Les capteurs capacitifs utilisent la mesure de la variation de diverses grandeurs comme :

-  La capacité, la charge des surfaces conductrices ou le champ électrique à l’intérieur du condensateur.

-  La capacité C d’un condensateur dépend de sa géométrie et de l’isolant entre ses armatures.

-  Si la capacité C varie en fonction d’une grandeur physique X, comme la position d ou l’accélération a alors sa mesure donne accès à la valeur de la grandeur X par la fonction X = f (C).

►  Fonctionnement d’un écran capacitif : écran d’un smartphone

-  La surface en verre d’un écran capacitif d’un smartphone comprend une grille de fils très fins chargée électriquement.

-  Lorsqu’un doigt touche l’écran des charges électriques sont transférées entre le doigt et l’écran.

-  Le champ électrique créé par les fils est localement modifié.

-  La détection de ces modifications permet au téléphone de localiser la zone de contact du doigt sur l’écran.

4)- Relation entre la charge électrique et la tension pour un condensateur.

-  Récapitulatif : Relations importantes :

-  Schéma ;

-  La charge q_A de l’armature A d’un condensateur est proportionnelle, à chaque instant, à la tension u_AB = u_C entre ses bornes :

-  L’intensité du courant est la dérivée, par rapport au temps, de la charge électrique q_A :

-  Comme q_A = C . u_AB :

-   

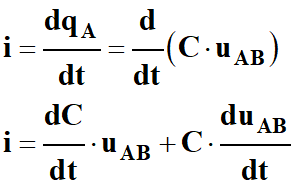
-  Comme la capacité C est une constante caractéristique du condensateur :

-   

-  On peut simplifier les notations :

-  On pose u_AB = u_C

-  Représentation symbolique du condensateur : Convention récepteur

►  Remarque :

-  Le signe de l’intensité du courant est lié au sens de variation de q_A charge portée par l’armature A et donc de celui de la tension u_C aux bornes du condensateur.

-  La grandeur  représente la dérivée par rapport au temps de la charge q_A

-  Si q_A augmente ⸕, alors

-  Si q_A diminue ⸔, alors

-  De même :

-  Si u_C augmente ⸕, alors

-  Si u_C diminue ⸔, alors

III- Le modèle du circuit RC série.

1)- Charge et décharge d’un condensateur.

a)-  Introduction

-  L’association en série d’un condensateur de capacité C et d’un conducteur ohmique de résistance R constitue un dipôle RC.

-  Schéma et notations :

b)-  Cas de la charge.

►  Expérience. (TP Physique N° 07)

-  Simulation avec Crocodile clips :

-  Charge d’un condensateur

-  Montage 1 : E = 4,0 V , R = 1,0 kΩ,  C = 1000 μF

-  Initialement, le condensateur est déchargé et l’interrupteur est en position 2 : u_C = 0 V

-  À la date t = 0 s, on bascule l’interrupteur sur la position 1.

►  Exploitation :

-  On obtient l’enregistrement suivant :

-  Courbe u_C = f (t) :

-  La tension u_C augmente au cours du temps.

-  Il existe un régime transitoire qui correspond à la charge du condensateur et un régime permanent lorsque le condensateur est chargé.

-  Lorsque le condensateur est chargé, la tension u_C ≈ 4,0 V

-  C’est la tension délivrée par le générateur idéal de tension.

►  Établissement de l’équation différentielle vérifiée par la tension u_C :

-  Loi d’Ohm aux bornes du conducteur ohmique : u_R = R . i

-  Relations pour le condensateur :

-  Loi des mailles (additivité des tensions) :

-  E = u_R + u_C

-  E = R . i + u_C avec

-  On en déduit l’équation différentielle vérifiée par la tension u_C lors de la charge :

-   

►  Solution de l’équation différentielle vérifiée par la tension u_C lors de la charge :

-  Les solutions d’une équation différentielle y’ = a . y + b avec a ≠ 0,  sont de la forme :

-   

-  La constante K est liée aux conditions initiales.

-  Les constantes a et b sont liées aux caractéristiques du circuit.

-  En utilisant la formulation précédente :

-   

-  Avec comme solution :

-   

-  On en déduit que :

-   

-  Recherche de l’expression de K :

-  Au temps t = 0 s, u_C (0) = 0 le condensateur est déchargé :

-   

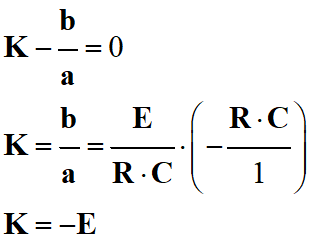
-  Solution de l’équation différentielle :

-   

-  le produit R . C représente le temps caractéristique (constante de temps) du dipôle RC série.

-  Il a la dimension d'un temps.

►  Allure de la courbe :

c)-  Cas de la décharge.

►  Expérience. (TP Physique N° 07)

-  Simulation avec Crocodile clips :

-  Décharge d’un condensateur

-  Montage 1 : E = 4,0 V , R = 1,0 kΩ,  C = 1000 μF

-  Initialement, le condensateur est chargé et l’interrupteur est en position 1 : u_C = 4,0 V

-  À la date t = 0 s, on bascule l’interrupteur sur la position 2.

►  Exploitation :

-  On obtient l’enregistrement suivant :

-  Courbe u_C = f (t) :

-  La tension u_C diminue au cours du temps.

-  Il existe un régime transitoire qui correspond à la décharge du condensateur et un régime permanent lorsque le condensateur est totalement déchargé.

-  Lorsque le condensateur est déchargé, la tension u_C ≈ 0,0 V

►  Établissement de l’équation différentielle vérifiée par la tension u_C :

-  Loi d’Ohm aux bornes du conducteur ohmique : u_R = R . i

-  Relations pour le condensateur :

-  Loi des mailles (additivité des tensions) :

-  u_R + u_C = 0

-  R . i + u_C = 0 avec

-  On en déduit l’équation différentielle vérifiée par la tension u_C lors de la décharge :

-   

►  Solution de l’équation différentielle vérifiée par la tension u_C lors de la décharge :

-  Les solutions d’une équation différentielle y’ = a . y + b avec a ≠ 0,  sont de la forme :

-   

-  La constante K est liée aux conditions initiales.

-  Les constantes a et b sont liées aux caractéristiques du circuit.

-  En utilisant la formulation précédente :

-   

-  Avec comme solution :

-   

-  On en déduit que :

-   

-  Recherche de l’expression de K :

-  Au temps t = 0 s, u_C (0) = E :  le condensateur est chargé :

-  K = E

-  Solution de l’équation différentielle :

-   

►  Allure de la courbe :

2)- Charge et décharge d’un condensateur

-  Simulation avec Crocodile clips :

-  Graphe :

-  Montage 3 : C = 0,5 mF, R = 1 kW et f = 100 Hz à 50 Hz.

-  Oscillogramme :

-  Observations :

-  la courbe 2 représente un « échelon de tension ».

-  La courbe 1 montre que la tension aux bornes du condensateur augmente au cours du temps.

-  La charge du condensateur n'est pas instantanée.

-  Il existe un régime transitoire (charge du condensateur) et un régime permanent (condensateur chargé).

-  Le condensateur d’un dipôle (R, C) soumis à un échelon de tension ne se charge pas instantanément : la charge d’un condensateur est un phénomène transitoire.

3)- Temps caractéristique.

-  La durée de charge du condensateur d'un dipôle (R, C) dépend de la résistance R du conducteur ohmique et de la capacité C du condensateur.

-  τ = R . C

-   La durée de charge du condensateur augmente avec la valeur du produit r . C.

-  « Analyse dimensionnelle » :

-  Notations :

-  La notation [R] représente la  grandeur physique (dans le cas présent la résistance d’un conducteur ohmique.

-  La notation (Ω) représente l’unité.

-  Ainsi l’écriture [R] = (Ω) indique que la résistance d’un conducteur ohmique s’exprime en ohm.

-  Si on considère le produit R . C :

-   

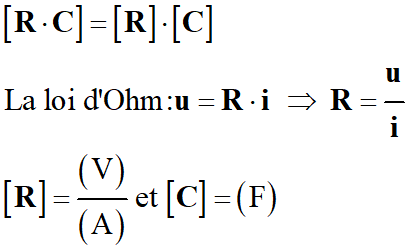
-  De la relation suivante , on tire :

-   

-  En conséquence :

-   

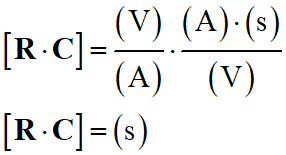
-  Autre méthode :

-   

-  Le produit R . C est bien homogène à un temps. Il représente une durée.

-  C’est une caractéristique du circuit RC série.

-  On l’appelle la constante de temps, notée τ :

-  τ = R . C

-  Le temps caractéristique τ (ou constante de temps) de la charge ou de la décharge d’un dipôle RC série est défini par la relation suivante :

►  Remarque :

-  Si on charge le condensateur pendant la durée Δt = τ , la charge Q_τ portée par le condensateur est égale à 63 % de sa charge maximale Q_max.

-  On écrit :

-  Si Δt = 5 τ , alors : .

-  Si on charge le condensateur pendant la durée Δt = τ , la tension aux bornes du condensateur est égale à 63 % de sa tension maximale U_max = E.

-   

-  Si Δt = 5 τ , alors : .

►  Exemple : R = 10 kΩ et C = 0,10 μF, τ = R . C = 1,0 ms.

-  On peut considérer qu'au bout de 5,0 ms, le condensateur est chargé.

-  La constante de temps τ d'un circuit (R, C) permet de connaître l'ordre de grandeur de la durée de charge d'un condensateur.

4)- détermination expérimentale de la constante de temps τ.

a)- Cas de la charge d’un condensateur :

-  Montage 1 : E = 4,0 V , R = 1,0 kΩ,  C = 1000 μF

-  Valeur de la constante de temps :

-  τ = R . C

-  τ = 1,0 × 10³ × 1000 ×10^–6

-  τ ≈ 1,0 s

-  On peut considérer que le condensateur est chargé au bout de 5,0 s.

-  Initialement, le condensateur est déchargé et l’interrupteur est en position 2 : u_C = 0 V

-  À la date t = 0 s, on bascule l’interrupteur sur la position 1.

-  Recherche de l’expression littérale de :

-  Avec :

-  Loi des mailles :

-  E = u_R + u_C

-   

-  Au temps t = 0 s :

-   

-   

-  Pour déterminer graphiquement la valeur de τ, on trace la tangente à l’origine à la courbe u_C = f (t).

-  L’abscisse du point M d’intersection de la tangente avec l’asymptote horizontale donne la valeur de la constante de temps τ.

-  À partir du graphe : τ ≈ 1,0 s

b)- Cas de la décharge

-  Montage 1 : E = 4,0 V , R = 1,0 kΩ,  C = 1000 μF

-  Initialement, le condensateur est chargé et l’interrupteur est en position 1 : u_C = E =  4,0 V

-  À la date t = 0 s, on bascule l’interrupteur sur la position 2.

-  On obtient l’enregistrement suivant :

-  L’équation différentielle :

-      

-  Solution de l’équation différentielle :

-      

-  Dans ce cas :

-      

-  Pour déterminer graphiquement la valeur de τ, on trace la tangente à l’origine à la courbe u_C = f (t).

-  L’abscisse du point d’intersection de la tangente avec l'axe des abscisses donne la valeur de la constante de temps τ.

► Autre méthode (plus précise)

-  On détermine la valeur de la constante de temps τ par linéarisation :

-      

-  On représente la fonction ln (u_C) = g (t) :

-  On obtient une fonction affine du type y = a . t + b

-  La grandeur τ = R . C est égale à l’opposé de l’inverse du coefficient directeur a de la droite ln (u_C) = g (t).

-  Graphe :  

-  Coefficient directeur :

-  Ordonnée à l'origine :  b = ln (E)

-      

IV- Applications.

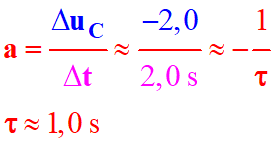
1)- Charge et décharge d’un condensateur.

-  Le circuit (R, C) (CONDO).

-  Charge d’un condensateur.

-  Le circuit (R, C) (CASSY LAB).  

2)- QCM.

3)- Exercices.