|
Phys. N° 06 |
Le dipôle (R, C). Cours. |
|
|
|
|
Programme 2012 : Physique et Chimie Programme 2020 : Physique et chimie |
Pour aller plus loin :
|
Mots clés :
Récepteur et générateur ; convention récepteur ; convention générateur ; e circuit électrique ; orientation d'un circuit électrique ; loi d'Ohm ; le conducteur ohmique ; résistance d'un conducteur ohmique ; le condensateur ; capacité d'un condensateur ; charge et décharge d'un condensateur ; énergie d'un condensateur ; constante de temps d'un circuit RC ; ... |
I-
Rappels sur l’orientation d’un circuit.![]()
1)- Orientation d’un circuit et d’un dipôle.
- Pour pouvoir étudier le comportement électrique d’un dipôle électrique, il faut l’orienter le circuit ou la branche de circuit dans lequel il se trouve.
- On choisit dans le circuit série ou la branche d’un circuit un sens d’orientation arbitraire.

- Le dipôle est orienté de A vers B.
- Un courant électrique résulte d’un mouvement ordonné de porteurs de charge (les électrons dans un métal et les ions d’un un électrolyte).
- La mesure du débit de charges, exprimée en ampère (A), donne l’intensité du courant i qui est une grandeur algébrique.
- Si le courant circule dans le sens de la flèche alors i est positif, sinon, il est négatif.
- La tension uAB entre les bornes A et B d’un dipôle est égale à la différence de potentiel (VA – VB) entre ses deux points.
- La tension uAB , exprimée en volt (V), est représentée par une flèche tracée hors du circuit et orientée de B vers A.

|
- Convention récepteur : En convention récepteur, la flèche précisant l’orientation du dipôle est en sens contraire par rapport à la flèche utilisée pour représenter la tension uAB. |
3)- Courant et tension continus et courant et tensions variables.
- En courant continu, l’intensité du courant est constante. On la note avec une lettre Majuscule I.
- Elle correspond à un débit de charges électriques.
- La quantité d’électricité Q qui traverse une portion de circuit pendant la durée Δt est donnée par la relation :
|
|
|
|
Q = n . e charge en coulomb (C) |
||||
|
Q = I . Δt |
=> |
|
I intensité en ampère (A) |
||||
|
|
|
|
Δt durée en seconde (s) |
- De même une tension continue entre deux points A et B d’un circuit se note : UAB.
- Les courants et les tensions sont qualifiés de variables si leurs valeurs varient au cours du temps.
- On note ses grandeurs à l’aide de lettres minuscules : i pour l’intensité et uAB pour la tension entre deux points A et B d’un circuit.
- La loi d’additivité des tensions et la loi des nœuds sont vérifiées lorsque les circuits sont parcourus par des courants variables.
4)- Le conducteur ohmique : Loi d’Ohm.
- Rappel de première : en courant continu et dans un circuit simple ne comportant qu’un générateur, le sens du courant est défini de la borne (+) vers la borne (–)
- Par commodité, on oriente le dipôle en utilisant le sens du courant dans le circuit :
- On peut écrire la loi d’Ohm en courant continu : UAB = R . I

- En courant variable, la Loi d’Ohm est toujours valable, le fait d’orienter le circuit permet de pouvoir écrire la loi d’Ohm :
- Dans le cas présent : uAB = R . i

- Remarque : uBA = - uAB = – R . i
- Un condensateur est formé de deux conducteurs métalliques appelés armatures, séparés par un isolant qui peut être de l'air ou un diélectrique.

- Le plus utilisé et le plus connu des condensateurs est le condensateur plan.
2)- Symbole d’un condensateur :

III-
Charge d’un condensateur. (TP Physique N° 06)![]()
1)- Expérience. Logiciel Condo et carte Candibus.
- Montage 1 : E = 4,0 V , R = 1 kΩ, C = 1000 μF

- Le générateur utilisé est un générateur de courant qui délivre une tension constante E.
- On temps t = 0 s, on bascule l'interrupteur sur la position 1 et on charge le condensateur.
- Au cours de la charge, l'armature A se charge positivement. Elle présente un déficit d'électrons qA > 0.
- Au cours de la charge, l'armature B se charge négativement. Elle présente un excès d'électrons : qB < 0.
- q A = – qB à chaque instant.
- Par définition, la quantité qA = – qB représente la charge du condensateur.
- C’est une grandeur positive. Elle s’exprime en Coulomb C.
- On l’appelle aussi ; quantité d’électricité emmagasinée.
- Une tension uAB apparaît entre les plaques A et B lorsque le condensateur se charge.
- Lorsque le condensateur est chargé, la valeur de l'intensité s'annule et la tension uAB prend sa valeur maximale.
- Le but est de rechercher la relation qu’il existe entre l’intensité du courant et les charges portées par les armatures.
- Premier cas :
- considérons que le condensateur porte la charge qA à l’instant t et que pendant l’intervalle de temps dt, le courant circule dans le sens indiqué par la flèche.
- Pendant la durée très courte dt, la charge varie de dqA = qA (t + dt) – qA (t)

- Le courant circule dans le sens arbitraire choisi :
- 
- deuxième cas :
- considérons que le courant circule dans le sens inverse du sens indiqué par la flèche.
- Pendant la durée très courte dt, la charge varie de dqA.
- Le courant circule dans le sens inverse du sens arbitraire choisi :
- 
- Par définition, l’intensité du courant dans un fil conducteur
correspond au débit de charges transportées :
- On écrit que :

- Remarque : Cette relation découle de la relation suivante
Q =
I .
Δt
valable en courant continu.
- Si pendant la durée Δt, la variation de charge est Δq, on peut définir l’intensité moyenne comme le rapport suivant :
-  .
.
- En courant variable, on peut définir l’intensité instantanée.
- L’intensité instantanée est égale à la dérivée par rapport au
temps de la charge transportée :
- 
IV-
Charge à intensité constante. (TP Physique N° 06)![]()
Le but est de trouver la relation qui existe entre la tension aux bornes du condensateur et la charge du condensateur.
- Logiciel : Logiciel Condo et carte Candibus.
- Montage 1 : I0 = 0,26 mA, R = 1 kΩ, C = 1000 μF et U max = 5 V

- Un générateur de courant délivre une intensité constante pendant la durée de la charge.
- On mesure la valeur de la tension uAB au cours du temps.
- Connaissant la valeur de l’intensité, on en déduit celle de la charge qA de l’armature A au cours du temps car : qA = I . Δt
- Courbe u AB = f (t) :
- La tension uAB est proportionnelle à la durée Δt pendant la charge du condensateur.
- Lorsque le condensateur est chargé, la tension uAB ≈ 4,5 V.

- Courbe qA = g (t) :
- La charge qA est proportionnelle à la durée Δt pendant la charge du condensateur.
- Lorsque le condensateur est chargé, la charge est constante : qA = Q ≈ 4,5 mC.

- Remarque :
- 
- La charge qA est proportionnelle à la tension uAB :
- qAB = k1 .uAB
- Courbe qA = h (uAB) :

- Le tracé du graphe représentatif de qA en fonction de uAB est une droite de coefficient directeur positif passant par l’origine.
- Ceci est bien en accord avec le résultat trouvé précédemment.
- En conséquence :
- La charge qA de l’armature A du condensateur est proportionnelle à la tension uAB entre ses armatures.
- qAB = C . uAB
- C est appelée la capacité du condensateur.
- Elle s’exprime en farad (F).
- La charge
qA
de l’armature
A s’exprime en coulomb (C).
- La tension uAB s’exprime en volt (V).
- Représentation :
convention
récepteur :


V-
Charge d’un condensateur par un échelon de tension.
(TP Physique N° 06)![]()
1)- Dipôle (R, C) soumis à un échelon de tension.
- Un échelon de tension E est le passage instantané d'une tension de valeur nulle à une tension de valeur constante E.
- Représentation :

- tension aux bornes du générateur de tension : U = E ≈ 4,00 V.
- Logiciel : Logiciel Condo et carte Candibus.
- Montage 1 : R = 1 kΩ, C = 1000 μF et U = 4 V

- Courbe uAB = f (t) :
- La tension uAB augmente au cours du temps.
- Il existe un régime transitoire qui correspond à la charge du condensateur et un régime permanent lorsque le condensateur est chargé.
- Lorsque le condensateur est chargé, la tension uAB ≈ 4 V.
- C’est
la tension délivrée par le générateur idéal de tension.

- Courbe qA = g (t) :
- La charge qA augmente au cours du temps.
- Il existe un régime transitoire qui correspond à la charge du condensateur et un régime permanent lorsque le condensateur est chargé.
- Lorsque le condensateur
est chargé, la charge
qA
≈ 4 mC.

- Courbe qA = h (uAB) :
- La charge qA de l’armature A du condensateur est proportionnelle à la tension uAB entre ses armatures.
- q A = C . uAB : C est appelée la capacité du condensateur.
- Elle s’exprime en farad (F).

- Courbe : i = f1 (t) :
- L’intensité est une fonction décroissante du temps.
- La valeur maximale de imax ≈ 4 mA.
- L’intensité du courant décroît au cours du temps et s’annule lorsque le condensateur est chargé.
- Il existe toujours deux phases : le régime transitoire et le régime permanent.

4)- Facteurs intervenant sur la durée de la charge.
- Montage (‘’simulation’’ d’un échelon de tension à l’oscilloscope) :
- Ou simulation avec excel fichier : charge d’un condensateur u.
- Simulation
avec Crocodile clips : fichier :
charge d’un condensateur u.
- C = 0,5 μF, R = 1 kΩ et f = 100 Hz à 50 Hz.

- Oscillogramme :

- Observations : la courbe 2 représente un échelon de tension.
- La courbe 1 montre que la tension aux bornes du condensateur augmente au cours du temps.
- La charge du condensateur n'est pas instantanée.
- Il existe un régime transitoire (charge du condensateur) et un régime permanent (condensateur chargé).
- Le condensateur d’un dipôle (R, C) soumis à un échelon de tension ne se charge pas instantanément :
- La charge d’un condensateur est un phénomène transitoire.
- La durée de charge du condensateur d'un dipôle (R, C) dépend de la résistance du conducteur ohmique et de la capacité du condensateur.
- La durée de charge du condensateur augmente avec la valeur du produit R.C.
- On appelle constante de temps du circuit (R, C), la valeur : τ = R.C.
- τ constante de temps : seconde s.
- R résistance du conducteur ohmique ohm Ω.
- C capacité du condensateur : farad F.
- Analyse dimensionnelle :
- 
- Le produit R.C est bien homogène à un temps.
- Remarque :
- Si on charge le condensateur pendant la durée Δt = τ, la charge Qτ portée par le condensateur est égale à 63 % de sa charge maximale Q max.
- On écrit :

- Si
Δt = 5
τ
, alors :
 .
.
- Exemple :R = 10 kΩ et C = 0,10 μF, τ = R.C = 1,0 ms.
- On peut considérer qu'au bout de 5 ms, le condensateur est chargé.
- La constante de temps τ d'un circuit (R, C) permet de connaître l'ordre de grandeur de la durée de charge d'un condensateur.
- On reviendra sur ces résultats lors de l'étude théorique.
a)- Schéma du montage :

- Pour trouver l'équation différentielle, il faut orienter le circuit, écrire la loi d'Ohm aux bornes de chaque dipôle et utiliser l'additivité des tensions.
- Loi d’ohm aux bornes du conducteur ohmique : uDA = R . i
- Loi d’ohm aux bornes du condensateur :
-

- Relation entre l’intensité i et la tension uAB :
-

- Loi d’additivité des tensions :
- 
c)- Solution :
- On reconnaît une équation différentielle du premier ordre avec deuxième membre qui admet une solution du type :
- uAB (t) = A . e k. t + B où A, B et k sont des constantes.
d)- Détermination des constantes.
- On détermine les constantes à l’aide des conditions initiales et des paramètres du circuit.
- Première étape : on reporte l’expression de la solution dans l’équation (1).
- 
- La solution uAB (t) = A . e k. t + B vérifie l’équation différentielle (1).
- Expression de
![]() :
:

- On remplace
![]() et
uAB
par leur expression respective dans l’équation (1).
et
uAB
par leur expression respective dans l’équation (1).
- 
- La relation (2) est vérifiée à chaque instant.
- Or E = cte, B = cte et t et par conséquence e k. t varient au cours du temps.
- Il faut nécessairement que :
|
{ |
(1 + R . C . k) . A = 0 |
=>
|
{
|
|
||||
|
E = B |
E = B |
|||||||
|
La solution A = 0 n'a pas de signification physique |
||||||||
- conditions initiales : au temps t = 0 s, la tension aux bornes du condensateur est nulle : uAB (0) = 0
- On déduit de ceci que : A + B = 0 => A = – B = – E.
- Il vient :
- 
- En utilisant le fait que τ = RC constante de temps du circuit,
- ![]()
- vérification :
-
![]()
- Signification de la constante de temps τ.
- Remarque :
- on charge le condensateur pendant la durée Δt = τ, donner l’expression de uAB en fonction de E.
- 
- On en déduit qu’ au bout du temps τ :
- 
- Si Δt = 5 τ ,
- 
- alors, au bout du temps 5 τ :
-

- Le condensateur est chargé à plus de 99 %.
- Intensité de charge :
- 
6)- détermination expérimentale de la constante de temps τ.
- On trace la tangente à la courbe au point d'abscisse t = 0 s et l'asymptote horizontale.
- La constante de temps τ est donnée par l'abscisse de leur point d'intersection.

- Démonstration :
- Expression littérale de
 : sachant que
: sachant que

- additivité des tensions E = uDA + uAB = R . I + uAB (1)
- 
- Au temps t = 0 s :
-

|
Pour déterminer graphiquement la valeur de τ, on trace la tangente à l’origine à la courbe uAB = f (t) et l’asymptote horizontale à cette courbe. L’abscisse du point d’intersection de ces deux droites donne la valeur de la constante de temps τ. |
- Remarque : on peut utiliser le fait que :
 ou
ou
 .
.

VI-
Décharge d’un condensateur.![]()
a)- Montage :
- Première étape : on charge le condensateur : Interrupteur sur la position 1

- Deuxième étape : on décharge le condensateur :Interrupteur sur la position 2

- Le condensateur est déchargé.

b)- Les courbes qA = f (t) et i = g (t).
c)- Interprétation.
- La tension uDA = R.i, positive lors de la charge, est négative lors de la décharge.
- L'intensité du courant positive lors de la charge est négative lors de la décharge.
- Le courant circule dans le sens inverse du sens positif choisi.
- Le courant a changé de sens lors de la décharge.
- L’armature B perd des électrons et l’armature A, initialement chargée positivement gagne des électrons et sa charge diminue.
- La tension uAB positive lors de la charge reste positive lors de la décharge et diminue progressivement pour s’annuler en même temps que le courant.
- Le passage du courant lors de la décharge correspond à un régime transitoire.
- La tension aux bornes du condensateur ne subit pas de discontinuité alors que l’intensité du courant subit une discontinuité.

- Loi d’ohm aux bornes du conducteur ohmique uDA = R.i
- Loi d’ohm aux bornes du
condensateur :

- Relation entre l’intensité et la tension
u
AB :

- 
- La solution de cette équation différentielle est de la forme générale : uAB (t) = A . e k . t
- Dans le cas présent, on trouve que la solution est :
-
![]()
- expression de l’intensité de décharge :
- 
- Avec l’orientation choisie pour le circuit, l’intensité est négative au cours de la décharge.
VII-
Énergie emmagasinée dans un condensateur.![]()
- Montage :

- On charge un condensateur de capacité C = 4700 μF puis on le décharge dans un moteur électrique.
- Le moteur tourne lors de la décharge du condensateur et fait remonter une charge de masse m.
- Au cours de la charge, un condensateur emmagasine de l'énergie. Cette énergie est restituée lors de la décharge.
- Un condensateur de capacité C chargé sous la tension u emmagasine l’énergie :
- 
- EC : énergie en joule J
- C capacité en farad F
- u tension aux bornes du condensateur en volt V.
- C’est de l'énergie potentielle électrostatique :
- Remarque : le transfert d’énergie ne peut pas se faire instantanément.
- La constante de temps τ donne un ordre de grandeur de cette durée.
- L’énergie n’évolue pas brutalement comme la tension.
VIII-
Applications. Exercices : 5, 11, 17, 18, 22, 24 pages 166 – 169.![]()
1)- Énergie d'un condensateur.
- On charge un condensateur (voir montage 5).
- On donne C = 10 μF et U = 100 V.
- Calculer l'énergie emmagasinée par le condensateur.
- On décharge le condensateur.
- On convertit intégralement cette énergie en énergie mécanique pour faire fonctionner un moteur.

- De quelle hauteur h peut-on faire monter une charge de masse m = 20 g.
- On considère que les pertes d’énergie sont négligeables.
2)- Exercices : 5, 11, 17, 18, 22, 24 pages 166 – 169.
- Le condensateur : Énoncé (Word zip)
IX-
Visualisations à l’oscilloscope.![]()
- Montage 1 : C = 0,5 μF et R = 500 Ω et f = 200 Hz

- Oscillogramme :

- À la voie A de l'oscilloscope, on visualise les variations de la tension uAM = uR en fonction du temps.
- Or, uAM = R . i, on visualise les variations de l'intensité en fonction du temps ceci à une constante près.
- À la voie B de l'oscilloscope, on visualise les variations de la tension uBM en fonction du temps.
- Si l'on appuie sur la touche -B, on visualise les variations de uMB = uC.
- Si l'on se place au temps tc, lorsque la charge du condensateur commence, la tension uAM > 0 V et le courant circule de A vers B.
- On remarque que la valeur de l'intensité i du courant diminue au cours du temps et tend vers zéro lorsque le condensateur est chargé.
- 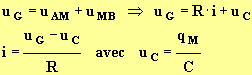
- Or au temps t = 0 s, le condensateur est déchargé :
- 
- Le régime permanent est atteint si : uC = uMB = E => i = 0 A
- La charge q ne subit pas de discontinuité alors que l'intensité i subit une discontinuité (lors de la décharge, le courant change de sens).
22)- Remarque : cas d'un circuit (R, C).
- Montage 2 : C = 10 nF, R = 0,5 kΩ et f = 1500 Hz.

- 
- Oscillogramme : à finir !!
- Conclusion :