Chap. N° 21 Exercices 2024 : Dynamique du dipôle RC cours

Chap. N°21

Dynamique du dipôle RC

Exercices 2024
Cours

Exercices

I- Exercice : Charger un condensateur à courant constant.

1)- Énoncé.

2)- Correction.

II- Exercice : Étudier la charge d’un condensateur par des mesures manuelles.

1)- Énoncé.

2)- Correction.

III- Exercice : Microphone électrostatique à condensateur.

1)- Énoncé.

2)- Correction.

IV- Exercice : Temporisation d’une alarme.

1)- Énoncé.

2)- Correction.

V- Exercice : Un accéléromètre pour sauver des vies.

I- Exercice : Charger un condensateur à courant constant.

1)- Énoncé.

La charge d’un condensateur se fait avec un générateur de courant délivrant un courant d'intensité constante I₀ = 0,010 mA.

La représentation graphique de l'évolution de la tension u_C aux bornes du condensateur en fonction du temps est donnée ci-dessous :

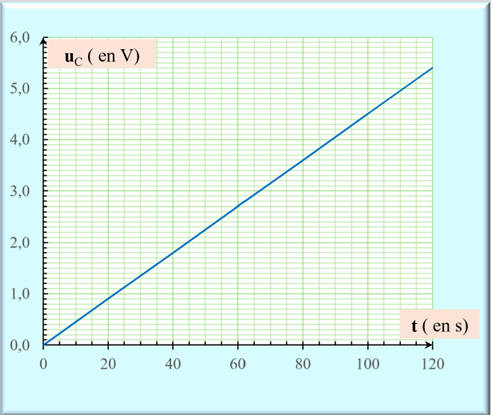
graphe uC = f (t)

a)- Donner l'expression de la charge q (t) stockée dans le condensateur à la date t en fonction de Δt et de I₀.

b)- En déduire l'expression de la tension u_C (t) en fonction de I₀, Δt et de la capacité C du condensateur.

c)- Déterminer la valeur de la capacité C du condensateur en μF.

2)- Correction.

a)- Expression de la charge q (t) stockée dans le condensateur à la date t en fonction de Δt et de I₀.

- Schéma du montage :

Charge d’un condensateur à courant constant

- Le générateur utilisé est un générateur de courant qui délivre une intensité constante I₀.

- On temps t₀ = 0 s, on bascule l'interrupteur sur la position 1 et on charge le condensateur.

- Au cours de la charge, l'armature A présente un déficit d'électrons : q_A> 0

- Au cours de la charge, l'armature B présente un excès d'électrons : q_B< 0

- q_A= – q_B> à chaque instant.

- Lorsque le condensateur est chargé, la valeur de l'intensité du courant s'annule.

- Représentation symbolique du condensateur :

condensateur

► Exploitation de la courbe.

- Courbe u_C = f (t) : la tension u_C est proportionnelle à la durée Δt pendant la charge du condensateur.

- Charge q (t) stockée dans le condensateur à la date t en fonction de Δt et de I₀

- q (t) = q_A = I₀ . Δt

- La grandeur q (t), que l’on note aussi q_C (t), est la charge portée par l’armature A.

b)- Expression de la tension u_C (t) en fonction de I₀, t et de la capacité C du condensateur.

- Représentation : Convention récepteur.

condensateur

- Avec : u_AB = u_C

- On écrit :

- Cette relation est une relation algébrique, le signe de q_A = q_C est lié au signe de u_AB = u_C


u_AB = u_C	Tension aux bornes du condensateur en volt (V)
q_A = q_C	Charge de l’armature A du condensateur en coulomb (C)
C	Capacité du condensateur en farad (F, μF, nF ou pF)

c)- Valeur de la capacité C du condensateur en μF.

- q (t) = q_A = I₀ . Δt

- Exploitation de la courbe u_C (t) = f (t)

- La courbe est un segment de droite passant par l’origine.

- On en déduit, que dans le domaine étudié, la tension u_C (t) est proportionnelle à la durée Δt.

- u_C (t) = k . Δt

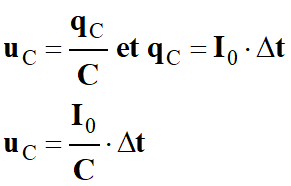
- uC = I0 . Dt / C

- Remarque :

- Δt = t – t₀ avec t₀ = 0 s

- Δt = t

- On tire l’expression suivante :

- La grandeur k représente la valeur du coefficient directeur du segment de droite .

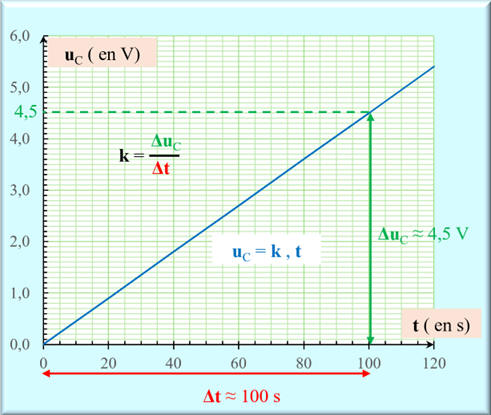
exploitation du graphe uC = f (t)

- Valeur de k :

- k = 0,045 V / s

- Valeur de la capacité du condensateur :

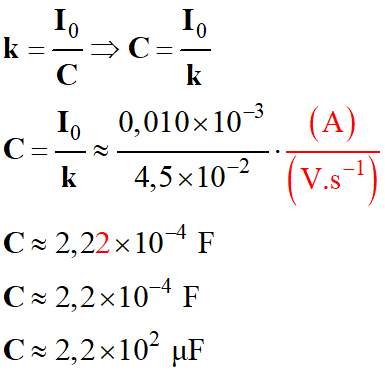
- C = 220 microfarad

- Soit environ 220 μF

- Remarque : les unités :

- q (t) = q_A = I₀ . Δt

- q (t) = q_A = C . u_C

- I₀ . Δt = C . u_C

- Explication : [C] = (F)

- La notation [C] représente la grandeur physique et la notation (F) représente son unité

- Tractuction : La capacité C d'un condensateur s'exprime en farad (F)

- unités

II- Exercice : Étudier la charge d’un condensateur par des mesures manuelles.

1)- Énoncé.

Un étudiant en physique a récupéré plusieurs supercondensateurs sur une visseuse électrique à charge rapide défectueuse.

Il cherche à savoir si l'un des condensateurs, utilisable pour réaliser une lampe USB expérimentale, et si oui quelle est l'heure de sa capacité C.

L’étudiant ne dispose que d'un simple multimètre, une pile de 4,5 V, une résistance 100 Ω et du fil de cuivre pour réaliser un circuit et mesurer l'évolution de la tension u_C du condensateur au cours du temps durant sa charge.

Il obtient le tableau de mesures suivant :

t (en s)	u_C (en V)
0	0,00
30	0,82
60	1,48
90	2,02
120	2,49
150	2,84
180	3,14
250	3,64
350	4,07
500	4,34
800	4,48
1100	4,50
1500	4,50

a)- Réaliser le schéma électrique du circuit utilisé par l'étudiant.

b)- Justifier que le composant se comporte bien comme un condensateur.

c)- Mettre en œuvre l'une des méthodes graphiques pour déterminer C.

2)- Correction.

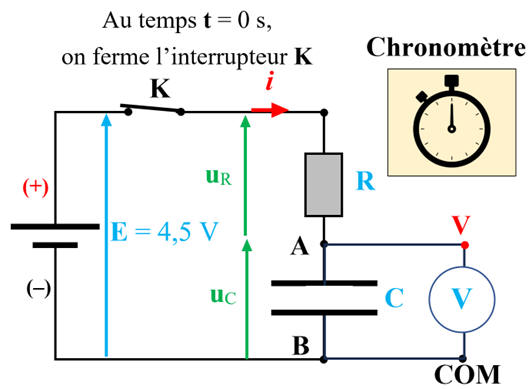
a)- Schéma électrique du circuit utilisé par l'étudiant.

- On considère que la pile est une source idéale de tension.

- Avant l’expérience, le condensateur est déchargé.

Schéma électrique du circuit utilisé par l'étudiant

b)- Étude de la charge du condensateur.

- Courbe obtenue :

- Initialement le condensateur est déchargé et la tension u_C à ses bornes est nulle.

- Ceci est caractéristique d’un condensateur déchargé.

- Courbe u_C =f (t) :

- La tension u_C augmente au cours du temps.

- Il existe un régime transitoire qui correspond à la charge du condensateur et un régime permanent lorsque le condensateur est chargé.

- Au départ, la tension augmente rapidement, puis de plus en plus lentement

- Lorsque le condensateur est chargé, la tension u_C ≈ 4,5 V et l’intensité dans le circuit est nulle

- C’est la tension délivrée par le générateur idéal de tension.

- Ceci montre que la tension aux bornes du conducteur ohmique u_R de résistance R est nulle.

- Ce comportement est caractéristique du comportement d’un condensateur.

c)- Méthodes graphiques pour déterminer C.

- On est en présence d’un circuit RC.

- Ce type de circuit est caractérisé par une constante de temps τ :

- Le temps caractéristique τ (ou constante de temps) de la charge ou de la décharge d’un dipôle RC série est défini par la relation suivante :

τ = R . C
τ	Constante de temps ou temps caractéristique en seconde (s)
R	Résistance du conducteur ohmique en ohm (Ω)
C	Capacité du condensateur en farad (F, μF, nF ou pF)

- Expression de la constante de temps :

- τ = R . C

- On connait la valeur de la résistance R du conducteur ohmique.

- La connaissance de la valeur de la constante de temps permet de déterminer la valeur de la capacité C du condensateur.

- Détermination graphique de la constante de temps :

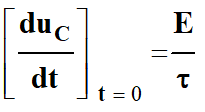- dérivée Comment démontrer cette relation ? : lien

- Pour déterminer graphiquement la valeur de τ, on trace la tangente à l’origine à la courbe u_C = f (t).

- L’abscisse du point M d’intersection de la tangente avec l’asymptote horizontale donne la valeur de la constante de temps τ.

- À partir du graphe : τ ≈ 1,5 × 10² s

- Valeur de la capacité du condensateur :

- τ = R . C

- C = 1,5 F

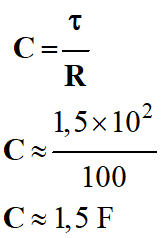
- C’est un gros condensateur.

► Autre méthode :

- Si on charge le condensateur pendant la durée Δt = τ , la tension aux bornes du condensateur est égale à 63 % de sa tension maximale U_max = E.

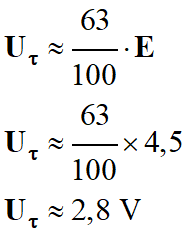
- Utau = 2,8 V

- On trouve la même valeur pour la constante de temps τ.

- Cette méthode est plus précise que celle qui utilise le tracé de la tangente à l’origine.

- Pour plus de précision, il vaut mieux utiliser les deux méthodes simultanément.

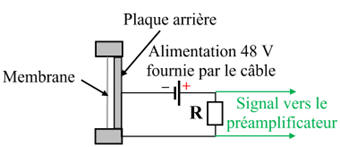
III- Exercice : Microphone électrostatique à condensateur.

1)- Énoncé.

Un microphone électrostatique à condensateur est constitué d'une très fine membrane métallique ou de mylar métallises qui constitue l'une des armatures d'un condensateur.

Cette membrane peut se déplacer sous l'effet des variations de la pression acoustique engendrée par une onde sonore.

Elle est située à 20,0 μm d’une plaque métallique fixe qui constitue l'autre armature du condensateur.

L'air emprisonné entre les 2 armatures joue le rôle d'isolant.

Microphone électrostatique à condensateur

Schéma :

Microphone électrostatique à condensateur : schéma

L’expression de la capacité C du condensateur constitué des 2 armatures, séparées d’une distance e et dont les surfaces en regard ont chacune une aire S, est :

a)- Vérifier que la capacité C, du condensateur, est égale à 224 pF pour des armatures de diamètre égal à un pouce soit à 2,54 cm.

b)- Déterminer la variation de capacité lorsque la membrane s'enfonce de 0,010 μm sous l'effet d'une variation de pression due à une onde sonore.

c)- En déduire la variation de charge portée par l'une des armatures du condensateur soumis à une tension constante E = 48 V.

d)- La variation de pression produite par l'onde sonore émise par le chanteur se produit pendant une durée de l'ordre de 2,0 ms.

Estimer l'ordre de grandeur de l'intensité i du courant électrique traversant le circuit.

e)- En déduire l'ordre de grandeur de la tension électrique aux bornes de la résistance R = 1,0 MΩ et

justifier la nécessité d’un préamplificateur pour augmenter l'amplitude du signal produit par le microphone.

2)- Correction.

a)- Valeur de la capacité C du condensateur.

- C = 224 pF

- diamètre des armatures : d = 2,54 cm

- Distance entre les armatures : e = 20,0 μm

- Relation donnée dans l’énoncé :

- Aire de la surface S :

- Valeur de la capacité du condensateur :

- C = 224 pF

- La valeur trouvée est bien en accord avec celle proposée dans l’énoncé.

b)- Variation de capacité lorsque la membrane s'enfonce de 0,010 μm.

- Distance entre les armatures : e’ = e – Δe

- Distance entre les armatures : e = 20,0 μm

- Enfoncement de la membrane : Δe = 0,10 μm

- Expression de la capacité C du condensateur pour l’écartement e :

- Expression de la capacité C’ du condensateur pour l’écartement e’ = e – Δe :

- Variation ΔC de la valeur de la capacité du condensateur :

- ΔC = C’ – C

- Variation ΔC de la valeur de la capacité du condensateur

- En utilisant le fait que :

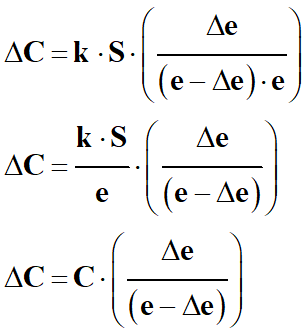
- Variation ΔC de la valeur de la capacité du condensateur

- D’autre part, on peut considérer que Δe << e :

- On peut utiliser la relation approchée suivante :

- Variation ΔC de la valeur de la capacité du condensateur : relation approchée

- Application numérique :

- DC = 0,11 pF

c)- Variation de charge portée par l'une des armatures du condensateur

- Tension aux bornes du condensateur :

- Tension constante E = 48 V.

- Modélisation du circuit :

- Schéma normalisé du condensateur :

condensateur

- Relations importantes :


u_AB = u_C	Tension aux bornes du condensateur en volt (V)
q_A = q_C	Charge de l’armature A du condensateur en coulomb (C)
C	Capacité du condensateur en farad (F, μF, nF ou pF)

- q = C . u_C

- La tension aux bornes du condensateur est imposée par l’alimentation de tension E = 48 V.

- Variation de la charge portée par les armatures du condensateur :

- Δq = ΔC . u_C

- Δq = ΔC . E

- Application numérique :

- Δq ≈ 0,11 × 10^–12 × 48

- Δq ≈ 5,28 × 10^–12 C

- Δq ≈ 5,3 × 10^–12 C

d)- Ordre de grandeur de l'intensité i du courant électrique traversant le circuit.

- La variation de pression produite par l'onde sonore émise par le chanteur se produit pendant une durée de l'ordre de 2,0 ms.

- L’intensité du courant i varie au cours du temps :

condensateur


q_A	Charge de l’armature A du condensateur en coulomb (C)
t	Temps en seconde (s)
i	Intensité du courant en ampère (A)

- Relation :

- On connait la variation Δq de charge pendant la durée Δt = 2,0 ms.

- On peut estimer la valeur de l’intensité moyenne i_moy pendant la durée Δt = 2,0 ms.

- Application numérique :

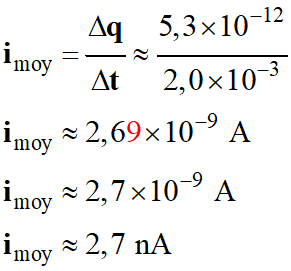
- imoy = 2,7 nA

- L’intensité i dans le circuit est de l’ordre de 3 nA environ.

- C’est une valeur d’intensité très faible.

e)- Ordre de grandeur de la tension électrique aux bornes de la résistance R = 1,0 MΩ.

- Schéma : tension aux bornes d’un conducteur ohmique parcouru par un courant électrique i :

association en série d’un condensateur de capacité C et d’un conducteur ohmique de résistance R

- u_R = R . i

- Ordre de grandeur de la valeur de la tension aux bornes du conducteur ohmique :

- u_R ≈ R . i_moy

- u_R ≈ 1,0 × 10⁶ × 2,7 × 10^–9

- u_R ≈ 2,69 × 10^–3 V

- u_R ≈ 2,7 × 10^–3 V

- u_R ≈ 2,7 mV

- La tension aux bornes du conducteur ohmique est de l’ordre de 3 mV.

- Cette tension est très faible.

- Il faut ajouter un préamplificateur pour augmenter l'amplitude du signal produit par le microphone et ainsi augmenter la valeur de la tension u_R.

IV- Exercice : Temporisation d’une alarme.

1)- Énoncé.

Après avoir mis sous tension l'alarme d'un appartement, il faut pouvoir disposer d'une durée suffisante pour sortir sans la déclencher.

Pour cela, certains dispositifs utilisent la charge et la décharge d'un condensateur.

Le circuit de l'alarme est alimenté par une batterie de tension à vide E et de résistance interne négligeable.

Le schéma simplifié du circuit électrique de l'alarme est le suivant :

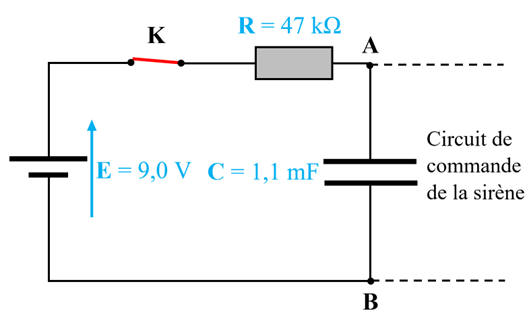
schéma simplifié du circuit électrique de l'alarme

La mise sous tension de l'alarme correspond à la fermeture de l'interrupteur K.

Le circuit de commande de la sirène est tel qu’à la fermeture de la porte de l'appartement, le condensateur est mis en court-circuit (ses armatures sont alors reliées par un fil conducteur non représenté sur le schéma).

1. Étude de la charge du condensateur dans le circuit RC.

- Pour étudier la charge du condensateur de capacité C, on enregistre l'évolution de la tension u_AB = f (t) entre ses bornes à l'aide d'une interface d'acquisition reliée à un ordinateur.

- Le circuit de commande de la sirène n'est pas relié au condensateur lors de cette expérience.

- L'acquisition commence lors de la fermeture de l'interrupteur K, le condensateur étant préalablement déchargé.

- La courbe obtenue est représentée ci-dessous.

a)- Reproduire le schéma du montage et indiquer les branchements de l'interface pour visualiser u_AB = f (t).

b)- Déterminer la valeur du temps caractéristique τ de ce circuit et vérifier que cette valeur est un accord avec les caractéristiques du circuit.

2. Déclenchement de l'alarme.

Ce circuit commande une sirène qui se déclenche dès que la tension aux bornes du condensateur atteint la valeur de 8,0 V.

a)- À l’aide de la courbe u_AB = f (t) donnée, déterminer la durée Δt dont dispose l'habitant pour quitter l'appartement et fermer la porte.

b)- Expliquer pourquoi le fait de fermer la porte empêche l'alarme de se déclencher.

2)- Correction.

1. Étude de la charge du condensateur dans le circuit RC.

a)- Schéma du montage et branchements de l'interface pour visualiser u_AB = f (t).

Schéma du montage et branchements de l'interface

- Les différentes valeurs : R = 47 kΩ ; C = 1,1 mF ; E = 9,0 V

b)- Valeur du temps caractéristique τ de ce circuit.

- Exploitation graphique :

- On utilise la relation suivante :

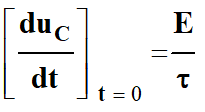- dérivée Comment démontrer cette relation ? : lien

- Pour déterminer graphiquement la valeur de τ, on trace la tangente à l’origine à la courbe u_AB = f (t).

- L’abscisse du point M d’intersection de la tangente avec l’asymptote horizontale donne la valeur de la constante de temps τ.

ZOOM

zoom

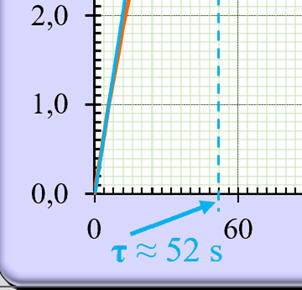
- Vérification : cette valeur est un accord avec les caractéristiques du circuit :

- L’association en série d’un condensateur de capacité C et d’un conducteur ohmique de résistance R constitue un dipôle RC.

- La durée de charge du condensateur d'un dipôle (R, C) dépend de la résistance R du conducteur ohmique et de la capacité C du condensateur.

- Temps caractéristique τ :

- τ = R . C.

- Application numérique :

- τ = 47 × 10³ × 1,1 × 10^–3

- τ ≈ 51,7 Ω

- τ ≈ 52 Ω

- Le résultat trouvé, avec l’exploitation de la tangente à l’origine et de la courbe, est en accord avec la valeur du temps caractéristique théorique.

► Autre méthode :

- Si on charge le condensateur pendant la durée Δt = τ , la tension aux bornes du condensateur est égale à 63 % de sa tension maximale U_max = E.

- Utau = 5,7 V

- Exploitation graphique :

- On trouve la même valeur pour la constante de temps τ.

- Cette méthode est plus précise que celle qui utilise le tracé de la tangente à l’origine.

- Pour plus de précision, il vaut mieux utiliser les deux méthodes simultanément.

2. Déclenchement de l'alarme.

a)- Durée Δt dont dispose l'habitant pour quitter l'appartement et fermer la porte.

- Exploitation de la courbe u_AB = f (t) :

- Ce circuit commande une sirène qui se déclenche dès que la tension aux bornes du condensateur atteint la valeur de 8,0 V.

- Exploitation graphique : par lecture graphique, on lit la date à laquelle la valeur de la tension aux bornes du condensateur C vaut u_AB = 8,0 V.

- Le résident dispose d’une durée d'environ Δt ≈ 1,1 × 10² s, c’est-à-dire 2 min environ.

b)- Explication : Pourquoi le fait de fermer la porte empêche l'alarme de se déclencher ?

- Le fait de fermer la porte court-circuite le condensateur. Le condensateur se décharge instantanément et la tension aux bornes du condensateur est nulle.

- Comme la tension aux bornes du condensateur u_AB < 8,0 V, la sirène ne se déclenche pas.