|
|
Mouvement dans un champ de gravitation Exercices |
|
|
|
|
|
Pour se promener dans le système solaire. |
|
QCM r
|
1)- Exercice 04 page 270 : Exploiter les coordonnées du vecteur accélération :
|
Exploiter les coordonnées du vecteur accélération :
Le centre de masse de Phobos, satellite naturel
de la planète Mars, est en mouvement circulaire autour de cette
planète. 1.
Déterminer les
coordonnées du vecteur accélération du centre de masse de Phobos
dans le repère de Frenet lié au référentiel « marsocentrique ». 2.
Montrer que le
mouvement de P est uniforme.
|
|
Exploiter les coordonnées du vecteur accélération : 1.
Coordonnées du vecteur accélération du
centre de masse de Phobos dans le repère de Frenet lié au
référentiel « marsocentrique ».
-
Schéma de la situation : Ou
-
Mars, corps à répartition sphérique
de masse, se comporte comme un objet ponctuel de masse
MM.
-
Phobos est l’objet qui subit
l’attraction de Mars.
-
Référentiel d’étude : Référentiel
marsocentrique considéré comme galiléen.
-
-
Comme le mouvement est circulaire, on
utilise le repère de Frenet associé au référentiel marsocentrique.
-
Repère de Frenet :
-
Phobos est soumis à la force de
gravitation exercée par Mars :
-
-
Expression de la force dans le repère
de Frenet :
-
-
Le champ de gravitation créé par la
Marsau point P de
l’espace :
-
-
En conséquence :
►
Caractéristiques du vecteur
accélération
-
On applique la deuxième loi de Newton au satellite
Phobos:
-
-
Phobos n’est soumis qu’à la force de
gravitation exercée par Mars (on néglige les autres actions mécaniques).
-
-
Le vecteur accélération
-
2.
Caractéristiques du mouvement de P :
-
Expression du vecteur accélération
dans le repère de Frenet
-
-
-
Avec :
-
-
Il découle de ceci que :
-
-
Le mouvement du satellite Phobos est
circulaire uniforme dans
le référentiel marsocentrique.
-
D’autre part :
-
-
On retrouve le fait que
v = cte, car G,
MM et
r sont des constantes.
►
Expression du vecteur vitesse
-
Le vecteur vitesse est tangent à la
trajectoire au point considéré :
-
|
2)- Exercice 06 page 270 : Déterminer les caractéristiques d’une vitesse :
|
Déterminer les caractéristiques d’une vitesse : Le télescope spatial Hubble a permis de nombreuses découvertes
dans le domaine de l’astrophysique. Il est placé sur une orbite quasiment circulaire à l’altitude
h = 600 km par rapport à la surface de la Terre. 1. Par application de la deuxième loi de Newton, déterminer les coordonnées du vecteur accélération du centre de masse H de Hubble dans le repère de Frenet lié au référentiel géocentrique. 2.
Déterminer les coordonnées du vecteur
vitesse de Hubble dans le repère de Frenet. 3.
Calculer la valeur de la vitesse de Hubble
dans le référentiel géocentrique.
-
Données :
-
Masse de la Terre :
MT = 5,97 × 1024 kg
-
Rayon de la Terre :
RT
= 6,37 × 103 km
-
G = 6,67 × 10–11
N . m2 . kg–2
-
HST
|
|
Déterminer les caractéristiques d’une vitesse :
La Terre est l’astre attracteur de masse MT La Terre est située à la distance
r
=
h +
RT
1. Coordonnées du vecteur accélération du centre de masse H de Hubble dans le repère de Frenet lié au
référentiel géocentrique.
-
Deuxième loi de Newton :
-
Énoncé.
-
Schéma de la situation :
-
Dans le cas présent, le télescope
Hubble, de masse m,
est soumis à l’attraction de
la Terre :
-
Force exercée par la Terre sur le satellite Hubble :
-
-
Dans le cas présent, la deuxième loi
de Newton permet d’écrire la relation suivante :
-
-
En utilisant le repère de Frenet lié
au référentiel géocentrique :
-
-
-
On en déduit les coordonnées du
vecteur accélération dans le repère de Frenet.
-
-
Avec :
r =
h +
RT
-
2.
Coordonnées du vecteur vitesse de Hubble
dans le repère de Frenet.
-
On connait les coordonnées du vecteur
accélération.
-
D’autre part :
-
-
Comme la composant tangentielle de
l’accélération est nulle :
-
-
Le mouvement du satellite Hubble est
circulaire uniforme dans le référentiel géocentrique.
-
En exploitant l’accélération
normale :
-
-
Le vecteur vitesse est tangent à la
trajectoire dans la position considérée :
-
3.
Valeur de la vitesse de Hubble dans le
référentiel géocentrique.
-
|
3)- Exercice 08 page 271 : Établir la troisième loi de Kepler :
|
Établir la troisième loi de Kepler : Europe est un satellite de Jupiter, de masse MJ.
Son orbite, de rayon r, est supposée circulaire. Sa vitesse a pour valeur : 1.
Établir l’expression de sa période de
révolution T. 2.
En déduire la valeur du rapport
3.
Énoncer la troisième loi de Kepler dans le
référentiel « jupiterocentrique ».
Données :
-
Masse de Jupiter :
MJ = 1,898 × 1027 kg
-
G = 6,67 × 10–11
N . m2 . kg–2
|
Établir la troisième loi de Kepler : 1.
Expression de sa période de révolution T.
-
Schéma de la situation :
-
La période
T de révolution du
satellite Europe est la durée qu’il met pour effectuer un tour
autour de Jupiter :
-
2.
Valeur du rapport
-
En élevant l'expression précédente au carré
et en ordonnant, on peut écrire :
-
-
La constante s’identifie à
- . -
Valeur de la constant k :
3.
Énoncé de la troisième loi de Kepler dans le
référentiel « jupiterocentinque ».
-
Le carré de la période de révolution
T des satellites de
Jupiter est proportionnel au cube du rayon
r de leur orbite supposée
circulaire.
-


![]() .
.



![]()
4)- Exercice 10 page 271 : Exploiter la troisième loi de Kepler :
|
Exploiter la troisième loi de Kepler : Les gros satellites de Jupiter, encore appelés satellites
galiléens, ont été découverts par Galilée. On donne les périodes de révolution T et le rayon
r de la
trajectoire quasi circulaire de deux de ces satellites :
1.
Énoncer la troisième loi de Kepler dans le
référentiel « jupiterocentrique ». 2.
Montrer que les données du tableau
confirment que ces deux satellites sont en orbite autour de Jupiter.
-
Données :
-
Masse de Jupiter : MJ
= 1,898 × 1027 kg
-
G = 6,67 × 10–11 N
. m2 . kg–2 |
Exploiter la troisième loi de Kepler : 1.
Troisième loi de Kepler dans le référentiel
« jupiterocentrique ».
-
Le carré de la période de révolution
T des satellites de Jupiter est proportionnel au cube du rayon r de leur orbite supposée circulaire.
-
2.
Les satellites sont en orbite autour de
Jupiter.
-
On va vérifier que :
-
-
Pour chaque satellite.
-
Pour le satellite Io :
-
-
Pour le satellite Ganymède :
-
-
En conséquence :
-
kIo ≈
kGa ≈ 4,17 ×
10–17 j2 . km–3
-
Valeur de la constant k dans
le cas de Jupiter :
-
-
kIo ≈
kGa ≈
k
-
Les satellites Io et Ganymède
orbitent bien autour de Jupiter.
-
Remarque :
-
Si on travaille avec les quatre
satellites Io, Europe, Ganymède et Callisto, on peut tracer la courbe :
-
T2 =
f (r3).
-
Exploitation avec le tableur Excel :
-
Tableau de valeurs :
Satellite
T
(jours)
r
(km)
T2
(j2)
r3
(km–3)
Io
1,77
4,22E+05
3,13
7,52E+16 Ganymède
7,15
1,07E+06
51,12
1,22E+18
Europe
3,55
6,71E+05
12,60
3,02E+17
Callisto
16,8
1,88E+06
282,24
6,64E+18
Droite de régression :
équation du type
T2
= a . r3 + b
a b
4,252E-17 -3,927E-01
Unité
(j2)
. (km–3)
(j2)
-
Graphe : étude statistique réalisée
avec Excel :
-
Les points sont sensiblement alignés.
-
Équation de la droite moyenne
obtenue :
-
T2 ≈ 4,25 × 10–17
× r3
-
Ce graphique est en accord avec la
troisième loi de Kepler.
-
Il montre que pour les satellites de
Jupiter :
-



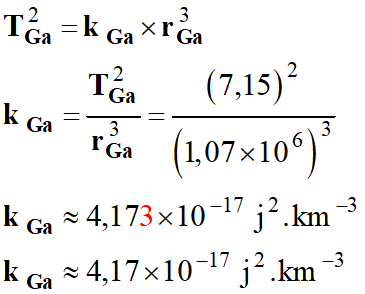


![]()
5)- Exercice 12 page 271 : Satellite CFOSAT :
|
Satellite CFOSAT : Le 29 octobre 2018, le satellite CFOSAT, de masse m, a été mis en orbite circulaire autour de la Terre à une altitude de h = 519 km par le
CNES et son homologue chinois le CNSA, pour cartographier les vents et les vagues à la surface
des océans.
1.
Schématiser la situation et représenter la
force de gravitation exercée par Terre sur le satellite. 2.
Montrer que le mouvement du centre de masse
C du satellite CFOSAT est uniforme dans le référentiel géocentrique.
4.
Déterminer la période de révolution T
du satellite.
-
Données :
-
Masse de la Terre : MT
= 6,0 × 1024 kg
-
Rayon de la Terre : RT
= 6,4 × 103 km
-
G = 6,67 × 10–11 N
. m2 . kg–2 |
|
Satellite CFOSAT : 1.
Schéma de la situation avec la force de
gravitation exercée par Terre sur le satellite.
-
Schéma de la situation à l’instant
t : 2.
Caractéristique du mouvement du centre de
masse C du satellite CFOSAT dans le référentiel géocentrique.
-
Référentiel d’étude : Référentiel
géocentrique considéré comme galiléen.
-
-
Comme le mouvement est circulaire, on
utilise le repère de Frenet associé au référentiel géocentrique.
-
Repère de Frenet :
-
Le satellite est soumis à la force de
gravitation exercée par la Terre :
-
-
Deuxième loi de Newton :
-
Énoncé.
-
Dans le cas présent, la deuxième loi
de Newton permet d’écrire la relation suivante :
-
-
Avec
r =
RT +
h
-
-
En utilisant le repère de Frenet lié
au référentiel géocentrique :
-
-
-
On en déduit les coordonnées du
vecteur accélération dans le repère de Frenet.
-
-
Coordonnées du vecteur vitesse du
satellite CFOSAT dans le repère de Frenet.
-
On connait les coordonnées du vecteur
accélération.
-
D’autre part :
-
-
Comme la composant tangentielle de
l’accélération est nulle :
-
-
Le mouvement du satellite CFOSAT est
circulaire uniforme dans le référentiel géocentrique. 3.
Caractéristiques du vecteur vitesse
-
En exploitant l’accélération
normale :
-
-
Le vecteur vitesse est tangent à la
trajectoire dans la position considérée et orienté dans le sens du
mouvement :
-
-
Schéma de la situation à l'instant
t : 4.
Période de révolution T du satellite.
-
La période T de révolution du
satellite est la durée qu’il met pour effectuer un tour autour de la
Terre :
-
-
Application numérique :
-
|
6)- Exercice 14 page 272 : Balance cosmique :
|
Balance cosmique : Le tableau ci-dessous donne la période de révolution de quelques planètes du système solaire, ainsi que le rayon de leur orbite assimilable à un cercle dans le
référentiel héliocentrique.
1.
Établir l’expression de la valeur de la
vitesse du centre de masse d’une de ces planètes dans le référentiel
héliocentrique. 2.
En déduire l’expression de sa période de
révolution en fonction de G, r et MS
(masse du Soleil). 3.
Donner l’expression du rapport
La troisième loi de Kepler
est-elle vérifiée ? 4.
Déterminer la masse MS du
Soleil. 5.
Justifier en quoi la troisième loi de Kepler
est une « balance cosmique ».
-
Données :
-
1an = 3,156 × 107 s
-
G = 6,67 × 10–11 N
. m2 . kg–2
|
|
Balance cosmique : 1.
Expression de la valeur de la vitesse du
centre de masse d’une de ces planètes dans le référentiel
héliocentrique.
-
On choisit la planète Mars :
-
Schéma de la situation :
-
Référentiel d’étude : Référentiel
héliocentrique considéré comme galiléen.
-
-
Comme le mouvement est circulaire, on
utilise le repère de Frenet associé au référentiel héliocentrique.
-
Repère de Frenet :
-
La planète Mars est soumise à la
force de gravitation exercée par le Soleil :
-
-
L’application de la deuxième loi de
Newton dans le référentiel héliocentrique supposé galiléen permet
d’écrire la relation suivante :
-
-
En utilisant le repère de Frenet lié
au référentiel héliocentrique :
-
-
-
On en déduit les coordonnées du
vecteur accélération de Mars dans le repère de Frenet.
-
-
Coordonnées du vecteur vitesse de
Mars dans le repère de Frenet.
-
On connait les coordonnées du vecteur
accélération.
-
D’autre part :
-
-
Comme la composant tangentielle de
l’accélération est nulle :
-
-
Le mouvement de Mars est circulaire
uniforme dans le référentiel héliocentrique.
-
En exploitant l’accélération
normale :
-
-
Pour Jupiter, on obtient la formule
suivante :
-
-
Et pour Saturne :
-
2.
Expression de sa période de révolution en
fonction de G, r et MS (masse du
Soleil).
-
La période T de révolution du
satellite Mars est la
durée qu’il met pour effectuer un tour autour du Soleil :
-
-
Relation pour Jupiter :
-
-
Relation pour Saturne :
-
3.
Expression du rapport
-
On élève chaque expression précédente
au carré et on ordonne :
-
-
Vérification de la troisième loi de
Kepler :
-
On calcule la valeur de
la constante k pour chaque planète :
-
En conséquence, à partir des
différentes mesures, on montre que :
-
-
On vérifie ainsi la troisième loi de
Kepler. 4.
Détermination la masse MS
du Soleil.
-
À partir de la relation :
-
-
5.
Troisième loi de Kepler et « balance
cosmique ». - À partir de la connaissance de la période T et du rayon r de l’orbite des satellites d’un Astre, on peut déterminer la valeur de la masse
M de l’astre attracteur
en utilisant la troisième loi de Kepler.
-
-
La troisième loi de Kepler joue le
rôle de « balance cosmique ».
-
Mesure de
G.
|
|
|