|
|
Mouvement dans un champ de gravitation
|
|
|
|
|
|
Exercices : énoncé et correction
Préparation à l'ECE : Vérification des lois de Kepler 1)- Exercice 04 page 270 : Exploiter les coordonnées du vecteur
accélération. 2)- Exercice 06 page 270 : Déterminer les caractéristiques d’une
vitesse. 3)- Exercice 08 page 271 : Établir la troisième loi de Kepler. 4)- Exercice 10 page 271 : Exploiter la troisième loi de Kepler. 5)- Exercice 12 page 271 : Satellite CFOSAT 6)- Exercice 14 page 272 : Balance cosmique. 7)- DS N° 01 Les Lunes de Saturne (60 min) : Exercice 20 page 274. 8)- Préparation à l’ECE : Vérification des lois de Kepler.
|
|
QCM r
|
I-
Le
mouvement des satellites et des planètes.
1)- Force et champ de gravitation.
►
La Loi de Gravitation universelle.
-
Loi de Newton : 1687
-
Énoncé :
-
Deux corps ponctuels
A et
B, de masses
mA
et mB,
séparés par une distance r,
exercent l’un sur l’autre des forces attractives.
-
Le corps
A exerce sur le
corps B la
force
-
![]()
-
Le corps
B exerce sur le
corps A la
force
-
![]()
-
Ces deux forces ont :
-
Même direction, la droite (AB),
-
Même valeur et des sens opposés.
-
Expression de la valeur :
-
![]()
-
Expression vectorielle :
-

-

-
Conséquence :
-
![]()
-
G
est appelé la constante de gravitation universelle :
-
G
≈ 6,67 × 10–11 m3
. kg–1 . s–2
ou m2 . kg–2
. N
-
Unités :
-
La force
F s’exprime en
newton (N) et les masses en kilogramme (kg).
-
Valeur des masses
m et
m’ en kg.
-
Distance séparant les deux masses
ponctuelles : r
en m
-
Les forces se représentent par des
flèches, appelées vecteurs, de même longueur, de même direction, mais de sens
opposés.
-
Autre expression (en utilisant le
vecteur unitaire)
![]() :
:
-

-

►
Application :
-
Calculer la valeur des forces
d’attraction Terre – Lune et Lune – Terre.
-
Faire un schéma.
-
Pourquoi une seule de ces actions est
perceptible ? Laquelle ?
►
Correction :
-
Dans le cas de l’interaction
gravitationnelle entre la Terre et la Lune, la valeur de la force exercée par la
Terre sur la Lune est donnée par l’expression :
-
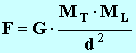
-
MT :
masse de la Terre : MT =
5,98 x 1024 kg.
-
ML :
masse de la Lune : ML =
7,34 x 1022 kg.
-
d :
distance entre le centre de la Terre et le centre de la Lune :
-
d
= 3,84 × 105 km.
-
Calculer la valeur de
F et représenter le
vecteur force F :
-
Échelle : 1 cm ↔ 1,00 ×
1020 N
-
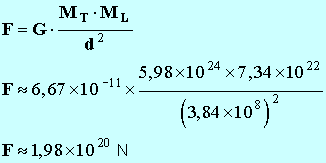
-
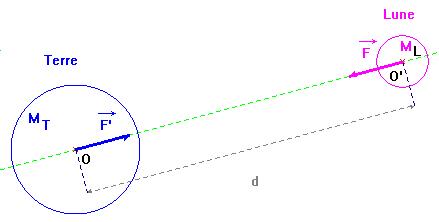
Schéma :
-
Cette force
F
retient la Lune sur son orbite autour de la Terre.
- Cette force due à l’interaction gravitationnelle est une force attractive représentée
par le vecteur
![]() , appliqué au centre de la Lune et dirigé vers le
centre de la Terre.
, appliqué au centre de la Lune et dirigé vers le
centre de la Terre.
►
Additif :
-
La portée de l’interaction
gravitationnelle est infinie mais diminue rapidement.
-
Elle est inversement
proportionnelle au carré de la distance.
- Comme elles sont toujours attractives, elles cumulent leurs effets et se manifestent
à des
distances astronomiques.
|
Corps
source de
champ |
Corps A
de masse mA |
|
Système placé
dans le champ |
Corps B
de
masse mB
situé à la distance d de
A |
|
Force subie par
le
système
placé
dans le champ
dû
au corps source |
|
|
Autre expression
vectorielle de la force |
|
|
Expression du
champ obtenue par
identification entre
les deux expressions
des forces |
|
|
Lignes de champ |
|
2)- Mouvement des satellites et des planètes.
a)-
Application : Satellite Artificiel de la Terre
à trajectoire circulaire
-
Schéma de la situation :
-
On étudie le mouvement
du centre de masse P d’un
satellite, de masse m,
en orbite circulaire autour de la Terre.
-
La Terre est l’astre
attracteur de masse MT.
-
La Terre, corps à
répartition sphérique de masse se comporte comme un objet ponctuel de masse
MT.
-
Le satellite est l’objet qui subit
l’attraction de la Terre.
-
Référentiel d’étude : Référentiel
géocentrique considéré comme galiléen.
-
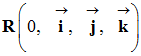
-
Comme le mouvement est circulaire, on
utilise le repère de Frenet associé au référentiel géocentrique.
-
Repère de Frenet : ![]()
-
Le satellite est soumis à la force de
gravitation exercée par la Terre :
-
![]()
-
Schéma :

Ou
-
Expression de la force dans le repère
de Frenet :
-

-
Le champ de gravitation
créé par la Terre au point P
de l’espace :
-
![]()
-
En conséquence :
![]()
►
Caractéristiques du vecteur
accélération
![]() du satellite :
du satellite :
-
On applique la deuxième loi de Newton
au satellite :
-
![]()
-
Le satellite n’est soumis qu’à la force
de gravitation exercée par la Terre.
-

-
Le vecteur accélération
![]() du satellite a
même direction, même sens et même valeur que le vecteur champ de gravitation
du satellite a
même direction, même sens et même valeur que le vecteur champ de gravitation
![]() .
.
![]() =
=
![]()
►
Caractéristiques du mouvement du
satellite :
-
Expression du vecteur accélération dans
le repère de Frenet
-
![]()
-
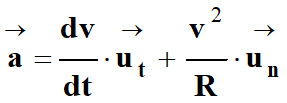
-
Avec :
-
![]()
-
Il découle de ceci que :
-
![]()
-
Le mouvement du satellite est
circulaire uniforme dans le référentiel géocentrique.
-
D’autre part :
-

-
On retrouve le fait que
v = cte, car
G, MT
et r sont des constantes.
►
Expression du vecteur vitesse
![]() du
satellite :
du
satellite :
-
Le vecteur vitesse est tangent à la
trajectoire au point considéré :
-



|
L’application de la
deuxième loi de Newton dans un repère de Frenet |
-
Pour Ptolémée (IIe
siècle), la Terre autour de laquelle tourne le Soleil est le centre du Monde.
-
Copernic est à l’origine du système
héliocentrique (1543).
-
Dans ce référentiel, les huit planètes
(2006) du système solaire ont des trajectoires quasi circulaires dont le centre
est le Soleil.
-
Kepler (1571 – 1630) utilisant les
travaux de son maître Tycho Brahe (1546 – 1601) formule les trois lois qui
décrivent le mouvement des planètes autour du Soleil.
2)- Première loi de Kepler : Loi des orbites.
|
|
-
Remarque : le cercle est une ellipse
dont les deux foyers sont confondus avec le centre.
-
Définition d’une ellipse :
-
Une ellipse est l’ensemble des points
dont la somme des distances à deux points fixes
F et
F’ (les foyers) est
une constante : r1
+ r2
=
-
Le grand axe de l’ellipse est égal à
-
La distance entre les deux foyers est 2
c.
-
Schéma :
3)- Deuxième loi de Kepler : Loi des aires.
|
balaie des aires égales pendant des
durées égales. |
-
Le segment de droite qui relie le
centre du Soleil au centre de la planète balaie des aires égales pendant des
durées égales.
-
Il résulte de ceci que la planète se
déplace plus vite lorsqu’elle se rapproche du Soleil.
-
En toute rigueur, le mouvement d’une
planète n’est pas uniforme.
4)- Troisième loi de Kepler : Loi des périodes.
|
et le carré de la période
T
de révolution est la même : |
-
Cette constante ne dépend pas de la
masse de la planète.
-
Si la trajectoire est un cercle de
rayon r, on
peut écrire que :![]()
-
Cette constante peut être calculée.
-
Exemple :
-
Dans le cas du système solaire, on peut
donner l’expression de la période de révolution d’une planète du système
solaire :
-
La période de révolution d’une planète
est la durée qu’elle met pour effectuer un tour autour du Soleil :
-

-
En élevant cette expression au carré et
en ordonnant, on peut écrire :
-

-
La constante s’identifie à 
-
En conséquence, on peut déterminer la
masse du Soleil à partir de la période de révolution
T et du rayon
r de
l’orbite d’une planète à trajectoire circulaire.
-
Mesure de la constante de gravitation
par Cavendish (1798)
-
Les trois lois de
Kepler, relatives aux planètes en orbite autour du Soleil, peuvent être
généralisées à tout satellite ou planète en orbite autour d’un astre de masse
M.
-
Elles permettent de prévoir les
caractéristiques de leur mouvement.
1)- Satellite géostationnaire.
|
-
Un Satellite
Géostationnaire est un satellite qui reste toujours à la verticale
d’un même point P de la Terre. -
Le plan de l’orbite dans le
référentiel géocentrique est le plan équatorial. -
Quelle est la période de
révolution T d’un tel satellite ? -
En déduire l’altitude h
d’un Satellite géostationnaire. -
Calculer la valeur de la
vitesse du satellite géostationnaire dans le référentiel
géocentrique. -
Données : -
1 j = 86164 s = 23 h 56 min
4 s -
G
= 6,67 × 10–11 m3 . kg–1 . s–2 -
MT
= 5,98 × 1024 kg -
RT
= 6400 km |
|
►
Les satellites
géostationnaires : -
« Ces satellites sont
positionnés à la verticale d’un point de l’équateur et sont
immobiles par rapport à la surface de la Terre ». -
Un satellite
géostationnaire est immobile dans un référentiel terrestre. -
C’est pour cette raison que
l’on peut pointer une antenne dans sa direction. -
Un satellite
géostationnaire est animé d’un mouvement circulaire dans le
référentiel géocentrique.
►
Période de révolution T
d’un Satellite Géostationnaire : -
Le satellite
géostationnaire met la même durée que celle mise par la Terre pour
effectuer un tour autour de l’axe des pôles -
C’est la durée pour
effectuer un tour dans le référentiel géocentrique : -
C’est la durée d’un jour
sidéral -
1 j = 86164 s = 23 h 56 min
4 s
►
Altitude de
révolution h d’un Satellite Géostationnaire : -
Schéma de la situation : 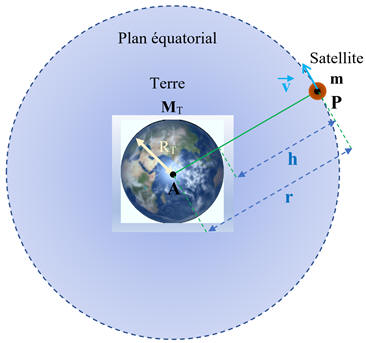
-
L’astre central est la
Terre de masse MT. -
r
= h + RT -
Expression de la période de
révolution T : -
-
-
Application numérique : -
►
Valeur de la vitesse du
satellite géostationnaire dans le référentiel géocentrique -
-
On peut utiliser le fait
que : -
|
|
QCM r
|
|
Exercices : 1)- Exercice 04 page 270 : Exploiter les coordonnées du vecteur
accélération. 2)- Exercice 06 page 270 : Déterminer les caractéristiques d’une
vitesse. 3)- Exercice 08 page 271 : Établir la troisième loi de Kepler. 4)- Exercice 10 page 271 : Exploiter la troisième loi de Kepler. 5)- Exercice 12 page 271 : Satellite CFOSAT 6)- Exercice 14 page 272 : Balance cosmique. 7)- DS N° 01 Les Lunes de Saturne (60 min) : Exercice 20 page 274. 8)- Préparation à l’ECE : Vérification des lois de Kepler.
|
|
|