|
Vérification des trois lois de Kepler :
PARTIE I : Vérification de la première
loi de Kepler
-
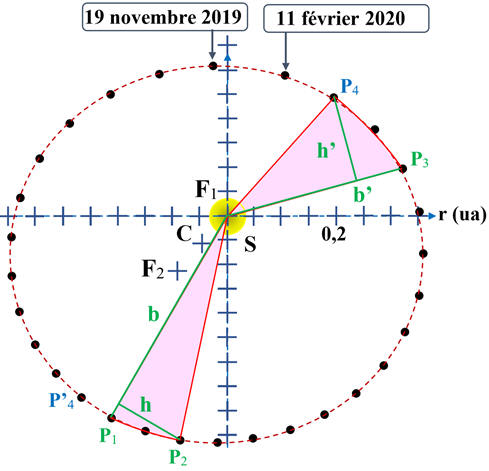
Caractéristiques de la trajectoire de
Mercure :
-
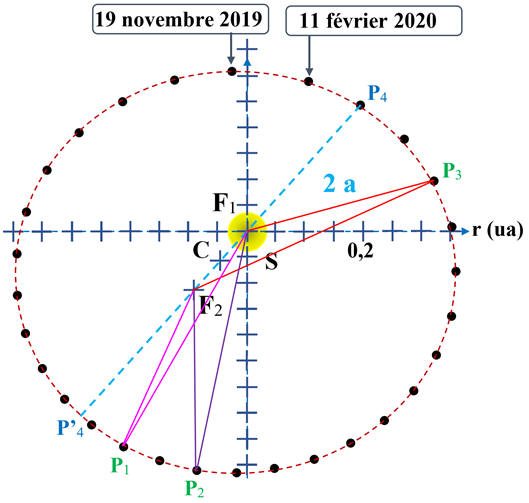
On remarque que le mouvement de Mercure
est quasi circulaire dans le référentiel héliocentrique.
-
Un cercle est une ellipse dont les deux
foyers F1 et F2 sont confondus.
-
Dans le cas présent, F1
et F2 sont très proches l’un de l’autre car la
trajectoire de mercure est quasi circulaire dans le référentiel héliocentrique
-
Le
centre de masse S du Soleil
est situé au foyer F1 de l’ellipse
-
F2 est le symétrique de
F1 par rapport au centre C du grand axe P4P’4.
-
On va vérifier sur la trajectoire de
mercure dans le référentiel héliocentrique que :
-
PiF1
+ PiF2 = 2 a
-
Pour pouvoir travailler avec les mesures
sur le schéma, on divise l’expression précédente par 2 a :
-
Il vient :
-
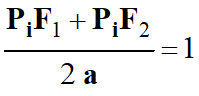
-
On vérifie la valeur de ce rapport pour
quelques positions choisies :
-
On va réaliser les mesures avec le
logiciel PhotoFiltre muni de
l’Outil
Mesures :
-
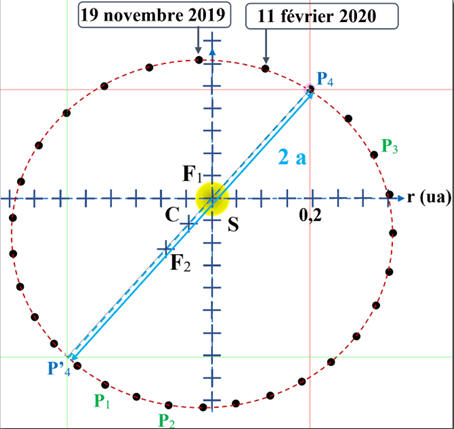
Mesure de la valeur de la longueur 2
a :
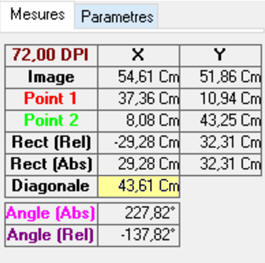
-
2 a ≈ 43,61 cm
-
Tableau de valeurs :
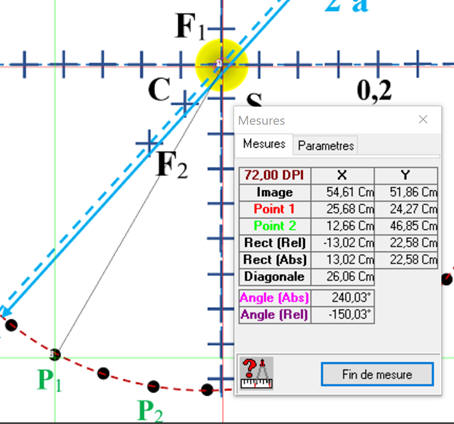
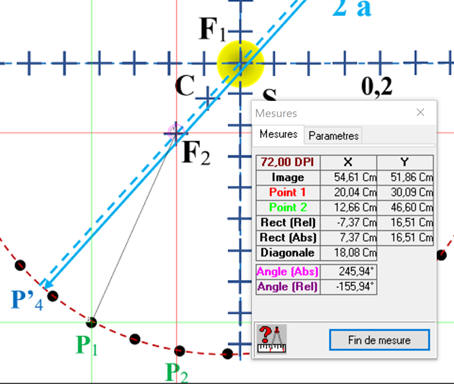
-
On réalise les autres mesures en
utilisant la même méthode :
|
2 a ≈ 43,61 cm
|
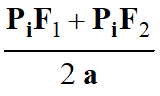
|
|
P1F1
(cm)
|
26,06
|

|
|
P1F2
(cm)
|
18,08
|
|
P2F1
(cm)
|
25.65
|
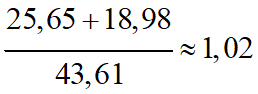
|
|
P2F2
(cm)
|
18,98
|
|
P3F1
(cm)
|
20,16
|
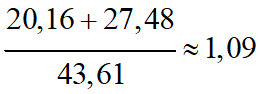
|
|
P3F2
(cm)
|
27,48
|
|
P4F1
(cm)
|
17,82
|

|
|
P4F2
(cm)
|
26,03
|
-
Aux erreurs de mesures près, la
trajectoire de Mercure dans le référentiel héliocentrique est quasiment une ellipse.
PARTIE II : Deuxième loi de Kepler
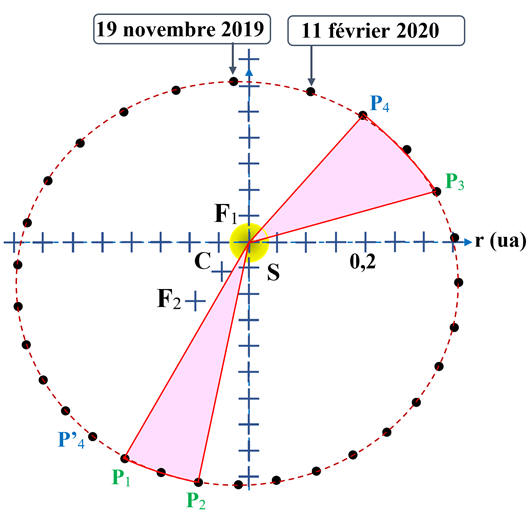
1.
Tracé des secteurs elliptiques SP1P2
puis SP3P4.
-
Schéma :
2.
Évaluation de l’aire des surfaces ainsi
délimitées.
-
On fait l’approximation suivante :
-
On assimile l’aire d’un secteur à celle
du triangle correspondant :
-
Pour le secteur elliptiques
F1P1P2
, on choisit le triangle F1P1P2.
-
Pour le secteur elliptiques
F1P3P4
, on choisit le triangle F1P3P4.
-
L’aire d’un triangle est donnée par la
formule suivante :
-
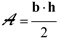
-
Mesures :
|
Triangle
F1P1P2
|
|
Triangle
F1P3P4
|
|
|
b
(cm)
|
26,06
|
b’
(cm)
|
20,16
|
|
h
(cm)
|
7,93
|
h’
(cm)
|
9,77
|
|
Aire
(cm2
× 102)
|
1,03
|
Aire
(cm2)
|
0,985
|
-
Aux erreurs de mesures près, on remarque
que la valeur de l’aire du triangle F1P1P2
est proche de celle du triangle F1P3P4.
3.
La deuxième loi de Kepler est vérifiée :
-
Les aires parcourues pendant des durées
égales (6 jours) sont quasiment égales
PARTIE III : Troisième loi de Kepler
1.
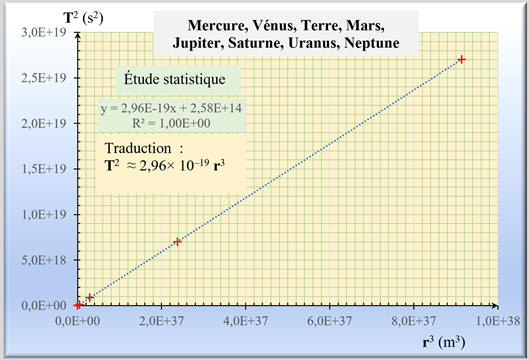
Exploitation du graphique :

-
La courbe représentative de la fonction
T2 =
f (r3) est une
droite passant pratiquement par l’origine.
-
Ce que confirme l’étude statistique :
-
On en déduit que :
T2 = k .
r3 pour les
planètes du système solaire.
-
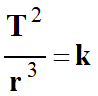 avec
k ≈ 3,01 × 10–19 s2
. m–3. avec
k ≈ 3,01 × 10–19 s2
. m–3.
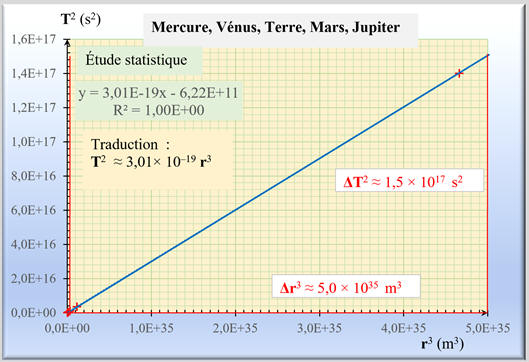
-
k
est le coefficient directeur de la droite moyenne tracée :
-
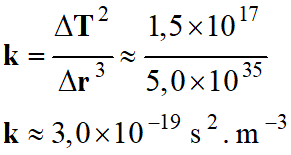
-
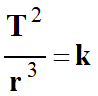
-
La troisième loi de Kepler est vérifiée.
-
Remarque :
-
Résultat pour les 8 planètes du système
solaire :
12
|
T
(jours)
|
r
(km)
|
T2
(s2)
|
r3
(m3)
|
|
Mercure
|
7,60E+06
|
5,79E+10
|
5,78E+13
|
1,942E+32
|
|
Vénus
|
1,94E+07
|
1,09E+11
|
3,77E+14
|
1,281E+33
|
|
Terre
|
3,16E+07
|
1,49E+11
|
9,96E+14
|
3,308E+33
|
|
Mars
|
5,94E+07
|
2,27E+11
|
3,52E+15
|
1,170E+34
|
|
Jupiter
|
3,74E+08
|
7,753E+11
|
1,40E+17
|
4,660E+35
|
|
Saturne
|
9,30E+08
|
1,429E+12
|
8,64E+17
|
2,918E+36
|
|
Uranus
|
2,65E+09
|
2,875E+12
|
7,03E+18
|
2,376E+37
|
|
Neptune
|
5,20E+09
|
4,504E+12
|
2,70E+19
|
9,137E+37
|
|
Droite de régression
:
Équation
du type T2 = a . r3
+ b
|
a
|
b
|
|
2,96E-19
|
2,581E+14
|
|
|
Unité
|
(j2)
. (km–3)
|
(j2)
|
-
Graphe :
-
On en déduit que :
T2 = k .
r3 pour les
planètes du système solaire.
-
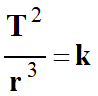 avec
k ≈ 2,96 × 10–19 s2
. m–3. avec
k ≈ 2,96 × 10–19 s2
. m–3.
-
Si on exprime
k avec deux chiffres significatifs :
-
k
≈ 3,0 × 10–19 s2 . m–3
2.
L’astéroïde Cérès :
-
Diamètre de l’astéroïde Cérès :
D =
950 km,
-
Période de révolution autour du Soleil
TC = 4,5 ans.
-
En utilisant la troisème loi de Kepler,
on peut déterminer la valeur du rayon
rC de l’orbite de l’astéroïde Cérès :
-
Comme l’astéroïde Cérès gravite autour du
Soleil :
-
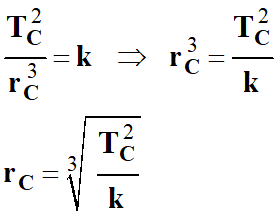
-
Application numérique :
-
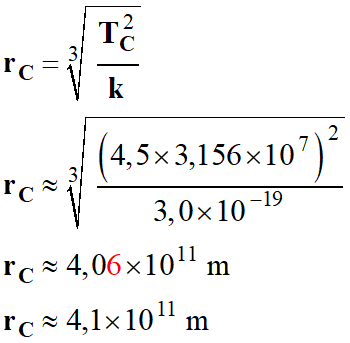
|