Chap. N° 12 Mouvement dans un champ uniforme

- Dans un champ de pesanteur uniforme, les forces de pesanteur s’exerçant sur un objet de masse m sont équivalentes à une force unique appelée poids .

image : champ de pesanteur

Interactions, Forces et Champs (Cours de première)

Champs et forces

3)- Champ électrique uniforme .

a)- Définition.

- Un champ électrique est dit uniforme dans une région de l’espace si le vecteur champ conserve en tout point de cette région, la même direction, le même sens et la même valeur.

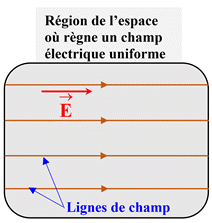
ligne de champ électrique

- Les lignes de champ sont des droites parallèles entre elles.

b)- Ligne de champ :

- Une ligne de champ vectoriel est une ligne tangente en chacun de ses points au vecteur champ.

- Elle est orientée par une flèche dans le même sens que celui du champ.

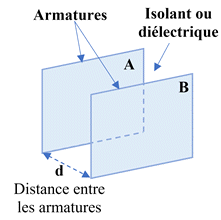
c)- Le condensateur plan :

- Un condensateur est formé de deux conducteurs métalliques appelés armatures, séparés par un isolant qui peut être de l'air ou un diélectrique.

- Le plus utilisé et le plus connu des condensateurs est le condensateur plan.

- Un condensateur plan est formé par deux plateaux conducteurs parallèles A et B appelés armatures, séparés par un isolant de faible épaisseur d.

condensateur plan

- Charge du condensateur :

- Pour charger un condensateur, on utilise un générateur de courant.

- Schéma :

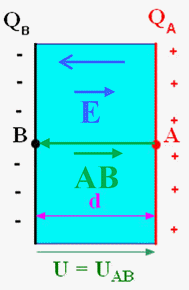
condensateur plan

- Caractéristiques du champ électrique entre les plaques :


Direction	Perpendiculaire aux plaques
Sens	De la plaque chargée positivement vers la plaque chargée négativement (sens des potentiels décroissants)
Valeur	; E ↑ si \|U\| ↑ et d ↓

- Relation :

- Valeur du champ :


E	Valeur du champ électrique ( V . m^–1)
U	Valeur de la tension U_AB (V)
d	Distance entre les armatures (m)

II- Le mouvement dans un champ uniforme.

1)- Cas du champ de pesanteur

a)- Introduction.

- Système étudié : S = {m, G)

- Référentiel d’étude : référentiel terrestre supposé galiléen

- Repère d’espaces lié au référentiel d’étude :

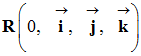
- Bilan des forces : on se place dans le cas où le système est uniquement soumis à son poids .

- Conditions initiales :

- Au temps t = 0 :

- Au temps t = 0 s, les coordonnées du point mobile G, centre de masse de la bille sont :

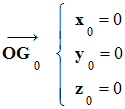
- position initiale

- Au temps t = 0, le vecteur vitesse du système est contenu dans le plan (Oxy)

- Le vecteur vitesse fait un angle α avec l’axe horizontal (Ox).

- vitesse initiale

- Schéma de la situation :

- Le champ de pesanteur :

- Est toujours verticale et orienté vers le bas.

- Coordonnées du vecteur :

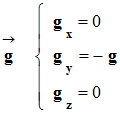
- vecteur g

- Deuxième loi de Newton :

Dans un référentiel galiléen, la somme des vecteurs forces

appliquées à un système S, de masse m et de centre de masse G,

est égal au produit de sa masse m par le vecteur accélération

de son centre de masse.

Valeur des forces F en newton (N)

Valeur de la masse m en kilogramme (kg)

Valeur de l’accélération a_G en mètre par

seconde au carré (m . s^–2)

- Dans le cas présent :

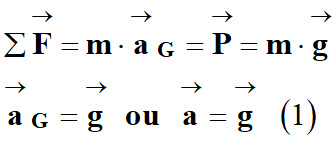
- Deuxième loi de Newton

b)- Détermination du vecteur accélération .

- Coordonnées du vecteur accélération :

vecteur a

vecteur g

On tire de

l’équation (1)

vecteur a

- Le vecteur accélération est vertical et orienté vers le bas.

c)- Détermination du vecteur vitesse.

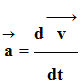
- vecteur a

- Le vecteur accélération est la dérivée par rapport au temps du vecteur vitesse .

- La détermination du vecteur vitesse nécessite de rechercher la primitive par rapport au temps de chaque coordonnée du vecteur accélération en tenant compte des conditions initiales.

- On cherche les primitives des équations précédentes.

- Il apparaît des constantes qui sont liées aux conditions initiales.

- Les constantes d’intégration apparues dans les primitives sont liées aux conditions initiales : c’est-à-dire les coordonnées du vecteur vitesse à l’instant initial.

vecteur v

D’après les

conditions initiales

vecteur v

- Au cours du mouvement du point mobile G, la coordonnée v_z = 0.

- Le mouvement du point G se fait dans le plan (Oxy) contenant le vecteur vitesse initiale .

- Ce plan est appelé, plan de tir.

d)- Détermination du vecteur position.

- On opère de la même façon :

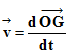
- vecteur v

- Le vecteur vitesse est la dérivée par rapport au temps du vecteur position .

- La détermination du vecteur position nécessite de rechercher la primitive par rapport au temps de chaque coordonnée du vecteur vitesse en tenant compte des conditions initiales.

vecteur OG

D’après les

conditions

initiales

vecteur OG

- Remarques :

- Le mouvement suivant l'axe x'Ox est rectiligne uniforme.

- Le mouvement suivant l'axe y'Oy est rectiligne uniformément varié.

- Le mouvement de G est contenu dans le plan (Oxy) appelé plan de tir.

- Il contient le vecteur .

e)- Détermination de la trajectoire.

- La trajectoire d’un point est l’ensemble des positions successives occupées par ce point au cours du temps.

- On élimine le temps t pour trouver la relation entre les coordonnées x et y du vecteur position.

- Comme le mouvement a lieu dans le plan (Oxy) :

- y = f (x).

vecteur OG

On en déduit l’équation de la trajectoire

équation de la trajectoire

- La trajectoire de G est une portion de parabole contenue dans un plan vertical contenant le vecteur vitesse .

chronophotographie

Vidéo 1

Vidéo 2

- Elle est liée aux conditions initiales.

- On peut limiter l’étude des mouvements dans un champ uniforme à une étude dans un repère à deux dimensions.

2)- Cas du champ électrique uniforme

a)- Introduction.

- Un électron M de masse m, porte la charge électrique q = – e.

- L’électron M pénètre, dans le vide, avec le vecteur vitesse , faisant un angle α avec l’horizontale à l'intérieur d'un condensateur plan.

- L’électron M coïncide avec O à la date t = 0 s.

- Système S : électron M de masse m et de charge q

- Référentiel terrestre supposé galiléen

- Le repère d’espace choisi : contient le vecteur vitesse et le vecteur .

- Référentiel d’étude : référentiel terrestre supposé galiléen

- Repère d’espaces lié au référentiel d’étude :

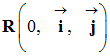
- Conditions initiales :

- Position et vitesse du mobile au temps t = 0 s

vecteur OM0

vecteur v0

- Schéma de la situation :

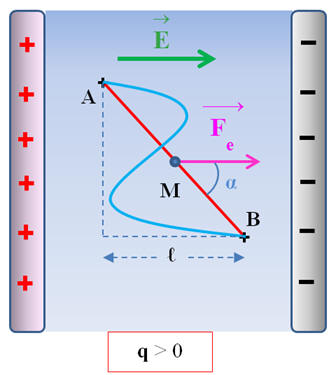
- Données :

- Masse : m = 9,1 × 10^–31 kg ; Charge : q = – e = – 1,6 × 10^–19 C

- E = 4,7 × 10³ V / m ; g = 9,81 N . kg^–1

- Bilan des forces : Inventaire des forces extérieures exercées sur l’électron.

- Son poids .

- La force électrostatique

- L’électron se déplace dans le vide, il n’y a pas d’interaction avec l’air.

- Comparaison de F_e et P.

- F_e = e . E ≈ 1,6 × 10^–19 × 4,7 × 10³

- F_e ≈ 7,5 × 10^–19 N

- P = m . g ≈ 9,1 × 10^–31 × 9,81

- P ≈ 8,9 × 10^–30 N

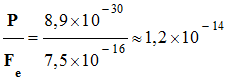
- P / Fe = 1,2 E-14

- En conséquence, P << F_e, on peut négliger les effets du poids devant celui de la force électrostatique F_e.

- En conséquence, l’électron n’est soumis qu’à la force électrostatique .

- Coordonnées des différentes forces et vecteurs dans le repère choisi :

vecteur E

force électrique

- Application de la deuxième loi de Newton :

- Dans le cas présent :

- D’où :

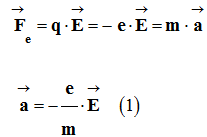
- deuxième loi de Newton

b)- Détermination du vecteur accélération.

- On peut donner les coordonnées du vecteur accélération dans le repère d’étude :

vecteur a

force électrique

l’équation

(1),

on tire

vecteur a

- Ainsi par recherche des primitives, on retrouve les coordonnées du vecteur vitesse et du vecteur position.

c)- Détermination du vecteur vitesse.

vecteur v

D’après

les

conditions

initiales

vecteur v

d)- Détermination du vecteur position.

vecteur OM

D’après

les

conditions

initiales

vecteur OM

e)- Détermination de la trajectoire.

- Équation de la trajectoire :

- On élimine le temps t entre x et y pour exprimer y = f (x).

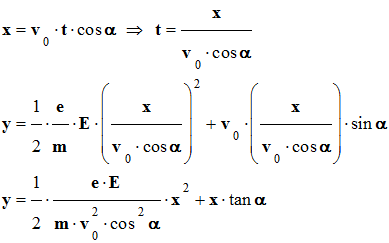
- Équation de la trajectoire

- La trajectoire de l’électron est une portion de parabole.

- Déviation d’un faisceau d’électrons (oscilloscope)

III- Aspects énergétiques.

1)- Forces conservatives.

- Une force est conservative si le travail de cette force est indépendant du chemin suivi, c’est-à-dire s’il ne dépend que des positions du point de départ A et du point d’arrivée B.

Travail et énergie

- Le poids est une force conservative.

- De même la force électrique est une force conservative.

schéma

- Lors du mouvement d’un système dans un champ de pesanteur ou électrique uniforme, en l’absence de forces non conservatives, l’énergie mécanique du système se conserve.

- Son énergie cinétique est totalement convertie en énergie potentielle, et inversement.

- Le théorème de l’énergie cinétique permet de calculer des valeurs de vitesse ou la coordonnée verticale du système selon les données disponibles.

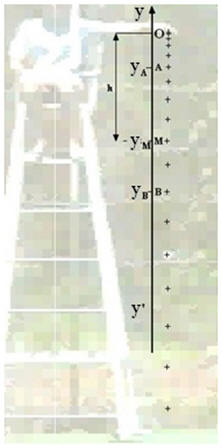
2)- Exemple : Cas de la chute libre.

Expérience :

- On filme, à l’aide d’une WebCam, la chute d’une balle de golf de masse m = 44 g.

chute libre : chronophotographie

- Tableau de valeurs et pointages :

- On réalise les pointages à l’aide du logiciel AVIMECA 2.7.

chronophotographie

Pointages AviMéca
t	x	y	v
s	m	m	m / s
0	-4,80E-03	4,80E-03	0,000
0,04	0,00E+00	4,80E-03	0,000
0,08	0,00E+00	4,80E-03	0,060
0,12	0,00E+00	0,00E+00	0,480
0,16	4,80E-03	-3,36E-02	0,900
0,2	4,80E-03	-7,20E-02	1,21
0,24	0,00E+00	-1,30E-01	1,63
0,28	4,80E-03	-2,02E-01	2,10
0,32	0,00E+00	-2,98E-01	2,45
0,36	-4,80E-03	-3,98E-01	2,88
0,4	-4,80E-03	-5,28E-01	3,25
0,44	-9,60E-03	-6,58E-01	3,66
0,48	-9,60E-03	-8,21E-01	4,14
0,52	-9,60E-03	-9,89E-01	4,36
0,56	-4,80E-03	-1,17E+00	4,76
0,6	-4,80E-03	-1,37E+00	5,13
0,64	-4,80E-03	-1,58E+00	5,63
0,68	-4,80E-03	-1,82E+00	6,13
0,72	-4,80E-03	-2,07E+00	6,38
0,76	-9,60E-03	-2,33E+00

- Les propriétés du clip sont les suivantes :

propriétés du clip

- Pour connaître la valeur de la vitesse à chaque instant à l’aide du tableur, on calcule la vitesse moyenne pendant un intervalle de temps très court (ici 80 ms) encadrant l’instant considéré :

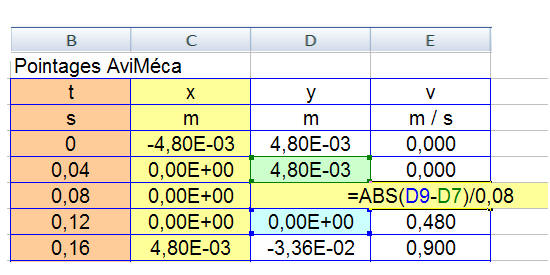
tableur

- On utilise la colonne E pour l’étude de la vitesse da bille.

- On prend modèle sur les autres colonnes pour la mise en forme.

- La vitesse initiale (au temps t = 0 s) : on lâche la balle sans vitesse initiale : la vitesse initiale est nulle.

- Pour calculer la valeur de la vitesse du point N° 2, on utilise la méthode déjà utilisée :

- On calcule la vitesse moyenne pendant un intervalle de temps très court encadrant l’instant considéré :

- On tape la formule suivante dans la cellule E8 : = ABS (D9 – D7) / 0,08

- Le signe égale : pour signifier à Excel que l’on tape une formule

- ABS () car on calcule la valeur de la vitesse qui est une grandeur positive

- L’intervalle de temps vaut : 2 t = 80 ms.

- On recopie cette formule vers le bas autant que nécessaire avec la souris (copier – glisser)

- On représente sur un même graphe, les variations de l’énergie cinétique, de l’énergie potentielle et le l’énergie mécanique en fonction du temps.

- On choisit comme origine de l’énergie potentielle la position initiale de la balle.

- Tableau de valeurs :

t	x	y	v	E_C	E_P	E_m
s	m	m	m	J	J	J
0	-4,80E-03	4,80E-03	0,00	0,00	0,00	0,00
0,04	0,00E+00	4,80E-03	0,00	0,00	0,00	0,00
0,08	0,00E+00	4,80E-03	0,06	0,00	0,00	0,00
0,12	0,00E+00	0,00E+00	0,48	0,01	0,00	0,01
0,16	4,80E-03	-3,36E-02	0,90	0,02	-0,01	0,00
0,2	4,80E-03	-7,20E-02	1,21	0,03	-0,03	0,00
0,24	0,00E+00	-1,30E-01	1,63	0,06	-0,06	0,00
0,28	4,80E-03	-2,02E-01	2,10	0,10	-0,09	0,01
0,32	0,00E+00	-2,98E-01	2,45	0,13	-0,13	0,00
0,36	-4,80E-03	-3,98E-01	2,88	0,18	-0,17	0,01
0,4	-4,80E-03	-5,28E-01	3,25	0,23	-0,23	0,00
0,44	-9,60E-03	-6,58E-01	3,66	0,30	-0,28	0,01
0,48	-9,60E-03	-8,21E-01	4,14	0,38	-0,35	0,02
0,52	-9,60E-03	-9,89E-01	4,36	0,42	-0,43	-0,01
0,56	-4,80E-03	-1,17E+00	4,76	0,50	-0,51	-0,01
0,6	-4,80E-03	-1,37E+00	5,13	0,58	-0,59	-0,01
0,64	-4,80E-03	-1,58E+00	5,63	0,70	-0,68	0,01
0,68	-4,80E-03	-1,82E+00	6,13	0,83	-0,79	0,04
0,72	-4,80E-03	-2,07E+00	6,38	0,89	-0,89	0,00
0,76	-9,60E-03	-2,33E+00

- Graphe 1 : E = f (t)

- Remarque :

- L’énergie cinétique augmente au cours du temps, l’énergie potentielle diminue au cours du temps, alors que l’énergie mécanique se conserve au cours du temps.

- Conclusion :

- Le système S, au cours de la chute, est soumis à son poids .

- Les forces de frottements sont négligeables dans les conditions de l’expérience (balle de petite dimension et hauteur de chute de faible dimension)

- L’énergie mécanique d’un système S soumis à des forces conservatives est constante, elle se conserve.

- Au cours du mouvement, la variation de l’énergie mécanique : ΔE_m = 0

- ΔE_C + ΔE_P = 0 => ΔE_C = – ΔE_P

- Lorsqu’il y a conservation de l’énergie mécanique, il y a transfert total de l’énergie potentielle en énergie cinétique.

3)- Principe de fonctionnement d’un accélérateur linéaire de particules.

Le canon à électrons :

- Un canon à électrons est constitué d’un filament qui, lorsqu’il est porté à haute température,

émet des électrons de vitesse initiale négligeable.

- Ces électrons sont ensuite accélérés à l’intérieur d’un condensateur plan dont les armatures A et B sont verticales

et entre lesquelles règne un champ électrostatique uniforme de valeur E.

- Schéma :

- On néglige le poids de l’électron devant la force électrostatique.

Le référentiel est supposé galiléen.

1)- Déterminer l’expression du travail de la force électrostatique entre les positions A et B (voir schéma).

2)- Montrer, en appliquant le théorème de l’énergie cinétique, que l’expression

de la valeur de la vitesse en B est :

- Calculer la valeur de v_B.

3)- Accélération et vitesse : une autre méthode

a)- Déterminer les coordonnées du vecteur accélération et du vecteur vitesse de l’électron au cours du mouvement entre les plaques A et B.

On choisira le repère indiqué sur le schéma.

b)- En déduire l’expression de la valeur de sa vitesse à chaque instant.

4)- Établir les équations horaires de son mouvement.

5)- Expression et valeur de la vitesse :

a)- Montrer que l’expression de la vitesse de l’électron lorsqu’il parvient à la plaque B du condensateur est :

b)- Calculer la valeur v_B de cette vitesse.

- Données :

- e = 1,60 × 10^–19 C ; m_e = 9,11 × 10^–31 kg ;

- AB = d = 3,00 cm ; E = 6,00 × 10⁴ V . m^–1.

Le canon à électrons :

- Étude préliminaire :

- On néglige le poids de l’électron devant la force électrostatique.

- Le référentiel est supposé galiléen :

- La force électrostatique :

- Dans le cas d’un électron : q = – e

- Les vecteurs et ont la même direction mais des sens opposés.

- Signe et valeur de la tension U_AB :

- est orienté de la plaque chargée positivement vers la plaque chargée négativement (sens des potentiels décroissants) :

- U_BA > 0 => U_AB < 0

- UAB = - 1,80 E3 V

1)- Expression du travail de la force électrostatique entre les positions A et B.

- travail de la force électrostatique

- Comme la tension U_BA > 0, le travail de la force électrostatique est moteur.

2)- Montrer, en appliquant le théorème de l’énergie cinétique, que l’expression

de la valeur de la vitesse en B est :

Aspects énergétiques des phénomènes mécaniques (cours de première)

La variation de l’énergie cinétique d’un système S en mouvement,

d’une position A à une position B, est égale à la somme des travaux

de toutes les forces appliquées au système S entre A et B :

variation de l’énergie cinétique

- Les unités :

ΔE_CA→B	Variation de l’énergie cinétique en joule (J)
E_CA et E_CB	Énergie cinétique en joule (J)
m	La masse en kilogramme (kg)
v	La vitesse en mètre par seconde (m . s^–1)
	Travail de la force en joule (J)
F	Valeur de la force en newton (N)
AB	Longueur du déplacement en mètre (m)
cos α	α angle (rad ou °) entre les vecteurs et cos α : sans unité