I- Des forces dans l’Univers.

1)- Forces de gravitation.

a)-  La Loi de Gravitation universelle.

-  Loi de Newton : 1687

-  Énoncé :

-  Deux corps ponctuels A et B, de masses m_A et m_B, séparés par une distance r, exercent l’un sur l’autre des forces attractives.

-  Le corps A exerce sur le corps B la force

-   

-  Le corps B exerce sur le corps A la force

-   

-  Ces deux forces ont : même direction :

-  La droite (AB), même valeur et des sens opposés.

-  Expression de la valeur :

-   

-  Expression vectorielle :

-   

-   

-  Conséquence :

-   

-  G est appelé la constante de gravitation universelle :

-  G ≈ 6,67 × 10^–11 m³ . kg^–1 . s^–2 ou m² . kg^–2 . N

-  Unités :

-  La force F s’exprime en newton (N) et les masses en kilogramme (kg).

-  Valeur des masses m et m’ en kg.

-  Distance séparant les deux masses ponctuelles : r en m

-  Les forces se représentent par des flèches, appelées vecteurs, de même longueur, de même direction, mais de sens opposés.

-  Expression vectorielle (en utilisant le vecteur unitaire ) :

-   

- 

b)-  Cas des corps célestes.

-  Ce résultat se généralise à des corps à répartition sphérique de masse.

-  La masse est répartie de façon régulière autour du centre du corps.

-  C’est le cas de la Terre, de la Lune, des planètes et des étoiles.

►  Application :

-  Calculer la valeur des forces d’attraction Terre – Lune et Lune – Terre.

-  Faire un schéma.

-  Pourquoi une seule de ces actions est perceptible ? Laquelle ?

►  Correction :

-  Dans le cas de l’interaction gravitationnelle entre la Terre et la Lune, la valeur de la force exercée par la Terre sur la Lune est donnée par l’expression :

-   

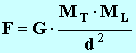
-  M_T : masse de la Terre : M_T  = 5,98 × 10²⁴ kg.

-  M_L : masse de la Lune : M_L  = 7,34 × 10²² kg.

-  d : distance entre le centre de la Terre et le centre de la Lune :

-  d = 3,84 × 10⁵ km.

-  Calculer la valeur de F et représenter le vecteur force F :

-  Échelle : 1 cm ↔ 1,00 × 10²⁰ N

-   

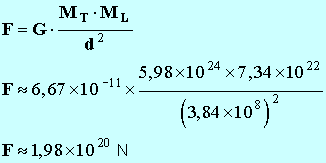
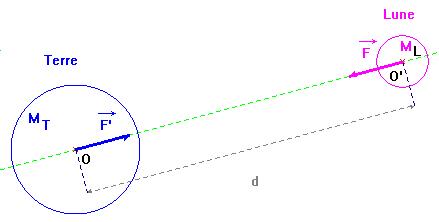
-  Schéma :

-  Cette force F retient la Lune sur son orbite autour de la Terre.

-  Cette force due à l’interaction gravitationnelle est une force attractive représentée par le vecteur , appliqué au centre de masse de la Lune et dirigé vers le centre de la Terre.

-  Additif :

-  La portée de l’interaction gravitationnelle est infinie mais diminue rapidement.

-  Elle est inversement proportionnelle au carré de la distance.

 -  Comme elles sont toujours attractives, elles cumulent leurs effets et se manifestent à des distances astronomiques.

2)- Force électrostatique.

a)-  Expérience 1 :

  Frotter une règle plastique sur de la laine.

  L’approcher de petits morceaux de papier posés sur la table.

-  La règle frottée attire des petits morceaux de papier.

-  Au cours de cette expérience, on a mis en évidence un phénomène d’interaction à distance entre deux corps.

-  Certains objets peuvent être électrisés par frottement.

-  Ils attirent alors à distance certains objets légers.

-  Les objets doivent être légers pour que le phénomène soit observable.

-  Un corps électrisé est un corps qui porte des charges électriques.

-  Un corps peut être électrisé par frottement, par influence et par contact.

b)-  Électrisation par frottement :

-  La règle frottée attire des petits morceaux de papier.

-  L’électrisation par frottement résulte d’un transfert d’électrons d’un corps vers un autre.

-  Par frottement, on agit sur la surface de la matière.

-  On n’agit pas au niveau du noyau.

-  L’électrisation par frottement résulte d’un transfert d’électrons d’un corps vers un autre.

-  Un corps chargé positivement possède un défaut d’électrons.

-  Un corps chargé négativement possède un excès d’électrons.

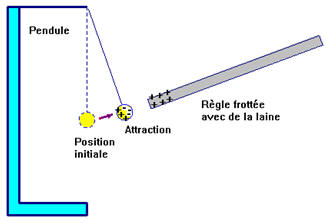
c)-  Électrisation par influence :

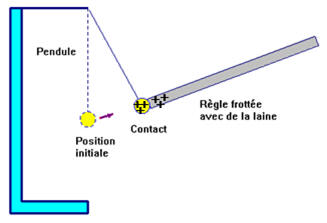
-  Lorsque l’on approche la règle frottée du pendule, la règle est électrisée par frottement alors que le pendule est électriquement neutre.

-  Avant contact, le pendule est électrisé par influence.

-  Le pendule est neutre avant contact, mais il est attiré.

-  Les électrons des atomes qui constituent le pendule sont attirés.

-  Des charges de signes contraires s’attirent.

-  Ils sont sous l’influence des charges positives de la règle.

-  Il se crée une dissymétrie dans la répartition des électrons permettant une attraction.

-  Globalement, le pendule reste neutre.

-  La zone en regard de la règle présente un excès d’électrons alors que la zone la plus éloignée de la règle présente un défaut d’électrons.

-  L’électrisation par influence résulte de la dissymétrie de la répartition des électrons dans un corps lorsqu’il subit l’influence d’un corps chargé.

d)-  Électrisation par contact :

-  Lors du contact entre le pendule électriquement neutre et la règle frottée chargée positivement, le pendule s’électrise.

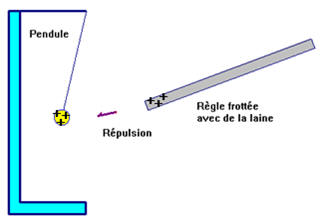
-  Puis, le pendule est repoussé, il porte une charge électrique de même signe que la règle frottée.

-  Des électrons du pendule passent sur la tige.

-  Le pendule se charge alors positivement, il présente un défaut d’électrons.

e)-  Conclusions :

-  Les corps chargés sont en interaction sous l’effet de leurs charges électriques :

-  C’est l’interaction électrostatique.

-  Elle peut être attractive ou répulsive.

f)-  Loi de Coulomb.

-  Charles Augustin Coulomb : 1785.

-  Caractéristiques des deux forces :

-  La force   est appliquée en B et la force  est appliquée en A.

-  Elles ont la même direction : la droite (AB).

-  Elles ont des sens opposés.

-  Elles sont attractives si les charges sont de signes opposés.

-  Elles sont répulsives si les charges sont de même signe.

-  Elles ont la même valeur :

-  Expression :

-   

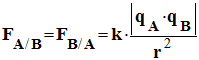
-  La constante k = 9,0 × 10⁹  N . m ² . C^–2. 

-  Au niveau de la première, on écrit :

-  k = 9,0 × 10⁹  S.I

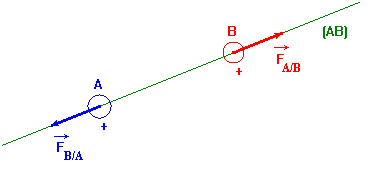
-  Considérons deux boules A et B chargées d’électricité positive.

-  La boule A agit sur la boule B par l’intermédiaire d’une force notée :

-   

-  Réciproquement la boule B agit sur la boule A par l’intermédiaire d’une force notée :

-   

-  Caractéristiques de chacune des forces :

-    et  

-  Premier cas : on considère que : q_A . q_B > 0

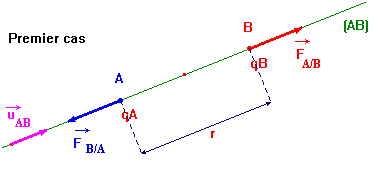
-  Deuxième cas : on considère que : q_A . q_B < 0

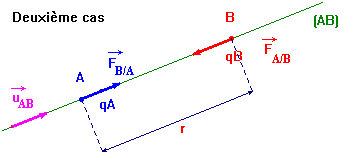
-  La Constante k :

-   

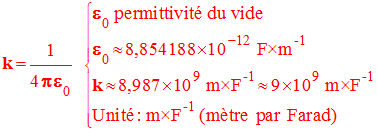
-  Au niveau de la première : k = 9,0 × 10⁹  S.I.

3)- Comparaison avec l’interaction gravitationnelle.

-  La force de gravitation est toujours attractive

-  La force électrostatique est attractive lorsque les deux charges en interactions sont de signes contraires.

-  Dans le cas où les deux charges sont de même signe, elle est répulsive.

-  La forces de gravitation et la force électrostatique sont toutes deux dirigées selon une droite qui joint le centre des deux corps en interaction.

-  Leur valeur est proportionnelle aux masses ou aux charges des corps en interaction.

-  Leur valeur est inversement proportionnelle au carré de la distance entre les masses ou les charges.

►  Application :

-  Dans l’atome d’hydrogène, comparer les valeurs des forces gravitationnelle et électrique s’exerçant entre le noyau et l’électron. Conclure.

-  On donne :

-  masse du proton : m_P = 1,67 × 10^–27  kg :

-  masse de l’électron : m_e = 9,11 × 10^–31  kg :

-  Charge élémentaire : e = 1,6 × 10^–19  C :

-  Constante de gravitation : G = 6,67 × 10^–11 S.I

-  Constante k : k = 9,0 × 10 ⁹  S.I.

-  Distance moyenne entre le noyau et l’électron : d ≈ 53 pm. 

-  Solution :

-  Expression de la force gravitationnelle :

-   

-  Valeur :

-  F_g ≈ 3,6 × 10^–47 N 

-  Expression de la force électrique :

-   

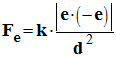
-  Valeur :

-  F_e ≈ 8,2 x 10^–8 N

-  Comparaison : on fait le rapport des deux forces :

-   

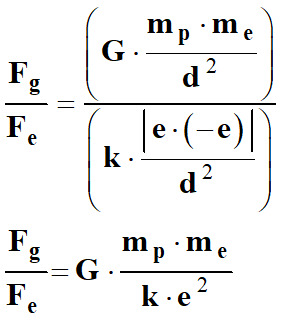
-  Application numérique :

-   

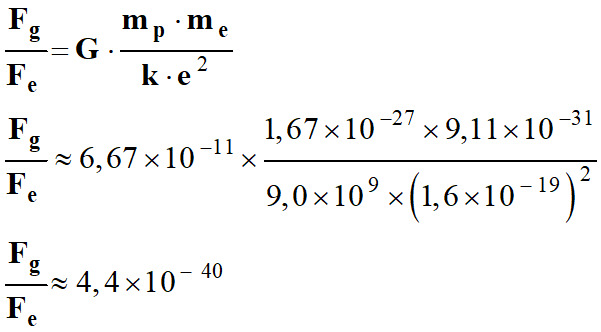
-  Conclusion : au niveau atomique, la force de gravitation est négligeable devant la force électrique.

II- La notion de champ en physique.

1)- Définitions :

-  Un champ scalaire est défini par une valeur associée à une unité en chaque point de l’espace considéré.

-  Un champ vectoriel est défini par un vecteur (direction, sens, valeur et unité) en chaque point.

  De façon générale, un champ est une grandeur physique (scalaire ou vectorielle) associée à chaque point de l’espace considéré.

►  Cartographie d’un champ.

  Pour cartographier un champ, on détermine les caractéristiques de ce champ en certains points de l’espace et on en donne une représentation.

-  Le nombre de points choisis est lié à la précision du champ que l’on veut représenter.

-  Dans le cas d’une cartographie des températures, on peut donner la température d’une région, ou donner la température par ville.

-  Cartographie des températures : chaque station météo donne la température du lieu sous abri.

-  Dans le cas d’un champ vectoriel, on peut définir les lignes de champ.

►  Ligne de champ :

  Une ligne de champ vectoriel est une ligne tangente en chacun de ses points au vecteur champ.

-  Elle est orientée par une flèche dans le même sens que celui du champ.

2)- Champs de gravitation et champ électrostatique.

a)-  Champ de gravitation :

b)-  Champ électrostatique :

III- Applications.

1)- Champ électrique uniforme : le condensateur plan.

a)-  Définition.

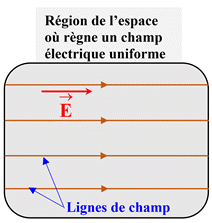
-  Un champ électrique est dit uniforme dans une région de l’espace si le vecteur champ  conserve en tout point de cette région, la même direction, le même sens et la même valeur.

-  Schéma :

-  Les lignes de champ sont des droites parallèles entre elles.

b)-  Le condensateur plan.

►  Description.

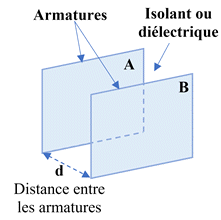
-  Un condensateur plan est formé par deux plateaux conducteurs parallèles A et B appelés armatures, séparés par un isolant de faible épaisseur d.

-  Schéma :

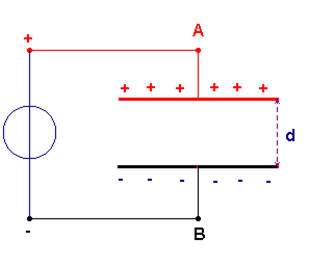
►  Charge du condensateur :

-  Pour charger un condensateur, on utilise un générateur de courant.

-  Schéma :

-  Le générateur transfère les électrons d’une armature sur l’autre.

-  On dit que le condensateur est chargé.

-  Le courant ne circule que lors de la charge.

-  Lorsque le condensateur est chargé, le courant ne circule plus.

-  L’armature reliée à la borne plus du générateur porte la charge + Q > 0 : + Q = Q_A

-  L’armature reliée à la borne plus du générateur porte la charge – Q < 0 : - Q = Q_B

-  Entre les armatures existe la tension U_AB = V_A – V_B > 0

-  Q, grandeur positive, est appelée charge du condensateur.

-  C’est la charge portée par l’armature positive du condensateur : + Q = Q_A = – Q_B

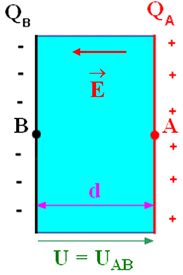
-  Dans l’espace situé entre les armatures, le champ électrique  :

-  Est considéré comme uniforme,

-  Sa direction est perpendiculaire aux armatures,

-  Son sens est dirigé de l’armature positive à l’armature négative (sens des potentiels décroissants),

-  Son intensité (sa valeur) :

-   

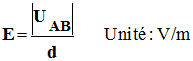
►  Pour aller plus loin :

-  Un champ électrique agit sur des particules chargées qu’elles soient immobiles ou en mouvement.

-  Un champ électrique permet de dévier ou d’accélérer un faisceau d’électrons.

►  Le canon à électrons.

-  C'est un dispositif qui accélère les électrons.

-  Il comprend :

-  Une plaque C appelée cathode (elle émet des électrons en utilisant l'effet thermoélectronique :

-  le filament f chauffe la cathode pour émettre des électrons.

-  Une plaque A appelée anode qui attire et accélère les électrons.

-  Elle est percée d'un trou pour laisser passer les électrons.

-  La tension U_AC peut atteindre quelques dizaines de kilovolts.

-  Le champ entre les deux plaques est uniforme et il est orienté de A vers C.

►  Les plaques de déviation.

-  Les électrons pénètrent avec une vitesse horizontale  à l'intérieur d'un condensateur plan dans lequel règne le vide.

-  Entre les deux plaques horizontales A et B de ce condensateur, séparées par la distance d, est appliquée une tension U_AB.

-  On admet que le champ électrique qui en résulte agit sur les électrons sur une distance L mesurée à partir de O.

-  Les électrons sont déviés vers le haut ou vers le bas suivant le signe de la tension U_AB.

Animation CabriJava

-    Application : écran d’oscilloscope. étude de l'oscilloscope ; Tensions variables et oscilloscope

-    Cours : Mouvement d’une particule chargée dans un champ électrique uniforme.

2)- Champs de pesanteur et de gravitation.

a)-  Champ de pesanteur.

-  Au voisinage de la Terre, un objet de masse m, situé au point A, est soumis à son poids .

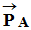-  De même l’objet de masse m, situé au point B, est soumis à son poids .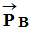

-  Ceci provient du fait que la Terre de masse M_T, crée dans son espace environnant un champ de pesanteur.

-  et

-  Schéma :

-  Le champ de pesanteur est un champ vectoriel.

-  La relation qui lie le champ de pesanteur  au point A et le poids d’un objet de masse m placé en ce point A est :

-   

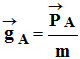
-  Caractéristiques de  :

	Origine :	Point A
	La direction ;	Verticale passant par le point A
	Le sens	Vers la Terre
	L’intensité ou la valeur
	Unités :	P en newton (N) m en kilogramme (kg) g en N / kg

►  Champ de pesanteur uniforme :

-  Lorsque les dimensions sont de l’ordre du kilomètre, on peut considérer que le champ de pesanteur est uniforme.

-  Sa valeur diminue d’environ 0,3 % si on s’élève de 10 km et sa direction varie d’environ 1° entre deux points distants de 100 km.

-  Caractéristiques du champ local  :

-  Schéma :

b)-  Champ de gravitation.

-  Une masse M crée un champ de gravitation  dans tout l’espace environnant.

-  Ce champ est mis en évidence grâce à l’interaction gravitationnelle qui existe entre la masse M, placée au point O de l’espace et la masse m, placée au point P de l’espace

-  (Mesure de G par Cavendish ).

Expérience de Cavendish

-  La masse m, située au point P de l’espace, subit une force

-  Le champ de gravitation est un champ vectoriel.

-  La relation qui lie le champ de gravitation en un point P de l’espace et la force d’attraction gravitationnelle qui s’exerce sur l’objet de masse m situé au point P de l’espace est :

-   

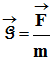
-  Schéma :

-  Expression et valeur de la force  :

-   

-  Caractéristiques de  :

c)-  Champ de gravitation et de pesanteur.

-  À cause du mouvement de rotation de la Terre, le poids d’un objet, de masse m, n’est pas tout à fait identique à la force d’attraction gravitationnelle exercée par la Terre sur cet objet.

-  On toute rigueur, en un même point P de l’espace :

-  Mais la différence entre et est faible.

-  Lorsque la précision le permet, on identifie localement le champ de pesanteur 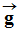 au champ de gravitation de la Terre .

-  Au voisinage de la Terre :

►  Application :

-  Calculer G_Terre à la surface de la Terre :

-  Comparer cette valeur à la valeur de g = 9,81 N . kg^–1 à Paris.

-  Données :

-  M_T = 5,98 × 10²⁴ kg ; R_T = 6400 km ; G = 6,67 × 10^–11 S.I

-   Valeur de G_Terre à la surface de la Terre :

-   

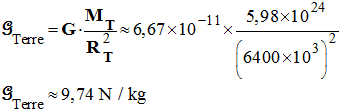
-  Incertitude relative :

-   

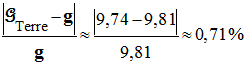
-  L’écart est faible.

►  Remarque

-  La Terre est légèrement aplatie aux pôles :

-  Rayon équatorial : R_T = 6380 km, valeur de G_Terre ≈ 9,80 N . kg^–1

-  Rayon polaire : R_T = 6360 km, valeur de G_Terre ≈ 9,86 N . kg^–1

   Conclusion :

-  Au voisinage de la Terre, le champ de pesanteur s’identifie au champ de gravitation si on néglige l’effet de la rotation de la Terre autour de l’axe des pôles.

3)- QCM.

  QCM Réalisé avec Questy 

Pour s'auto-évaluer

  Sous forme de tableau 

4)- Exercices.