TP physique N° 12, Mouvement le projectiles, énoncé, terminale S, tstp12ph

TP Physique N ° 12

Mouvements de projectiles :

en relation avec Phys. N° 10.

Enoncé.

Correction

I - Mouvement d'un projectile dans un champ de pesanteur.

II - Exploitation des résultats.

III - Exploitation du document 1.

IV - Application .

Correction

Programme 2012 :

Physique et Chimie

Programme 2020 :

Physique et Chimie

Matériel :

différentes balles – un ordinateur muni d’un tableur –

une Webcam –

les logiciels : Virtualdub – aviméca 2.7 – Excel.

Parabil Parabil.zip

I- Mouvement d’un projectile dans le champ de pesanteur.

1)- Protocole expérimental.

- Une bille est lancée avec la main avec une vitesse faisant un angle α avec le plan horizontal.

- Une étude chronophotographique permet d’étudier le mouvement de la bille dans un référentiel terrestre.

- La Webcam est située dans un plan perpendiculaire à l’axe de visée.

- Ouvrir le logiciel d’acquisition et de traitement vidéo : aviméca 2.7.

- Cliquer sur l’icône : et dans le dossier vidéo, choisir le fichier Parabil. Parabil.zip

- Choisir comme échelle de la vidéo : 200 % pour plus de précision.

- Repérer les différentes positions de la bille au cours de son mouvement.

Cliquer sur mesures.

Repérer les différentes positions de

la bille au cours de son mouvement.

À l’aide de la cible, repérer la position de la balle

et faire un clic gauche sur la première image.

Automatiquement, le logiciel affiche la deuxième image

de la vidéo et laisse une marque.

Repérer les positions successives occupées

par la balle au cours du temps.

- Cliquer sur l’icône Étalonnages :

Choisir l’origine des axes :

choisir comme origine des axes le centre de la balle

pour la position 10 ( position pour laquelle la balle est la plus haute)

Sélectionner, Échelles identiques.

Placer le premier point à l’origine des espaces (position 10)

et le deuxième point à la position 22 de la balle (dernière image).

Puis entrer la valeur : 1,49 m.

2)- traitement des résultats.

Cliquer sur l’icône :

Il apparaît l’affichage

ci-contre :

- Cliquer sur OK. Les valeurs sont dans le presse papier. Il ne reste plus qu’à les exploiter.

- Le logiciel : EXCEL.

- Ouvrir un fichier Excel

- Sélectionner coller .

- On obtient l’affichage suivant :

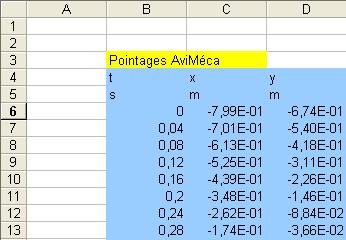
II- Exploitation des résultats.

1)- Étude de x = f (t) et y = g (t).

- À l’aide du logiciel étudier les variations des coordonnées du centre d’inertie G en fonction du temps.

- En déduire x = f (t) et y = g (t).

- Déterminer l’équation de la trajectoire y = h (x).

2)- Étude de v_x = f’ (t) et v_y = g’ (t).

- À l’aide du logiciel étudier les variations des coordonnées du vecteur vitesse du centre d’inertie G en fonction du temps.

- En déduire v_x = f’ (t) et v_y = g’ (t).

- Quelles sont les remarques que l’on peut faire ?

3)- Étude de a_x = f’’ (t) et a_y = g’’ (t).

- À l’aide du logiciel étudier les variations des coordonnées du vecteur accélération du centre d’inertie G en fonction du temps.

- En déduire a_x = f’’ (t) et a_y = g’’ (t).

- Quelles sont les remarques que l’on peut faire ?

4)- Récapitulatif.

- Faire un récapitulatif des différents résultats. Retrouver les conditions initiales du mouvement.

- Quelles sont les caractéristiques de . Donner la valeur de l’angle α.

- Commenter les différents résultats. Quelles sont les conclusions que l’on peut tirer ?

- Quels sont les facteurs qui interviennent dans le mouvement d’un projectile ?

III- Exploitation du document 1.

1)- Tracé du vecteur accélération.

- Tracer le vecteur accélération du centre d’inertie pour les positions G₅ et G₁₆.

2)- Exploitation.

- Que peut-on dire du vecteur accélération du centre d’inertie du mobile au cours du mouvement ?

- Quelles sont les caractéristiques du vecteur accélération au cours du mouvement ?

IV- Application.

Une balle de tennis de masse m est lancée d'un point O avec une vitesse initiale faisant un angle α avec l'horizontale.

On considère que la balle est en chute libre.

Données : v ₀ =12 m / s ; α = 60 ° ; m = 50 g et g = 9,81 m / s².

On choisit comme repère : y'Oy axe vertical orienté vers le haut et x'Ox axe horizontal orienté de gauche à droite.

Le plan (x'x, y'y) contient le vecteur vitesse . z'Oz est orthogonal au plan (x'x, y'y).

Les vecteurs forment un trièdre direct.

On choisit comme origine des espaces le point O et l'origine des dates l'instant ou la balle occupe la position O.

1)- Donner les équations horaires du mouvement. Que peut-on dire du mouvement de G suivant l'axe x'Ox, suivant l'axe y'Oy.

Dans quel plan s'effectue le mouvement de G ?

2)- Déterminer l'équation de la trajectoire du point G. Conclusion.

3)- Déterminer la portée horizontale (distance OC : les points O et C sont situés sur la même horizontale).

Donner l'expression littérale puis la valeur numérique.

4)- Quelle doit être la valeur de l'angle α pour que la portée horizontale soit maximale ?

5)- Déterminer la flèche c'est-à-dire l'altitude maximale atteinte par le projectile.

Donner l'expression littérale puis la valeur numérique.

6)- Recommencer les calculs pour α = 30 ° et tirer les conclusions.

Correction