Correction

Correction succincte

 Objectifs : résoudre une équation différentielle par la méthode d’Euler.

I- Chute d’une bille dans l'huile.

 1)- Protocole expérimental.

-  On filme, à l’aide d’une Webcam la chute d’une bille dans l’huile contenue dans une éprouvette graduée de 1 L.

-  On obtient le fichier : bille50.

-  Ouvrir le logiciel d’acquisition et de traitement vidéo :

aviméca 2.7. (Présentation avec Tour Operator)

-  Clique sur l’icône :  et dans le dossier vidéo, choisir le fichier : bille50.

-  Avant d’effectuer les mesures, cliquer sur l’icône  et choisir 200 % pour agrandir l’image et améliorer la précision.

-  Cliquer sur l’icône :  propriétés du clip et les noter.

-  Cliquer sur l’icône étalonnage :

-  Remarque : Ne pas oublier de choisir l’origine des axes. On peut choisir l’origine des axes après avoir effectué les mesures.

2)- traitement des résultats.

-  Cliquer sur l’icône : . Il apparaît l’affichage suivant :

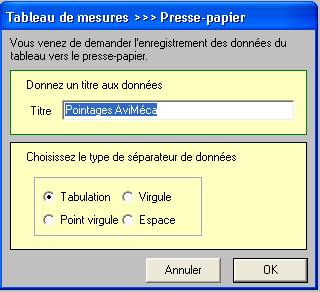
-  Cliquer sur OK. Les valeurs sont dans le presse papier. Il ne reste plus qu’à les exploiter.

-  Le logiciel : EXCEL.

-  Ouvrir le fichier : méthode_euler_eleves.xls

-  Sélectionner la cellule jaune et coller. On obtient l’affichage suivant :

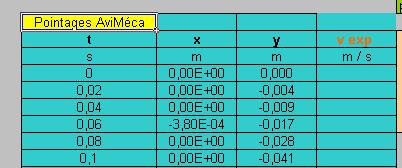
-  À l’aide du logiciel :

-  Déterminer la valeur de la vitesse à chaque instant et la valeur de la vitesse limite v_lim.

-  Cette valeur est très importante pour la suite.

-  Tracer v (t).

-  Commenter la courbe obtenue.

II- Exploitation des résultats.

1)- Modélisation.

-  La force de frottement exercée par un fluide peut-être modélisée de deux façons :

-  Modèle 1 : f = k₁.v

-  Modèle 2 : f = k₂.v ²

-  À partir de la deuxième loi de Newton, établir l’équation différentielle liant l’accélération a à la vitesse v et la mettre sous la forme :

-    avec

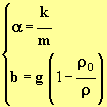
2)- méthode d’Euler.

-  Résoudre cette équation différentielle par la méthode d’Euler à l’aide du tableur Excel à l’aide des deux modèles de la force de frottement et la valeur de la vitesse limite v_lim.

-  Tracer pour chaque modèle v(t) et comparer les courbes obtenues avec celle obtenue expérimentalement.

-  Conclure quant à la validité du modèle pour la force de frottement hydrodynamique.

-  Que se passe-t-il si la valeur du pas δt augmente ou diminue ? Quelle est la valeur du pas la mieux adaptée à l’expérience ?

-  Explication de la méthode :

-  On se propose de résoudre numériquement l’équation différentielle (2) par la méthode d’Euler. 

-  Cette méthode consiste à obtenir des valeurs approchées de la fonction v = f (t) et d’en déduire une représentation graphique.

-  À condition de choisir δt suffisamment petit, on peut écrire que :

-  Or δv représente la variation de la valeur de la vitesse pendant la durée δt.

-  Si on connaît les valeurs de α et b et les conditions initiales, on peut trouver de proche en proche les différentes valeurs de la vitesse v au cours du temps.

-  Pour le modèle 1 : la relation devient :

-  Les conditions initiales sont les suivantes : au temps t₀ = 0, v = v₀.

-  On choisit une valeur de dt suffisamment petite : C’est le pas du calcul.

-  À la date t₁ =  t₀ +  δt,  la vitesse est devenue : v₁ =  v₀ +  δv₀ avec

-  

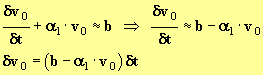
-  en conséquence :  ou

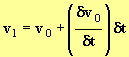
-  Cette valeur est calculable puisque les valeurs α₁, b et v₀ sont connues.

-  On procède de la même façon pour le calcul de v ₂.

-  À la date t₂ =  t₁ +  δt,  la vitesse est devenue : v₂ =  v₁ +  δv₁ = v₁ + (b –  α₁.v₁).δt.

-  À la date t_n+1 =  t_n +  δt,  la vitesse est devenue : v_n+1 =  v_n +  δv_n = v_n + (b -  α₁.v_n).δt.

-  On peut en répétant ce calcul, déterminer la valeur de la vitesse aux différentes dates séparées de δt. 

-  On peut ainsi obtenir la représentation graphique de v en fonction du temps t.

-  L’équation différentielle « a été résolue » numériquement par une méthode itérative.

-  Pour le modèle 2 : la relation devient :

-  Les conditions initiales sont les suivantes : au temps t₀ =  0, v = v₀.

-  On choisit une valeur de δt suffisamment petite : C’est le pas du calcul.

-  À la date t₁ =  t₀ +  δt,  la vitesse est devenue : v₁ =  v₀ +  δv₀ avec

-  

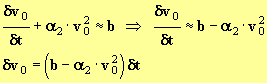
-  Cette valeur est calculable puisque les valeurs α₂, b et v₀ sont connues.

-  On procède de la même façon pour le calcul de v ₂.

-  À la date t₂ =  t  +  δt,  la vitesse est devenue : v₂ =  v₁ +  δv₁ = v₁ + (b –  α₂.v²₁).δt.

-  À la date t_n+1 =  t_n +  δt,  la vitesse est devenue : v_n+1 =  v_n +  δv_n = v_n + (b –  α₂.v ² _n).δt.

-  On peut en répétant ce calcul, déterminer la valeur de la vitesse aux différentes dates séparées de δt. 

-  On peut ainsi obtenir la représentation graphique de v en fonction du temps t.

-  L’équation différentielle « a été résolue » numériquement par une méthode itérative.

-  Remarque :

-  On peut améliorer la précision des calculs en choisissant un pas de calcul δt  plus petit, mais cela impose un grand nombre de calculs. 

-  Il faut disposer d’une calculatrice graphique ou d’un tableur

3)- Modèle 1 : Calcul des constantes α₁ et b.

-     et 

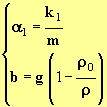
-  La connaissance des différentes masses volumiques permet de calculer la valeur de b.

-  à partir de la valeur de la vitesse limite, on peut calculer la valeur de a₁.

-  Lorsque le mobile a atteint sa vitesse limite :

- 

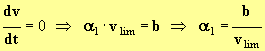
4)- Modèle 2 : Calcul des constantes a ₂ et b.

-     et 

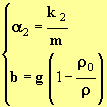
-  Pour b, la valeur est la même :

-  à partir de la valeur de la vitesse limite, on peut calculer la valeur de a₂.

-  Lorsque le mobile a atteint sa vitesse limite :

-   

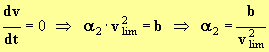
5)- exploitation avec Excel.

-  Entrer les valeurs des différentes constantes dans les cellules.

-  Méthode 1 :

-  On utilise le fait que : 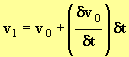 avec  et que :  

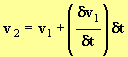
-  La colonne E permet de calculer les différentes vitesses et la colonne D permet de calculer la variation de la valeur de la vitesse pendant l’intervalle dt.

-  Dans la cellule E15, entrer la valeur de v₀ = 0

-  Dans la cellule D15 entrer la formule : = $H$12 – $I$12 * E15 puis dupliquer cette formule vers le bas.

-  Dans la cellule E16 entrer la formule : =E15+D15*$H$9 puis dupliquer vers le bas.

-  Méthode 2 :

-  On utilise le fait que : 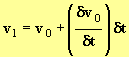 avec  et que :

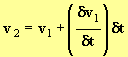
-  Dans la cellule G15, entrer la valeur de v₀ = 0

-  Dans la cellule F15 entrer la formule : = $H$12 – $J$12 * G15^2 puis dupliquer cette formule vers le bas.

-  Dans la cellule G16 entrer la formule : =G15 + F15*$H$9 puis dupliquer vers le bas.

III- Conclusions.