Exercices :  énoncé avec correction a)-  Exercice 7 page 180. Justifier la polarité d’un solvant. b)-  Exercice 9 page 180. Identifier un solvant polaire ou apolaire. c)-  Exercice 10 page 180. Expliquer la dissolution d’un solide ionique dans l’eau. d)-  Exercice 11 page 180. Écrire des équations de dissolution. e)-  Exercice 12 page 180. Étudier des solutions ioniques. f)-   Exercice 13 page 180. Expliquer la dissolution de l’acétone dans l’éther. g)-  Exercice 19 page 181. Concentrations molaires effectives. h)-  Exercice 22 page 182. Un médicament contre l’anémie.

I- Dissolution d’une espèce chimique.

1)- Introduction.

►    Solution électrolytique :

-    Une solution électrolytique est une solution qui conduit le courant électrique car elle contient des cations et anions.

-    Une solution électrolytique est électriquement neutre.

-  Elle contient autant de charges positives que de charges négatives.

►    Exemples de solutions électrolytiques :

-    Dissolution du permanganate de potassium dans l’eau.

-  On obtient une solution aqueuse colorée (violette) qui contient des ions permanganate et des ions sodium.

-    Dissolution de chlorure de sodium dans l’eau.

-  On obtient une solution aqueuse salée (incolore) qui contient des ions chlorure et des ions sodium.

►    Solution qui ne conduit pas le courant électrique :

-    Dissolution du saccharose (C₁₂H₂₂O₁₁) dans l’eau.

-  On obtient une solution sucrée qui est une solution aqueuse qui contient des molécules de saccharose.

-    Dissolution du diiode (I₂) dans l’eau :

-  On obtient une solution colorée qui est une solution aqueuse qui contient des molécules de diiode.

-    Ces solutions ne conduisent pas le courant électrique.

-    Lors de la réalisation de la solution, le soluté ne réagit pas avec l’eau.

-  C’est le cas de la solution de saccharose (C₁₂H₂₂O₁₁) et de celle du diiode (I₂).

-    La solution de saccharose contient des molécules de saccharose parmi des molécules d’eau et la solution de diiode contient des molécules de diiode parmi des molécules d’eau.

2)- Les différents types de solvants.

a)-  Les solvants polaires.

    Un solvant constitué de molécules polaires est un solvant polaire.

-    Exemple :

-    L’eau H₂O est un solvant polaire.

-  La molécule d’eau est une molécule polaire.

-    La liaison H – O est une liaison polarisée.

-  Ceci provient du fait que la molécule d’eau est une molécule coudée.

-  (Chap. N° 06 Cohésion de la matière à l’état solide)

 

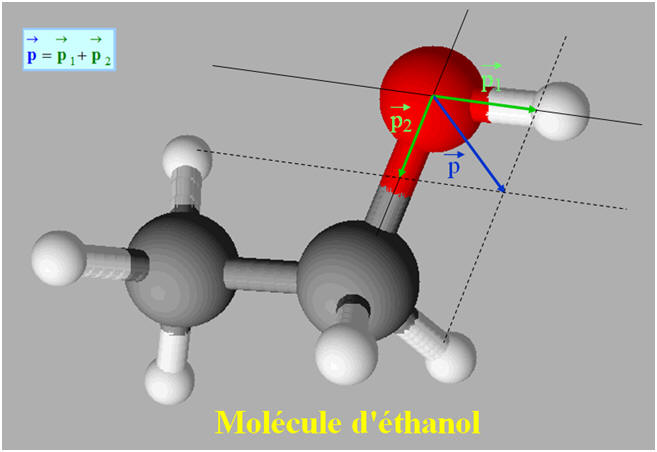
-    La molécule d’éthanol CH₃ – CH₂ – OH est une molécule polaire, c’est un solvant polaire.

-    Cette molécule possède des liaisons polarisée : C – O et H – O.

-    p (C – O) ≈ 1,3 D et p (H – O) ≈ 1,5 D

-    Par construction géométrique, on trouve : p (CH₃CH₂OH) ≈ 1,7 D

-    Géométrie de la molécule :

-    Échelle : 2 cm ↔ 1 D

-    ℓ_p1 ≈ 3 cm ; ℓ_p1 ≈ 2,6 cm 

-    On mesure ℓ_p ≈ 3,4 cm 

-    En conséquence, p (CH₃CH₂OH) ≈ 1,7 D

 

b)-  Les solvants apolaires.

    Un solvant constitué de molécules apolaires est un solvant apolaire.

-    Exemples : les molécules de cyclohexane, d’heptane, d’octane, … sont des molécules apolaires.

-    Cela vient du fait que la liaison C – H est faiblement polarisée.

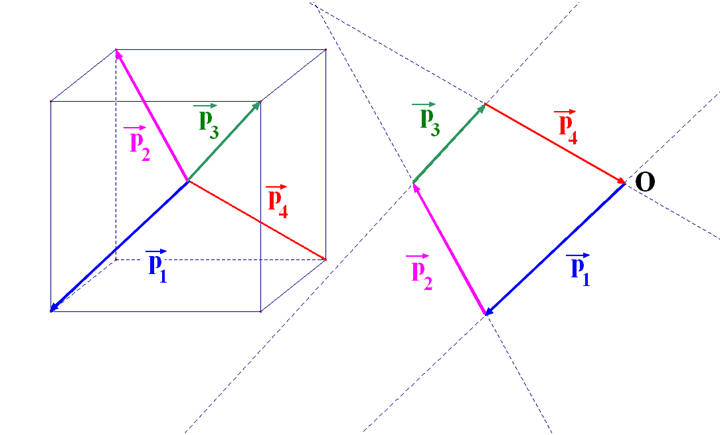
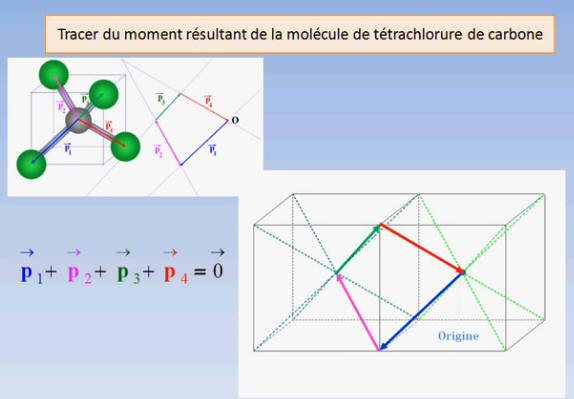
-    La molécule de tétrachlorure de carbone est apolaire bien que la liaison C – Cl soit polarisée.

-     Cette particularité est liée à la géométrie de la molécule.

 

-    L’atome de carbone est au centre d’un tétraèdre régulier dont les atomes de chlore occupent les sommets.

-    La somme vectorielle de tous les moments dipolaires est nulle.

 

 

Pour comprendre la construction dans l’espace

 

 

 

clip vidéo

Construction 

-    Remarque : On peut admettre, comme les liaisons C – H sont très peu polarisées que :

-    Les solvants dont les molécules ne comportent que des atomes de carbone et d’hydrogène sont apolaires.

-    Ceci , même en l’absence de symétrie de la molécule,

 

II- Dissolution d’un solide ionique dans un solvant polaire.

1)- Dissolution d’un solide ionique dans l’eau.

     Exemple : dissolution du chlorure de sodium dans l’eau.

-    D’une part le chlorure de sodium est un solide ionique.

-  C’est un empilement compact et ordonné d’ion sodium et d’ions chlorure.

-    D’autre part, l’eau est un solvant polaire.

-    La dissolution du cristal se fait en plusieurs étapes :

►    Première étape : Dissociation du solide ionique.

-    Les ions sodium sont attirés par les pôles négatifs des molécules d’eau et les ions chlorure sont attirés par les pôles positifs des molécules d’eau.

-    Ce phénomène entraîne la diminution des interactions entre les cations et les anions du cristal.

-    Les ions sodium et chlorure se dissocient du cristal ionique.

►    Deuxième étape : Hydratation des ions.

-    Les ions sodium Na⁺ et les ions chlorure Cl^– s’entourent d’un cortège de molécules d’eau.

-  Ils sont hydratés.

 

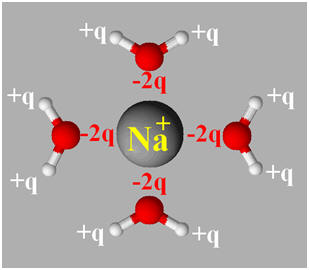
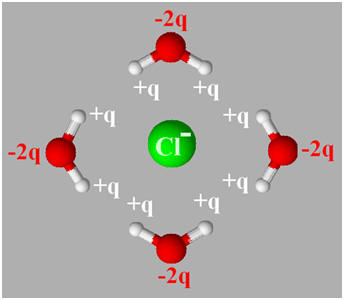
►    Troisième étape : La dispersion des ions.

-    Les ions hydratés se déplacent dans le solvant et s’éloignent sous l’effet de l’agitation thermique.

-    Ils se dispersent dans l’eau avec leur cortège respectif de molécules d’eau.

-    Ce cortège masque en partie la charge portée par les ions et empêche l’agrégation des ions.

    La dissolution d’un cristal ionique dans un solvant polaire se déroule en 3 étapes :

-    La dissociation des ions du solide ;

-    La solvatation des ions ;

-    La dispersion des ions dans le solvant.

    Les solides ioniques sont très solubles dans les solvants polaires.

-    Les ions s’entourent dans ce cas de molécules de solvant.

-  On dit qu’ils sont solvatés.

2)- Équation d’une réaction de dissolution dans l’eau d’un solide ionique.

►    Exemple : Cas de la dissolution du chlorure de sodium dans l’eau.

-    La formule du cristal : NaCl (s)

-    Formule des ions hydratés : on utilise la notation simplifiée suivante :

-    Na⁺ (aq) et Cl^– (aq)

-    On ne précise pas le nombre de molécules d’eau qui entoure chaque ion.

-    Équation de dissolution :

    Règles de conservation :

-    L’équation de dissolution doit respecter la conservation des éléments chimiques et la conservation de la charge.

►    Application : On dissout de la fluorine (fluorure de calcium CaF₂) dans l’eau.

Écrire l’équation de dissolution. Formule de l’ion fluorure : F^–.

-    Réponse :

 

III- Dissolution d’un composé moléculaire dans un solvant.

1)- Dissolution d’un soluté polaire dans un solvant polaire.

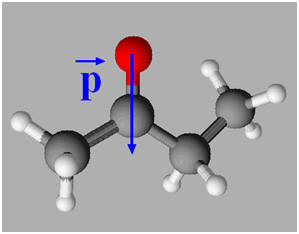
a)-  Premier cas : Il n’y a pas formation de liaisons hydrogène.

     On verse quelques gouttes de butanone dans de la propanone (acétone : solvant industriel).

-    On agite.

-    On obtient une solution homogène.

-    Le soluté est la propanone et le solvant l’acétone.

-    La butanone, soluté polaire et soluble dans un solvant polaire la propanone.

-    La solubilité est liée au fait que des interactions de Van Der Waals s’établissent entre les molécules polaires de soluté et les molécules polaires de solvant.

    Conclusion : les solutés polaires sont solubles dans les solvants polaires.

 

b)-  Deuxième cas : il a formation de liaisons hydrogène.

     Exemple 1 : On verse de l’eau sur un morceau de sucre placé dans un bécher.

Le sucre est du saccharose de formule C₁₂H₂₂O₁₁ (s).

-    On agite. On obtient une solution homogène.

-   C’est de l’eau sucrée : solution aqueuse de saccharose.

-    Cette solution ne conduit pas le courant électrique.

-    Cette solution est constituée de molécules de saccharose parmi des molécules d’eau.

-    La molécule de saccharose est une molécule polaire du fait de la présence de plusieurs liaisons polarisées C – O et O – H.

 

 

Molécule 3D 

Vidéo Molécule 3D

-    La molécule d’eau est une molécule polaire du fait de la présence de deux liaisons polarisées O – H.

-    La grande solubilité du saccharose dans l’eau résulte :

-    Des interactions de Van Der Waals qui interviennent entre les molécules de soluté (le saccharose) et les molécules de solvant (eau) ;

-    Et la formation de nombreuses liaisons hydrogène qui s’établissent entre les molécules de soluté (le saccharose) et les molécules de solvant (eau).

-     Équation de dissolution :

     Exemple 1 : On verse délicatement quelques gouttes d’acide sulfurique H₂SO₄ (ℓ) dans une fiole jaugée contenant de l’eau.

-    On agite. On obtient une solution homogène.

-  C’est une solution aqueuse d’acide sulfurique.

-    La solution obtenue conduit le courant électrique.

-    Dans le cas présent l’interaction entre le soluté et le solvant est tellement importante que certaines liaisons covalentes du soluté sont rompues.

-    On obtient des ions hydrogène hydratés H⁺ (aq) (autre notation H₃O⁺) et des ions sulfate SO₄^2– (aq) dans la solution.

-    Équation de dissolution :

    Conclusion : les solutés polaires sont solubles dans les solvants polaires.

-    La solubilité d’un soluté polaire dans un solvant polaire est favorisée lorsque des liaisons hydrogène se forment entre les molécules de soluté et les molécules de solvant.

2)- Dissolution d’un soluté apolaire dans un solvant apolaire.

     Expérience 1 : Diiode dans l’eau :

-    La molécule de diiode est une molécule apolaire.

-    On verse quelques cristaux de diiode dans un tube à essais contenant de l’eau (solvant polaire).

-    On agite. La solution prend une teinte jaune-orangé et il reste du diiode solide au fond du tube à essais.

 

-    Le diiode soluté apolaire est peu soluble dans l’eau, solvant polaire.

     Expérience 2 : Diiode dans l’heptane.

-     On rajoute environ 3 mL d’heptane (incolore), solvant apolaire, dans le tube à essais.

-    L’heptane est non miscible dans l’eau et moins dense que l’eau.

-  On le verse délicatement, l’heptane se situe au dessus de la phase aqueuse.

-    On agite et on laisse décanter.

 

-    On remarque que l’heptane initialement incolore prend une teinte fuchsia et la solution aqueuse s’éclaircie.

-  Le diiode au fond du tube à essais a disparu.

-    Le diiode, soluté apolaire, est soluble dans le solvant apolaire alors qu’il est très peu soluble dans un solvant polaire.

    Les solutés moléculaires apolaires ou peu polaires sont généralement solubles dans les solvants apolaires.

 

IV- Détermination de la concentration d’un ion en solution.

1)- Concentration molaire en soluté apporté.

    Relation :

-    La concentration molaire volumique C (s) en soluté apporté est égale au quotient de la quantité de matière n (s) en soluté apporté par le volume V de la solution :

►    Application 1 :

-    On prépare une solution aqueuse de sulfate de sodium Na₂SO₄ (s).

-    Pour ce faire, on dissout une masse m = 14,2 g de soluté dans l’eau.

-    Le volume de la solution obtenue est V = 0,500 L.

-    Déterminer la concentration en soluté apporté de cette solution.

►    Réponse :

-    Concentration de la solution en soluté apporté :

-    Relation 1 :

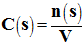
-    Relation 2 :

-    En combinant 1 et 2, il vient :

-     

-    Masse molaire du soluté :

-     

-    Concentration en soluté apporté :

-     

2)- Concentration molaire d’une espèce dissoute.

-    Soit X l’espèce dissoute.

-  L’espèce X peut être une molécule ou un ion.

-    Notation de la concentration de l’espèce chimique en solution : [X]

    Relation :

►    Application 2 : Déterminer la concentration en ions sodium et en ions sulfate de la solution précédente.

►    Réponse :

-    Pour pouvoir résoudre cet exercice, il faut utiliser l’équation de dissolution.

-    Le mieux maintenant est de travailler avec un tableau d’avancement pour déterminer l’état final et avoir le bilan de quantité de matière.

-    Concentration des ions sulfate.

-     

-    Concentration des ions sodium :

-     

-    Remarque 1 : La concentration effective d’un ion dans la solution peut être différente de la concentration en soluté apporté.

-    Remarque 2 : L’écriture [Na₂SO₄] n’a pas de sens car l’espèce Na₂SO₄ n’existe pas en solution.

-    La formule Na₂SO₄ est une formule statistique, d’un cristal ionique.

-  Elle indique que le cristal est formé d’ions sodium et d’ions sulfate et qu’il y a 2 ions sodium pour un ion sulfate.

 

V- Applications.

(Lien vers Chim N° 02 solutions électrochimiques et concentration. Exercices)

1)- QCM : pour chaque question, indiquer la (ou les) bonne(s) réponse(s).

QCM 01 sous forme de tableau.

QCM 01 réalisé avec le logiciel Questy :

pour s'auto-évaluer.

QCM 02 sous forme de tableau.

QCM 02 réalisé avec le logiciel Questy :

pour s'auto-évaluer.

QCM N° 01 Révisions

QCM N° 01 Questy Révisions

QCM N° 02 Révisions

QCM  N° 02 Questy Révisions

2)- Exercices :  Exercices : énoncé avec correction

a)-  Exercice 7 page 180. Justifier la polarité d’un solvant.

b)-  Exercice 9 page 180. Identifier un solvant polaire ou apolaire.

c)-  Exercice 10 page 180. Expliquer la dissolution d’un solide ionique dans l’eau.

d)-  Exercice 11 page 180. Écrire des équations de dissolution.

e)-  Exercice 12 page 180. Étudier des solutions ioniques.

f)-   Exercice 13 page 180. Expliquer la dissolution de l’acétone dans l’éther.

g)-  Exercice 19 page 181. Concentrations molaires effectives.

h)-  Exercice 22 page 182. Un médicament contre l’anémie.