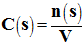|
Chim. N° 05 |
Dissolution de composés ioniques et moléculaires. Exercices. |
|
|
Mots clés : Dissolution, composés ioniques, composés moléculaires, dissolution d'un solide ionique dans un solvant polaire, solide ionique, solvant polaire, dissolution d'un solide ionique dans l'eau, équation de dissolution, dissolution d'un composé moléculaire dans un solvant, solvant polaire, solvant apolaire, dissolution d'un soluté apolaire dans un solvant apolaire, Soluté, solvant, solution, solution aqueuse, concentration molaire volumique, concentration molaire en soluté apporté, concentration molaire d'une espèce dissoute, concentration effective, QCM, polarité d"un solvant, identifier un solvant polaire, identifier un solvant apolaire, expliquer la dissolution d'un solide ionique, écrire des équations de dissolution, expliquer la dissolution de l'acétone dans l'éther, concentrations molaires effectives, médicament contre l'anémie, permanganate de potassium, bromoéthane, éthanol, méthoxyméthane, éthoxyéthane, éther, acétone, propanone, phosphate de potassium, sulfate de potassium, ion fer II, orthophénanthroline, o-phénanthroline, réaction de complexation, ammoniac, molécule d'ammoniac, ... |
|
|
I- Exercice 7 page 180. Justifier la polarité d’un solvant.
|
Le modèle moléculaire de la molécule d’ammoniac est donné ci-dessous. Expliquer pourquoi la l’ammoniac liquide est un solvant polaire.
|
|
- L’ammoniac liquide est un solvant polaire : - D’une part : l’azote est plus électronégatif que l’hydrogène. - En conséquence, le doublet de liaison de la liaison H – N est plus proche de l’atome d’azote que de l’atome d’hydrogène. - Il apparaît une charge partielle – q sur l’atome d’azote et une charge partielle positive sur l’atome d’hydrogène. -
- Géométrie de la molécule : - Le schéma de Lewis de la molécule d’ammoniac : -
- L’atome d’ammoniac possède 3 doublets liants et 1 doublet non liant. En définitive, il possède 4 doublets. - Ces doublets vont se placer afin que l’interaction entre les doublets soit minimale. - Ils prennent une disposition tétraédrique : l’angle entre deux doublets est voisin de 109 °.
-
-
La molécule
d’ammoniac possède le moment dipolaire.
C’est un solvant polaire. |
II- Exercice 9 page 180. Identifier un solvant polaire ou apolaire.
|
Le toluène et le dichlorométhane sont deux solvants liquides à température ambiante. Leurs modèles moléculaires sont respectivement :
ou
Identifier, en justifiant, le solvant polaire et le solvant apolaire. On pourra d’aider de schémas si nécessaire. |
|
- La molécule de toluène : - On peut admettre, comme les liaisons C – H sont très peu polarisées que : - Les solvants dont les molécules ne comportent que des atomes de carbone et d’hydrogène sont apolaires. - Ceci, même en l’absence de symétrie de la molécule, - Le toluène est un solvant apolaire. - La molécule de dichlorométhane : - Les liaisons C – H sont très peu polarisées alors que les liaisons C – Cl sont polarisées. -
Cette molécule
possède un moment dipolaire résultant
|
III- ution d’un solide ionique dans l’eau.
|
Le permanganate de potassium est solide ionique violet de formule KMnO4 (s). Une paillette de permanganate de potassium est introduite dans un bécher rempli d’eau, sans agitation (photographie).
1)- Quelles sont systématiquement les trois étapes de la dissolution d’un solide ionique dans l’eau ? 2)- Lors de la dissolution, les ions potassium K+ (aq) et les ions permanganate MnO4– (aq) sont « hydratés ». Qu’est-ce que cela signifie ? 3)- En représentant les ions par des sphères, schématiser l’hydratation des ions par des molécules d’eau. 4)- Écrire l’équation de dissolution de ce solide. |
|
1)- Les trois étapes de la dissolution d’un solide ionique dans l’eau : ► Première étape : Dissociation du solide ionique. - Les ions potassium sont attirés par les pôles négatifs des molécules d’eau et les ions permanganate sont attirés par les pôles positifs des molécules d’eau. - Ce phénomène entraîne la diminution des interactions entre les cations et les anions du cristal. - Les ions potassium et permanganate se dissocient du cristal ionique. ► Deuxième étape : Hydratation des ions. - Les ions potassium K+ et les ions permanganate MnO4– s’entourent d’un cortège de molécules d’eau. Ils sont hydratés. ► Troisième étape : La dispersion des ions. - Les ions hydratés se déplacent dans le solvant et s’éloignent sous l’effet de l’agitation thermique. - Ils se dispersent dans l’eau avec leur cortège respectif de molécules d’eau. - Ce cortège masque en partie la charge portée par les ions et empêche l’agrégation des ions. 2)- Les ions potassium K+ (aq) et les ions permanganate MnO4– (aq) sont « hydratés » : - Ils s’entourent d’un cortège de molécules d’eau. 3)- Schématisation de l’hydratation des ions par des molécules d’eau
4)- Équation de dissolution de ce solide :
|
IV- ge 180. Écrire des équations de dissolution.
|
Recopier, puis compléter les équations de dissolutions suivantes :
|
|
Tableau complété :
|
V- Exercice 12 page 180. Étudier des solutions ioniques.
|
Le méthoxyméthane et l’éthanol sont deux molécules dont les modèles moléculaires sont donnés ci-dessous :
1)- Qu’appelle-t-on molécules isomères ? 2)- Comment expliquer que ces deux molécules sont solubles dans le solvant polaire bromoéthane CH3 – CH2 – Br ? 3)- À 20 ° C, la solubilité du méthoxyméthane dans l’eau est de 71 g / L alors que l’éthanol et l’eau sont miscibles en toutes proportions. Interpréter cette différence de solubilité. |
|
1)- Molécules isomères : - Deux molécules isomères ont même formule brute mais des enchaînements d’atomes différents. - Les isomères ont des propriétés physiques et chimiques différentes et constituent des espèces chimiques distinctes. 2)- Solubilité dans le solvant polaire bromoéthane CH3 – CH2 – Br - La molécule de méthoxyméthane possède deux liaisons C – O qui sont polarisée, car l’oxygène est plus électronégatif que le carbone. - Comme l’enchainement C – O – C est coudée, le moment dipolaire résultant de la molécule de méthoxyméthane n’est pas nul. - Le méthoxyméthane est un solvant polaire. - De même la molécule d'éthanol possède une liaison C – O polarisée et une liaison O – H polarisée. - La liaison O – H est plus polarisée que la liaison C – O. De plus l’enchainement H – O – C est coudée, - le moment dipolaire résultant n’est pas nul. - L’éthanol est une molécule polaire. - Les solutés polaires sont solubles dans les solvants polaires. 3)- Différence de solubilité : - L’éthanol est soluble dans l’eau en toutes proportions alors que le méthoxyméthane non. - Pour l’éthanol : - Les molécules d’éthanol peuvent former des liaisons hydrogène entre elles : - Elles peuvent former des liaisons hydrogène avec les molécules d’eau. - Pour le méthoxyméthane - Les molécules de méthoxyméthane ne peuvent pas former de liaisons hydrogène entre elles car les liaisons C – H ne sont pas assez polarisées. - Elles peuvent former des liaisons hydrogène avec les molécules d’eau - L’éthanol est plus solubles dans l’eau que le méthoxyméthane car il y a plus de liaison hydrogène dans la solution. - La solubilité d’un soluté polaire dans un solvant polaire est favorisée lorsque des liaisons hydrogène se forment entre les molécules de soluté et les molécules de solvant. |
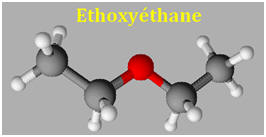
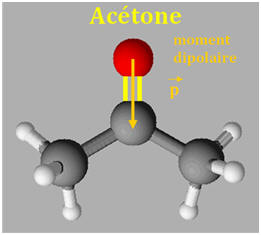
VI- ice 13 page 180. Expliquer la dissolution de l’acétone dans l’éther.
|
L’acétone et l’éthoxyéthane (éther) sont deux solvants couramment utilisés en chimie. Leurs modèles moléculaires sont respectivement :
1)- Ces deux solvants sont-ils polaires ? 2)- Justifier que l’acétone et l’éthoxyéthane soient miscibles en toutes proportions. 3)- Quelle interaction est responsable de cette miscibilité ? |
|
1)- Solvants polaires : - La molécule d’acétone possède une liaison C = O qui est polarisée car le carbone est moins électronégatif que l’oxygène. Les liaisons C – H sont peu polarisées.
- La molécule d’acétone est une molécule polaire. - La molécule d’éthoxyéthane possède deux liaisons C – O qui sont polarisées. L’enchainement C – O – C étant coudé, le moment dipolaire résultant de la molécule n’est pas nul.
- La molécule d’éthoxyéthane est une molécule polaire. 2)- Justification de la miscibilité : - Un soluté polaire est soluble dans un solvant polaire. - Comme les deux molécules sont polaires, elles sont miscibles l’une dans l’autre et inversement. 3)- Interaction : - Des interactions de Van Der Waals interviennent entre les molécules de soluté et les molécules de solvants du fait de l’existence de dipôles permanents. - L’interaction de Van Der Waals résulte de l’interaction entre dipôles électriques. - Dans ces molécules, il y a des interactions électrostatiques entre les dipôles qui sont des dipôles permanents. - La solubilité est liée au fait que des interactions de Van Der Waals s’établissent entre les molécules polaires de soluté et les molécules polaires de solvant. |
VII- Exercice 19 page 181. Concentrations molaires effectives.
|
On considère une solution aqueuse S1 de sulfate de potassium K2SO4 et une solution aqueuse S2 de phosphate de potassium K3PO4. Les deux solutions ont même concentration molaire effective en ion potassium K+ (aq) : [K+] = 0,60 mol / L. 1)- Écrire les équations de dissolution dans l’eau des deux composés ioniques K2SO4 (s) et K3PO4 (s). 2)- Calculer les concentrations molaires des deux solutions en soluté apporté. 3)- En déduire les concentrations molaires des anions dans les deux solutions. |
|
1)- Équations de dissolutions :
2)- Concentrations molaires des deux solutions en soluté apporté : - La concentration molaire volumique C (s) en soluté apporté est égale au quotient de la quantité de matière n (s) en soluté apporté par le volume V de la solution : -
► Solution S1 de sulfate de potassium K2SO4 de concentration en soluté apporté C1.
- On connait : [K+] = 0,60 mol / L - On en déduit la valeur de la concentration C1 de la solution S1. - C1 ≈ 0,60 / 2 - C1 ≈ 0,30 mol / L. ► Solution aqueuse S2 de phosphate de potassium K3PO4 de concentration en soluté apporté C2.
- On connait : [K+] = 0,60 mol / L - On en déduit la valeur de la concentration C2 de la solution S2. - C2 ≈ 0,60 / 3 - C2 ≈ 0,20 mol / L. 3)- Concentrations molaires des anions dans les deux solutions : ► Solution S1 de sulfate de potassium K2SO4 de concentration en soluté apporté C1.
► Solution aqueuse S2 de phosphate de potassium K3PO4 de concentration en soluté apporté C2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
VIII- Exercice 22 page 182. Un médicament contre l’anémie.
|
A- Première partie : Un médicament, contenant des ions fer II Fe2+, se présente sous forme de comprimés. On cherche à vérifier la teneur en ion fer II Fe2+ en effectuant un dosage spectrophotométrique. En présence d’une solution incolore d’o-phénanthroline, les ions fer II Fe2+ (aq) réagissent avec apparition d’une coloration rouge-orangé. La concentration effective des ions Fe2+ (aq) de cette solution peut alors être déterminée par la mesure de l’absorbance de la solution pour une longueur d’onde λ = 500 nm. 1)- Pourquoi choisir une longueur d’onde λ = 500 nm pour ces mesures d’absorbance au spectrophotomètre ? 2)- Pourquoi la solution d’o-phénanthroline doit-elle être introduite en excès par rapport aux ions fer II ? - À partir d’une solution S de concentration massique t = 20,0 x 10 – 3 g / L en ions fer II et en présence d’o-phénanthroline, on réalise une échelle de teinte. - Le graphe donnant l’évolution de l’absorbance A en fonction de la concentration massique t en ions Fe2+ (aq) est donné ci-dessous. Tableau de valeurs :
3)- En exploitant ce graphe, établir la relation numérique entre les grandeurs A et t en précisant les unités. B- Deuxième partie : On écrase un comprimé du médicament dans un mortier. La totalité du comprimé écrasé est introduite dans une fiole jaugée de 1000 mL. On complète avec de l’eau distillée et on agite longuement la solution. La solution S0 obtenue est incolore. Dans une fiole jaugée de 50,0 mL, on verse 5,0 mL de solution S0, puis on ajoute de l’o-phénanthroline dans les mêmes proportions que celles utilisées pour préparer l’échelle de teinte. La fiole est complétée avec de l’eau distillée : soit S’0 la solution obtenue. L’absorbance de la solution S’0 pour λ = 500 nm est égale à A’ = 1,45. 1)- Déterminer la concentration massique t’0 en ion Fe2+ (aq) de la solution S’0. En déduire la concentration massique t0 en ion Fe2+ (aq) de la solution S0. 2)- Calculer la masse d’ions Fe2+ (aq) contenue dans un comprimé. 3)- D’après la notice, la masse de « sulfate ferreux sesquihydraté » dans un comprimé est de 256,30 mg alors que la masse d’ions fer II Fe2+ est de 80 mg. En notant {FeSO4, n H2O} la formule du sulfate ferreux sesquihydraté, montrer que n = 1,5. |
|
A- Première partie : 1)- Choix de longueur d’onde λ = 500 nm pour ces mesures d’absorbance au spectrophotomètre : - En présence d’une solution incolore d’o-phénanthroline, les ions fer II Fe2+ (aq) « réagissent » (réaction de complexation) avec apparition d’une coloration rouge-orangé. - Formule topologique de l’o-phénanthroline :
- Spectre de la lumière blanche : - Couleur correspondante à λ = 500 nm :
Synthèse soustractive
Synthèse additive - Courbe A = f (λ) :
- On remarque que la solution absorbe principalement dans le vert et le bleu clair (cyan). - La couleur de la solution se situe entre le rouge et le magenta. - La solution a une teinte « rouge-orangé ». - Pour réaliser les mesures d’absorbance, le spectrophotomètre est généralement réglé sur la longueur d’onde λmax
correspondant au
maximum d’absorption du spectre de
la solution étudiée. - À cette longueur d’onde, la valeur de l’absorbance étant la plus grande, l’incertitude sur la mesure est la plus petite. - On n’a pas choisi λ = 510 nm pour éviter que le spectrophotomètre sature en fin d’expérience lorsque la concentration en ions fer II atteint 10 mg / L. 2)- Solution d’o-phénanthroline doit-elle être introduite en excès par rapport aux ions fer II : - Ainsi le réactif limitant de la réaction est l’ion fer II. - On sait alors que tous les ions fer II participent à la réaction de complexation. - Tous les ions fer II ont été consommés. 3)- Exploitation du graphe : - Les points sont sensiblement alignés. La droite moyenne passe par l’origine. - Il y proportionnalité entre la concentration massique t et l’absorbance A de la solution. - A = k . t. - Détermination de k : - La droite obtenue est du type : y = a . x - La grandeur a représente le coefficient directeur de la droite tracée, c’est le coefficient de proportionnalité k. - L’exploitation graphique donne : -
- A ≈ 0,18 C avec A sans unité, C en mg / L et a = k ≈ 0,18 L / mg.
B- Deuxième partie : 1)- Concentration massique t’0 en ion Fe2+ (aq) de la solution S’0 : - La solution S’0 a une absorbance A’ = 1,45. - L’exploitation graphique donne : - t’0 ≈ 8,0 mg / L - Concentration massique t0 en ion Fe2+ (aq) de la solution S0 : -
Pour préparer S’0,
on a effectué une dilution de la solution S0.
- Au cours de la dilution, il y a conservation de la quantité de matière de soluté et donc conservation de la masse de soluté : - t0 . V0 = t’0 . V’0 - t0 = 10 t’0 ≈ 80 mg / L. 2)- Masse d’ions fer Fe2+ (aq) contenue dans un comprimé : - La totalité du comprimé écrasé est introduite dans une fiole jaugée de 1000 mL. - On a prélevé 5,0 mL de cette solution pour préparer la solution S’0. - En conséquence, dans un litre de solution S0, il y a 80 mg d’ions Fe2+ (aq). 3)-
La valeur de n dans la formule : FeSO4,
n H2O : - La masse de « sulfate ferreux sesquihydraté » dans un comprimé est de 256,30 mg alors que la masse d’ions fer II Fe2+ est de 80 mg. - Masse molaire du sulfate ferreux sesquihydraté : - M (Fe) = 56 g / mol ; M (S) = 32 g / mol ; M (O) = 16 g / mol ;
-
M
(H2O) = 18 g / mol
-
M
(FeSO4, n H2O)
= M (Fe) + M (SO4)
+ n M (H2O)
-
M
(FeSO4, n H2O)
= 56 + 96 + 18 n =
152 + 18 n
-
|
|
|








 et
et