I- La lunette astronomique.

1)- Rappels et compléments.

►  La lentille convergente.

-  C’est une lentille qui réfracte les rayons lumineux parallèles à l’axe optique de manière à les rapprocher de celui-ci.

-  Elle fait converger les rayons lumineux parallèles à l’axe optique.

-  Elles sont plus épaisses au centre qu’aux bords.

-  Une lentille mince est caractérisée par trois points particuliers :

-  Son centre optique O ;

-  Son foyer image F’ ;

-  Son foyer objet F.

-  Représentation symbolique :

-  La distance focale d’une lentille convergente :

-  La distance focale f’ est définie comme la distance entre le centre optique O et chacun des foyers F et F’.

-  On la note f’ :

-  Le foyer objet F et le foyer image F’ sont symétriques par rapport au centre optique O.

-  La loi du retour inverse de la lumière permet de dire que tout rayon passant par F, symétrique de F’ par rapport au centre optique O émerge parallèlement à l’axe optique Δ.

►  Construction d’une image réelle :

-  Application :

-  Données : Diamètre de la lentille : 6,0 cm

-  Distance focale : f’ = 2,0 cm

-  L’objet est perpendiculaire à l’axe optique.

-  Objet AB = 1,0 cm

-  L’objet AB est situé avant le foyer-objet à 1,5 cm du foyer-objet.

-  Réaliser la construction en utilisant la méthode suivante :

-  Rayon 1 : issu du point B et passant par le centre optique : il n’est pas dévié.

-  Rayon 2 : issu du point B et parallèle à l’axe optique. Il émerge de la lentille en passant par le point F’ foyer - image.

-  Rayon 3 : issu du point B et passant par F (foyer - objet). Il émerge de la lentille parallèlement à l’axe optique.

-  Repère associé à un lentille mince convergente :

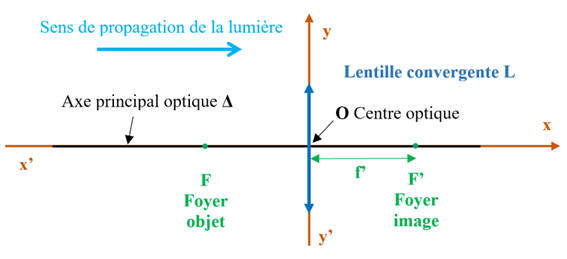
-  Relation de conjugaison :

-  Formule de conjugaison avec les notations choisies :

-   

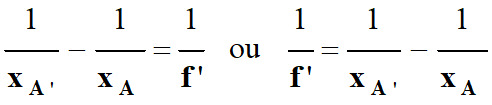
-  Formule de conjugaison avec les mesures algébriques :

-   

-  Formule de Descartes :

-   

-  Grandissement de l’image :

-  Le grandissement d’une lentille est donné par la relation :

-   

-  Avec le repère lié à la lentille mince convergente :

-   et

-  Le grandissement de l’image est donné par la relation suivante :

-   

-  La grandeur γ est un nombre qui n’a pas d’unité.

-  C’est une grandeur algébrique : elle peut être positive ou négative.

-  Si γ > 0 l’image a le même sens que l’objet, on dit qu’elle est droite.

-  Si γ < 0 l’image est de sens contraire à l’objet, on dit qu’elle est renversée.

-  Si | γ | >1, l’image est plus grande que l’objet.

-  Si| γ | <1 , l’image est plus petite que l’objet.

►  La lentille divergente :

-  C’est une lentille qui réfracte les rayons lumineux parallèles à l’axe optique de manière à les éloigner de celui-ci.

-  Elle fait diverger les rayons lumineux parallèles à l’axe optique.

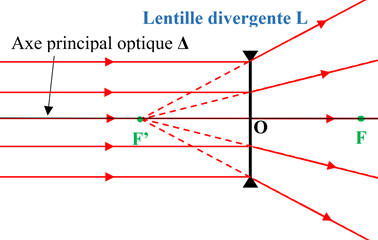
-  Elles sont plus épaisses aux bords qu’au centre.

-  Représentation symbolique :

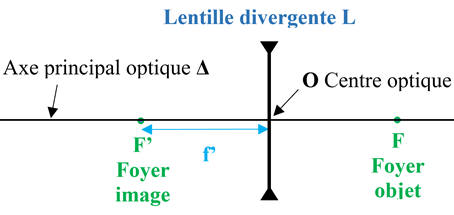
-  La distance focale d’une lentille divergente :

-  On la note f’ :

-  Elle est négative pour une lentille divergente.

►  Image donnée par une lentille divergente : Objet réel et image virtuelle 

-  L’image est droite, plus petite que l’objet et elle est virtuelle.

►  Objet virtuel et image réelle :

-  L’image est droite, plus grande que l’objet et elle est réelle.

►  Objet virtuel et image virtuelle :

-  L’image est renversée, plus grande que l’objet et elle est virtuelle.

2)- Constitution de la lunette astronomique.

-  La lunette astronomique permet d’observer des objets célestes,  c’est-à-dire des objets éloignés (que l’on peut considérer comme situés à l’infini).

-  Une lunette astronomique est constituée :

-  D’un objectif situé du côté de l’objet que l’on observe et

-  D’un oculaire situé du côté de l’œil.

-  Le diamètre de l’objectif doit être le plus grand possible pour collecter le maximum de lumière provenant de l’objet céleste situé à l’infini.

-  L’objectif est le collecteur de lumière.

-  L’objectif qui donne d’un objet éloigné une image dans son plan focal image,

-  Un oculaire qui joue le rôle de la loupe.

-  Le chercheur permet d’aligner la visée sur l’objet céleste que l’on veut observer.

-  Remarque : l’œil observe l’image donnée par l’objectif par l’intermédiaire de l’oculaire.

-  La mise au point se fait en modifiant la longueur du tube entre l’oculaire et l’objectif.

►  Lunette astronomique du commerce : 70 / 700 Az2

-  Les constructeurs précisent le diamètre de l’objectif et sa distance focale.

-  La lunette est livrée le plus souvent avec plusieurs oculaires.

-  Caractéristiques de cette lunette astronomique :

-  La distance focale de l’oculaire est toujours plus petite que celle de l’objectif.

3)- Modélisation.

-  L’objectif et l’oculaire d’une lunette astronomique sont modélisées par deux lentilles minces convergentes L₁ et L₂.

-  Elles ont le même axe optique Δ.

►  Lunette astronomique afocale :

-  Lorsque le foyer image F’₁ de l’objectif et le foyer objet F₂ de l’oculaire sont confondus, on est en présence d’une lunette afocale.

4)- Construction d’une image :

-  on modélise l’objectif et l’oculaire par deux lentilles minces convergentes.

-  Matériel : Lentille L₁ : f’₁ = 250 mm ; Lentille L₂ : f’₂ = 50 mm

-  distance entre les deux lentilles : O₁O₂ = 280 mm ;

-  Angle sous lequel l’Astre est vu à l’œil nu : θ = 3 °.

-  Remarque :

-  On appelle diamètre apparent, l’angle sous lequel l’astre est vu à l’œil nu.

-  Il s’exprime en radian.

  Construire l’image d’un astre donnée par cette lunette : Échelle 1/2.

  Comment doit-on régler le dispositif pour que l’œil observe sans fatigue l’image finale A’’B’’  ?

-  Si l’on veut que l’œil n’accommode pas, l’image A’’B’’ doit se trouver au Punctum Remotum de l’observateur.

-  Si l’observateur possède une vue normale, alors l’image A’’B’’ se trouve à l’infini.

-  En conséquence, F’₁ et F₂ sont confondus : on dit que la lentille est afocale.

-  L’œil normal :

-  La distance cristallin - rétine étant invariable, l’œil accommode pour observer des objets rapprochés.

-  Un œil normal peut voir nettement des objets :

-  Situés entre l’infini et le punctum remotum P.R. (à l’infini pour un œil normal et une distance finie pour un œil myope).

-  Et possède une distance minimale de vision distincte : le punctum proximum P.P. en accommodant de plus en plus (23 cm environ pour un œil normal).

-  L’œil :

-  L’œil 

II- La construction du faisceau traversant une lunette afocale.

1)- Lunette afocale.

►  Une lunette est afocale lorsque le foyer principal image de l’objectif coïncide avec le foyer principal objet de l’oculaire.

2)- Construction :

-  Matériel : Lentille L₁ : f’₁ = 17,2 mm ; Lentille L₂ : f’₂ = 30 mm ; tubes en carton.

-  Angle sous lequel l’Astre est vu à l’œil nu : θ = 3 °.

  Construire l’image d’un astre donnée par cette lunette : échelle ½

III- Grossissement d’une lunette afocale.

1)- Définition.

-  Le grossissement d’une lunette est le rapport entre :

-  L’angle θ sous lequel l’objet est vu à l’œil nu et

-  L’angle θ’ sous lequel son image est vue à travers la lunette.

-  Ainsi l’objet éloigné (B ∞) est vu sous l’angle θ et l’image A’B’ est vue sous l’angle θ’.

-  Le grossissement G d’une lunette est donné par la relation suivante :

2)- Exemple : Expression du grossissement d’une lunette afocale.

-  Exploitation du schéma suivant :

-  Étude de la lunette afocale :

-  Le point A’ est l’image du point A (situé à l’infini) donnée par l’objectif de la lunette.

-  Le point A’ est confondu avec le foyer image F’₁ de l’objectif et le foyer objet F₂ de l’oculaire.

-  L’image A’B’ de l’objet AB est perpendiculaire à l’axe optique Δ.

-  Considérons le triangle O₁F’₁B’ rectangle en F’₁ :

-   

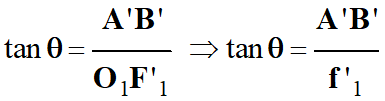
-  Considérons le triangle O₂F₂B’ rectangle en F₂ :

-   

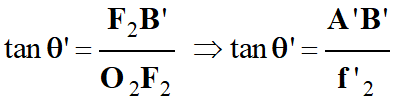
-  Les angles θ et θ’ étants petits (en radian), on peut faire l’approximation des petits angles :

-  Il faut exprimer θ et θ’ en radian :

-  tan θ ≈ θ et tan θ’ ≈ θ’

-  Dans ce cas :

-   

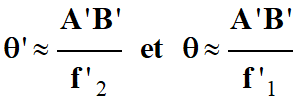
-  On en déduit la relation suivante pour une lunette afocale :

-   

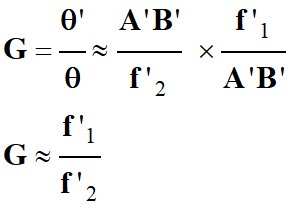
-  Grossissement d’une lentille afocale :

-  Grossissement dans le cas du schéma suivant :

-  Avec la relation faisant intervenir les angles θ et θ’ :

-   

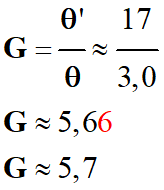
-  Avec la relation faisant intervenir les distances focales de l’objectif et de l’oculaire :

- 

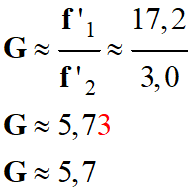
-  On remarque, bien que l’angle θ’ ≈ 17 °, les valeurs sont cohérentes :

-  Car si on exprime les angles en radian :

-  θ’ ≈ 17 ° ≈ 0,29 rad et θ ≈ 3,0 ° ≈ 0,052 rad

-  Ainsi : tan (0,29) ≈ 0,298 et tan (0,052) ≈ 0,0520 

►  Fonctionnement de la lunette afocale :

-  Une lunette afocale donne d’un objet AB situé à l’infini une image A’’B’’ situé à l’infini.

-  Pour l’œil, cette image A’’B’’ devient un objet situé à l’infini.

-  L’image se forme sur la rétine et l’œil n’a pas besoin d’accommoder.

-  Il ne fatigue pas.

►  Grandeurs caractéristiques d’une lunette astronomique :

-  Le diamètre de son objectif exprimé en millimètre (c’est le collecteur de lumière).

-  La distance focale de son objectif exprimée en millimètre.

-  On donne aussi la distance focale des différents oculaires qui accompagnent la lunette astronomique.

-  Ainsi, on peut connaître le grossissement de la lunette astronomique afocale suivant l’association réalisée (objectif, oculaire).

IV- Application

1)- La lunette de Galilée.

2)- QCM :

3)- Exercices :  

 

Exercices : énoncé avec correction DS 1)- Exercice 02 page 396 : Reconnaitre la schématisation d’une lunette afocale. 2)- Exercice 04 page 396 : Identifier un faisceau lumineux. 3)- Exercice 06 page 397 : Représenter le faisceau émergeant d’une lentille afocale. 4)- Exercice 09 page 397 : Tracer l’image d’un objet situé à l’infini 5)- Exercice 11 page 398 :  établir le grossissement d’une lunette afocale. 6)- Exercice 15 page 398 :Trajet d’un faisceau lumineux. 7)- Exercice 16 page 399 : Lunette de laboratoire. 8)- Exercice 20 page 400 : l’étoile Albireo. 9)- Exercice 24 page 402 : DS N° 01 Grossissement et œil réduit (40 min) 10)- Exercice 25 page 403 : DS N° 02 Et la lumière fut (40 min). 11)- Préparation à l’ECE : réalisation d’une lunette astronomique.