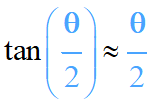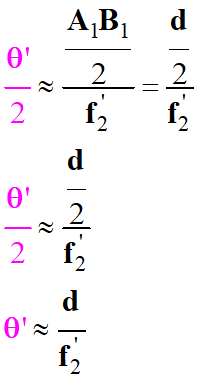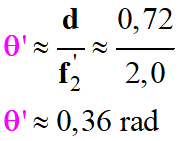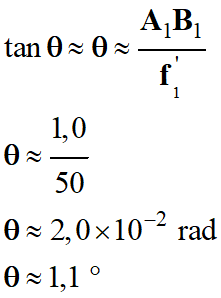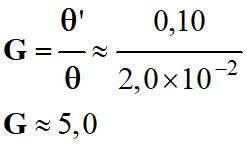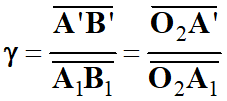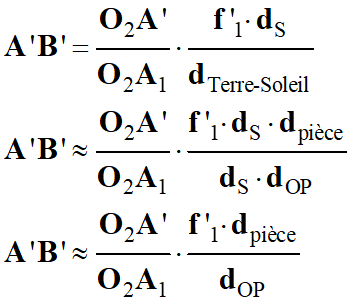Chap N° 19 Exercices 2024 : La lunette astronomique
|
|
I-
Exercice :
Observation de la Lune.
1)- Énoncé.
La Lune peut être vue depuis la terre sous un angle
θ = 9,0 × 10–3 rad.
Elle est observée plus en détails avec une lunette astronomique afocale dont
l'axe optique passe par le centre de la Lune.
Cette lunette dispose d'un ange d'objectif de distance focale
f’1 = 80 cm et d'un
oculaire de distance focale f’2 = 2,0
cm.
On considère deux points objets réels
A et B situés à la surface de la Lune, diamétralement opposés et
symétriques l'un de l'autre par rapport à l'axe optique de la lunette.

a)-
Calculer le diamètre d de l'image intermédiaire
formée par l'objectif.
b)-
Déterminer l'angle θ’ sous lequel l'image de la Lune est vue à
travers la lunette afocale.
c)-
Calculer le grossissement.

2)- Correction.
a)-
Diamètre d
de l'image intermédiaire formée par l'objectif.
►
Lunette astronomique afocale :
-
Une lunette est afocale lorsque le
foyer principal image de l’objectif coïncide avec le foyer principal objet de
l’oculaire.
-
La Lune :

-
On peut considérer que l’objet
AB est situé à l’infini.
-
On trace le rayon lumineux issu du
point B et qui passe par le
centre optique O1
de l’objectif (ce rayon lumineux n’est pas dévié)
-
On trace le rayon lumineux issu du
point A et qui passe par le
centre optique O1
de l’objectif (ce rayon lumineux n’est pas dévié)
-
L’image A1B1
est située dans le plan focal image de l’objectif
-
Plan focal image de l’objectif :
Plan perpendiculaire à l’axe optique contenant le foyer image
F’1.
-
Schéma de la situation :

-
Diamètre
d de l'image intermédiaire formée par l'objectif :
-
d =
A1B1
-
Pour des raisons de de symétrie,
on peut écrire la relation suivante :
-

-
On peut faire l’approximation des
petits angles :
-
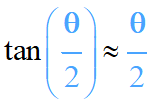
-

-
Application numérique :
-
d ≈ θ ×
f’1 = 9,0 × 10–3
× 80
-
d ≈
0,72 cm
-
d ≈
7,2 mm
b)-
Angle θ’
sous lequel l'image de la Lune est vue à travers la lunette afocale.
-
On trace le rayon lumineux issu du
point B1
et qui passe par le centre optique O2
de l’oculaire (ce rayon lumineux n’est pas dévié)
-
On trace le rayon lumineux issu du
point A1
et qui passe par le centre optique O2
de l’oculaire (ce rayon lumineux n’est pas dévié)
-
Schéma de la situation :

- 
-
On peut faire l’approximation des
petits angles :
- 
-
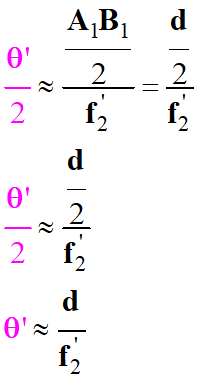
-
Application numérique :
-
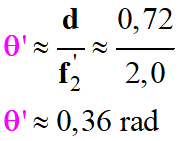
c)-
Grossissement de la lunette afocale.
-
Le grossissement d’une lunette est
le rapport entre :
-
L’angle
θ
sous lequel l’objet est vu à l’œil nu et
-
L’angle
θ’
son image est vu à travers la lunette.
-
Ainsi l’objet éloigné (B ∞) est vu sous l’angle
θ
et l’image A’B’
est vu sous l’angle θ’.
-
Le grossissement
G
d’une lunette est donné par la relation suivante :
|

|
|
G
|
Grossissement : nombre sans unité
|
|
θ’
|
L’angle θ’ sous lequel l'image est vue à travers la lunette
|
|
θ
|
L’angle θ
sous lequel l’objet est vu à l’œil nu
|
|
Il faut
exprimer θ’ et θ dans la même unité d’angle (° ou rad)
|
-
Schéma :
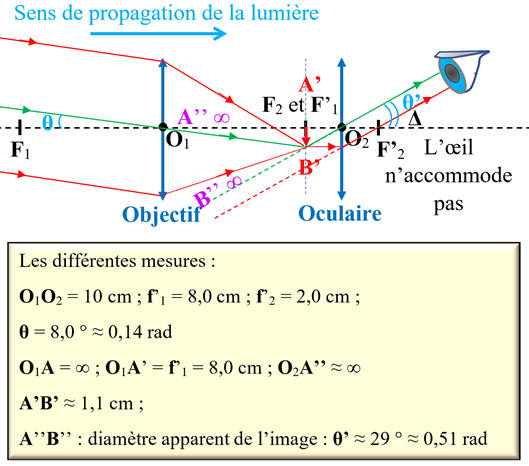
-
Schéma de la situation :

-
Le rayon lumineux issu du point
A1
et parallèle à l’axe optique émerge de l’oculaire (L2)
en passant par le foyer image
F’2.
-
Le rayon lumineux issu du point
B1
et parallèle à l’axe optique émerge de l’oculaire (L2)
en passant par le foyer image
F’2.
-
L’image
A1’B1’
se trouve à l’infini et un œil normal peut observer cette image sans accommoder
-
Grossissement de la lunette
astronomique afocale :
-

-
Application numérique :
-

►
Cas d’une lentille afocale :
-
Grossissement d’une lentille
afocale :
|

|
|
G
|
Grossissement : nombre sans unité
|
|
f’1
|
Distance
focale de l’objectif
|
|
f’2
|
Distance
focale de l’oculaire.
|
|
Il faut
exprimer f’1 et f’2 dans la même
unité (m, cm, mm, …)
|
- 
-
Cette relation découle des
relations suivantes :
-
On a vu que :
-  et
et

-
D’après la définition du
grossissement :
-


II-
Exercice :
Pouvoir séparateur de l’œil.
1)- Énoncé.
Si l’angle sous lequel l'œil observe deux points proches est
inférieur au pouvoir séparateur de l'œil
ε = 3,0 × 10–4 rad,
alors les deux points sont confondus.
Jupiter, la plus grosse planète du Système solaire apparaît ponctuelle à
l'œil nu depuis la Terre.

a)-
Calculer le diamètre apparent θ sous lequel la planète Jupiter
est observée depuis la Terre lorsqu'elle se situe à D = 590 millions de
km.
b)-
Expliquer pourquoi cette planète apparaît ponctuelle depuis la Terre.

2)- Correction.
a)-
Diamètre apparent θ sous lequel la planète Jupiter est observée
depuis la Terre.
-
Distance Terre-Jupiter : D
= 590 ×106 km
-
Rayon de Jupiter : R = 71
492 km
-
Schéma de la situation :
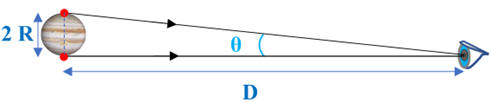
- 
-
Comme D >> R, on
peut faire l’approximation des petits angles en radian :
-

b)-
Jupiter apparaît ponctuelle depuis la Terre :
-
Car θ ≈ 2,42 × 10-4
rad et ε = 3,0 × 10-4 rad
-
θ
< ε
-
La planète Jupiter apparaît comme
ponctuelle depuis la Terre car son diamètre apparent est inférieur au pouvoir
séparateur de l’œil.
L’étoile Albireo
Vision et images
L’œil et la loupe

III- Exercice :
Modélisation d’une lunette afocale.
1)- Énoncé.
Au cours d'une séance de travaux pratiques, un élève modélise
une lunette astronomique à l'aide de lentilles minces convergentes de 4 cm de
diamètre.
La lentille L1 possède
une distance focale égale à 50 cm et la lentille
L2 une distance focale de 10 cm.
a)-
Identifier l'objectif et l'oculaire.
b)-
Déterminer la distance séparant
les centres optiques des 2 lentilles minces convergentes si la lunette est
afocale.
c)-
Réaliser un schéma de la lunette
afocale à l'échelle 1 verticalement et à l'échelle 1/5 horizontalement.
L’élève observe à l'aide de la lunette à focale un objet
AB situé « à l'infini ».
Le point A est sur l'axe optique.
L’image intermédiaire A1B1
un mesure 1,0 cm de hauteur.
d)-
Représenter l'image intermédiaire
A1B1 sur le schéma.
e)-
Calculer l'angle θ sous
lequel l'objet est vu à l'œil nu.
f)-
Construire l'image définitive A’B’.
g)-
Calculer l’angle θ’ sous
lequel l’image définitive est vue à travers la lunette astronomique afocale.
h)-
En déduire le grossissement G
de la lunette afocale.

2)- Correction.
a)-
L'objectif et l'oculaire.
►
Lunette astronomique :
-
La lunette astronomique permet
d’observer des objets célestes,
c’est-à-dire des objets éloignés (que l’on peut considérer comme situés à
l’infini).
-
Une lunette astronomique est
constituée :
-
D’un objectif situé du côté de
l’objet que l’on observe et
-
D’un oculaire situé du côté de
l’œil.

-
Le diamètre de l’objectif doit
être le plus grand possible pour collecter le maximum de lumière provenant de
l’objet céleste situé à l’infini.
-
L’objectif est le collecteur de
lumière.
-
L’objectif qui donne d’un objet
éloigné une image dans son plan focal image,
-
Un oculaire qui joue le rôle de la
loupe.
-
Le chercheur permet d’aligner la
visée sur l’objet céleste que l’on veut observer.
-
Remarque : l’œil observe l’image
donnée par l’objectif par l’intermédiaire de l’oculaire.
►
Lunette astronomique du commerce :
70 / 700 Az2
-
Les constructeurs précisent le
diamètre de l’objectif et sa distance focale.
-
La lunette est livrée le plus
souvent avec plusieurs oculaires.
-
Caractéristique de cette lunette
astronomique :
|
Diamètre de
l’objectif
|
70 mm
|
|
Distance focale
de l’objectif
|
700 mm
|
|
Monture
|
Azimutale
|
|
Oculaires
(distances focales)
|
10 mm et 25 mm
|
|
Grossissement
|
28 X et 70 X
|
-
La distance focale de l’oculaire
est toujours plus petite que celle de l’objectif.
-
La lentille L1,
qui possède une distance focale égale à 50 cm, constitue l’objectif.
-
La lentille L2,
qui possède une distance focale égale à 10 cm, constitue l’oculaire
b)-
Distance séparant les centres
optiques des 2 lentilles minces convergentes.
►
Lunette astronomique afocale :
-
Une lunette est afocale lorsque le
foyer principal image de l’objectif coïncide avec le foyer principal objet de
l’oculaire.
-
Dans le cas présent : le foyer
principal image F’1 de l’objectif coïncide avec le le foyer
principal objet F2 de l’oculaire.
-
Avec f’1 = 50 cm
et f’2 = 10 cm
-
Distance D séparant les
centres optiques des deux lentilles convergentes :
-
D =
f’1 + f’2
-
D =
50 cm + 10 cm
-
D =
60 cm
c)-
Schéma de la lunette afocale.
-
Échelle : 1 verticalement
-
Échelle : 1/5 horizontalement

d)-
Tracer de l'image intermédiaire
A1B1.
-
Le point A est sur l'axe
optique.
-
L’image intermédiaire A1B1
un mesure 1,0 cm de hauteur
-
Le point image A1
du point A situé à l’infini est aussi sur l’axe optique.
-
Il est confondu avec les points
F’1 et F2.
-
Le point B est situé à
l’infini. Son image B1 se trouve dans le plan image de
l’objectif .
-
On représente le rayon lumineux
issu du point B (situé à l’infini) passant par l’axe optique de
l’objectif.. Ce rayon n’est pas dévié.
-
Schéma de la situation :

e)-
Angle θ sous lequel l'objet
est vu à l'œil nu.
-
Exploitation du schéma :
-
Valeur de l’angle θ :
-

-
Comme f’1 = 50
cm et A1B1 = 1,0 cm
-
On peut considérer que f’1
>> A1B1, on peut faire l’approximation des
petits angles en radian :
-
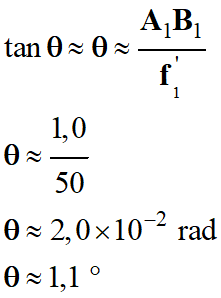
f)-
Construction de l'image définitive
A’B’.
-
On trace le rayon issu du point
B1 qui passe par le centre optique O2.
-
Ce rayon n’est pas dévié.
-
On trace le rayon issu du point
B1 parallèle à l’axe optique qui émerge de la lentille L2
en passant par le foyer image de l’oculaire.
-
Schéma de la situation :

g)-
Angle θ’ sous lequel
l’image définitive est vue à travers la lunette astronomique afocale.
-
Schéma de la situation :

-

-
Si l’on n’utilise pas
l’approximation des petits angles :
-

-
On peut encore faire
l’approximation des petits angles dans ce cas.
h)-
Grossissement G de la
lunette afocale.
-
Définition :
-
Le grossissement d’une lunette est
le rapport entre :
-
L’angle
θ sous lequel l’objet est vu à l’œil
nu et
-
L’angle
θ’ son image est vu à travers la
lunette.
-
Ainsi l’objet éloigné (B ∞) est vu sous l’angle
θ
et l’image A’B’ est vu sous l’angle
θ’.
-
Le grossissement
G d’une lunette est donné par la relation suivante :
|

|
|
G
|
Grossissement : nombre sans unité
|
|
θ’
|
L’angle θ’ sous lequel l'image est vue à travers la lunette
|
|
θ
|
L’angle θ
sous lequel l’objet est vu à l’œil nu
|
|
Il faut
exprimer θ’ et θ dans la même unité d’angle (° ou rad)
|
-
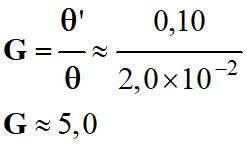
►
Cas d’une lentille afocale :
-
Grossissement d’une lentille
afocale :
|

|
|
G
|
Grossissement : nombre sans unité
|
|
f’1
|
Distance
focale de l’objectif
|
|
f’2
|
Distance
focale de l’oculaire.
|
|
Il faut
exprimer f’1 et f’2 dans la même
unité (m, cm, mm, …)
|
-


IV- Exercice :
Nébuleuse M57.
1)- Énoncé.
À l’exception du Soleil et de la Lune tous les astres du ciel
étoilé nous apparaissent ponctuels.
Certains observatoires astronomiques possèdent des lunettes très performantes
qui permettent de révéler les secrets des étoiles.
DOC.1 Caractéristiques de
la nébuleuse M57
La Nébuleuse de la Lyre (en anglais Ring Nebula), nommé dans le catalogue de
Messier sous le nom de M57, est une nébuleuse planétaire située dans la
constellation de la Lyre.
Sa forme caractéristique lui vaut également le surnom de Nébuleuse de
l'Anneau dont le diamètre est de 1,3 × 1013 km.
Elle a environ 10000 ans et se situe à environ 2600 années-lumière de la
Terre.
D’après Wikipédia.
DOC. 2 : Observatoire de
Harvard.
L’observatoire du Harvard Collège, aux États-Unis, s'est doté en 1847 d'une
lunette astronomique dont l'objectif a un diamètre de 38 cm et une distance
focale f’1= 6,80 m.
Il s'agissait d’un instrument remarquable pour l'époque au point de rester
célèbre sous le nom de « Grand réfracteur ».
Cet instrument a permis de nombreuses découvertes dont la première
photographique de l'étoile Véga et de la constellation de la Lyre en 1850.
D’après Astronomie, éditions Atlas.
DONNÉES :
-
Pouvoir séparateur de l’œil :
l’œil voit comme un point tout objet dont le diamètre est inférieur à ε = 3,0 × 10-4
rad.
-
Une année de lumière : 1 a.l = 1,0
× 1013 km.
Questions
1.
Question préliminaire :
-
Représenter sur un schéma, sans
souci d'échelle, le faisceau de lumière issu d'un point objet de la nébuleuse
M57 traversant une lunette à focale.
2.
Problème :
-
Déterminer si la nébuleuse M57
est observable autrement que sous forme ponctuelle à travers la lunette
astronomique de Harvard avec un oculaire de distance focale f’2
= 4,0 cm.

2)- Correction.
1.
Question préliminaire :
-
Schéma, sans souci d'échelle, de
la situation :
-
Faisceau de lumière issu d'un
point objet de la nébuleuse M57 traversant une lunette à focale.
-
Pour réaliser le schéma, on trace
un rayon qui fait un angle θ (quelques degrés) avec l’axe optique et qui
passe par le centre optique O1. Ce rayon n’est pas dévié.
-
On peut ainsi repérer le point
image B1 : point du rayon situé dans le plan focal image.
-
Pour obtenir le faisceau, on trace
les rayons parallèles au premier rayon tracé qui viennent sur les bords de
l’objectif. Ils émergent de l’objectif et convergent vers le point image B1.
-
Puis, on trace le rayon issu du
point B1 et qui passe par le centre optique O2.
-
Ce rayon n’est pas dévié.
-
Les autres rayons qui émergent de
l’oculaire sont parallèles à ce rayon.
-
On peut observer cette image qui
est située à l’infini.

►
Lunette astronomique afocale :
-
Une lunette est afocale lorsque le
foyer principal image de l’objectif coïncide avec le foyer principal objet de
l’oculaire.
-
Dans le cas présent : le foyer
principal image F’1 de l’objectif coïncide avec le le foyer
principal objet F2 de l’oculaire.
-
L’image, donnée par l’objectif de
la nébuleuse M57, est située dans le plan focal image.
2.
Problème :
-
Observation de la nébuleuse M57
à travers la lunette astronomique de Harvard.
-
Objectif de distance focale : f’1=
6,80 m
-
Oculaire de distance focale : f’2
= 4,0 cm
-
Nébuleuse de l'Anneau dont le
diamètre : D = 1,3 × 1013 km.
-
Distance M57-Terre : d
= 2600 a.l
-
Le but est de savoir si la
nébuleuse M57 est observable autrement que sous forme ponctuelle à
travers la lunette astronomique de Harvard avec un oculaire de distance focale
f’2 = 4,0 cm.
-
Il faut connaître la valeur de
l’angle θ’ sous lequel est vue l’image de la nébuleuse M57 à
travers la lunette astronomique de Harvard.
-
À partir des données, on détermine
la valeur de l’angle θ :
-
Dans le cas présent, on peut faire
l’approximation des petits angles en rad.
-
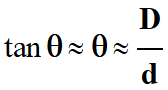
-
Le grossissement
G d’une lunette est donné par la
relation suivante :
|

|
|
G
|
Grossissement : nombre sans unité
|
|
θ’
|
L’angle θ’ sous lequel l'image est vue à travers la lunette
|
|
θ
|
L’angle θ
sous lequel l’objet est vu à l’œil nu
|
|
Il faut
exprimer θ’ et θ dans la même unité d’angle (° ou rad)
|
►
Cas d’une lentille afocale :
-
Grossissement d’une lentille
afocale :
|

|
|
G
|
Grossissement : nombre sans unité
|
|
f’1
|
Distance
focale de l’objectif
|
|
f’2
|
Distance
focale de l’oculaire.
|
|
Il faut
exprimer f’1 et f’2 dans la même
unité (m, cm, mm, …)
|
-
Résolution :
-

-

-
Application numérique :
-

-
En conséquence : θ’ > ε
= 3,0 × 10-4 rad
-
La nébuleuse M57 n’apparaît
pas comme ponctuelle lorsqu’on l’observe avec la lunette astronomique afocale de
Harvard.

V-
Exercice :
Les taches solaires.
1)- Énoncé.
Les taches solaires sont des régions de la surface du Soleil
qui intriguent les astronomes.
L’observation du Soleil est dangereuse puisqu'elle provoque la brûlure de la
rétine et peut conduire à la cécité.
Pour étudier les taches solaires les astronomes projettent l'image du soleil
sur un écran.
DOC. 1 : Les taches
solaires



Celestia
Stellarium

Wikipédia
Une tache solaire (anglais : sunspot) est une région sur la surface du Soleil
(photosphère) qui est marquée par une température inférieure à son environnement
et à une activité magnétique.
C’est son champ magnétique qui inhibe la convection par un effet similaire
aux freins à courants de Foucault, ralentissant ainsi l'apport de chaleur venant
de l'intérieur du Soleil (dans cette zone) formant des zones où la température
de surface est réduite.
C’est essentiellement la baisse de température de la tache relative à son
environnement qui la rend visible, l'émission de la tache étant de ce fait moins
intense.
D’après Wikipédia.
DOC. 2 : Lunette
astronomique équipée d’un écran.
Caractéristiques de la lunette astronomique :
-
Objectif convergent de diamètre
d = 70 mm et de distance focale f’1 = 900 mm
-
Oculaire de distance focale f’2
= 20 mm
Un écran peut être ajouté à la lunette à une distance
D = 32 cm de l'oculaire.

DOC. 3 : Diamètre apparent
du Soleil
a)-
La Lune peut être cachée par une pièce de 2 centimes d'euro placée à
2,0 m de l'observateur.


b)-
Éclipse de Soleil : la Lune cache le Soleil.
-
Diamètre du Soleil : dS
= 1,39 × 106 km

Problème
1.
Déterminer les modifications à apporter à une lunette astronomique
afocale afin de former l'image du Soleil sur un écran.
2.
Les taches solaires mesurant 5,0 mm de diamètre sur l'écran, estimer
le diamètre des taches solaires à la surface du soleil.

2)- Correction.
1.
Image du Soleil sur un écran
avec une lunette astronomique afocale.
-
Lunette afocale :
►
Lunette astronomique afocale :
-
Une lunette est afocale lorsque le
foyer principal image de l’objectif coïncide avec le foyer principal objet de
l’oculaire.
-
Dans le cas présent : le foyer
principal image F’1 de l’objectif coïncide avec le foyer
principal objet F2 de l’oculaire.
-
L’image A’B’, donnée
par l’objectif du Soleil, est située dans le plan focal image.
-
Schéma de la situation :

-
But recherché :
-
On veut régler la lunette
astronomique de telle sorte que l’image A’B’ du Soleil soit
obtenue sur un écran situé à la distance D = 32 cm.
-
On peut considérer que le Soleil
est situé à l’infini.
-
Il découle de ceci que l’image
A1B1 du Soleil est situé dans le plan image de
l’objectif qui contient le foyer image F’1.
-
Pour que l’image définitive se
forme sur un écran, il faut modifier la distance entre l’objectif et l’oculaire.
-
On veut une image réelle.
►
Construction
d’une image réelle :
-
Dans le cas d’une lentille
convergente, l’objet doit se trouver avant le foyer objet de la lentille
convergente.
-
O2A1
> f’2
-
Exemple :
-
Données : Diamètre de la
lentille : 6,0 cm
-
Distance focale : f’2
= 20 mm
-
L’objet est perpendiculaire à
l’axe optique.
-
Construction sans souci d’échelle.
-
On choisit :
-
Objet A1B1
= 1,0 cm
-
L’objet A1B1
est situé avant le foyer-objet à 1,5 cm du foyer-objet.
-
Réaliser la construction en
utilisant la méthode suivante :
-
Rayon 1 :
issu du point B1 passant par l’axe optique : il n’est pas
dévié.
-
Rayon 2 :
issu du point B1 et ce rayon est parallèle à l’axe optique. Il
émerge de la lentille en passant par le point F’2 foyer -
image.
-
Rayon 3 : issu du point B et passant par F2
(foyer - objet). Il émerge de la lentille parallèlement à l’axe optique.
- Schéma :

-
Il faut éloigner l’oculaire de l’objectif.
-
Schéma de la situation sans souci
d’échelle :
-
On éloigne l’oculaire de
l’objectif de la distance
ℓ.

-
Repère associé à un lentille mince
convergente :
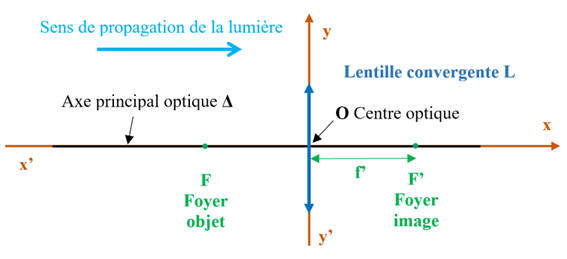
-
Relation de conjugaison appliquée
à la lentille L2 (oculaire) :
-

-
Le but est de trouver la valeur de

-
On
connaît :
 et
et

-
Résolution :
-

-
En réduisant :
-

-
Application numérique :
-

-
Il faut éloigner l’oculaire de
ℓ ≈ 0,10 cm de l’objectif :
-
La distance entre l’oculaire et
l’objectif : doboc
-
doboc = f’1
+ f’2 + ℓ
-
doboc
≈ 900 + 20 + 1,0
-
doboc
≈ 921 mm
2.
Diamètre des taches solaires à la surface du soleil.
-
Diamètre des taches solaires sur
l'écran : dtS = 5,0 mm.
-
Diamètre du Soleil : dS
= 1,39 × 106 km
-
Distance Terre-Soleil : dTerre-Soleil
-
Il faut connaître le diamètre D’
de l’image du Soleil donnée par la lunette astronomique sur l’écran.
-
L’angle θ représente le
diamètre apparent du Soleil.
-

-
D’autre part :
-

-
On en déduit la relation
suivante :
-

-
Pour la détermination de la
grandeur de l’image définitive, on peut utiliser la relation donnant le
grandissement de l’oculaire :
-
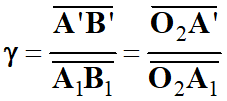
-
On peut travailler avec les
valeurs absolues
-

-
On peut considérer que A’B’
représente le diamètre D’ de l’image du Soleil donnée par la lunette
astronomique sur l’écran.
-
Or A1B1
représente le diamètre de l’image intermédiaire du Soleil.
-
 et
et
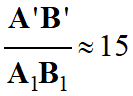
-

►
Une Méthode : On utilise les
données du DOC. 3 :
-
Diamètre apparent du Soleil :
-
L’exploitation du
DOC. 3 permet de
connaître la valeur du diamètre apparent θ du Soleil et par conséquence
de déterminer la valeur de la distance dTerre-Soleil.
-
Les éclipses de Soleil par la Lune
permettent de déduire que le diamètre apparent du Soleil est égal au diamètre
apparent de la Lune pour un observateur terrestre.
-
De même le diamètre apparent d’une
pièce de 2 centimes d’euro situé à 2,0 m de l’œil d’un observateur terrestre est
le même que celui de la Lune. Le diamètre apparent θ du Soleil est le
même que celui de la Lune pour un observateur terrestre
-
Exploitation du schéma :

-
On peut faire l’approximation des
petits angles exprimés en rad.
-

-

-
Application numérique :
-

-
Taille de l’image du Soleil sur
l’écran :
-

-
On peut considérer que A’B’
représente le diamètre D’ de l’image du Soleil donnée par la lunette
astronomique sur l’écran :
-
D’ ≈
1,3 × 102 mm
►
Remarque : On peut ne pas faire
les calculs intermédiaires :
-
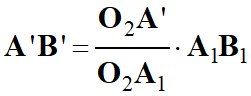
-
Et

-
 avec
avec

-
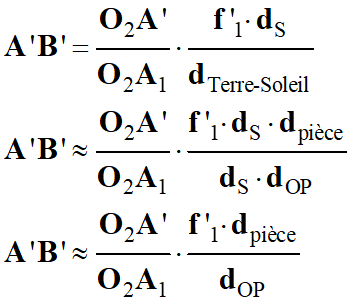
-
Applications numériques :
-

-
O2A’
= 32 cm
-
f’1
= 900 mm
-
dpièce
= 18,75 mm
-
dOP
= 2,0 m
-

-
On trouve pratiquement la même valeur pour
l’image A’B’
-
D'une part, l'image, supposée
circulaire, d'une des taches solaires a un diamètre dtS = 5,0
mm et l'image du Soleil a un diamètre D' ≈ 1,3 × 102 mm.
-
Diamètre réel DTS de
la tache solaire :
-
Tableau de valeurs :
|
|
Image
|
Réel
|
|
Soleil
|
1,3 × 102
mm
|
dS
= 1,39 × 106 km
|
|
Tache
|
5,0 mm
|
DTS
|
-

Taches solaires