|
Préparation
à l’ECE : Réalisation d’une lunette astronomique :
-
1.
Lentille utilisée pour l’objectif :
-
L’objet (immeuble) étant très loin, on
peut considérer qu’il est situé à l’infini.
-
L’image de cet objet se forme dans le
plan focal image de la lentille mince convergente considérée.
-
Schéma :

►
Plan focal :
-
Le plan focal image de la lentille
L1 est le plan
perpendiculaire à l’axe optique au foyer image
F’1 de la lentille
L1.
- Pour la lentille L1,
la distance focale est f’1
= d1 = 50,0 cm.
-
Pour la lentille
L2, la distance focale est
f’2 = d2
= 12,5 cm.
-
L’objectif d’une lunette astronomique
est constitué de la lentille mince convergente de plus grande distance
focale.
-
Dans le cas présent, la lentille
L1 de distance
focale f’1 = 50,0
cm.
2.
Distance O1O2
imposée afin de réaliser une lunette astronomique afocale :
►
Une lunette est afocale lorsque le foyer
principal image de l’objectif coïncide avec le foyer principal objet de
l’oculaire.
-
Schéma :

-
O1O2
= f’1 + f’2
-
O1O2
= 50,0 cm + 12,5 cm
-
O1O2
= 62,5 cm
3.
Protocole pour vérifier que l’image
intermédiaire A1B1 est réelle et
renversée par rapport à l’objet AB.

-
On recherche avec l’écran la position de
l’image d’un objet suffisamment éloigné pour être considéré comme étant
à l’infini.
-
Ainsi le faisceau de rayons parallèles
provenant de l’objet B situé
à l’infini émerge de la lentille
L1
en convergeant au point image
B1 situé dans le
plan focal image perpendiculaire à l’axe optique en
F’1.
-
Il faut déplacer l’écran entre
l’objectif et l’oculaire.
-
L’image obtenue est plus proche de
l’oculaire que de l’objectif.
-
L’image
A1B1
est réelle et renversée.
4.
Grossissement G de la lunette
astronomique afocale :
-
Le grossissement d’une lunette est le
rapport entre :
-
L’angle
θ sous lequel l’objet est vu
à l’œil nu et
-
L’angle
θ’ son image est vu à travers
la lunette.
-
Ainsi l’objet éloigné (B ∞) est vu sous l’angle
θ
et l’image A’B’ est vu sous l’angle
θ’.
-
Le grossissement
G d’une lunette est donné par la relation suivante :
 |
|
G
|
Grossissement : nombre sans unité
|
|
θ’
|
L’angle
θ’ son image est vu à travers la lunette
|
|
θ
|
L’angle
θ sous lequel l’objet est vu à l’œil nu
|
|
Il faut
exprimer θ’ et θ dans la même unité d’angle (°
ou rad)
|
-
Schéma :

-
Étude de la lunette afocale :
-
Le point
A1
est l’image du point A (situé
à l’infini) donnée par l’objectif de la lunette.
-
Le point
A1
est confondu avec le foyer image
F’1 de l’objectif et le foyer objet
F2 de l’oculaire.
-
L’image
A1B1 de
l’objet AB est
perpendiculaire à l’axe optique Δ.
-
Considérons le triangle
O1A1B1 rectangle en
A1 :
-

-
Considérons le triangle O2A1B1 rectangle en A1 :
-

-
Les angles
θ et
θ’ étants petits (en radian),
on peut faire l’approximation des petits angles :
-
Il faut exprimer
θ et θ’ en radian :
-
tan
θ ≈
θ et tan θ’ ≈
θ’
-
Dans ce cas :
-

-
On en déduit la relation suivante pour
une lunette afocale :
-

-
Grossissement d’une lentille afocale :
|
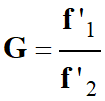
|
|
G
|
Grossissement : nombre sans unité
|
|
f’1
|
Distance
focale de l’objectif
|
|
f’2
|
Distance
focale de l’oculaire.
|
|
Il faut
exprimer f’1 et f’2 dans
la même unité (m, cm, mm, …)
|
-
Application numérique :
-
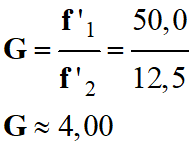
|