Calculer un angle caractéristique :

En éclairant une ouverture de diamètre d = 30 μm à l’aide d’une radiation de longueur d’onde λ = 532 nm,

on obtient sur un écran une figure de diffraction.

1.  Schématiser le dispositif expérimental.

2.  Calculer l’angle caractéristique de diffraction θ.

-  Donnée :

-   

Calculer un angle caractéristique :

1.  Schéma du dispositif expérimental.

-  Figure de diffraction :

-  Dans le cas d’une ouverture circulaire, la figure de diffraction obtenue a la symétrie de révolution :

-  Elle se compose d’anneaux alternativement sombres et brillants, entourant une tache centrale beaucoup plus brillante, qui porte le nom de tâche d’Airy.

-  Les limites angulaires de la tache d’Airy sont données par :

-   

-  λ : longueur d’onde dans le vide de la radiation lumineuse.

-  d : diamètre du trou.

-  La luminosité des anneaux brillants diminue au fur et à mesure que l’on s’éloigne de la tâche centrale.

-  Ce phénomène se produit lorsque l’ouverture par laquelle la lumière passe est de petite taille et du même ordre de grandeur que la longueur d’onde de la radiation.

-  L’ouverture a diffracté la lumière du laser.

2.  Angle caractéristique de diffraction θ.

-  

-  Application numérique :

-   

Reconnaître des ondes :

Deux vibreurs frappent la surface de l’eau d’une cuve à ondes et donnent naissance à des interférences.

On place deux flotteurs en (A) et (B) sur ce plan d’eau.

ou

Interférences à deux ondes (animation)

1.  À quelle condition peut-on observer le phénomène d’interférences ?

2.  On représente ci-dessous la hauteur d’eau sous les flotteurs en fonction du temps.

Attribuer, à chaque flotteur (A) et (B), la courbe (a) ou (b) qui lui correspond.

Reconnaître des ondes :

1.  Observation du phénomène d’interférences :

-  Condition :

-  Pour obtenir des interférences, les sources doivent être cohérentes et de même nature.

-  Elles doivent être de même fréquence (synchrones) et présenter un déphasage constant.

-  Les sources, qui émettent ces ondes, sont des sources ponctuelles en phase.

-  Dans le cas de la cuve à ondes, les deux vibreurs sont reliés à la même tige pour vibrer de la même façon (à la même fréquence et en phase).

2.  Attribution, à chaque flotteur (A) et (B), la courbe (a) ou (b) qui lui correspond.

-  La figure d’interférences est composée d’une alternance de zones colorées en bleu clair et d’autre en bleu foncé.

-  L’amplitude est maximale pour les zones colorées en bleu foncé.

-  L’amplitude est minimale pour les zones colorées en bleu clair.

-  Flotteur (A) :

-   ou

-   

-  Le flotteur (A) est situé à l’intersection de deux franges foncées.

-  L’élongation est maximale et l’interférence est constructive.

-  Cette situation correspond à la courbe (a).

►  Flotteur (B)

-    (pas trop visible)

-   

-  Le flotteur (B) est situé à l’intersection d’une frange sombre et d’une frange claire.

-  L'élongation est minimale et l’interférence est destructive.

-  Cette situation correspond à la courbe (b).

Connaître le phénomène d’interférences :

1.  Quelle(s) condition(s) doivent remplir des sources lumineuses pour qu’il y ait des interférences ?

2.  Quelle condition la différence de chemin optique entre les deux ondes doit-elle respecter pour observer :

a.  Des interférences constructives ?

b.  Des interférences destructives ?

On réalise, dans l’air, une expérience d’interférences avec un système de deux fentes d’Young

éclairées par une radiation de longueur d’onde λ₀ = 650 nm.

On observe une figure d’interférences sur un écran.

1.  Qu’observe-t-on sur l’écran au point O ?

2.  Les ondes arrivent au point P avec une différence de chemin optique ΔL = 1,625 μm.

Qu’observe-t-on au point P ?

Identifier une expression :

Au point P d’abscisse x_k de l’exercice 14, la différence de chemin optique ΔL est :

-   

1.  Exprimer x_k en fonction de ΔL, b et D.

2.  En déduire l’interfrange i.

Identifier une expression :

-  Schéma de la situation :

-  Radiation de longueur d’onde λ₀ = 650 nm 

1.  Expression de x_k en fonction de ΔL, b et D.

-   

2.  Valeur de l’interfrange i.

-  Lors d’interférences lumineuses, l’interfrange, notée i, est la distance séparant

deux franges brillantes consécutives ou deux franges sombres consécutives.

-  i = x_k+1 –x_k

-  Prenons le cas de deux franges sombres consécutives :

-  Niveau k :

-   

-  Niveau k+1 :

-  

- Interfrange i :

-   

-  On se place dans le cas suivant :

-  Deux fentes étroites et parallèles, séparées par une distance b = 0,200 mm,

-   L’écran est placé à la distance D = 1,00 m du plan de ces fentes.

-  Application numérique :

-   

Calculer une longueur d’onde :

On réalise une figure d’interférences lumineuses à l’aide de fentes d’Young séparées par une distance b = 0,20 mm.

La figure est obtenue sur un écran situé à D = 2,0 m.

Dans une telle situation, la valeur de l’interfrange i est donnée par la relation suivante :

-   

1.  Donner l’expression de la longueur d’onde en fonction de l’interfrange i, de b et de D.

2.  Calculer la longueur d’onde de la lumière utilisée sachant que, dans les conditions de l’expérience, on mesure i = 6,3 mm.

Calculer une longueur d’onde :

-  Schéma de la situation :

1.  Expression de la longueur d’onde λ en fonction de l’interfrange i, de b et de D.

-   

2.  Valeur de la longueur d’onde de la lumière utilisée.

-  Dans les conditions de l’expérience,

-  i = 6,3 mm

-  b = 0,20 mm,

-   D = 2,0 m

-  Application numérique :

-   

-  La valeur de la longueur d’onde utilisée est voisine de 630 nm.

-  Radiation rouge-orangé :

Pointeur laser :

On dispose d’un pointeur laser émettant dans l’air, des radiations rouges de longueur d’onde λ_R.

On souhaite vérifier expérimentalement la longueur d’onde λ_R.

Pour cela, on réalise un montage permettant d’obtenir une figure de diffraction, à travers une ouverture circulaire de rayon r = 0,20 mm,

sur un écran placé à une distance D = 5,0 m.

La figure obtenue est la suivante.

1.  Schématiser le montage du dispositif expérimental.

2.  En utilisant le schéma, exprimer la longueur d’onde λ_R en fonction de la distance D, du rayon r de l’ouverture et de la largeur ℓ de la tache centrale.

3.  Calculer la longueur d’onde des radiations émises par la diode laser du pointeur rouge.

4.  Dans les mêmes conditions, on utilise un laser émettant, dans l’air, des radiations de longueur d’onde λ_V = 405 nm.

Comment la largeur de la tache centrale évolue-t-elle ?

-  Donnée :

-  L’angle θ étant petit en radian, on a tan θ ≈ θ.

Pointeur laser :

1.  Schéma du montage du dispositif expérimental.

-  Schéma de la situation :

2.  Expression de la longueur d’onde λ_R en fonction de la distance D, du rayon r de l’ouverture et de la largeur ℓ de la tache centrale.

-  Pour les ondes lumineuses, dans le cas d’une ouverture circulaire de diamètre d et de rapport  petit :

-   

-  Dans le cas présent :

-   

-  D’autre part :

- 

-  Or l’angle θ est petit en radian car D >> ℓ ,

-  On peut faire l’approximation suivante :

-  tan θ ≈ θ

-   

3.  Longueur d’onde λ_R des radiations émises par la diode laser du pointeur rouge.

-  Exploitation de la figure de diffraction :

-  ℓ ≈ 2,1 cm

-  Application numérique :

-   

-  La valeur de la longueur d’onde du pointeur laser est voisine de 690 nm.

-   

4.  Évolution de la largeur de la tache centrale lors du passage de λ_R à λ_V.

 -  Dans les mêmes conditions, on utilise un laser émettant, dans l’air, des radiations de longueur d’onde λ_V = 405 nm.

-  λ_{V <} λ_R

-  Comme la largeur de la tache centrale est donnée par la relation suivante :

-   

-  λ_{V <} λ_R => ℓ_{V <} ℓ_R

-  La largeur de la tache centrale est plus petite.

-  On peut faire le calcul :

-   

-  Couleur de la radiation : radiation violette.

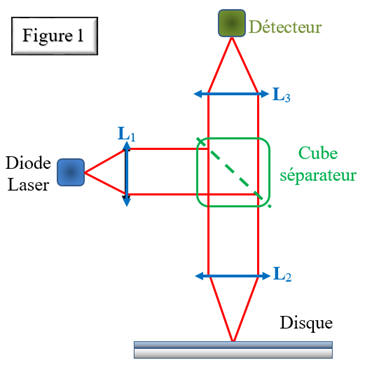
Lecteur de disque optique Blu-ray :

Sur un disque optique (CD, DVD, Blu-ray), les données sont gravées sous forme de minuscules cavités,

de longueur variable, appelées « creux ». Les espaces entre les creux sont appelés « plats ».

C’est la variation d’intensité lumineuse au cours de la lecture qui permet de repérer les creux et les plats,et de décoder l’information numérique.

Afin de lire les données du disque, un faisceau laser est dirigé vers le disque optique.

Le faisceau se propage dans du polycarbonate puis se réfléchit et est renvoyé vers un capteur de lumière qui détecte l’intensité lumineuse réfléchie.

Les diodes lasers utilisées dans les lecteurs Blu-ray émettent une lumière de longueur d’onde dans le vide λ₀ = 405 nm.

A.  Lecture des données sur le disque optique.

a.  Le faisceau laser se réfléchit totalement sur un plat :

b.  Le faisceau laser est positionné en face d’un creux : le rayon (1) situé au bord du faisceau se réfléchit sur un plat,

tandis que le rayon (2) situé au centre du faisceau se réfléchit sur un creux.

1.  À quelle condition des interférences sont-elles constructives ? destructives ?

2.   

a.  Dans le cas (a), les interférences entre les rayons (1) et (2) sont-elles constructives ? destructives ?

b.  Dans le cas (b), la différence de chemin optique ΔL entre les rayons (1) et (2) est ΔL = 2 n × h.

Que représente h ? Calculer sa valeur minimale pour que les interférences soient destructives.

-  Donnée :

-  Indice de réfraction du polycarbonate : n = 1,55