|
|
Diffraction et interférences |
|
|
|
|
|
1)- Conditions d’observation et
caractéristiques. a)-
Cas des ondes mécaniques : mise en évidence du phénomène : c)-
En résumé : le phénomène de diffraction. |
|
III- Les interférences de deux ondes lumineuses monochromatiques. |
|
QCM r
Diffraction Interférences Les interférences de deux ondes lumineuses monochromatiques
|
|
Exercices : énoncé avec correction
1)- Exercice 07
page 378 : Calculer un angle caractéristique. 2)- Exercice 11
page 379 : Reconnaître des ondes. 3)- Exercice 13
page 379 : Connaître le phénomène d’interférences. 4)- Exercice 14
page 379 : Déterminer la position d’une frange. 5)- Exercice 15
page 379 : Identifier une expression. 6)- Exercice 17
page 380 : Calculer une longueur d’onde. 7)- Exercice 21
page 381 : Pointeur laser. 8)- Exercice 28
page 383 : Lecteur de disque optique Blu-ray. 9)- DS N° 01 :
Observation d’une exoplanète (20 min) : Exercice 29 page 384. 10)- DS N° 02 :
Les fentes de Young (30 min : Exercice 30 page 385. 11)- Préparation à
ECE : Phénomène créé par une fente étroite. |
|
QCM r Diffraction Interférences Les interférences de deux ondes lumineuses monochromatiques
|
1)- Conditions d’observation et caractéristiques.
a)-
Cas des ondes mécaniques :
mise en évidence du phénomène :
►
Expérience :
-
On produit des ondes
rectilignes grâce à la cuve à onde et on observe ce qui se passe lorsque ces
ondes rectilignes rencontrent une ouverture.
-
Lorsque l’ouverture
est grande, les ondes rectilignes sont peu affectées lors du passage de
celle-ci.

-
Lorsque l’ouverture
devient plus petite, on observe une modification de l’onde rectiligne après le
passage de l’ouverture.


-
On passe d’une onde
rectiligne à une onde circulaire. L’onde perd de sa directivité
-
On a mis en évidence
le phénomène de diffraction.
-
Ce phénomène est
caractéristique des ondes.
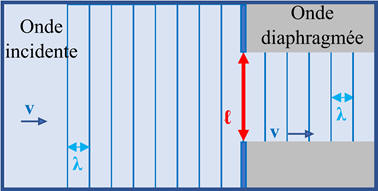
-
L’onde qui arrive sur l’ouverture est
appelée, onde incidente et l’onde après l’ouverture est appelée onde diffractée.
-
Au cours du phénomène
de diffraction, l’onde perd sa directivité.
►
Expérience :
►
Observations :
-
Lorsque la fente est
large, environ 2 mm, le faisceau laser n’est pratiquement pas modifié.
-
On diminue la largeur
de la fente.
-
Lorsque la largeur de
la fente est inférieure à 1 mm, on observe sur l’écran un étalement du faisceau
laser perpendiculairement à la fente.
-
Cet étalement de la
lumière est appelé figure de diffraction.
-
Elle est constituée
d’une tache centrale et de taches secondaires situées symétriquement par rapport
à la tache centrale.
-
La tache centrale est
très lumineuse et deux fois plus large que les autres taches.
-
La luminosité diminue
très vite lorsqu’on s’éloigne de la tache centrale de diffraction.
-
La fente a diffracté
la lumière dans une direction perpendiculaire à celle de la fente.
- La diffraction est d’autant plus marquée que la largeur de la fente est petite.
c)-
En résumé : le phénomène de
diffraction.
|
-
Le phénomène de
diffraction, changement de direction de propagation d’une onde, |
-
L’onde diffractée a
même fréquence et même longueur d’onde que l’onde incidente (dans le cas d’un
milieu homogène).
-
Pour une longueur
d’onde donnée, le phénomène de diffraction est d’autant plus marqué que la
dimension de l’ouverture ou de l’obstacle est plus petite.
d)-
Angle
caractéristique de diffraction
θ.
►
Figure de diffraction
d’une onde mécanique et angle caractéristique
θ :

-
L’importance du
phénomène peut être mesurée à l’aide de l’angle caractéristique de diffraction
θ.
►
Figure de diffraction
d’ondes lumineuse monochromatique : Écart
angulaire θ :
-
L’écart angulaire est
l’angle sous lequel est vue la moitié de la tache centrale depuis l’objet
diffractant.
-
C’est le demi-diamètre
angulaire de la tache centrale.
-
Schéma :

-
F :
milieu de la fente.
-
O :
milieu de la tache centrale.
-
M :
milieu de la première extinction.
-
L :
largeur de la tache centrale de diffraction.
-
D
>> L :
D est très
grand devant OM.
|
Lorsqu’un faisceau parallèle de lumière de longueur d’onde λ traverse une fente de largeur a,
l’écart angulaire θ,
entre le centre de la tache centrale et la première extinction est donné par la
relation suivante : |
|
|
|
|
θ |
Écart angulaire en radian (rad) |
|
λ |
Longueur d’onde en mètre (m) |
|
a |
Largeur de l’ouverture rectangulaire |
-
Si le rapport
![]() est
petit, on peut faire l’approximation suivante :
est
petit, on peut faire l’approximation suivante :
-
sin
θ
≈ θ
(rad) :
-
la relation s’écrit
alors :
|
|
|
|
θ |
Écart angulaire en radian (rad) |
|
λ |
Longueur d’onde en mètre (m) |
|
a |
Largeur de l’ouverture rectangulaire |
-
Cette relation permet
de déterminer expérimentalement la longueur d’onde
λ de la lumière
d’un faisceau connaissant la largeur de la fente.
-
Dans le cas ou
D >> L
(largeur de la
tache centrale), on peut
déterminer la relation donnant la largeur de la tache centrale
L
en fonction de la longueur d’onde λ
et de la largeur a
de la fente.
-
On fait
l’approximation des petits angles.
-

►
Cas d’une ouverture
circulaire :

- Figure de diffraction :

-
Dans le cas d’une ouverture
circulaire, la figure de diffraction obtenue a la symétrie de
révolution :
-
Elle se compose d’anneaux
alternativement sombres et brillants, entourant une tache centrale
beaucoup plus brillante, qui porte le nom de tâche d’Airy.
-
La luminosité des anneaux brillants
diminue au fur et à mesure que l’on s’éloigne de la tâche centrale.
-
Ce phénomène se produit lorsque
l’ouverture par laquelle la lumière passe est de petite taille
et du
même ordre de grandeur que la longueur d’onde de la radiation.
-
L’ouverture a diffracté la lumière du
laser.
-
Pour
les ondes lumineuses, dans le cas d’une ouverture circulaire de diamètre
d
et de rapport
![]() petit :
petit :
-
![]()
2)- Situations de diffraction.
-
Le phénomène de
diffraction peut s’observer aussi bien avec les ondes électromagnétiques qu’avec
les ondes mécaniques.
-
C’est grâce au
phénomène de diffraction que l’on a mis en évidence le caractère ondulatoire de
la lumière.
-
Le phénomène de
diffraction intervient dans de nombreuses situations physiques :
-
La lecture optique ;
-
La cristallographie ;
-
L’astronomie ;
-
L’acoustique …
►
Les disques optiques
du commerce :
|
Format |
CD |
DVD |
BD |
|
Longueur d’onde
(nm) |
780 |
650 |
405 |
|
Ouverture
numérique NA |
0,45 |
0,60 |
0,85 |
|
Écartement des
lignes (μm) |
1,6 |
0,74 |
0,32 |
|
Taille minimale
d’un creux (nm) |
126 |
105 |
65,3 |
|
Capacité de
stockage (Gio) |
0,75 |
4,4 |
23 |
-
Les disques Blu-ray
(BD) concurrencent les disques CD et DVD car leur capacité de stockage est plus
importante.
-
Schématisation de la
surface de trois types de disques optiques.
►
Augmentation de la
capacité de stockage :
-
Schéma du dispositif :
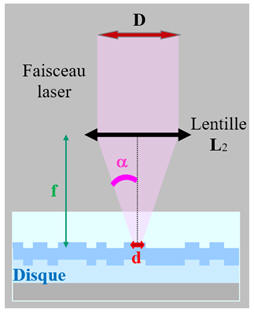
-
D
est le diamètre du faisceau laser.
-
d
est le diamètre du spot sur le disque,
-
f
est la distance focale de la lentille convergente,
-
a est l'angle du cône lumineux
émergent de la lentille.
-
Le diamètre
d du spot du
faisceau laser dépend de la longueur d’onde λ
de la radiation et de l’ouverture numérique (NA)
qui dépend de l’émetteur laser.
►
L’ouverture
numérique :
-
L’ouverture numérique (NA : Numerical Aperture) est
définie par la relation suivante :
-

►
Le diamètre du spot
laser
-
Du fait du phénomène
de diffraction, le spot du laser ne sera pas ponctuel mais aura la forme d'un
disque de diamètre d.
|
Le diamètre d du spot laser sur le disque optique est proportionnel à la longueur d’onde λ de la radiation
et inversement proportionnel à l’ouverture numérique,
NA, qui dépend de
l’émetteur laser.
|
►
Augmentation de la
densité de données sur un disque :
-
Pour augmenter la
capacité de stockage, il faut allonger la longueur de la piste.
-
Cela revient à
resserrer la spirale si l’on veut garder la même taille du disque.
-
Il faut diminuer la
largeur des creux et des plats.
-
Pour une lecture
correcte, le spot du faisceau laser doit être le plus étroit possibles pour ne
pas intercepter deux lignes contigües de creux et de plats.
-
La diminution de la
longueur d’onde λ
de la radiation et l’augmentation de l’ouverture numérique
NA de l’émetteur
laser permettent de diminuer le diamètre du spot laser.
-
Mais, le phénomène de
diffraction impose, pour une radiation de longueur d’onde donnée, un diamètre
minimal du faisceau.
-
La capacité de
stockage des disques optiques est donc limitée.
-
On peut calculer le
diamètre d
du spot du faisceau laser correspondant à chaque format.
|
Format |
CD |
DVD |
BD |
|
Longueur d’onde
λ (nm) |
780 |
650 |
405 |
|
Ouverture
numérique NA |
0,45 |
0,60 |
0,85 |
|
Taille minimale
d’un creux (nm) |
126 |
105 |
65,3 |
|
Capacité de
stockage (Gio) |
0,75 |
4,4 |
23 |
|
Écartement des
lignes (μm) |
1,6 |
0,74 |
0,32 |
|
Diamètre
d du spot laser (μm) |
2,1 |
1,3 |
0,58 |
►
Exemple cas du CD :
-
L’écartement des
lignes est e
= 1,6 μm et le diamètre du spot laser est d
= 2,1 μm
-
Bien que
e <
d, le faisceau
laser étant centré sur une ligne, il n’éclaire pas les autres lignes situées à
côté.
-
Schéma de la
situation :
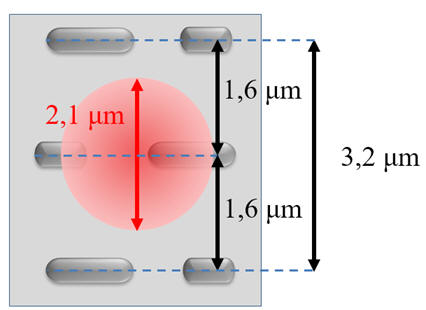
Dans cette situation,
le faisceau n’éclaire qu’une ligne à la fois.
►
En Astronomie :
-
La monture des
objectifs diffracte la lumière reçue ;
-
Pour une bonne
résolution, il faut augmenter leur diamètre.
►
Principe de la cuve à
ondes :
-
Une cuve à onde permet
de visualiser la propagation d’ondes progressives à la surface d’un liquide
(l’eau).

Une source crée une vibration (une pointe dans le cas
présent).
-
Le système est éclairé
par une lampe à lumière stroboscopique.
-
On ajuste la fréquence
de la lumière à celle de l’onde.
-
La lumière traverse la
surface du liquide et se réfléchit sur un miroir qui projette l’image sur un
écran dépoli.
-
Les vibrations
périodiques de la pointe S créent des ondes circulaires périodiques et
concentriques qui se propagent à la surface de l’eau
-
L’état vibratoire d’un
point de la surface de l’eau est appelé phase.
►
Expérience avec une
pointe :

-
Les zones sombres de
l’image correspondent aux crêtes de l’onde (traits pleins)
-
Les zones
brillantes
de l’image correspondent aux creux de l’onde (pointillés).
-
Schéma : Vue de
profil et vue de dessus

►
Expérience avec deux
pointes :
-
Une fourche munie de
deux pointes est fixée à l’extrémité d’un vibreur.
-
Les
pointes S1
et S2
ont ainsi la même fréquence et constituent deux sources cohérentes.
-
Elles font naître à la
surface de l’eau des ondes circulaires.
-
Il en résulte la
propagation de deux ondes progressives circulaires qui se superposent.
-
On obtient une figure
d’interférences.
-
Photos du phénomène :


-
Lorsque les deux ondes
interfèrent, les signaux correspondant à chacune des ondes s’additionnent.
-
Les zones sombres de
l’image correspondent aux crêtes (traits pleins)
-
Les zones brillantes
de l’image correspondent aux creux (pointillés).
-
Schéma :

-
L’état d’un point
donné dépend de l’état vibratoire de chaque onde en ce point.
-
C’est le phénomène
d’interférences à deux ondes.
-
On distingue deux
situations remarquables :
-
Les
ondes sont en opposition de phase (intersection d’un trait plein et d’un
pointillé) : on dit que l’interférence est
destructive :
-
Schéma :

https://physique-chimie.ac-normandie.fr/spip.php?article173

-
La
courbe rouge
représente les variations de l’onde
issue de S1
au cours du temps.
-
La
courbe bleue
représente les variations
de l’onde issue de
S2 au cours du temps.
-
La
courbe jaune
représente les variations de la
superposition des deux ondes au point
M.
-
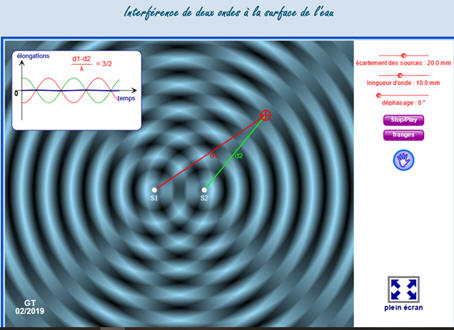
Les
ondes sont en phase (intersection de deux traits pleins ou de deux pointillés) :
on dit que l’interférence est
constructive.
-
Schéma :
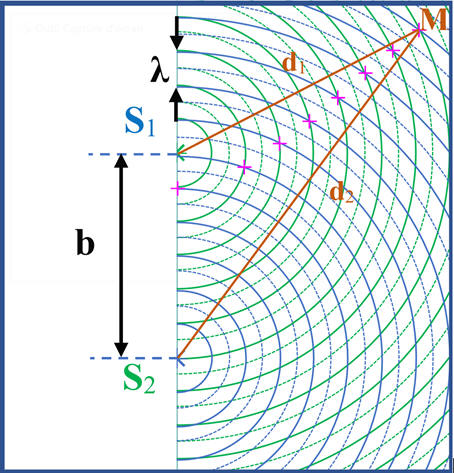
https://physique-chimie.ac-normandie.fr/spip.php?article173

-
Pour
obtenir des interférences, les sources doivent être
cohérentes
et de même nature.
-
Elles doivent être de
même fréquence (synchrones) et présenter un déphasage constant.
-
Les sources, qui
émettent ces ondes, sont des sources ponctuelles en phase.
3)- Interférences constructives et destructives.
-
À la surface de l’eau,
les interférences constructives correspondent à la superposition de deux ondes
en phase, c’est-à-dire d’élongations toutes les deux extrémales (maximales ou
minimales).
-
Lorsque deux ondes
interfèrent, les signaux correspondant à chacune des ondes s’additionnent.
-
En un
point M,
-
il y a
interférences
constructives si l’amplitude
du signal résultant en ce point est
maximale.
-
Il y a
interférences
destructives si l’amplitude
du signal résultant en ce point est
minimale.
►
Différence de distance
et différence de marche :
-
Schéma
de la situation : Au point
M :
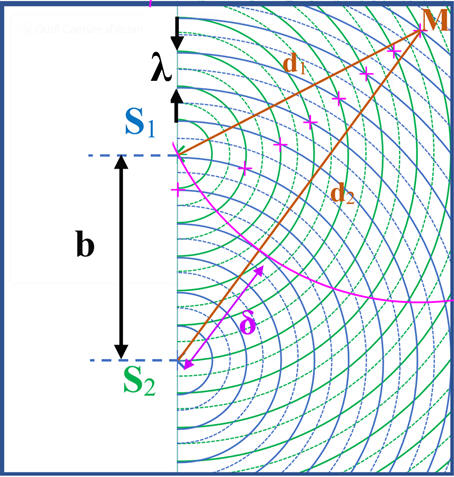
-
Pour
arriver au point M, les ondes issues de
S1
et S2
ne parcourent pas la même distance :
-
La différence de
distance se note :
-
δ
= d2
– d1
-
On
l’appelle aussi différence de marche.
-
Si
δ
= k
. λ,
-
Les
deux ondes arrivent au point
M en phase et elles ajoutent leurs
effets.
-
L’interférence est constructive.
►
Remarque :
-
La
courbe rouge
n’apparaît pas car elle se situe au-dessous de
la
courbe bleue.
-
Les deux courbes ont
la même amplitude, la même période.
-
La
courbe bleue
cache la
courbe rouge.
-
Schéma
de la situation au point
M’ :
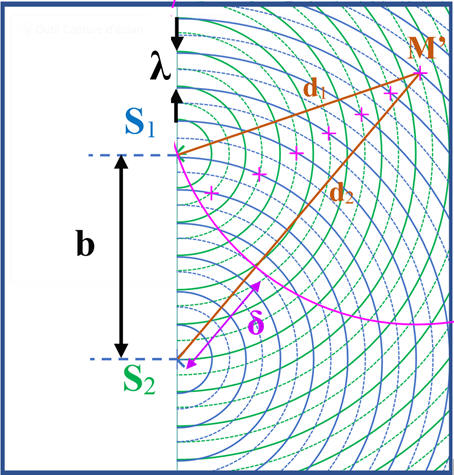
-
Si,
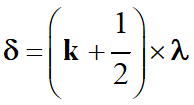
-
Les deux ondes
arrivent au point M’
en opposition de phase et elles annulent leurs effets.
-
L’interférence est destructive.

►
Remarque :
-
On remarque bien que
les courbes
rouge
et
bleue
sont en opposition de phase.
-
Quand l’une est
maximale, l’autre est minimale et inversement.
4)- Cas de deux signaux sinusoïdaux :
-
Un
signal sinusoïdal est caractérisé par sa période
T,
son amplitude A
et sa phase à l’origine
φ.
-
On peut donner
l’expression de ce signal sous la forme suivante :
-

-
Considérons que S1
et S2
soient deux sources synchrones en phase qui émettent des ondes de même nature
dans un milieu homogène.

-
Expression du signal au point
M atteint par l’onde issue de
S1
à l’instant t :
-
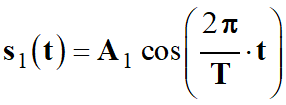
-
Expression du signal au point
M atteint par l’onde issue de
S2
à l’instant t :
- 
-
La
grandeur τ
représente le retard pris par l’onde issue de
S2
par rapport à celle issue de S1
du fait de la différence de distances
δ
(différence de marche) parcourues par les deux ondes pour atteindre le point
M.
-
Au
point M,
on observe la superposition de deux signaux sinusoïdaux :
-

►
Si
δ =
k .
λ :
-
On
note : c la célérité de l’onde,
λ
sa longueur d’onde,
T sa période.
-
La
grandeur τ
représente le retard pris par l’onde issue de
S2
par rapport à celle issue de S1.
-
C’est
la durée du parcours de
δ.
-

-
Signal
résultant au point M :
-
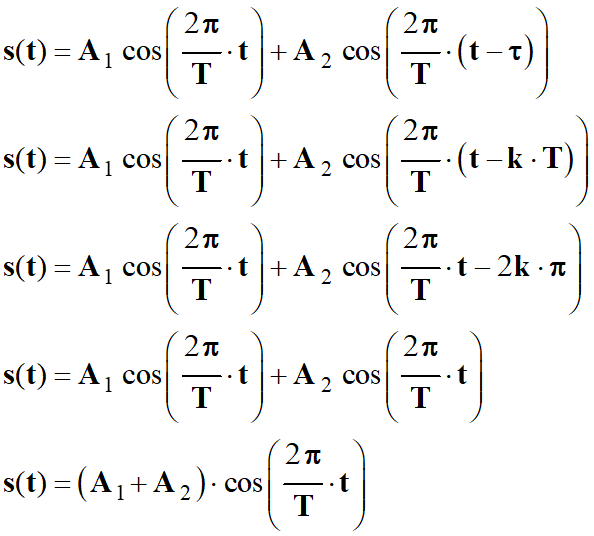
-
Les deux signaux sont
en phase et ajoutent leurs effets :
►
Si 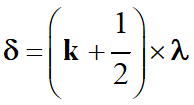
-
Dans ce cas :
-
Signal
résultant au point M :
-

-
Les deux signaux
arrivent au point M
en opposition de phase et elles annulent leurs effets.
-
On peut faire la
simulation avec le tableur Excel :
-
On a mis des
amplitudes différentes pour les deux ondes pour que le phénomène de
superposition des deux ondes soit plus visible.
-
Il ne faut pas oublier
qu’il y a un amortissement des deux ondes lors de leur déplacement.
-
L’amortissement est
plus grand pour celle qui parcourt la plus grande distance.
|
k
= 0 |
|
k
= ½ |
|
k
= 1 |
|
k
= 1 + ½ |
III-
Les interférences de deux
ondes lumineuses monochromatiques.
|
|
|
La tache centrale de diffraction est striée de fines bandes rectilignes rouges, parallèles, équidistantes.
|
-
Pour observer une
figure d’interférences avec de la lumière, il faut éclairer les deux fentes avec
une unique source de lumière monochromatique.
-
Dans le
cas présent, on utilise la lumière rouge de longueur d’onde dans le vide
λ0
= 632,8 nm émise par un laser (laser hélium-néon :
He–Ne).
-
Le laser émet une
lumière cohérente et monochromatique.
-
Au phénomène de
diffraction se superpose le phénomène d’interférence.
-
Les deux fentes
étroites se comportent comme des sources lumineuses synchrones et en phase.
-
L’ensemble des franges
alternativement brillantes (rouges) et sombres constitue des franges
d’interférences.
-
Elles sont parallèles
entre elles et parallèles aux deux fentes d’Young
-
La distance entre deux
franges sombres ou brillantes (rouges) est la même.
-
On l’appelle
l’interfrange, noté i.
2)- Différence de chemin optique.
-
Schéma de la
situation :
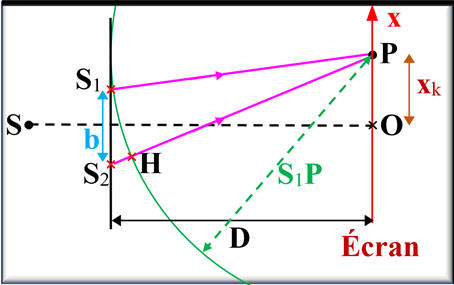
-
Les
deux ondes lumineuses de longueur d’onde
λ0
= 632,8 nm émises par les sources secondaires
S1
et S2
se superposent au point
P de l’écran.
-
L’onde
lumineuse, issue de S1,
a parcourue la distance S1P.
-
L’onde
lumineuse, issue de S2,
a parcourue la distance S2P.
-
Les deux ondes ne
parcourent pas la même distance :
-
La différence de
distances :
-
S2H
= S2P
– S1P
-
On
l’appelle aussi la différence de marche :
-
δ
= S2H =
S2P
– S1P
►
Différence de marche
et différence de chemin optique :
-
On
définit le chemin optique
L comme le produit de l’indice
n
de réfraction du milieu de propagation par la distance
e
parcourue par le rayon lumineux dans le milieu :
-
L
= n
. e
-
Le
chemin optique pour l’onde lumineuse issue de
S1
:
-
L1
= n .
S1P
-
Le
chemin optique pour l’onde lumineuse issue de
S2
:
-
L2
= n .
S2P
-
La
différence de chemin optique
ΔL entre les deux ondes est donnée par
la relation :
-
ΔL
= n
. δ =
n
. S2H =
n
. (S2P –
S1P)
►
Interférences
constructives et destructives :
-
Interférences constructives :
-
Si
ΔL
= k
. λ0
avec k
€ ℤ
-
Les
ondes arrivent en phase au point
P.
-
Les interférences sont
constructives.
-
On observe une frange
brillante.
-
Interférences destructives :
-
Si
 avec
k
€ ℤ
avec
k
€ ℤ
-
Les
ondes arrivent en opposition de phase au point
P.
-
Les interférences sont
destructives.
-
On observe une frange
sombre.
►
Remarque :
-
La
longueur d’onde λ d’une radiation lumineuse
dépend du milieu de propagation.
-
Alors
que la période T et de ce fait la fréquence
f
ne dépendent pas du milieu de propagation :
-
Une
onde de longueur d’onde λ0
dans le vide a une longueur d’onde
![]() dans
un milieu d’indice n.
dans
un milieu d’indice n.
-
Dans le cas où les
ondes lumineuses se déplacent dans l’air :
-
On fait
intervenir l’indice de réfraction de l’air :
n
= 1,00
-
Dans ce cas, on peut
écrire :
-
ΔL
= n
. δ =
n
. S2H =
n
. (S2P –
S1P)
-
ΔL
= δ
= S2H
= (S2P –
S1P)
-
Lors
d’interférences lumineuses, l’interfrange, notée
i,
est la distance séparant deux franges brillantes consécutives ou deux franges
sombres consécutives.
-
i
= xk+1
–xk
-
Schéma de la
situation :


-
Différence de chemin
optique :
-
ΔL
= n
. δ =
n
. S2H =
n
. (S2P –
S1P)
-
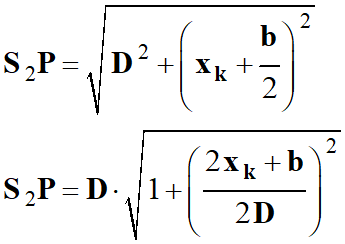
-

-
Étude de l’expression
suivante :
-
On se
place dans le cas ou :
D >>
b et
D
>> xk
-
L’expression
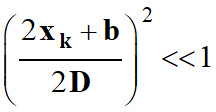 :
:
-
On pose : 
-
La
grandeur ε
est une grandeur qui est petite devant 1 :
-
On utilise
l’approximation suivante :
-
![]()
-
On applique cette
approximation à l’expression suivante :
-

-
En
appliquant le même principe à l’expression de
S1P, on obtient :
-

-
Or :
-
ΔL
= n
. δ =
n
. S2H =
n
. (S2P –
S1P)
-
Dans le
cas ou D >>
b,
l’expression de la différence de chemin optique est donnée par la relation :
- 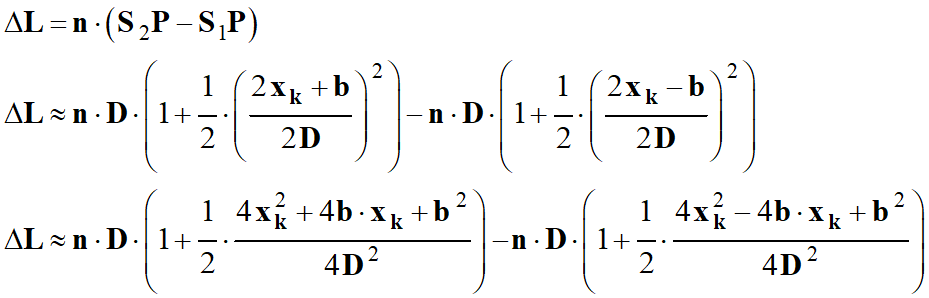
-
En réduisant, on
obtient :
-

-
En conclusion :
-
La
différence de chemin optique
ΔLk au
point P
d’abscisse xk
est donnée par expression suivante :
-
![]()
-
Expression de
l’interfrange :
-
i
= xk+1
–xk
-
Prenons le cas de deux
franges brillantes consécutives :
-
ΔLk
= n
. k
. λ0
et ![]()
-
ΔLk+1
= n
. (k +
1) .
λ0 et
![]()
-
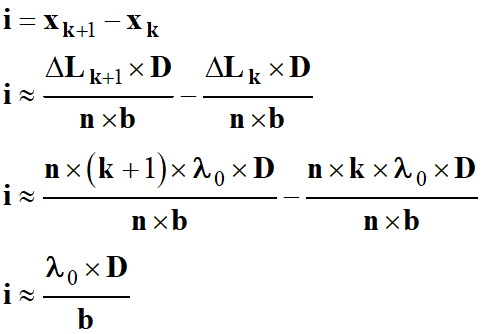
-
L’interfrange i est donnée par la relation
suivante :
|
|
|
|
i |
Interfrange en
mètre (m) |
|
λ0 |
Longueur
d’onde de la radiation dans le vide en mètre (m) |
|
D |
Distance des
sources lumineuses à l’écran en mètre (m) |
|
b |
Distance entre
les deux sources lumineuses en mètre (m) |
-
Schéma :


1)- Diffraction et interférences :
-
Détermination du
diamètre d’un cheveu :
-
Étude de la
diffraction :
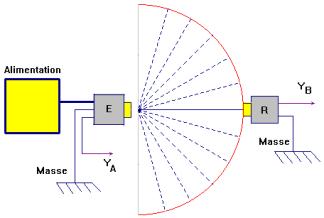
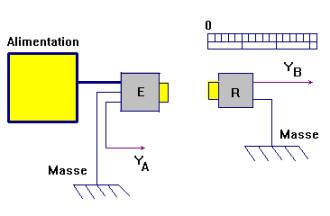
|
QCM r Diffraction et Interférences Les interférences de deux ondes lumineuses monochromatiques
|
|
Exercices : énoncé avec correction
Préparation à l'ECE. 1)- Exercice 07
page 378 : Calculer un angle caractéristique. 2)- Exercice 11
page 379 : Reconnaître des ondes. 3)- Exercice 13
page 379 : Connaître le phénomène d’interférences. 4)- Exercice 14
page 379 : Déterminer la position d’une frange. 5)- Exercice 15
page 379 : Identifier une expression. 6)- Exercice 17
page 380 : Calculer une longueur d’onde. 7)- Exercice 21
page 381 : Pointeur laser. 8)- Exercice 28
page 383 : Lecteur de disque optique Blu-ray. 9)- DS N° 01 :
Observation d’une exoplanète (20 min) : Exercice 29 page 384. 10)- DS N° 02 :
Les fentes de Young (30 min : Exercice 30 page 385. 11)- Préparation à
ECE : Phénomène créé par une fente étroite. |
|
|