|
Phénomène créé
par une fente étroite :
1.
Nom du phénomène observé :
-
On observe sur l’écran un étalement du faisceau laser
perpendiculairement à la fente.
-
Cet étalement de la lumière est appelé figure de diffraction.
-
Elle est constituée d’une tache centrale et de taches secondaires
situées symétriquement par rapport à la tache centrale.
-
La tache centrale est très lumineuse et deux fois plus large que les
autres taches.
-
La luminosité diminue très vite lorsqu’on s’éloigne de la tache centrale
de diffraction.
-
La fente a diffracté la lumière dans une direction perpendiculaire à
celle de la fente.
-
Schéma de la situation :



2.
Relation donnant la longueur d’onde :
-
Schéma :

-
Données :
-
La longueur d’onde : 630 nm ≤
λ
≤ 650 nm
-
Largeur de la première fente utilisée :
a
= (60,0 ± 0,1) μm.
-
Distance fente-écran :
D
= (2,0 ± 0,1) m.
-
Largeur de la tache centrale :
ℓ
= (4,2 ± 0,1) cm
-
Lorsqu’un faisceau parallèle de lumière de longueur d’onde λ
traverse une fente de largeur a,
l’écart angulaire θ,
entre le centre de la tache centrale et la première extinction
est donné par la relation suivante :
|
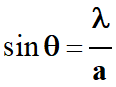
|
|
θ
|
Écart
angulaire en radian (rad)
|
|
λ
|
Longueur
d’onde en mètre (m)
|
|
a
|
Largeur
de l’ouverture rectangulaire en mètre (m)
|
-
Si le rapport
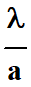 est petit, on peut
faire l’approximation suivante : est petit, on peut
faire l’approximation suivante :
-
sin θ
≈ θ
(rad) :
-
On peut donner une estimation de la valeur du rapport sachant que : 630
nm ≤
λ ≤ 650 nm
-

-
Si on calcule :
-
sin (1,08 × 10–2) ≈ 1,08331 × 10–2
-
On remarque que l’approximation est excellente.
-
La relation s’écrit alors :
|
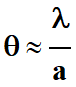
|
|
θ
|
Écart
angulaire en radian (rad)
|
|
λ
|
Longueur
d’onde en mètre (m)
|
|
a
|
Largeur
de l’ouverture rectangulaire en mètre (m)
|
-
Cette relation permet de déterminer expérimentalement la longueur d’onde
λ de la lumière d’un faisceau connaissant la largeur de la fente.
-
D’autre part :
-
Distance fente-écran :
D
= (2,0 ± 0,1) m.
-
Largeur de la tache centrale :
ℓ
= (4,2 ± 0,1) cm
-
Dans le cas ou D >> ℓ (largeur de la tache centrale), on peut déterminer la relation
donnant la largeur de la tache centrale
ℓ
en fonction de la longueur d’onde λ et de la largeur
a de la fente.
-
On fait l’approximation des petits angles.
-
L’angle θ étant petit,
-
tan θ ≈ θ avec θ en radian (rad) :
-

-
On retrouve bien la relation donnée dans l’énoncé.
-

3.
a.
Longueur d’onde λ de la radiation :
-
Longueur d’onde de la radiation :
-

-
Incertitude-type à partir des
mesures expérimentales :
-
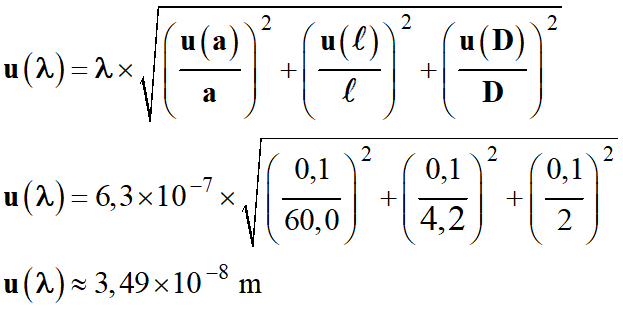
-
On arrondit par excès l’incertitude-type :
-
u
(λ) = 0,4 × 10–7 m
b.
Encadrement de la valeur expérimentale de la
longueur d’onde λ.
-
λ
= (6,3 ± 04) × 10–7 m
c.
Conclusion en comparant la valeur trouvée à
celle donnée par le constructeur.
-
Encadrement donnée par le constructeur :
6,30 × 10–7 m ≤ λ ≤ 6,30 × 10–7
m
-
Encadrement de la valeur expérimentale :
5,9 × 10–7 m ≤ λ ≤ 6,7 × 10–7
m

-
L’encadrement expérimental est compatible avec l’encadrement
constructeur.
-
L’encadrement constructeur est inclus dans l’encadrement expérimental.
4.
Influence de la largeur de la fente sur la tache
centrale.
-
L’élève utilise une fente de largeur différente (b) de celle
étudiée précédemment (a).
|
(a)
|

|
|
(b)
|

|
-
La tache centrale de diffraction de l’expérience
(b)
est moins large que la tache de diffraction de l’expérience
(a).
-
Lors des expériences, seule la largeur
a
de la fente change.
-
Or :
-
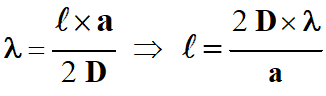
-
Comme ℓ
diminue, alors la largeur
a
de la fente augmente (la grandeur
a
intervient au dénominateur de l’expression).
-
L’élève a utilisé une fente plus large lors de l’expérience
(b).
|