I- Le Transfert thermique.

1)- Introduction.

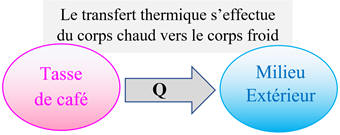
-  Un transfert thermique s’effectue entre un système S et le milieu extérieur ( ME ) lorsqu’il existe une différence de température entre eux.

-  On considère le régime de transfert comme permanent et indépendant du temps.

►  Transfert thermique spontané :

-  Cas d’une tasse de café  (65 ° C) qu’on laisse à la température ambiante (21 ° C).

-  Au cours du temps, la température de la tasse de café diminue.

-  La tasse de café constitue le système d’étude S , l’autre système ( ME )  est constitué par le milieu extérieur.

-  Un transfert d’énergie s’effectue de la tasse de café vers le milieu extérieur ( ME ).

-  La tasse de café cède de l’énergie sous forme de transfert thermique, notée Q, au milieu extérieur.

-  Un transfert thermique a pour conséquence macroscopique une modification de la température T (ou θ ) ou un changement d’état physique du système.

2)- Les modes de transfert thermique.

Transferts d'énergie et énergie interne

Transferts d'énergie et conservation

a)-  Introduction :

-  Au niveau macroscopique, la température et l’état physique d’un corps peuvent être modifiés par transfert thermique Q.

-  Au niveau microscopique, le transfert thermique Q s’effectue par chocs entre les particules de manière désordonnée.

-  Les particules les plus agitées transmettent leur énergie cinétique aux particules les moins agitées.

-  Il existe trois types de transfert thermique :

-  La conduction thermique, la convection thermique et le rayonnemen t thermique.

b)-  La conduction thermique :

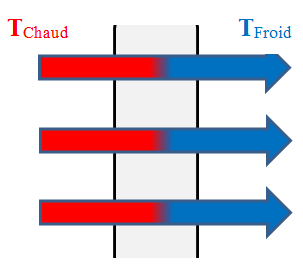
-  Si l'on chauffe l'extrémité d'une barre métallique, on remarque que la température de l'autre extrémité augmente très vite.

-  Les particules de la partie chaude communiquent une partie de l'agitation thermique aux particules voisines et ainsi de suite.

-  L'agitation thermique se transmet de proche en proche de la région chaude vers la région froide sans transport de matière.

-  La conduction se produit principalement dans les solides

c)-  La convection thermique :

-  Dans les fluides, le transfert de chaleur se fait grâce aux courants de convection.

-  Exemple :

-  L'air chaud est plus léger que l'air froid.

-  L'air chaud s'élève et en s'élevant, se refroidit en échangeant de l'énergie avec les couches supérieures.

-  L’agitation thermique se transmet de proche en proche dans le fluide avec déplacement d’ensemble de celui-ci : des courants de fluide circulent.

https://upload.wikimedia.org/wikipedia/commons/0/08/Convection.gif

-  La convection se produit principalement dans les fluides (liquides et gaz).

d)-  Le rayonnement thermique :

-  L'énergie transportée sous forme de radiations électromagnétiques est appelée énergie rayonnante .

-  Elle est notée W_R. Elle s'exprime en joule (J).

-  Tout corps chaud émet des radiations électromagnétiques qui transportent de l'énergie.

-  Le rayonnement ne nécessite pas de milieu matériel, il s’effectue même dans le vide.

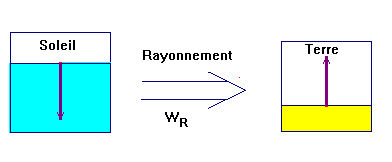
-  Le rayonnement thermique se produit dans tout milieu et même dans le vide.

-  L’absorption et l’émission d’ondes électromagnétiques par la matière en modifient l’agitation thermique.

3)- Le flux thermique et la résistance thermique.

• Flux et résistance thermique

a)-  Définition du flux thermique :

-  Le flux thermique Φ (phi majuscule) caractérise la vitesse du transfert thermique Q pendant une durée Δt au sein d’un système ou entre différents systèmes.

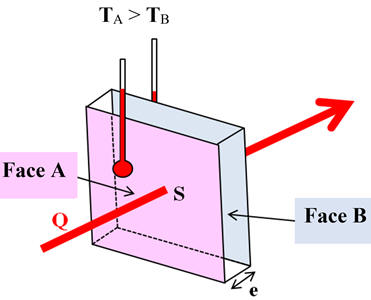
-  On considère un matériau dont les deux faces parallèles numérotées 1 et 2, de même surface S, sont à des températures différentes T₁ et T₂ , telles que T₁ > T₂.

-  La paroi plane, dont deux faces sont à des températures différentes T₁ et T₂ , est le siège d’un transfert thermique par conduction.

-  La capacité d’un matériau, à réaliser plus ou moins rapidement ce transfert, est liée à sa résistance thermique R_th.

-  L’énergie Q est transférée de la face 1 vers la face 2 pendant la durée Δt.

-  Le flux thermique Φ (phi majuscule) traversant ce matériau est alors défini par la relation :

-  Le flux thermique a la dimension d’une puissance : c’est une énergie par unité de temps.

-  Le flux thermique est l’énergie transférée à travers une paroi par unité de temps.

-  Ce transfert se fait spontanément de la source chaude vers la source froide.

-  Ce transfert est naturellement irréversible.

-  Par convention, le flux thermique est compté :

-  Positivement s’il est reçu par le système S  ;

-  Négativement s’il est cédé par le système S.

-  Le flux thermique Φ (phi majuscule) est aussi appelé puissance thermique, notée _th.

-  Remarque :

-  Un flux thermique peut aussi s’exprimer par unité de surface.

-  On parle alors de flux thermique surfacique, noté φ (phi minuscule), en watt par mètre carré (W . m ^–2)

b)-  Résistance thermique :

-  La résistance thermique R _th caractérise l’opposition d’un milieu au transfert thermique entre deux points A et B.

-  On considère le système S de résistance thermique  R _th :

-  On oriente le flux thermique du point A vers le point B.

-  Si l’écart de température T_A – T_B est maintenu constant, le flux thermique Φ est donné par la relation suivante :

-  En quelle unité s’exprime la résistance thermique R _th  ?

-  La résistance thermique s’exprime en (K . W ^–1 ) ou (° C . W ^–1 ).

-  Remarque :

-  Plus la résistance thermique du matériau est élevée, plus le flux thermique est faible à travers le matériau.

-  Ce dernier empêche le transfert d’énergie à travers lui ; c’est de ce fait un bon isolant thermique.

-  Un matériau qui a une résistance thermique élevée est un bon isolant thermique.

c)-  Calculer et exploiter un flux thermique :

d)-  Résistance thermique R _th et conductivité thermique λ d’un matériau.

-  La résistance thermique R _th d’une paroi dépend :

-  De la conductivité thermique λ du matériau ;

-  De son épaisseur e ;

-  Et de la surface S traversée par le flux.

-  Elle est proportionnelle à l’épaisseur e et inversement proportionnelle à la conductivité thermique λ et à la surface S.

-  Relation :

-  La conductivité thermique caractérise un matériau :

►  Exemples :

►  Cas de plusieurs parois accolées :

-  Lorsque plusieurs parois sont accolées, la résistance thermique totale R _{th tot} est égale à la somme des résistances thermiques de chaque paroi.

-  Relation :

-   

-  Avec : R _{th tot} = R _th1 + R _th2 + R _th3 + R _th4 + …

II- La température terrestre moyenne.

1)- Introduction.

2)- Le corps noir :

-  Un corps noir est un objet théorique qui absorbe intégralement le rayonnement électromagnétique qu’il reçoit.

-  Sous l’effet de l’agitation thermique induite, ce corps émet alors un rayonnement électromagnétique qui ne dépend que de sa température.

-  La loi de Stefan-Boltzmann permet de relier cette température T (K) au flux thermique surfacique rayonné φ _E  ou à la puissance thermique surfacique p.

-  Remarque : p est comptée ici positivement.

-  En physique, un « corps noir » est un objet idéal émettant un rayonnement qui n’est fonction que de sa température.

Lumière émise par une source chaude

3)- L’Albédo :

-  L’Albédo est le pouvoir réfléchissant d’une surface.

-  L’albédo α est une grandeur sans unité qui caractérise l’aptitude d’une surface à renvoyer, par diffusion et / ou réflexion, le rayonnement qui lui parvient.

-  Sa valeur est comprise entre 0 et 1.

-  Considérons un système S qui reçoit un rayonnement électromagnétique bien déterminé :

-  On peut prendre comme exemple le rayonnement solaire.

-  Le système S reçoit le flux thermique surfacique φ_T ou p _T (puissance surfacique) reçu du Soleil ;

-  Une partie du rayonnement solaire reçu est réfléchi et / ou diffusé, φ _R  ou p _R par le système S

-  Schéma de la situation :

-  Relation :

-  Le flux thermique surfacique moyen émis par le Soleil et reçu par le système {Terre et atmosphère} est égal à : φ _T = 350 W . m ^–2

-  Les Albédos de différentes surfaces :

-  Le système {Terre et atmosphère} présente un albédo moyen de l’ordre de 0,3.

-  Ce nombre est considérable.

-  Les continents, le sable et la neige apportent une contribution très importante.

4)- Bilan quantitatif d’énergie du système {Terre et atmosphère}

-  Schéma :

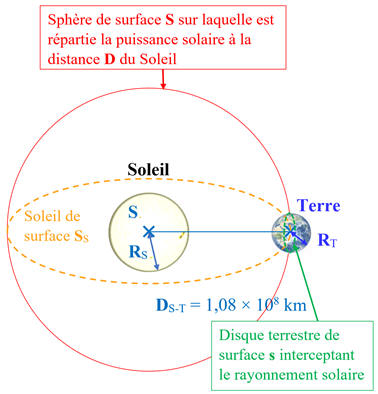
-  Le système étudié : {Terre et atmosphère}

-  Le Soleil et la Terre sont assimilés à des corps noirs.

-  Le Soleil et la Terre sont des systèmes incompressibles qui échangent de l’énergie par rayonnement, mais n’échangent pas de matière avec l’extérieur.

-  Référentiel d’étude : référentiel héliocentrique.

-  Dans ce référentiel :

-  On considère :

-  La distance Soleil-Terre : D _S-T = 1,08 × 10 ⁸ km = cte

-  La vitesse du système {Terre et atmosphère} est considérée comme constante.

-  Le système {Terre et atmosphère} n’échange aucune énergie par travail de force non conservative :

-  W = 0

-  En régime permanent indépendant du temps, le système {Terre et atmosphère} est à l’équilibre thermique car sa température est supposée constante :

-  En conséquence :

-  ΔU _i→f = 0 (quels que soient les états initial et final)

-  Notations  :

-  Transfert thermique reçu de la part du Soleil : Q _T

-  Transfert thermique renvoyé par le système {Terre et atmosphère} : Q _R

-  Transfert thermique émis par le système {Terre et atmosphère} : Q _E

5)- Application du 1 ^ier principe de la thermodynamique au système {Terre et atmosphère}

-  L’application du premier principe de la thermodynamique au système {Terre et atmosphère} permet d’écrire :

-  ΔU _i→f = Q _T + Q _R + Q _E et ΔU _i→f = 0

-  On en déduit la relation suivante :

-  Q _T + Q _R + Q _E = 0 (1)

-  En divisant l’expression (1) par la durée Δt  :

-  On fait intervenir les flux thermiques Φ (ou les puissances thermiques ) :

-   

-  Ou :

-  _T +_R +_E = 0

-  Schéma de la situation :

-  Remarque :

-  En divisant l’expression précédente par la surface du système, on fait intervenir le bilan des puissances thermiques surfaciques :

-  p_T + p_R + p_E = 0 (2)

-  Comme on considère que le système {Terre et atmosphère} se comporte comme un corps noir, on peut utiliser la loi de Stefan-Boltzmann :

-  –  p_E = σ . T_T⁴ car p_E < 0

-  La grandeur T_T représente la température moyenne de la Terre en kelvin (K) :

-   

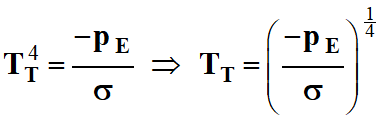
-  On peut exprimer la température moyenne de la Terre T_T en fonction de la puissance surfacique reçue de la part du Soleil p _T et la puissance surfacique renvoyée par le système {Terre et atmosphère} p_R  :

-  p_T + p_R + p_E = 0 (2)  =>  p_T + p_R = – p_E

-  On en déduit la relation suivante :

-   

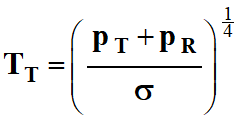
-  La température moyenne de la Terre est de 15 ° C.

►  L’Albédo et l’effet de serre.

-  L’albédo et l’effet de serre exercent une grande influence sur la température moyenne de la Terre

-  Tableau :

-  Une diminution de l’Albédo du système {Terre et atmosphère} entraîne une élévation de la température moyenne de la Terre.

-  Une augmentation de l’effet de serre entraîne une augmentation de la température terrestre moyenne.

-  Schéma :

III- La loi de Newton.

1)- Modèle de la loi de Newton.

a)-  Notion de transformation élémentaire.

►  La notation différentielle :

-  La notation dU désigne une différentielle totale exacte.

-  La grandeur dx représente un infiniment petit.

-  La grandeur df ( x ) représente une variation infinitésimale de la fonction f ( x ).

-  La notation δF représente une forme différentielle.

►  Notations en thermodynamique :

-  L’énergie interne U ( T , P , V ) est une fonction d’état.

-  Le travail W et le transfert thermique Q , échangés entre le système S et le milieu extérieur, ne peuvent pas être assimilés à la variation d’une fonction d’état.

-  Dans le cas général le travail W et le transfert thermique Q dépendent du chemin parcouru entre l’état initial et l’état final du système S.

-  La possibilité de représenter par exemple, le transfert thermique Q , par une fonction d’état est liée aux propriétés de sa forme différentielle,

   c’est-à-dire sa variation dans une transformation infinitésimale autour d’un état d’équilibre.

-  Si U est une fonction d'état, sa variation élémentaire entre deux états ne dépend que de l'état initial et de l'état final et non du chemin suivi.

-  On peut donc la calculer le long de n'importe quel chemin allant du départ à l'arrivée.

-  On note cette variation élémentaire dU.

-  dU est une différentielle totale exacte de la fonction d’état U.

-  En revanche, si Q est la somme des accroissements entre le départ et l'arrivée, et dépend du chemin suivi.

-  Alors, on note cette variation élémentaire δQ.

-  δQ est une forme différentielle

-  En thermodynamique, l’énergie interne U est une fonction d’état de différentielle dU.

-  L’énergie s’échangeant soit sous forme de travail ou / et sous forme de transfert thermique

-  δW et δQ sont des formes différentielles

-  Leur somme est une différentielle totale exacte.

►  Écriture différentielle du premier principe de la thermodynamique :

-  Variation infinitésimale de l’énergie interne d’un système S qui échange un travail δW et transfert thermique δQ  :

-  dU = δW + δQ

b)-  Réécriture des relations importantes :

c)-  Modèle de la loi de Newton

-  Le système S  :

-  Le système S est incompressible et il est en contact avec le milieu extérieur,

-  Mais il n’échange pas de matière avec le milieu extérieur.

-  Le but est de modéliser l’évolution de la température du système S.

-  Schéma :

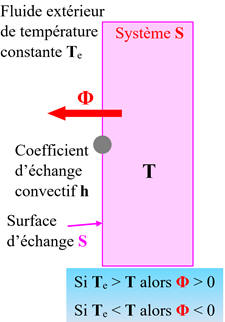
-  Considérons que le mode principal de transfert thermique est la convection dans le fluide.

-  Dans ce cas, on peut utiliser la loi de Newton :

-  Elle modélise le flux thermique convectif Φ à partir d’observations expérimentales :

-  Elle relie le flux thermique convectif Φ et la différence de température ( T_e – T ) :

-  Le système dont la surface d’échange S avec le milieu extérieur a pour température T supposée uniforme ;

-  Le milieu extérieur de température T_e constante, appelé thermostat :

-  Relation dans le cas envisagé :

-  Le coefficient d’échange convectif h, entre le système incompressible et le milieu extérieur, d’un des deux étant fluide, dépend de la nature du fluide.

2)- Bilan d’énergie d’un système incompressible.

-  Le système S  :

-  Il est incompressible et il est à la température θ  au temps t ;

-  Il échange de l’énergie par transfert thermique convectif avec le thermostat

-  Il est en contact avec le milieu extérieur, ou thermostat à la température constante θ _e.

-  L’un des deux est un fluide.

-  Le système S est au repos macroscopique.

-  Il n’échange pas de matière avec le milieu extérieur ou thermostat.

-  On note θ _i la température du système S à l’instant initial.

►  Application du premier principe de la thermodynamique au système S :

-  Il n’échange pas de travail W avec le milieu extérieur.

-  Il échange seulement de l’énergie Q par transfert thermique convectif avec le thermostat (milieu extérieur).

-  Entre l’état initial ( i ) et l’état final ( f ), on peut écrire :

-  ΔU _i→f = Q

-  Pour une durée suffisamment courte, on peut écrire :

-  Q = Φ . Δt

-  D’après la loi de Newton :

-  Φ = h . S . ( θ _e – θ)

-  Q = h . S . ( θ _e – θ ) . Δt

-  D’autre part, pour un système incompressible de masse m, de capacité thermique massique c dont la variation de température est Δθ :

-  Q = m . c . Δθ

-  On obtient la relation suivante :

-  ΔU _i→f = h . S . ( θ _e – θ ) . Δt = m . c . Δθ

-  On peut exprimer le rapport de l’écart de température Δθ sur la durée Δt :

-   

►  Établissement de l’équation différentielle :

-  Lorsque Δt → 0,

-  La limite de l’expression   est égale à la dérivée de θ par rapport au temps t  :

-  On écrit en utilisant la notation différentielle :

-  :

-  En développant, on obtient :

-   

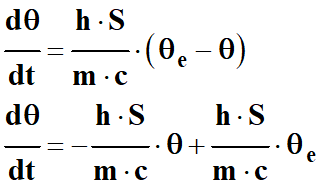
-  Et enfin :

-   

-  On est en présence d’une équation différentielle linéaire du premier ordre en θ à coefficients constants avec un deuxième membre constant.

-  On pose :

-   

-  Écriture de l’équation différentielle :

-  (1)

-  Elle admet une solution du type :

-   

-  A , B et k sont des constantes liées aux conditions initiales et aux caractéristiques du système.

►  Recherche des constantes :

-  La solution  vérifie l’équation différentielle (1)

-  Détermination de :

-   

-  On remplace  et θ par leur expression respective dans l’équation (1) :

-   

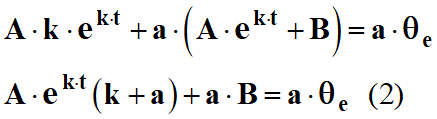
-  La relation (2) est vérifiée à chaque instant :

-  La grandeur ( a . θ _e ) est une constante,

-  La grandeur ( a . B) est une constante

-  Mais t et  varient au cours du temps.

-  Il faut nécessairement que :

-   

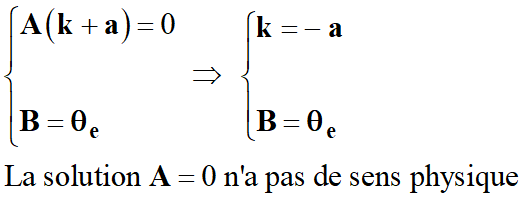
-  D’autre part, au temps t = 0 s, θ = θ _i

-  Comme

-   θ _i = A + B

-  A = θ _i – B

-  A = θ _i – θ _e

-  La solution :

-   

-  Avec :

-   

-  On pose :

-  Enfin :

-   

-  La grandeur τ est appelée grandeur caractéristique du système.

-  Elle s’exprime en seconde (s).

►  Allure de la courbe donnant la température d’un système en contact avec un thermostat en fonction du temps.

-  Premier cas : Refroidissement du système incompressible : θ _i > θ _e

-  Dans le cas présent : θ _i = 50 ° C et θ _e = 5,0 ° C

►  Détermination expérimentale de la constante de temps τ.

-  On trace la tangente à la courbe au point d'abscisse t = 0 s et l'asymptote horizontale

-  La constante de temps τ est donnée par l'abscisse de leur point d'intersection.

-  Détermination de :

-  Or :

-   

-  Dans le cas présent : θ _i = 50 ° C et θ _e = 5,0 ° C

-   

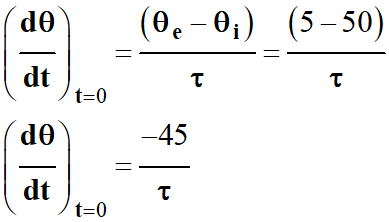
-  Par lecture graphique, on trouve :

-  τ ≈ 1,25 h

-  Second cas : Réchauffement du système incompressible : θ _i < θ _e

-  Dans le cas présent : θ _i = 5,0 ° C et θ _e = 50 ° C

►  Détermination expérimentale de la constante de temps τ.

-  Dans le cas présent : θ _i = 5,0 ° C et θ _e = 50 ° C

-   

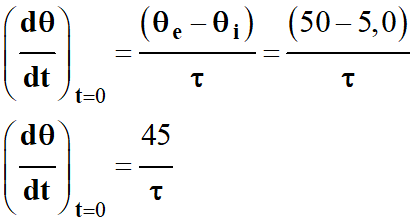
-  Par lecture graphique, on trouve :

-  τ ≈ 1,25 h

-  La grandeur τ est appelée temps caractéristique de l’évolution temporelle du système.

-  Dans le cas présent, on peut considérer qu’au bout de la durée de 5 τ , l’équilibre thermique est établi entre le système et le thermostat : θ ≈ θ _e

-   

-  Écriture de l’équation différentielle :

- 

-  Écriture de la solution :

-   

3)- Bilan énergétique d’un système incompressible : autre approche.

-  Le système S  :

-  Masse du système  : m

-  Capacité thermique massique du système : c

-  Coefficient d’échange convectif du système  : h

-  Surface d’échange du système : S

-  Il est incompressible et il est à la température θ  à l’instant t ;

-  Il échange de l’énergie par transfert thermique convectif avec le thermostat

-  Il est en contact avec le milieu extérieur, ou thermostat à la température constante θ _e.

-  L’un des deux est un fluide.

-  Le système S est au repos macroscopique.

-  Il n’échange pas de matière avec le milieu extérieur ou thermostat.

-  On note θ _i la température du système S à l’instant initial.

-  On veut connaître l’évolution de la température θ du système au cours du temps t.

-  Soit θ = f ( t)

-  Pour ce faire, on dispose :

-  Du premier principe de la thermodynamique

-  ΔU = W + Q

-  et

-  De la loi de Newton ( le système S échange de l’énergie par transfert thermique convectif avec le thermostat :

-  Φ = h . S . (θ _e – θ)

-  On considère une transformation élémentaire du durée dt pour le système S  :

-  Comme le système S est incompressible, au repos macroscopique et qu’il n’échange pas de matière avec le milieu extérieur :

-  Le premier principe de la thermodynamique permet d’écrire pour la transformation élémentaire :

-  dU = δW + δQ  avec δW = 0

-  dU = δQ (1)

-  Lors de cette transformation, la température θ du système S varie d’une valeur élémentaire dθ  :

-  dU = m . c . dθ (2)

-  Transfert thermique du système :

-  δQ = Φ . dt (3)

-  Il échange de l’énergie par transfert thermique convectif avec le thermostat qui est à la température θ_e :

-  Φ = h . S . (θ _e – θ) (4)

-  En combinant (1), (2), (3) et (4) :

-  m . c . dθ = h . S . (θ _e – θ) . dt

-   

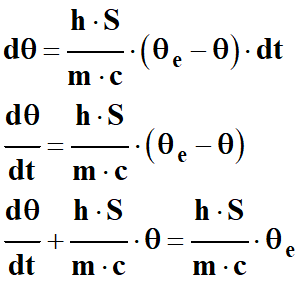
-  On pose :

-   

-  On obtient l’équation différentielle suivante :

-   

-  On est en présence d’une équation différentielle linéaire du premier ordre en θ à coefficients constants avec un deuxième membre constant.

-  Elle admet une solution du type :

- 

IV- Applications.

1)- QCM :

2)- Exercices :